统计岩体力学(SMRM)
——岩体工程地质力学的传承与发展*
伍法权 王思敬 潘别桐
(① 绍兴文理学院, 绍兴 312000, 中国) (② 中国科学院地质与地球物理研究所, 北京 100029, 中国) (③ 中国地质大学(武汉), 武汉 430074, 中国)
0 引 言
谷德振讲座是由中国科学院页岩气与地质工程重点实验室发起的中国工程地质高端学术讲座。讲座每年一届,旨在推进“工程地质力学创新与发展”,弘扬我国工程地质科学精神。本讲座已由重点实验室在京举办了四届(表 1),每届论坛一个主题,由一位主讲人和若干位知名工程地质学家共同完成。

表 1 历届谷德振讲座主题与主讲人Table 1 Topics and speakers of previous Gu Dezhen Lectures
2021年起,谷德振讲座转由中国地质学会工程地质专业委员会和重点实验室联合主办。经评审委员会批准,由华北水利电力大学承办第五届讲座,我本人有幸和陈剑平、兰恒星、单治钢、刘汉东、李广诚、胡新丽、李邵军、刘晓丽、范宣梅、陈永贵等同行应邀担任报告人。
本文是第五届谷德振讲座的主讲报告,简要回顾岩体工程地质力学的核心价值与历史贡献,并重点介绍统计岩体力学(Statistic Mechanics of Rock Masses,简称SMRM)的理论与技术探索及其对岩体工程地质力学的传承与发展。
1 岩体工程地质力学的历史贡献
岩体工程地质力学是20世纪70年代由谷德振先生等中国工程地质先驱们创立的独特的中国工程地质科学体系。在中华人民共和国成立后的二、三十年中,我国工程地质学家在水利水电、铁路、公路和建筑工程等领域进行了广泛的实践,先后出版了《水利水电工程地质》、《实用铁路工程地质》等阶段性总结成果。1979年科学出版社出版了《岩体工程地质力学基础》,标志着岩体工程地质力学思想体系的建立。几十年来,王思敬、孙广忠、孙玉科、许兵、黄鼎成、李毓瑞等,以及我国新一代的工程地质学家对岩体工程地质力学的丰富和发展做出了重要贡献。
岩体工程地质力学不仅是我国独特的工程地质学科理论,也在支撑我国几十年来大规模工程建设、指导我国岩体工程技术规范体系建设、高等专业教育和工程地质人才队伍培养方面做出了不可磨灭的历史贡献。
1.1 岩体工程地质力学的思想体系与核心价值
岩体工程地质力学根本改变了之前人们对研究客体的认知及其行为规律的探索思路。它以岩体地质结构及其力学效应为基础,以人类活动与地质环境相互作用为灵魂,形成了一套全新的科学思想体系。岩体工程地质力学的思想体系与核心价值集中体现在:
(1)对岩体特性认知的革命。在20世纪60年代的经典岩石力学时代,提出岩体结构这一命题是一场革命,它改变了传统的连续介质思维模式,使人们不得不首先考虑岩体结构的作用。岩体结构概念强调,不同成因的岩体具有不同的结构特征,块状、层状、碎裂和散体结构的岩体表现出不同的工程行为特征; 岩体结构具有级序性,结构面从深大断裂到小节理,结构体从地块到岩块,不同级别的岩体具有不同的力学意义(谷德振, 1979)。
(2)对岩体工程地质科学问题本质的揭示。“岩体结构控制论”(孙广忠, 1988, 1993; 孙广忠等, 2016)揭示了岩体工程地质力学行为最本质的规律。岩体结构的控制作用主要表现在它对岩体工程性质、岩体变形破坏模式、岩体渗流特性、岩体工程问题边界条件,以及地质环境作用规律的控制。岩体结构控制通过结构力学效应来实现,主要包括不连续效应、弱面效应和爬坡角效应等结构面力学效应,以及各向异性效应、尺度效应等结构面组合的力学效应。
(3)对岩体工程地质科学问题视域的拓展。岩体工程地质力学强调岩体和工程结构的统一性,形成了用力学理论分析处理工程结构与地质体相互作用规律的工程-地质-力学基本思想。王思敬等(2004)提出人类工程活动与地质环境相互依存又相互作用的思想。孙广忠(1993)将与地质体相关的工程称为地质工程。为了保证工程效用和地质安全,人们既要充分发挥岩体自身的积极潜力,又要采取一定的工程措施以提升这种潜力。
按照现代工程地质动力学观点,岩体工程地质力学的基本内涵可以表述为:岩体及其特性是地球动力学作用结果的“动力成因观”、岩体工程行为是人类活动与地质环境相互作用响应的“动力作用观”,以及工程地质防灾途径是调节工程与地质环境相互作用的“过程调节观”(伍法权, 2011)。
1.2 岩体工程地质力学的历史贡献
岩体工程地质力学不仅对于中国工程地质学科理论发展是一个里程碑,在指导我国大规模岩体工程实践、技术规范体系建设、专业教育与人才培养中也做出了不朽的历史贡献,体现出它巨大的核心价值。
1.2.1 支撑我国重大岩体工程建设
作为岩体工程地质力学的早期实践,谷德振先生曾参与和指导治淮工程、长江大桥、南水北调、三峡工程、成昆(湘渝、湘黔)铁路、金川矿山及各类国防地下工程等一万多项,并曾获“南京长江大桥新技术”、“葛洲坝二、三江及其水电机组”、“成昆铁路建设”等3项国家自然科学奖特等奖。
毋庸讳言,迄今为止的国家大型基础设施建设工程,包括大型水利水电工程、铁路公路交通工程、大型矿山工程、各类深部工程和国防工程,以及山区城镇建设等,一半以上是岩体工程。这些工程建设的论证、勘察、设计、施工中,无一不渗透着岩体工程地质力学思想的指导。
1.2.2 引领我国技术规范体系建设
建国70多年来,我国已经逐步形成和完善了自己的技术标准体系。据统计,目前已有与工程勘察、试验测试、设计、施工相关的国家标准118部,行业和地方标准448部(化建新等, 2018),且有一大批团体标准正在陆续撰写和发布实施。这些技术标准中,与岩体相关的部分大多承袭了岩体工程地质力学和结构控制论的基本思想,当然也融合了国外的一些先进经验。几十年来岩体工程行业的规范化行为,已经使岩体工程地质力学的思想成为人们的科学技术常识和专业分析判断的依据。
1.2.3 指引和支撑专业教育与人才培养
专业教育与人才培养是科学技术传承与发展的基本途径。据大学生必备网统计,我国设立地质工程、岩土工程类专业的高等院校有154所。这些高校的地质工程和岩土工程类教材中,有关岩体特性和力学行为的表述多数融入了岩体工程地质力学的思想,也有部分承袭了苏联“成因演化论”体系。
据住房和城乡建设部《2018年全国工程勘察设计统计公报》(中华人民共和国住房和城乡建设部, 2019),全国工程勘察设计行业从业人员447.3万人,其中专业技术人员188.2万人。这是一支我国自己培养起来的中坚力量,其中多数承接了岩体工程地质力学思想的熏陶和相关技术规范的训练。近年来一批杰出人才逐步走上了工程地质国际舞台的中心。
2 岩体工程地质力学的传承与发展——统计岩体力学理论探索
2.1 统计岩体力学探索的背景与初心
以往我们更多在地表和浅地表带、常温带、常地应力区,以及地震安全岛区域从事人类工程活动,所接触的是常规地质环境。我们对于这类环境有了较多的认识和处理经验。但是近几十年来,随着人类大规模工程建设向深山、深地,以及未来向深海、深空的推进,工程建设逐渐遭遇到“极端地质环境”,例如高地应力、高(低)地温、高地震风险等恶劣地质环境条件,以及由此引起的岩爆、大变形、高温、冻融,以及动力变形破坏等,采用以往理论已经不能很好地解决工程地质问题。
这就为岩体工程地质学科提出了两方面要求,一是要丰富和提升岩体工程地质学科的基础理论,二是要发展岩体工程地质信息获取、工程灾害分析评价与控制技术。
统计岩体力学探索的初心就是,立足地质基础,建立工程与地质相互作用的岩体力学理论,以支撑岩体工程地质力学的基础研究,我们把它叫做理论岩体力学; 同时发展支撑工程应用的便捷技术体系,我们把它叫做工程师岩体力学。30年来,统计岩体力学探索正是基于这样的初心走过来的。
近年来,统计岩体力学的思想方法和理论系统已经逐渐得到业界的认可。继1993年《统计岩体力学原理》一书出版之后,论文“Principles of statistical mechanics of rock mass”被纳入RockMechanicsinChina文集参加1995年日本东京第8届国际岩石力学大会(Wu et al., 1995),并得到Hudson等的高度肯定。文稿“统计岩体力学基本理论”被载入《中国岩石力学与工程世纪成就》(王思敬, 2004)。作者也因为建立统计岩体力学理论体系获得2020年国际工程地质与环境协会学术终身成就奖,并被提名参与中国岩石力学与工程学会-JournalofRockMechanicsandGeotechnicalEngineering第一届钱七虎讲座(Wu et al., 2021)。以统计岩体力学为基础的《工程岩体参数计算与岩体质量分级技术规程》已由中国岩石力学与工程学会发布,中国标准出版社出版(伍法权等, 2021b)。
2.2 统计岩体力学的思想方法
概言之,统计岩体力学的基本思想方法借鉴了经典统计物理学的思想(王竹溪, 1956),即用分子运动论方法解剖微粒的力学行为,获得介质系统的宏观力学行为描述,这正符合岩体的基本特性。按照岩体结构和结构控制论的思想,岩体是由大量结构面及其切割成的结构体组成的系统,岩体的力学行为正是其中各结构面和岩块细观力学行为的宏观体现。
统计岩体力学的体系结构大致如图 1所示。
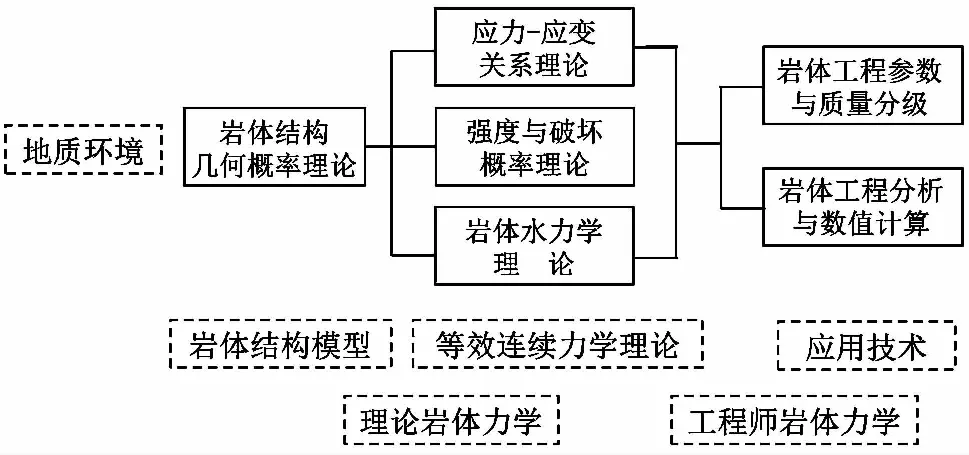
图 1 统计岩体力学的体系结构Fig. 1 The frame of the Statistical Mechanics of Rock Masses
岩体的地质环境,包括地应力、地下水等是统计岩体力学的基本背景,一切理论分析和技术工作都是在这个环境条件下展开的。采用岩体结构几何概率理论建立的岩体结构模型是后续力学理论据以建立的基础,这也正是岩体结构控制论基本思想的体现。以岩体结构模型为基础建立的岩体应力-应变关系理论、岩体强度与破坏概率理论以及岩体水力学理论构成统计岩体力学的基本理论框架,分别解决了岩体工程中变形、强度和渗流特性分析的3个基本问题。作为理论向工程应用的延伸,岩体工程参数和岩体质量分级、岩体工程问题分析和数值计算则是统计岩体力学基本的应用技术。
从总体上看,以岩体地质环境为背景,岩体结构模型和3个基本的等效连续力学理论构成了理论岩体力学部分(伍法权, 1993); 而基于岩体地质环境和理论模型的应用技术则构成了可操作性较强的工程师岩体力学部分。
2.3 统计岩体力学的基本原理
统计岩体力学的理论系统主要体现了如下基本原理:
2.3.1 岩体结构几何概率原理
岩体结构控制论的核心理念是:岩体结构是岩体一切力学行为的基础。以往岩体力学理论研究的根本困难就在于缺少恰当的岩体结构理论。Hudson等人探索建立了岩体结构几何概率分析与随机模拟技术(Husdon et al.,1983; Priest et al.,1983),引入尺度分析技术,使得岩体结构分析从早期的角度分析进入了全面的几何概率分析新阶段(潘别桐等, 1989); 也使得我们有可能从几何概率模型中提炼出岩体结构的参数模型。这就为统计岩体力学的建立奠定了岩体结构理论基础。
岩体结构几何概率理论具有如下功能特点: ①岩体结构各要素具有特定的概率分布,可以方便地获得其特征值,如优势倾向与倾角、平均间距、平均迹长、平均隙宽等; 而另一方面,这些特征值又与岩体结构形成的力学原因有深刻的联系,如不同的应力状态决定了各结构面组之间的产状组合关系; ②岩体结构各要素可以通过几何概率方法联系起来,从而建立起一些描述更复杂结构特性的参数,如在结构面形心服从均匀分布时,其体积密度与其法向密度、平均半径具有确定的几何概率关系; 由露头面上结构面平均迹长可以求得结构面平均半径,由各组面法向密度和法线与测线夹角可以求得测线RQD,等等。这些特点使得几何概率理论成为支撑岩体结构模型建立的强大工具。
岩体结构几何概率参数模型由一系列参数的分布和特征值,以及描述岩体结构整体特征的参数组成,包括结构面产状、迹长和半径、间距、隙宽的分布和特征值、面积和体积密度、RQD、最大半径和隙宽、连通率等特征参数。以这些参数为基础,引入恰当的力学或水力学理论,即可建立起岩体的各种力学模型。
2.3.2 断续介质连续等效的断裂力学能量原理
按照岩体工程地质力学的认知,岩体结构是由一系列岩石块体和结构面网络组成的。结构面的存在使得岩体成为断续介质,因此不能简单地按照连续介质进行力学分析。但是断裂力学为我们提供了从非连续介质到连续介质力学分析的桥梁。
按照弹性断裂力学理论(范天佑, 1978),在一定的外力作用下,岩体单元中任一埋藏型结构面都可能发生法向拉压和切向错动变形(图 2)。在准静态和忽略热耗散的情况下,外力引起结构面这些变形所做的功都会以弹性应变能存储在结构面周边的连续岩石中:
(1)
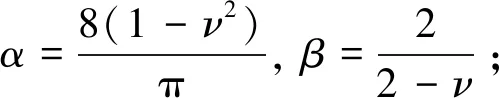
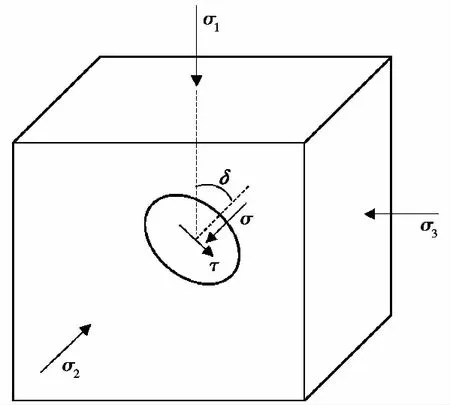
图 2 岩体单元和结构面受力图Fig. 2 Force diagram of an element and discontinuity
由于应变能是标量,因此可以直接进行加和运算。这就是应变能可加性原理。由此,单元中任一结构面的应变能都可以直接加入到周边连续岩块中。这就在力学上实现了由断续介质向连续介质的等效,为采用连续介质理论分析断续介质的力学行为奠定了基础。
经过一定的数学力学推演,我们可以得到裂隙岩体的等效连续介质应力-应变关系(伍法权, 1993):
eij=Cijst·σst
(2)
式中:σ、e为作用于岩体单元的应力张量和由此产生的应变张量, 下标指示方向性;Cijst为反映岩体多种地质因素作用规律的四阶弹性柔度张量。
2.3.3 岩体结构-应力协同控制原理
岩体结构控制论是岩体工程地质力学的核心思想,它指出了决定岩体工程行为的本质原因。
近几十年来,岩体工程向深山、深地迅速拓展,大量遇到高地应力环境。岩体在深部等高地应力条件下,结构面往往会发生“应力锁固”; 即使在岩体开挖时,某些部位特定方向的应力集中也会导致结构面的应力锁固。在这些情况下,岩体结构控制可能失效,转而主要受应力控制。另一方面,岩体开挖引起差应力增大,也可能诱发部分锁固结构面的“应力解锁”,导致结构控制激活。由此可见,存在岩体的“结构-应力协同控制”机制。
岩体结构-应力控制及其转换由结构面上的剪切变形驱动力决定。结构面剩余剪应力,即该面上剪应力与抗剪强度之差(而不是剪应力的全部),是结构面发生剪切变形的真正驱动力。我们定义比值系数h为剩余剪应力与剪应力t之比:
(3)
式中:c、φ为结构面的黏聚力和摩擦角。
在受压条件下,结构面抗剪强度s=c+σtanφ是一个由法向应力σ决定的潜在极限值, 在实际过程中是由剪应力t诱发而产生的被动反作用力,与t相等,符合牛顿第三定律,此时有h=0,指示结构面被应力锁固,而岩体处于应力控制状态; 仅在剪应力t>c+σtanφ时,才会出现剩余剪应力h>0,此时结构面被应力解锁而处于结构控制状态。而在结构面受拉应力作用张开时,显然有s=0,h=1。
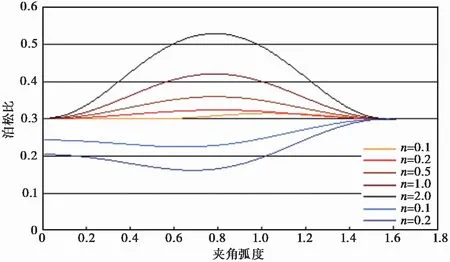
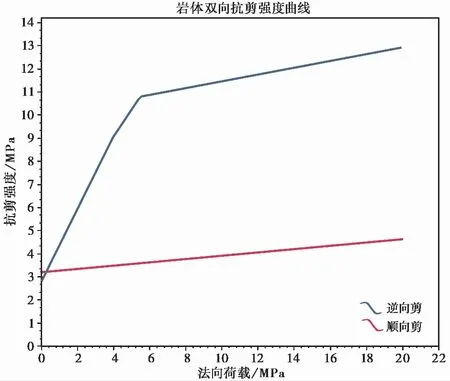
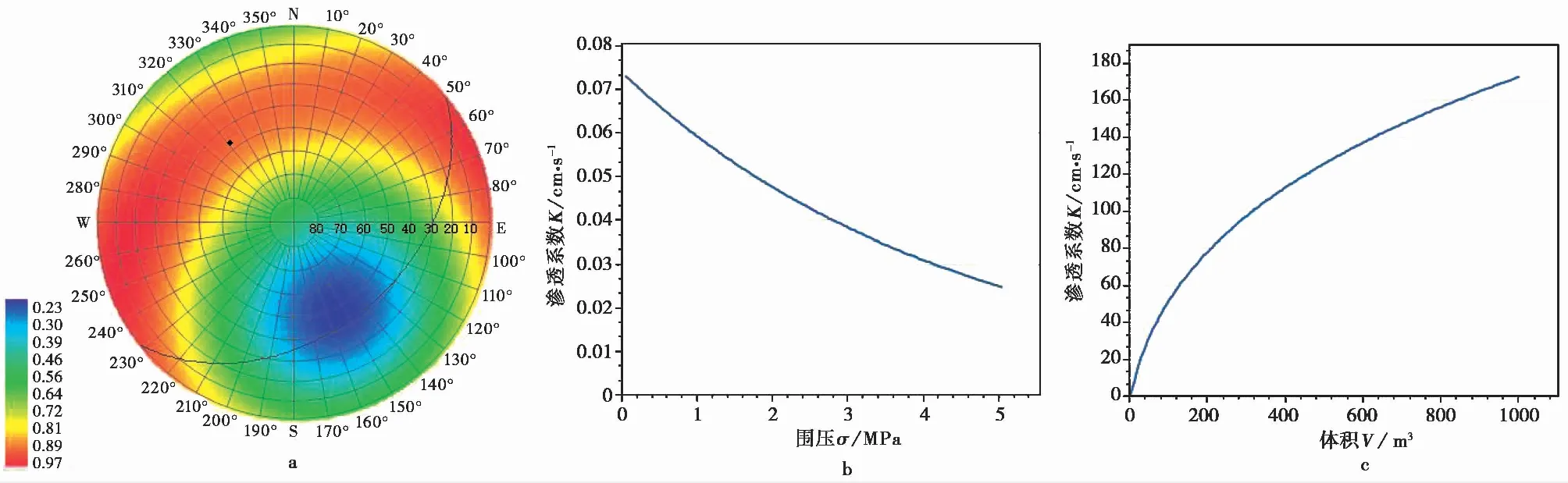
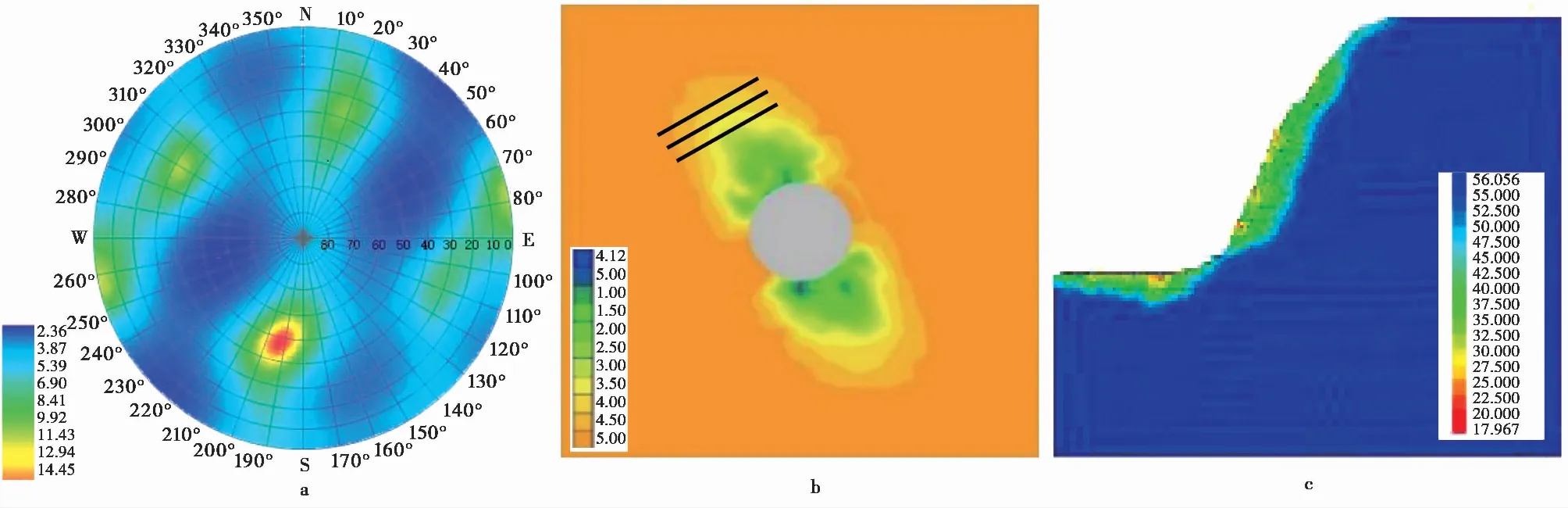
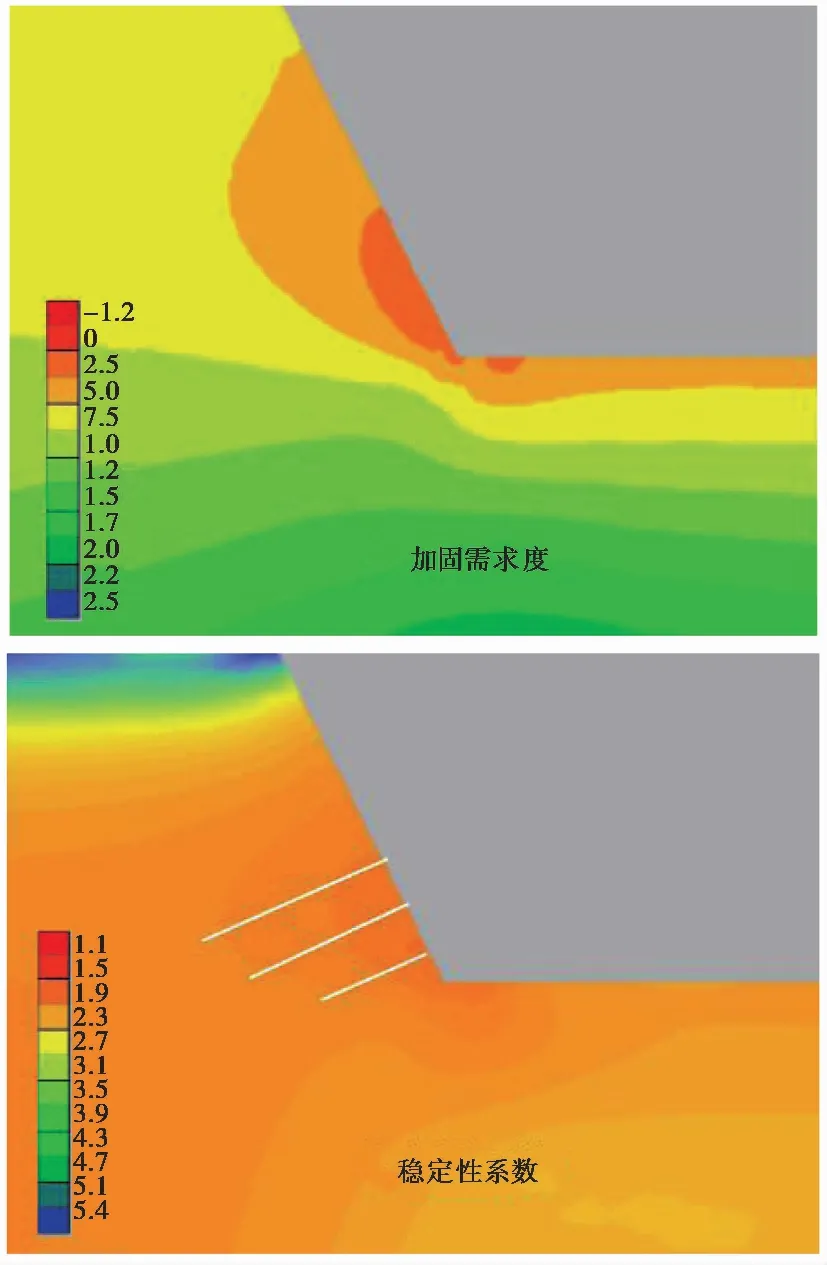
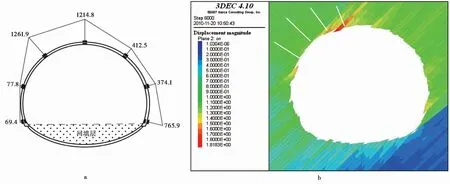
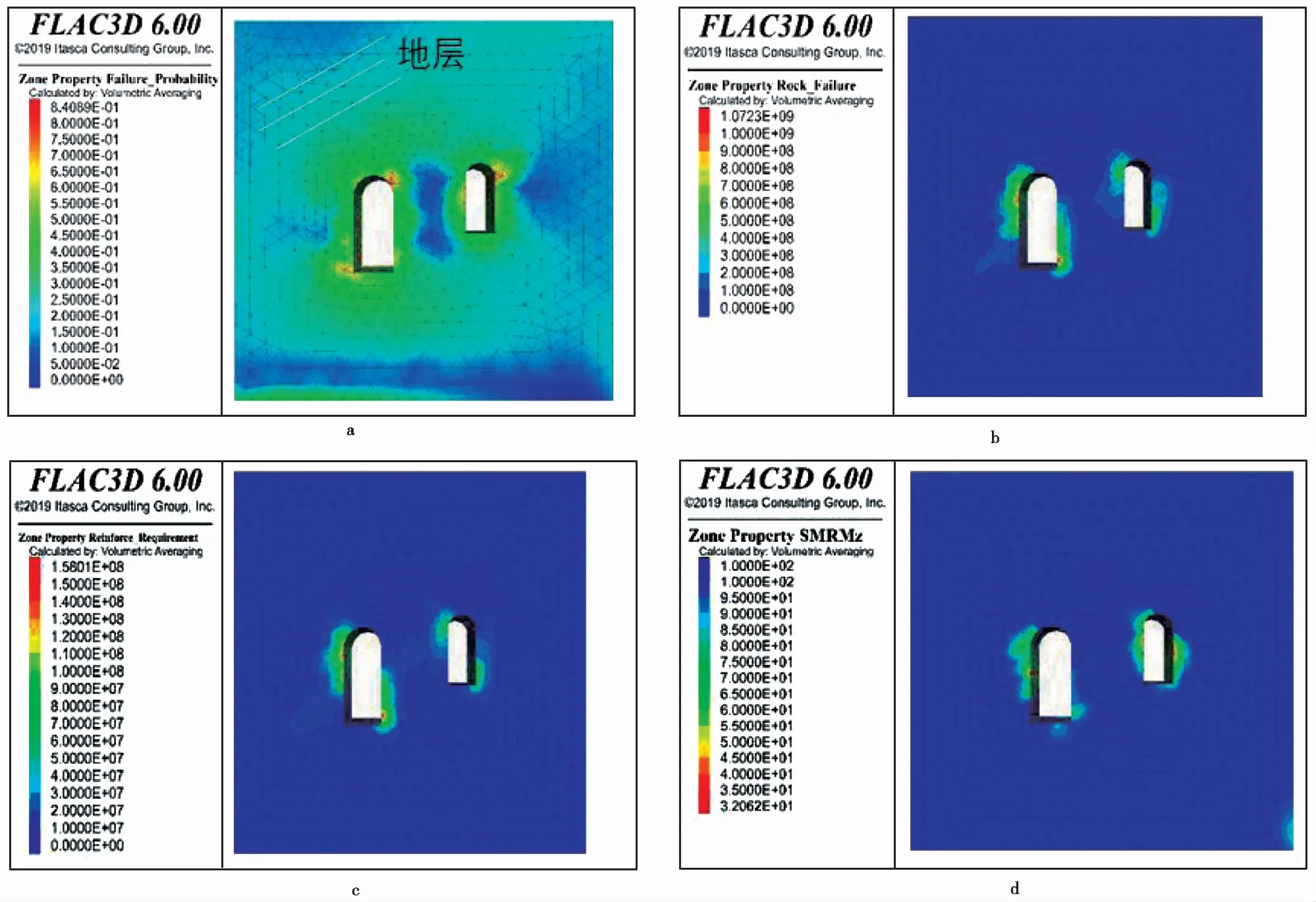
因此,h的数值指示了结构面发生剪切变形的可能性大小,也是岩体结构-应力控制的转换开关,即h=0和0 2.3.4 岩体强度的弱环控制原理 一个岩体单元包含了众多的结构面和岩石块体元素,该单元体的强度将受其中强度最低的元素,特别是结构面强度的控制。这就是岩体强度的弱环控制原理。岩体强度弱环控制原理是统计岩体力学中岩体强度理论建立的思想基础,也是岩体结构控制论的具体体现。 大量试验研究表明,岩石块体的强度具有显著的随机特性,通常遵从受弱环控制的Weibull分布(Weibull, 1939; 山口梅太郎等, 1982),而Weibull分布正是可靠性理论的基础(曹晋华等, 1986)。由岩块的强度分布可得到其最可能的单轴抗压强度值σc和方差S2分别为: (4) 式中:σ0为岩石单轴抗压强度的基本值;m为强度的分散性系数, 其值越大,分散性越强,m一般取值1~3。 另一方面,由于岩体中结构面的几何要素,无论是产状、尺度、密度都具有随机性,因此结构面的强度也具有显著的随机性。我们知道,在相同应力状态下,一组结构面的强度由其中最大尺寸结构面决定,它同样符合Weibull分布规律。由此可见,岩体的强度问题是一个受弱环控制的可靠性问题,岩体的强度判断应该由力学判据和破坏概率联合判断。 按照弱环控制思想,统计岩体力学将等围压下岩体抗压强度用统一的库仑强度方程和破坏概率P表述: (5) 式中:σ1为岩体的抗压强度,σ3为围压;Ti、Ri为反映岩石和结构面力学效应的参数;i为下标,i=0代表岩石,i=1, 2…N代表结构面组号,下标c指示临界值;λv、V为结构面体积密度与岩体单元的体积;k、m为Weibull函数的拟合参数。 从式(5)第2式还可以看出,岩体的破坏概率具有显著的体积效应,这也是弱环强度系统的共同特征。 2.3.5 断续裂隙网络渗流力学原理 水力渗透特性是岩体重要的工程性质。早期的岩体渗流力学模型是以贯穿型裂隙网络为基础提出的(Louis, 1974),此后也有不少表述裂隙网络连通率的经验形式。20世纪80年代有了岩体结构面网络随机模拟技术后,通过计算机可以搜索结构面连通网络,并以此为基础开展岩体渗流的数值模拟。 统计岩体力学认为,岩体的渗流实际上是沿结构面网络中连通部分的渗流,并以结构面几何概率分析为基础,提出了结构面组间连通率η的计算模型(伍法权, 1993)(图 3): (6) 图 3 节理连通性示意图Fig. 3 Schematic diagram of the connectivity of joints 由此,岩体单元的渗透张量可以写成: (7) 以上述原理为基础,统计岩体力学对几个重要的问题进行了拓展。 2.4.1 裂隙岩体的本构模型 建立岩体的本构模型是岩石力学界几十年来的热门而困难的课题。早期人们尝试了各种穿透性结构面切割的块体叠加模型。20世纪80年代日本学者Oda提出了岩体的结构张量,发展了基于结构张量的岩体本构模型(Oda, 1983, 1986),但至今尚未被岩石力学领域广泛接受。学者们引入损伤力学思想,探索建立岩体的损伤力学模型(Kawamoto et al.,1988; 周维垣, 1990),掀起了岩石力学界持续几十年的损伤力学热,但由于损伤力学源自一维金属杆件拉伸损伤研究,使其在三维受压的岩体研究受到诸多限制。 按照连续介质力学的模式,将岩体的SMRM弹性应力-应变关系模型式(2)和强度模型式(5)第1式(即屈服准则)组合,形成了统计岩体力学的岩体本构模型(Wu et al., 2021): 式中:e0ij为岩体单元中岩石的应变; 其他符号意义同前。 本构模型(8)为任意边界条件下工程岩体变形和破坏的统计岩体力学理论分析和数值计算提供了理论基础和可能性。 2.4.2 岩体的全过程变形解析 我们知道,岩石的全过程变形曲线是在刚性伺服机出现后通过试验获得的,而岩体则暂未获得全过程变形曲线。 但是,以岩体本构模型式(8)为基础解析岩体的变形与破坏过程,可以建立岩体的全过程变形曲线。岩体变形与破坏过程解析的基本思想是,对于每个应变步,在荷载方向上始终取岩体的变形应力和强度应力的小值; 当强度应力达到岩石的强度时,岩石破坏,扣除其单轴抗压强度。 图 4 岩体全过程变形曲线Fig. 4 The complete deformation curves of rock mass 岩体的变形与破坏过程可由式(9)描述: (9) 由上式作出的全过程变形曲线如图 4。 2.4.3 高储能岩体特性与岩爆机理模型 岩体在特定的应力环境中会产生变形,并储存一定的应变能。按照弹性理论,岩体储存的应变能与应力和应变的乘积成正比。一般来说,越坚硬的岩体越容易在高应力下储存较高的应变能。高储能岩体就是指这类储存较高应变能的岩体。 高储能岩体一般具有如下特性:(1)岩体结构压密,包括岩块的压密、岩块中微裂隙和宏观结构面的闭合和压密。(2)岩体结构控制失效。当应力较高时,岩体中部分或全部结构面可能发生“应力锁固”,岩体的力学行为将转而受应力控制。(3)岩体波速异常。按照岩体结构控制论的思想,由于结构面的力学效应,岩体的声波纵波速度一般小于岩块,但对于高储能岩体,岩体的波速可以高于取芯岩块达40%,这就是所谓的“波速异常”。当然,如果能同时测得岩体和原位岩块的波速,其比值可能仍然会小于1.0。 高储能岩体的波速异常也为我们预示了一条研究岩体受力状态的可能途径:测得取芯岩样的纵波速值,再对同样的岩石施加不同围压测量波速值,可研究波速随围压的变化关系。由此可以通过测量岩块原位波速反推岩体地应力。 上述各种现象提示我们,应力在一定的范围内的增高可能改善岩体的工程性质,因此也会提升岩体的质量,而不应当简单地进行岩体质量的应力折减。 岩爆是近几十年来岩体工程中的一个国际难题(张镜鉴等, 2008)。现有对岩爆机理的认识和岩爆判据多以库仑压剪破裂理论为基础。按照这一理论,岩爆的破裂角为库仑剪破裂角。但是大量岩爆现象表明,岩爆破裂角常可以小至3°~5°,甚至0°(即劈裂)。 而按照库伦剪破裂角,即45°-φ/2, 即使岩石内摩擦角达到60°,库仑剪破裂角仍然不小于15°。这表明采用库仑压剪破裂理论解释岩爆机理并建立岩爆判据是不符合客观情况的。 我们知道,库仑强度理论并不能很好地适用于围压为张应力,甚至是低围压的情形。而事实上大量岩爆正是发生在开挖岩体表面,其围压常常接近于0,甚至存在次生张应力,岩石的破裂很难由库仑强度理论描述。 基于岩体的本构模型(式(8)),我们提出了岩爆的控制方程: (10) 式中: 第1式为岩体沿最小主应力方向的应变e33,由岩块应变e033和结构面应变组成; 第2式为格里菲斯强度判据(Jaeger et al., 1979),σ11、σ33为最大和最小主应力,σc为岩块的单轴抗压强度。 我们知道,格里菲斯强度判据能够较好地反映张性条件下的岩石破裂过程,在低围压条件下也能很好地与库仑强度理论吻合。 根据格里菲斯理论,岩石的破裂角可由下式计算: (11) 随着围压σ3的减小, 破裂角将减小; 直至为0, 此时为沿张性围压力方向的拉张破坏。可见,格里菲斯理论可以完美地解释岩爆机理和破裂角变化。 另一方面,比较单轴压破坏和单轴拉伸破坏所消耗的能量发现: (12) 可知张性岩爆消耗的能量远小于压剪性岩爆,也可以证明张剪性岩爆则介于其间(Wu et al.,2010)。 张性岩爆的机理模型(式(10))和岩爆按应力状态排序的提出,是一次观念的改变,对于岩爆机理研究和工程控制具有重要的意义。 2.4.4 圆形硐室围岩弹性变形解析解 圆形硐室围岩变形的解析解来源于平面应变问题的弹性解,它的重要意义在于提出了不同应力边界条件下圆形硐室围岩应力和位移的理论分布,为各类不规则形态地下工程问题的围岩应力与变形分析,特别是应力集中特征分析提供了参照。 但是经典的圆形硐室解析解是以均匀、连续、各向同性弹性介质为前提导出的,并不适用于各向异性介质。例如层状介质隧硐围岩的变形就显著地受岩层产状的影响,即使在对称的应力边界条件下也表现出强烈的非对称变形,常导致对称设计的隧道支护系统失效。这是目前我国西部铁路、公路、引水隧洞工程中十分常见工程地质问题。 统计岩体力学以各向异性岩体的本构模型为基础,推导出圆形硐室围岩变形的解析形式,不仅合理反映了岩体结构对隧硐围岩变形和弹性围岩压力的控制作用,也为围岩有针对性的定向和主动加固提供了科学技术支撑。值得提及的是,迄今各向异性围岩的塑性半径和塑性围岩压力解仍未能提出。 由于岩体结构力学效应强烈控制着岩体变形和应力场的分布,以经典弹性介质圆形硐室围岩变形解析解揭示的许多规律,以及由此形成的思维定式将被打破。例如,在对称自重应力场作用下,倾斜地层圆形硐室的最大变形和最可能的压破坏区将不再是硐室水平半径的端点部位,而是岩层与硐壁切点部位。同时这些部位岩体的模量、强度、岩体质量级别都将显著降低,而破坏概率、岩爆发生的可能性,以及加固的需求度都将显著提升。 图 5显示了以60°倾角倾向右侧的单斜层状岩体中圆形硐室围岩径向位移和SMRM岩体质量级别(参见本文3.6.1节部分内容)分布图。 统计岩体力学通过一系列应用技术的延伸,达到服务工程实践的目的,也由此将理论岩体力学变为工程师岩体力学。统计岩体力学从岩体数据的现场采集技术、岩体工程参数计算、岩体工程问题的数值分析角度发展了系统的应用技术,基本满足岩体工程实践的需求。 图 5 单斜层状岩体圆形硐室围岩解析解Fig. 5 The analytical solution of a circular tunnel in inclined layersa. 围岩单元体受力; b. 围岩位移; c. 围岩SMRM质量分布 我们知道,工程岩体不在实验室,而可能在高山峡谷,或者地下深部。岩体的数据需要现场采集,通过工程地质调查和勘察获取,多数需要爬山涉水现场测量,或者通过钻探采样、运输、制样、试验等繁复复杂的工作流程,既耗时、耗力、耗资,也难以保证数据的可靠性。另一方面,按照岩体结构控制论的思想,岩体的性质也不能用实验室岩石力学试验数据代替或者简单推断。因此,岩体数据的现场采集技术成为岩体工程的基础环节。 近年来,我们依托浙江岩创科技有限公司与绍兴文理学院的联合实验室,探索发展了岩体数字化技术系统,包括SMRM岩石力学背包实验室、岩体结构的采样窗和非接触测量与智能解译技术,为系统完成岩体结构与岩石力学现场测试提供了技术手段。 SMRM岩石力学背包实验室将电伺服岩石点荷载仪、岩石单轴和三轴仪,岩石直剪仪、结构面摩擦仪,以及取样钻机、切磨样机集成组合于一体,并采用电池供电,实现了无人、无电环境的现场岩石与结构面力学测试(图 6)。背包实验室通过无线数据采集和传输,采用手机电子野簿记录和连接SMRM云计算平台,实现了岩体设计参数计算和工程问题分析的一站式工作模式。 图 6 SMRM岩石力学背包实验室组件Fig. 6 Parts of the portable SMRM rock mechanical laboratorya. 点荷载仪; b. 直剪仪; c. 三轴仪; d. 结构面摩擦仪;e. 取芯钻机; f. 试件切磨机 为了控制现场岩石力学试验样本数量,SMRM云平台设计了试验样本数统计与跟踪函数拟合功能,可以即时计算各次试验对数据拟合优度的贡献,并适时反馈指导现场测试样本量控制。 值得一提的是,近年来绍兴文理学院的师生们(林军等, 2018; 沙鹏等, 2020a; 伍法权等, 2021a; 王兆远等, 2022)利用自制的背包实验室仪器与MTS试验系统比较研究,对岩石点荷载强度和抗压强度的尺寸效应进行了有意义的研究,发现了不同于Weibull强度尺寸效应衰减的规律,即在小于5~6cm尺度范围内岩石强度随尺度增大而增大; 只有当试件尺寸大于这个数值时符合Weibull强度衰减规律。这一发现可能导致对ISRM关于岩石力学测试试件标准尺寸建议的质疑(图 7)。 图 7 小尺寸岩石强度的尺寸效应Fig. 7 The size effect of strength of small rock samplesa. 粉砂岩; b. 花岗岩(De为试件等效直径,Is(50)为标准尺寸点荷载强度) 对于岩体结构数据采集,以往多采用平硐编录方法,沿硐测量和绘制展示图,一般记录>50cm结构面。这类编录只是获取了对岩体稳定具有控制意义的结构面数据。20世纪80年代,Hudson等人(Hudson et al.,1983; Priest et al.,1983)发展了岩体结构精测线测量与数据的几何概率分析方法,但这种方法对数据测量要求较高,数据的几何概率处理流程也较为繁琐。而与精测线法几乎同时代,Kulatilake et al. (1984)提出了岩体结构采样窗测量方法,则体现出相对的便捷性。近年来,统计岩体力学以采样窗法为基础,发展了岩体结构各类参数的提取方法(伍法权等, 2021b)。张恺等(2019)、张文等(2020)、张杨等(2020)、王明等(2019)、李丽慧等(2019)分别采用无人机倾斜摄影等非接触测量方法对岩体结构数据采集技术、三维裂隙网络模拟及计算方法进行了研究。 岩体结构智能解译技术则是近年来广受关注的热点技术。该项技术运用无人机倾斜摄影、三维激光扫描和近景数字摄影等非接触测量技术,获取露头面3D点云数据,并开发了基于点云数据的岩体结构解译技术。近几年来我们自主研发了岩体结构智能解译软件(Kong et al.,2020),基本解决了即时便捷获取岩体结构各类参数,建立岩体结构几何概率模型,乃至进行岩体中的块体识别和块体稳定性评价等技术问题(图 8)。 岩体结构参数是工程中评价岩体完整性的重要内容,常被用于岩体质量分级的基本指标。常用的岩体结构参数包括:结构面的体积密度λv、任意方向上的RQD值、任一组结构面的最大半径am或最大隙宽tm,以及结构面组的连通率η等。 3.2.1 结构面体积密度λv λv(或体积节理数Jv)是岩体质量分级的基本指标,许多技术规范中采用体积节理数Jv换算岩体的完整性指标Kv。统计岩体力学定义结构面体积密度λv为单位体积内结构面形心点数,单位为条/m3。 大量实测数据表明,一组结构面的尺度和密度服从负指数分布。按照岩体结构的几何概率理论,一组结构面的体积密度可按下式计算: (13) 3.2.2 任意方向RQD RQD是刻画岩体结构完整性的常用指标,也是岩体质量分级的基本指标。空间任意测线L方向的RQD值可由下式计算: (14a) 式中:λs为测线上结构面交点的密度。当测线无限长时有: RQD=e-λst×100% (14b) 由于RQD值随空间方向变化,将其值作出赤平投影图,可以分析岩体结构的空间各向异性。实际工程中可以计算全空间方向的平均RQD和最小RQD来评价岩体的结构性质,并可以定义岩体结构各向异性指数来描述岩体结构的各向异性特征: (15) 式中:RQDmin、RQDmax为全空间方向中RQD的最小值和最大值。 3.2.3 一组结构面最大半径am和最大隙宽tm 该两项指标分别对于岩体的强度和渗透性能具有重要的控制作用。一组结构面尺度最可能出现的最大半径和最大隙宽分别为: (16) 图 8 基于3D点云的岩体结构智能解译技术Fig. 8 The 3D point cloud based interpreting techniques for rock mass structurea. 岩体结构解译软件界面; b. 岩体结构实景; c. 岩体结构与解译块体 对于裂隙岩体,由于岩体结构力学效应,其变形特性已经不能简单采用弹性模量和泊松比两个常数来刻画。但按照工程习惯,我们仍然沿用弹性模量(或变形模量)和泊松比作为岩体变形性能指标。在统计岩体力学中,尽管沿用了弹性力学(王龙甫, 1979)的原始定义方式,但岩体的弹性模量和泊松比却反映了各类地质因素的影响,成为这些因素的函数。 3.3.1 弹性模量 按照弹性力学的定义,岩体弹性模量Em可直接从式(2)岩体的应力-应变关系模型求取,即在荷载σ11方向上应力与应变的比值: (17) 式中:E为岩石的弹性模量;n1=cosδ,δ为结构面法线与荷载方向夹角;k为结构面法向应力状态系数,当结构面受压闭合时k=0,而受拉张开时k=1;h由式(3)求取,其他符号意义同前。 显然,式(17)右端分母中的求和部分反映了各组结构面力学效应,且均为正值,这表明结构面作用的存在导致了岩体弹性模量的弱化。 图 9 岩体的弹性模量Fig. 9 Elastic modulus of rock massa. 弹性模量赤平投影图; b. 弹性模量-围压曲线 由于弹性模量的弱化,因此可以基于岩体与岩石弹性模量的关系定义岩体变形性质的弱化系数ζE。而由于各向异性,弹性模量计算值可以用赤平投影图表示(图 9a),并做出任意方向截面的方位分布玫瑰图。由此也可以定义岩体变形性质的各向异性指数ξE。上述两个指标定义如下: (18) 也可以做出不同荷载下岩体弹性模量随围压的变化曲线(图 9b)。 3.3.2 泊松比 以往工程应用中常按岩石参数取岩体泊松比数值,一般为0.2~0.4,并认为其取值变化范围较小,对岩体力学行为影响不大。但统计岩体力学已经证明,受压状态下的岩体泊松比常常远大于岩石的泊松比。这已经成为一个不可忽视的客观现象。 同样,按照弹性力学的方式,我们定义岩体在x1方向荷载作用下沿任意x2方向的泊松比如下: (19) 式中:e11、e21为岩体在荷载σ11方向的应变和垂直于荷载的任意x2方向的应变,其他符号意义同前。 比较式(17)可见,不仅岩石块体的泊松比ν,其他影响弹性模量的岩体结构和环境应力因素都影响着岩体的泊松比。图 10为含1组结构面的岩体泊松比随结构面法线与荷载取不同夹角(按弧度计)时的曲线。图例中n=λ为结构面的法向密度。 图 10 不同轴压下的岩体泊松比玫瑰曲线Fig. 10 Rose diagram of Poisson’s ratio of rock mass under different axial loads 图10中显示,受压条件下不同结构面密度的岩体泊松比一般大于岩石泊松比ν=0.3; 受拉条件下不同结构面密度的岩体泊松比一般小于岩石泊松比0.3。这就是岩体存在的“大泊松比效应”与“小泊松比效应”。 事实上,考察式(19),当岩体受等围压作用时,k=0,于是有 同时,当岩体受各向相等张应力作用时,结构面张开,k=1,h=1,将有vm21 3.3.3 系数h对岩体变形性质的控制 根据上述讨论,我们还可以考察受压的应力状态下结构面剩余剪应力比值系数h对岩体弹性模量Em和泊松比νm21的影响。由式(17)和式(19),当h>0时,结构面的力学效应存在,Em (20) 这就是前面提及过的结构面剩余剪应力比值系数h对岩体变形的影响,以及对岩体变形的结构控制和应力控制的转换开关作用。 岩体强度参数是岩体工程性质评价的基本指标。由于荷载施加能力的限制,目前直接测得的岩体抗压强度数据尚少。而岩体的抗剪强度通常采用现场大型剪切试验获取,但因目前考虑剪切方向与岩体结构面产状关系不足,数据分散性较大,可靠性不足。 3.4.1 岩体的抗压强度 统计岩体力学给出了岩体抗压强度的理论计算模型。在等围压条件下,岩体抗压强度可以采用式(6)计算。对于各向不等围压作用下岩体抗压强度,则应采用下式计算: (21) 式中: 第1式为岩石的库仑抗压强度; 第2式由结构面强度判据(式(22))(伍法权, 1993)导出: (22) 由于式(21)第2式左端ti含有轴向荷载σ11,而右端hi中也含有σ11项,两者构成了σ11较为复杂的隐函数,因此第2式中的强度值σ11只能通过一元二次方程求解。 对于等围压的相对简单情形,式(21)可以统一地表述为: σ1i=min(Tiσ3+Ri)i=0, 1, 2,…m (23a) 式中: (23b) 式中:i为下标,i=0为岩块,采用式(21)第1式计算,i=1, 2, 3,…m为结构面组号;δi为第i组结构面法线与σ1的夹角;ami为该组结构面的最大半径;φj、cj为结构面摩擦角和黏聚力; 其他符号意义同前。 岩体的全空间方向抗压强度可作出赤平投影图如图 11a,并可分别定义强度的弱化系数ζσm和各向异性指数ξσm如式(24)。也可以作出等围压条件下岩体的抗压强度曲线如图 11b。 (24) 3.4.2 岩体的抗剪强度 岩体的抗剪强度,以水平面为剪切面,铅直法向荷载为σ33,剪应力为σ31,结构面的抗剪强度可由判据式(22)取k=0导出。计算公式一般可以写为: (25) 从式(25)中解出σ31,即可做出σ31~σ33曲线。在水平面内任意转动剪切方位,获得该方位的岩体抗剪强度,由此可以做出抗剪强度的玫瑰图。 图 11 岩体的抗压强度Fig. 11 Compressive strength of rock massa. 岩体抗压强度赤平投影图; b. 抗压强度-围压曲线 图 12 岩体的抗剪强度-围压曲线Fig. 12 Curves of shear strength of rock mass vs confining pressure 作为特例,含一组结构面的岩体逆结构面倾向与顺向剪切强度可由下式计算: σ31=tan(φj±δ)σ33+ (26) 式中:δ为结构面倾角,在±号中逆向取第一运算符,顺向取第二运算符。 由式(26)可见,第1部分中法向应力σ33的系数即为库仑抗剪强度的摩擦系数, 显然逆向剪切(运算符取+号)时,摩擦系数tan(φj+δ)>tanφj,而顺向剪切的摩擦系数tan (φj-δ) 3.4.3 系数h对岩体强度性质的控制 考察式(21)和式(25)的第2式可以发现,无论是岩体的抗压强度还是抗剪强度,当任一组结构面上的剩余剪应力比值系数满足0 岩体的渗透性能、渗透系数的方向性、水岩耦合规律,以及渗透性能的体积效应是十分受关注的工程性质。 以岩体的渗透张量式(7)为基础,可以写出水力梯度mj方向上的渗透系数K,即: K=Kijmimj (27) 变换水力梯度方向mj,可以做出三维空间的渗透椭球和渗透系数赤平投影图(图 13a),并求出3个主渗透系数及其方向。 在考虑埋深和围压条件下,由于结构面隙宽t受其法向应力σ影响,t=t0e-ασ,因此可以作出水岩耦合曲线K-σ(图13b)。 图 13 岩体的渗透系数Fig. 13 Permeability of rock massa. 岩体渗透系数赤平投影图; b. 渗透系数-围压曲线; c. 渗透系数体积效应 近几十年来,岩体质量分级已经成为直接支撑岩体工程设计的基本参数。但是,现有的岩体质量分级系统大多建立在强度分级理念基础上,而对于软弱岩体的变形性质关注不够; 另一方面,工程岩体多数是沉积岩、副变质岩,具有层、片状结构,力学性质具有显著的各向异性特征,是现有的各向同性岩体质量分级所不能反映的,因此引发了诸多的各向异性修正的探索。 图 14 SMRM岩体质量分值分布Fig. 14 Distribution of the SMRM quality score of rock massa. 全空间方向赤平投影分布; b. 硐室围岩中的分布; c. 边坡中的分布 3.6.1 岩体质量的SMRM分级方法 由式(17)可见,岩体的弹性模量比较客观反映了各种地质因素对岩体变形行为的影响,也突出体现了岩体变形性质的各向异性。另一方面,已经有将岩体弹性模量与岩体质量分级相关联的研究成果,由此我们可以方便地基于岩体弹性模量建立岩体质量分级方法。采用RMR岩体质量分级的思路,可以建立SMRM岩体质量分级方法,其质量分值可由下列Serafim-Pereira经验公式计算: (28) 由于岩体弹性模量Em受岩体结构的影响具有方向变化性,因此SMRM岩体质量也自然反映岩体变形性质的各向异性,并可以通过赤平投影图表现这种方向变化性(图 14a); 另一方面,由于Em受应力状态的影响,工程岩体中的SMRM岩体质量也将随应力状态的变化而表现出空间变化性,由此可以借助于数值计算作出SMRM质量的空间变化云图。图 14b显示了单斜岩层(由图中的3条倾斜黑线示意)圆形硐室围岩SMRM岩体质量分布; 图 14c则为水平岩层边坡中的SMRM岩体质量分布。 3.6.2 现有岩体质量分级方法的各向异性改造途径 我们知道,现有国际普遍采用的岩体质量分级多为各向同性的强度分级,为了让这些分级方法适用于各向异性岩体,学者们尝试进行了各种修正(Zheng et al.,2018; Guo et al.,2020; Maazallahi et al.,2021),沙鹏等(2020b)对隧道层状岩体质量评价的BQ分级进行了改进探索。 另一方面我们注意到,常用的RMR和Q分级系统都将RQD作为基本指标,广受关注的GSI分级也是以RMR分级为基础发展起来的。业已证明,RQD指标是具有各向异性岩体结构指标,且已有成熟的计算方法。因此,将各向异性的RQD指标带入上述各种分级方法,这些方法将自然具有各向异性分级的功能。这就是我们所说的现有岩体质量分级方法的各向异性改造途径。 岩体加固是岩体工程的基本问题,也是一切岩体力学研究服务实际工程的落脚点之一。岩体加固以控制岩体变形、保障岩体稳定性为目标,通常依据变形和失稳控制所需的补强应力,并考虑安全余量进行设计。这类加固设计总体上体现了“被动加固”理念。 按照统计岩体力学的思想,岩体加固应该是采用有限的人工措施,激发和提升岩体的自稳潜力,达到有效控制岩体变形和稳定性的目的。我们将这一理念称为工程岩体的“主动加固”。 岩体的自稳潜力的核心是岩体自身的强度,可用库仑强度公式表述为: (29) 式中:φ为岩体的内摩擦角。 这就是说,岩体的内摩擦角φ、单轴抗压强度σc,以及侧向应力σ3的增加会对边坡在该点的强度,即自稳潜力σ1做出贡献。 考察式(29)可知,岩体的三轴强度σ1将以 tan2θ·σ3增加。例如当取θ=30°,60°时,岩体强度将分别按3σ3和14σ3比例增加。可见,我们可以提供锚索等方式适当提供σ3,以达到“四两拨千斤”的加固效果。 根据上述原理,我们提出了加固需求度(Δσ3)、加固前后的稳定性系数(K)、 锚固力等的设计计算方法。加固需求度是指保证岩体中一点达到极限稳定性所需的最小主应力与实际主应力之差,即: Δσ3=σ3c-σ3 (30) 它决定了需要外部提供的加固力和设计方法。图 15a给出了典型边坡加固需求度分布云图,图中取了Δσ3的负值为加固需求度。由图可见,均质岩土体边坡加固需求度最大的部位在: ①边坡面; ②边坡面下部1/3~1/2处。这就指明,坡面锚固是最优的加固方法,其次是抗滑支挡工程。 图 15 边坡主动加固计算图示Fig. 15 Sketch diagrams for active reinforcement of slopea 边坡加固需求度(图中取负值)分布; b 稳定性系数分布与锚固深度(图 15b中的白色直线) 统计岩体力学还提供了计算岩体中一点处稳定性系数的方法: (31) 据此可以做出岩体稳定性系数的点云图如图 15b。 按照式(30)和指定的安全系数,可以计算每束锚索的锚固力: (32) 式中:A为每束锚索覆盖面积;Ks为设计安全系数。 锚固方向可垂直于或小于坡面倾角,锚索长度达到与安全系数相等的稳定性系数等值线(图 15b)。 岩体主动加固方法已经在云南蜡寨水电站、刚果(金)宗果Ⅱ水电站(Wu et al.,2021)等工程成功应用,并获得良好的安全和经济效益。刘彤(2009)在中国科学院地质与地球物理研究所博士论文《小湾电站坝基开挖岩体卸荷特性及工程对策研究》中,在对小湾电站高地应力坝基开挖的岩体破裂控制技术进行了研究,依据岩体主动加固原理尝试了“预锚”和“速锚”的技术分析,即优先锚固再开挖和开挖后迅速锚固,都起到了通过保持原岩围压达到维持岩体强度的良好效果。 显然,由于力学原理的通用性,岩体主动加固方法也可以用于隧道与地下空间围岩的加固计算。按照前面介绍方法,通过计算找出围岩加固需求度较高、或岩体质量降低显著、或发生岩爆可能性较大、或围岩压力较高(图 16a)、或变形较大(图 16b)的部位,实施重点的预应力锚杆(索)加固补强(图 16b中的白色直线),这将是对现有设计方法,特别是对称设计方法的有效补充。 图 16 隧道围岩主动加固图示Fig. 16 Sketch diagrams for active reinforcement of tunnela. 隧道围岩压力实测分布(kPa); b. 隧道围岩变形较大部位锚固(图中的白色直线) 表 2 SMRM岩体参数计算系统计算参数表Table 2 Table of parameters can be calculated by SMRM calculation system 岩体工程参数是岩体工程设计的基础。岩体工程参数通常包括岩体的结构参数、变形参数、强度参数、渗透性参数,以及岩体动力学参数等。 近10年来,根据统计岩体力学原理,研发了SMRM岩体参数计算系统,并接入云平台。目前SMRM岩体参数计算系统实现了如表 2所示的各类参数计算,对于各向异性参数还可以计算弱化系数和各向异性系数。上述参数基本满足了现行岩体工程设计的参数要求。 SMRM岩体参数计算系统还基于FLAC3D数值计算平台,开发了本构模块JointModel,实现了统计岩体力学数值计算。JointModel以岩体结构几何概率参数模型为基础,引入SMRM本构关系(式(9)),计算功能包括:完全各向异性工程岩体的应力场、位移场,以及破坏概率、岩爆、岩体模量、强度、渗透系数、岩体加固需求度、稳定性系数等的云图。上述计算基本满足了岩体工程问题分析的要求。 图 17 锦屏一级水电站地下厂房围岩参数分布Fig. 17 Parameter distribution of the rock mass surrounding the underground powerhouse of Jinping Ⅰ hydropower stationa. 破坏概率; b. 岩爆; c. 加固需求度; d. 岩体质量等级 图 17以锦屏一级水电站地下厂房硐室群为例,采用FLAC3D-JointModel计算了硐室群围岩参数和岩体质量分布、潜在岩爆分布预测、加固需求度,以及稳定性系数分布。 毋庸置疑,岩体工程地质力学是中国工程地质学科发展的一座历史丰碑。40多年来,它不仅支撑了我国各类重大岩体工程建设,引领了我国相关工程技术规范体系的建设,也指引和支撑了我国岩体工程地质专业教育与几代人的人才培养。 统计岩体力学探索的初心是立足地质基础,建立工程与地质相互作用的岩体力学理论与便捷的应用技术体系,支撑岩体工程地质力学的理论研究和工程实践。 几十年来,我们初步建立起了统计岩体力学的理论体系,具象化和扩展了岩体工程地质力学的思想。借鉴经典统计物理学的思想方法,提出了岩体结构几何概率模型、断续介质连续等效的断裂力学能量原理、岩体结构-应力协同控制原理、岩体强度的弱环控制原理、断续裂隙网络渗流力学原理。以这些原理为指导,建立了裂隙岩体本构模型、岩体抗压强度和抗剪强度的库仑判据和破坏概率理论、岩体全过程变形分析方法、高储能岩体特性与岩爆机理模型、圆形硐室围岩弹性变形解析解。 以统计岩体力学的理论为基础,我们发展了岩体数据现场采集技术与装备、全空间方向岩体结构参数、变形参数、抗压强度与抗剪强度、渗透系数计算方法,以及各向异性岩体质量分级、工程岩体主动加固方法,开发了岩体工程参数计算系统和数值分析工具JointModel。这些技术为岩体工程师提供了丰富的应用工具。 统计岩体力学的建立对岩体工程地质力学理论与技术进步起到了重要的推进作用。我们将不断努力,促使统计岩体力学逐渐成熟,也使岩体工程地质力学的思想发扬光大! 致 谢本项目得到国家自然科学基金项目(90302011、41030749、41831290)、浙江省重点研发项目(2020C03092)的支持。 我们也希望借本讲座的机会,表达对岩体工程地质力学奠基人谷德振先生的深切缅怀!感谢为岩体工程地质力学发展做出贡献的前辈与同行们!感谢恩师王思敬先生、已故的恩师晏同珍先生,以及潘别桐、J.A.Hudson先生对统计岩体力学探索的指引!感谢祁生文、包含、伍劼、宋胜武、罗元华、单治钢、李星星、白忠喜、梁伟、乔磊、陈育民、戴振中等同事和朋友为统计岩体力学理论和技术发展给予的支持和帮助!感谢国家自然科学基金委员会、中国地质学会工程地质专业委员会、中国岩石力学与工程学会、国际工程地质与环境协会、国际岩石力学与岩石工程学会的支持!感谢绍兴文理学院、中国地质大学(武汉)、中国科学院地质与地球物理研究所、中国电建成都勘测设计院、华东勘测设计院的长期支持!也感谢华北水利电力大学为承办第五届谷德振讲座做出的努力!
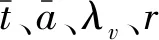
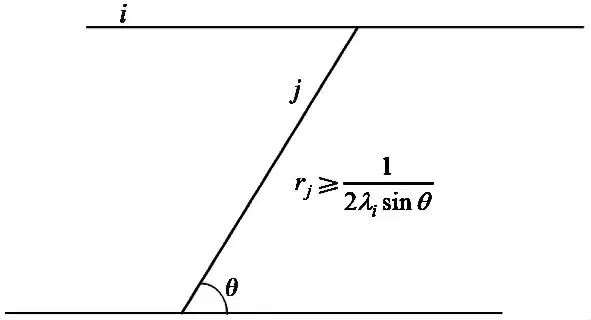
2.4 统计岩体力学原理的几个重要应用
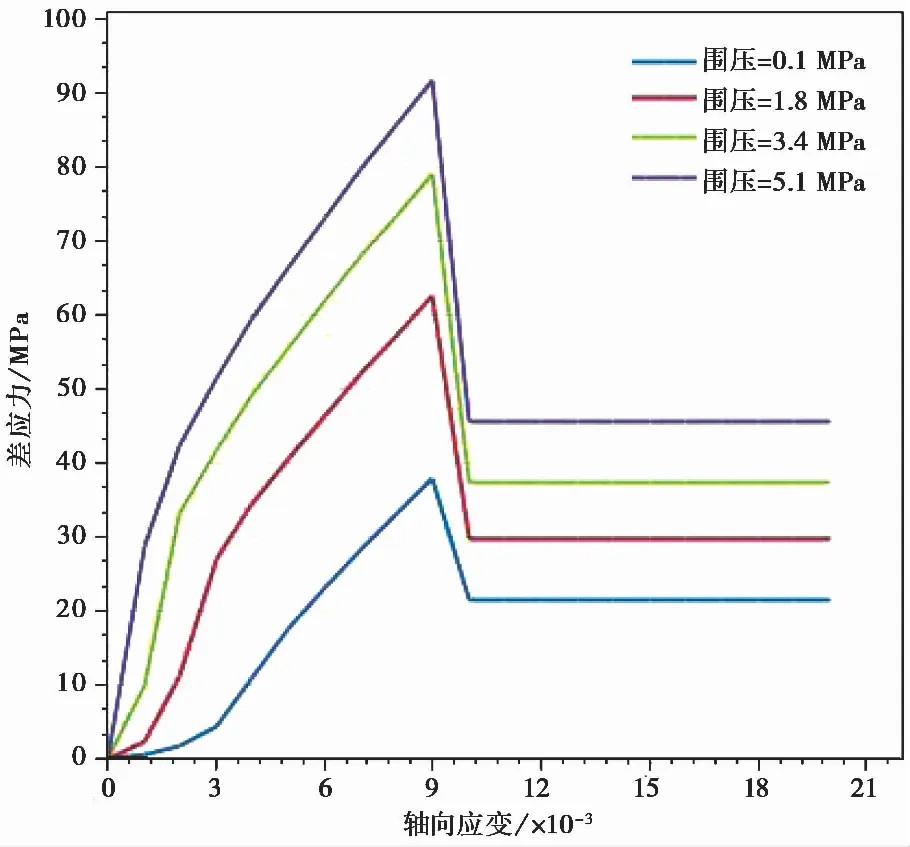
3 统计岩体力学的应用技术

3.1 岩体数据的现场采集技术

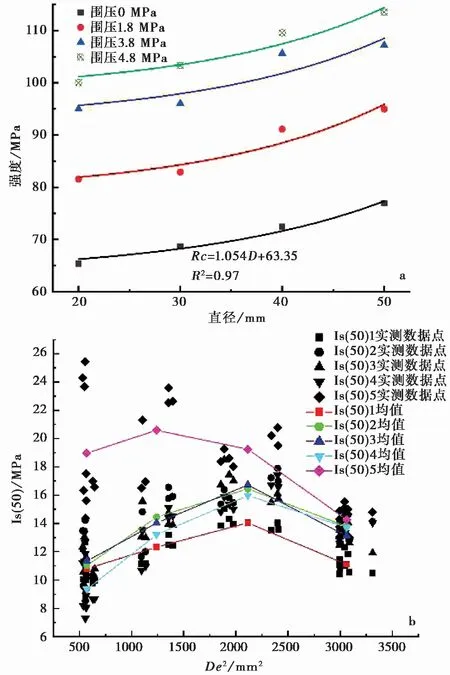
3.2 岩体结构参数计算
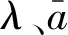
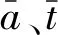

3.3 岩体变形参数计算

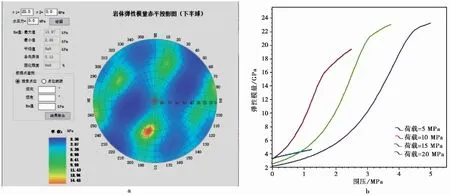
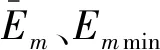
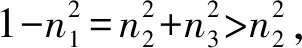
3.4 岩体抗压强度与抗剪强度计算
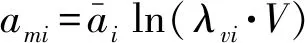

3.5 岩体渗透系数计算
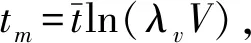
3.6 各向异性岩体质量分级
3.7 工程岩体主动加固
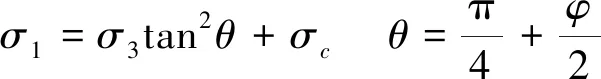

3.8 岩体工程参数云计算系统
4 结 论

