干湿循环与初始静偏应力耦合作用下城市污泥固化土动力累积变形特性*
杨爱武 袁腾云 杨少朋 张 卫
(①东华大学环境科学与工程学院, 上海 201620, 中国) (②天津城建大学天津市软土特性与工程环境重点实验室, 天津 300384, 中国)
0 引 言
随着经济的快速发展,城市污泥增加所带来的处理问题常使人诟病,采用污泥固化技术不仅能有效处理污泥(郑修军等, 2008; 李磊等, 2009; 杨爱武等, 2018),还可以将其作为城市主干道、机场跑道等的路基填料。这一处理方式符合我国的环保理念,因此研究城市污泥固化土的动力特性显得尤为重要。
目前,国内外许多学者考虑初始静偏应力或动应力对土体动力特性的影响进行了大量的研究,硕果累累。如Tan et al. (1989)指出黏土在循环荷载作用下,初始静偏应力与土体动强度成正比关系; France et al. (1977)与Ansal et al. (1989)对土体在动力作用下的动强度与动应力幅值和振次的关系进行了研究,确定了动应力幅值存在临界值; 陈成等(2017)通过对泥炭质土在循环荷载作用下的试验,表明了大动应力幅值和静偏应力会加剧土的累积塑性变形; 张勇等(2009)研究发现饱和重塑软黏土在循环荷载作用下的累积塑性应变发展可以用稳定型、破坏型和临界型来描述; 杨爱武等(2017a)考虑动应力与静偏应力等因素,建立了软黏土累积塑性应变的增长模型; 臧濛等(2017)认为静偏应力对结构性黏土的临界动应力和动强度的影响存在分界值; 尹松等(2017)对压实残积土在循环荷载作用下的动力特性进行研究,分析认为当累积塑性应变达到一定值时,变形随动应力幅值的增大而增加,但最终达到稳定状态; 黄茂松等(2006)研究了动偏应力、初始静偏应力和循环周次对上海地区典型饱和软黏土累积塑性变形的影响。然而考虑干湿循环对土体动力特性影响的研究相对较少,但也取得了一些成就。如刘森峙等(2018)提出动应变一定时,干湿循环的次数越多,土体的强度就越低; 龙安发等(2019)通过对红黏土在干湿循环和周期振动荷载作用下的研究,得到了其动应力-应变关系具有明显的非线性关系,且表现为强硬化型; 陈乐求等(2017)研究表明随着干湿循环作用次数增加,土体的动强度会有所衰减,但衰减到一定程度后逐渐趋于稳定; 刘文化等(2015)提出干湿循环会提高土体的临界循环动应力以及动强度。
以上研究围绕干湿循环作用、初始静偏应力和循环荷载作用3个因素对土体的动力特性进行研究,研究对象大多数是软黏土及粗粒土,而对于城市污泥固化土并且同时考虑这3个因素对其动力特性影响的研究却很少。因此开展此方面的研究具有非常重要的现实意义,可为循环荷载作用下污泥固化土的长期变形控制提供理论依据和借鉴。
1 试验方案
试验采用海积软黏土作为骨架,其基本物性指标如表 1所示。

表 1 天津滨海软黏土基本物性指标Table 1 Basic physical properties of Tianjin Binhai soft clay

表 2 城市污泥固化土的制备方案Table 2 Preparation of municipal sludge solidified soil
1. 污泥与干土的质量比之和为100%; 2. 生石灰的质量按与污泥质量百分比添加; 3. 水的质量按与污泥和干土总质量的百分比添加; 4. 固化剂主剂和辅剂的质量按与污泥、干土和水总质量的百分比添加
试验采用自主研发的固化剂(专利申请号: 201610286857.3),主要由固化剂主剂水泥和固化剂辅剂A、B两部分组成。按照正交试验确定的最佳配比方案制样,城市污泥固化土试样的制备方案如表 2所示,具体步骤如下。
首先,需要提前对原始的污泥用生石灰及少量氢氧化钠进行有机质与含水率的消减处理,然后称取一定质量的干土、消减处理的污泥与水按比例混合充分搅拌,然后添加固化剂,搅拌均匀(图 1a),再将其注入事先准备好的模具中,为了防止水分流失,将模具上下口用透气不透水的土工布包裹并用胶带进行密封,PVC管模具内壁事先涂上一层凡士林,以方便日后脱模取样,最后将试样密封放在恒温恒湿环境下养护。试样成型后(图 1b)脱膜放入密封的塑料袋中,贴好标签,放入标准养护室(温度为(20±2)℃,相对湿度在95%以上)继续养护以达到所需的龄期。

图 1 制样及样品图Fig. 1 Sample preparation and sample drawing
试样经标准养护28d后进行干湿循环试验,具体步骤为:首先,将不同干湿循环次数试样摆好顺序放入烘箱中低温干化12h(保持(35+3)℃),取出称重,之后每隔1h称重一次,直至质量变化小于1%(李磊等, 2009; 何中江等, 2018); 然后,将试样在常温下(20℃左右)放置1~2h,随后用保鲜薄膜将试样四周包紧,放在透水石之上,并连同透水石一起放入定制的模具中,向模具中注水至水没过试样底部少许为止,静置(图 2),试样将由于其孔隙的毛细作用而吸水,当土样上表面完全湿润后,再将试样取出,置于(20+3)℃的培养箱中湿化24h,取出称重,之后每隔1h称重一次,直至质量变化小于1%; 最后,取出去膜,清理干净试样,室温下放置1h; 此为一个循环。

图 2 湿化试验Fig. 2 Humidity test
图3为不同初始静偏应力作用下城市污泥固化土三轴剪切峰值强度与干湿循环次数的关系曲线。
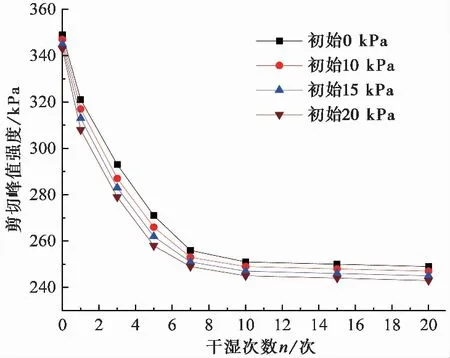
图 3 三轴剪切峰值强度与干湿循环次数关系Fig. 3 The relationship between the peak strength of triaxial shear and the number of dry wet cycles
从图 3可以看出,城市污泥固化土峰值强度随干湿循环次数的增加整体呈现先减小后逐渐稳定的趋势,且各初始荷载作用下变化趋势基本相同。前5次干湿循环过程中强度衰减很大,占15次干湿循环后强度衰减量的70%以上; 循环次数超过5次之后,强度衰减量随干湿循环次数增加而逐渐减小,在7次之后趋于平稳, 10次干湿循环之后强度基本稳定,不再受干湿循环的影响。因此,选择0次、1次、3次、5次、7次、10次干湿循环作为影响次数研究较为合适。
试验仪器选用DDS动三轴仪。由于污泥固化土作为路基填料时,多受地震、交通荷载等循环作用的影响,根据黄博等(2011)的总结,循环荷载的动力波频率范围为0.1~10Hz,以1~2Hz为主,因此选择频率为1Hz的正弦波来模拟城市污泥固化土循环加载方式; 考虑到实际工程中污泥固化土路基填料厚度,选择围压20kPa来模拟填筑1m的路基; 由于路基填料处于干燥非饱和状态,故试验条件为不固结不排水; 动应力幅值的选取参考三轴剪切试验时城市污泥固化土的峰值破坏强度(图 3)。本试验以加载30000次时,轴向应变未达到5%为判停标准,否则以轴向应变5%为停止标准。具体试验方案如表 3和表 4所示。

表 3 动三轴试验方案Table 3 Dynamic triaxial test scheme
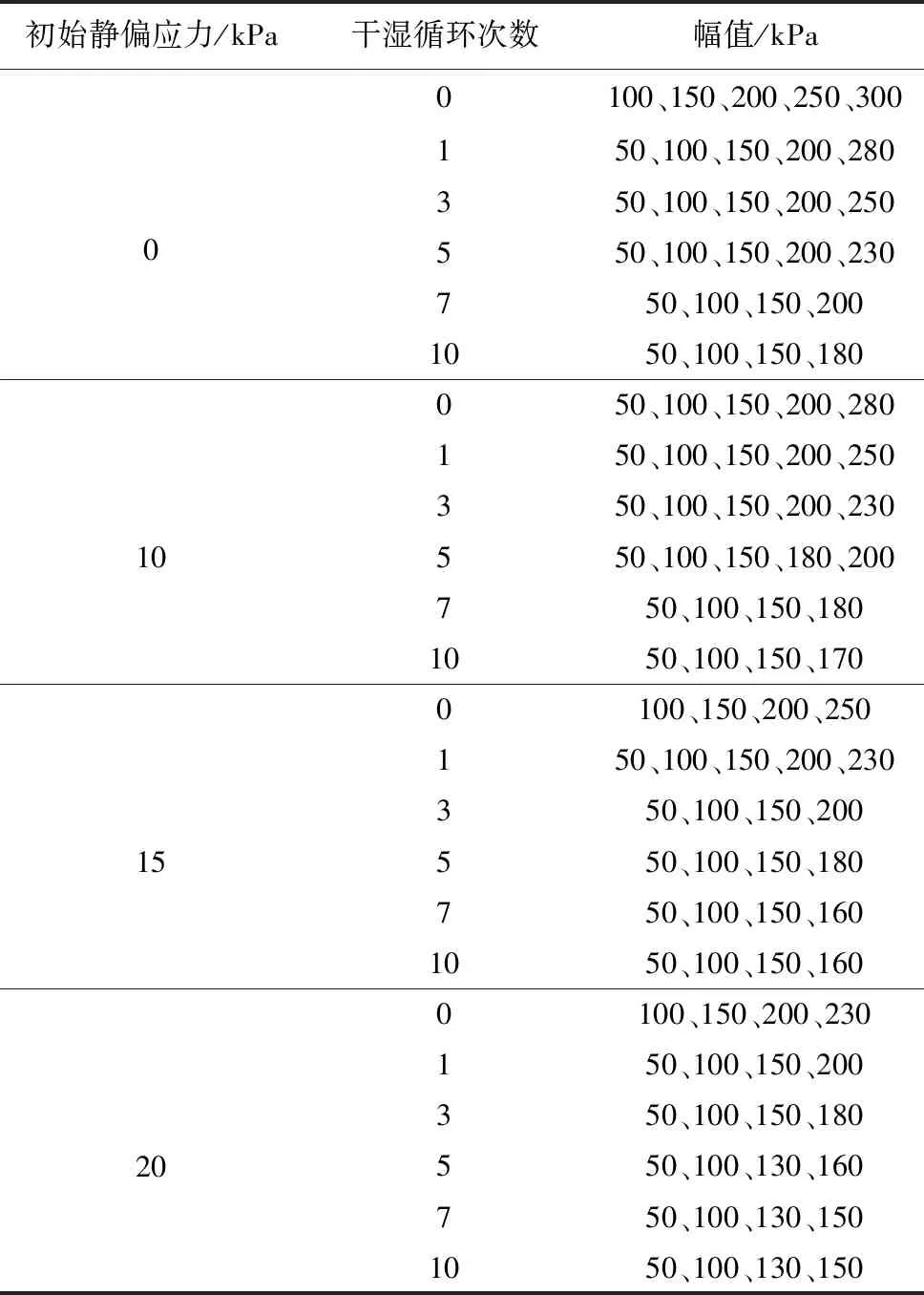
表 4 动应力加载方案Table 4 Dynamic stress loading scheme
2 试验成果与分析
2.1 累积塑性应变分析
图 4至图 7为城市污泥固化土在不同初始静偏应力及干湿循环次数下累积塑性应变随循环振次变化的曲线。限于篇幅,图中干湿循环次数仅选择1、3、7和10。
由图 4至图 7可以看出,干湿循环单独作用下,总体上表现为土体累积塑性应变会随着干湿次数的增加而增大,达到一定次数后,则趋于稳定。但与初始静偏应力耦合作用下对土体累积塑性应变的影响不太显著。动应力对土体累积塑性应变的影响较大,且存在临界值:当动应力小于临界值时,累积塑性应变随着动应力的增大而增大,随着循环振次的增加,最终趋于平稳,变形曲线为硬化型; 当动应力大于临界值时,累积塑性应变在达到某一振次后快速增大,土体迅速产生变形破坏。
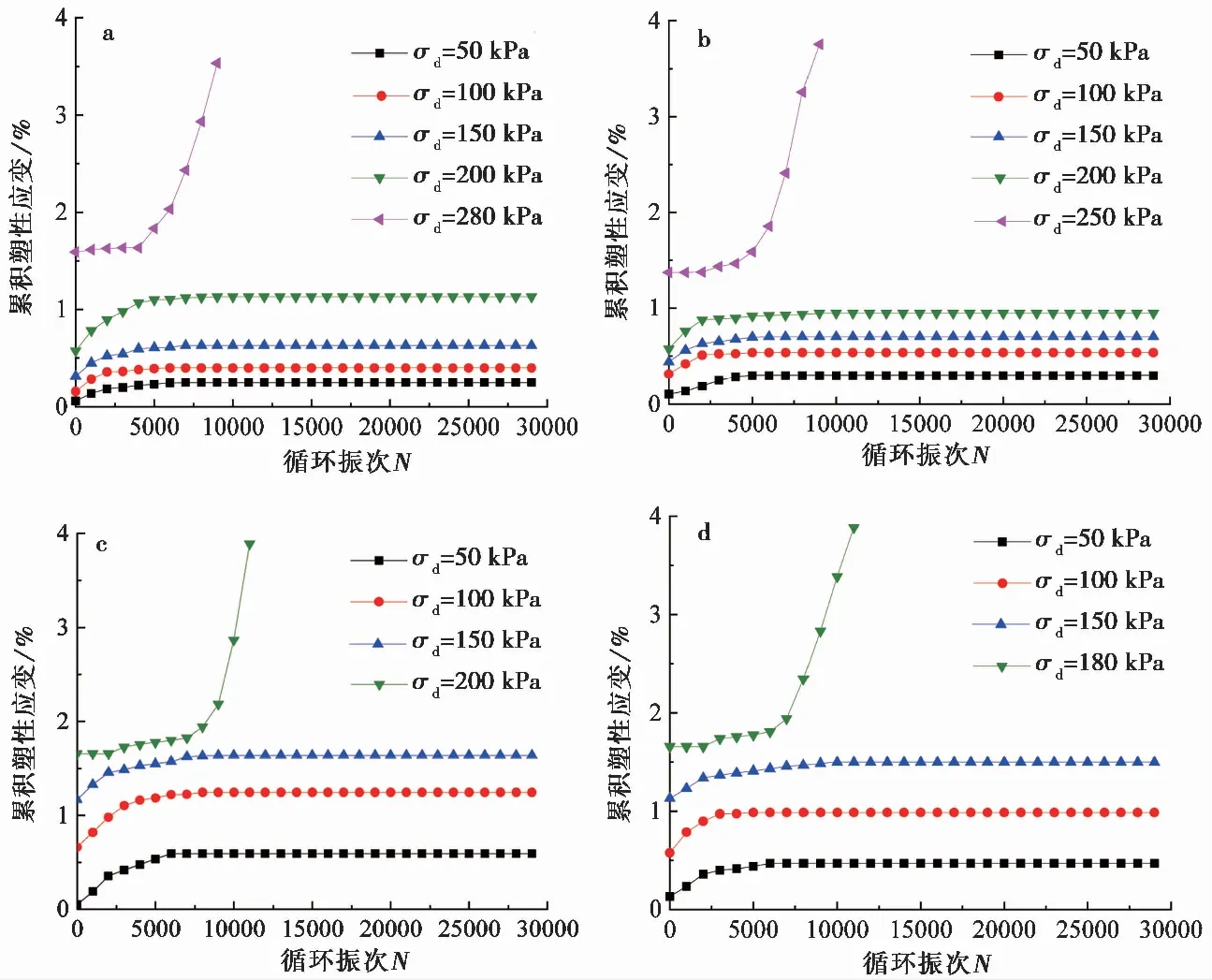
图 4 初始静偏应力0kPa不同干湿次数下累积塑性应变曲线Fig. 4 Cumulative plastic strain curve under initial static deviatoric stress of 0kPa at different dry and wet timesa. n=1; b. n=3; c. n=7; d. n=10

图 5 初始静偏应力10kPa不同干湿次数下累积塑性应变曲线Fig. 5 Cumulative plastic strain curve under initial static deviatoric stress of 10kPa at different dry and wet timesa. n=1; b. n=3; c. n=7; d. n=10
产生上述现象主要与土体结构破损有关。单一干湿循环作用会对土颗粒间的联结造成损伤,破坏土体结构,但其破坏程度有限,多次干湿循环后,颗粒联结趋于稳态,土体结构稳定,因此土体累积塑性应变呈现出先增大后稳定的趋势。与初始静偏应力耦合作用时,由于初始静偏应力的施加,使得土颗粒间的接触更为紧密,在一定程度上因干湿循环作用所造成的颗粒联结破损又重新挤密联结,土体抵抗变形能力变化不大,并且所施加的初始静偏应力远小于土体的结构屈服应力,故宏观上干湿循环与初始静偏应力耦合作用下对土体累积塑性应变的影响不太显著。动应力对土体结构的破坏较严重,大大降低了土体抵抗变形的能力,使得土体变形增大。当动应力小于临界值时,随着动应力的增加,土中孔隙数量减少,气体被压缩,孔隙中的细微颗粒发生位移,土体产生不可恢复的塑形变形,即累积塑性应变不断增大; 动应力继续增加,土体结构继续破坏,破损颗粒数量增多,随着循环振次的增加,颗粒继续滑移且重新分布,形成“饱和”稳定状态,其宏观表现为累积塑性应变的增长逐渐趋于稳定; 当动应力大于临界值时,伴随循环振次的增加,土体结构在某一瞬间“分崩瓦解”,即颗粒分布“饱和”稳定状态被破坏,大颗粒破碎成小颗粒,颗粒之间产生剧烈滑动,且动应力越大,破碎与滑动越快,土体结构损坏也越严重,其宏观表现为累积塑性应变不断增大。
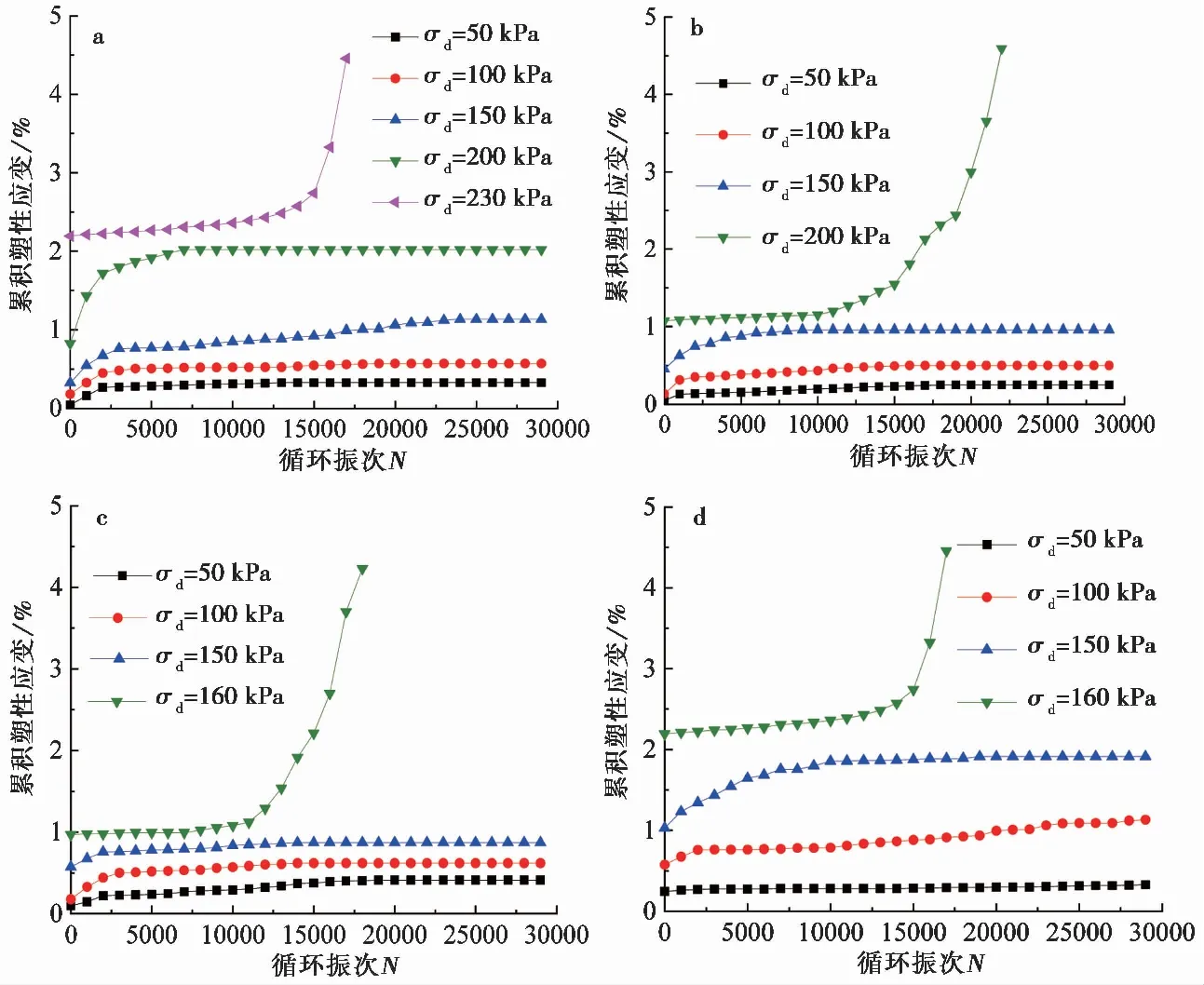
图 6 初始静偏应力15kPa不同干湿次数下累积塑性应变曲线Fig. 6 Cumulative plastic strain curve under initial static deviatoric stress of 15kPa at different dry and wet timesa. n=1; b. n=3; c. n=7; d. n=10

图 7 初始静偏应力20kPa不同干湿次数下累积塑性应变曲线Fig. 7 Cumulative plastic strain curve under initial static deviatoric stress of 20kPa at different dry and wet timesa. n=1; b. n=3; c. n=7; d. n=10
2.2 动强度特性
图8为不同初始静偏应力下城市污泥固化土动强度随干湿循环次数变化的曲线。

图 8 不同干湿循环次数下动强度曲线Fig. 8 Dynamic strength curve under different dry and wet cycles
由图 8可见,相同初始静偏应力下,城市污泥固化土的动强度随着干湿循环次数的增加先逐渐减小后逐渐趋于稳定。同一干湿循环次数下,随着初始静偏应力的增大,城市污泥固化土的动强度在逐渐降低。
究其原因,城市污泥固化土的强度主要来源于土颗粒间复杂联结所形成的黏结力以及颗粒间相互咬合与滑动所产生的摩擦力,并且城市污泥固化土中的固化剂、土颗粒和水之间会发生一系列水化反应,生成大量胶结物质,这些胶结物质不仅有效增强了土颗粒间的联结,而且改变了土颗粒间原有的接触和排列方式,使得颗粒间的“自锁”作用与咬合能力增大,从而提高了城市污泥固化土的强度。土的动强度是指在一定振次的动荷载作用下达到破坏标准所需的动应力(谢定义, 2011; 陈强等, 2019; 庄心善等, 2020),即动强度的大小与选择的破坏标准有关。一般来说,土体的强度越大,其对应的动强度也相对较大。城市污泥固化土在经过前几次干湿循环后,发生失水干缩与吸水湿胀等现象,内部出现了裂缝,水过多地进入裂缝,使胶结物质部分软化,从而降低了土体的黏结力和摩擦力,其宏观表现为土体的动强度明显下降; 但在经过更多次的干湿循环后,土体中发生失水干缩与吸水湿胀等现象不再明显,裂缝不再继续扩大,胶结物质的软化达到稳定状态,动强度也就逐渐趋于稳定。初始静偏应力会加速胶结物质的破损,降低土颗粒之间的黏结力和咬合力,而且增加越大,胶结物质破损越多,其宏观表现为城市污泥固化土的动强度越来越低。
3 累积塑性应变模型建立及参数确定
3.1 累积塑性应变模型建立
结合以往学者(Monismith et al.,1975)的研究成果,通过对图 4~图 7的试验结果进行分析,发现可采用式(1)描述城市污泥固化土稳定型累积塑性应变与循环振次的关系。
(1)
式中:N为循环振次;a、b、c为与应力条件和土的性质有关的参数。现从动应力、干湿循环次数和初始静偏应力3方面对式(1)中参数进行确定。
3.2 动应力的影响
为方便分析,采用式(1)对图 2的累积塑性应变曲线进行计算,可得到如表 5所示的相关参数。
用式(1)分析,当循环振次N趋于无穷大时,对函数取极限,可得累积塑性应变εP近似等于参数c,c具有累积塑性应变极限值的物理意义。因此,c值逐渐增大的规律正好符合动应力越大、土样所产生的累积塑性应变越大的客观事实。
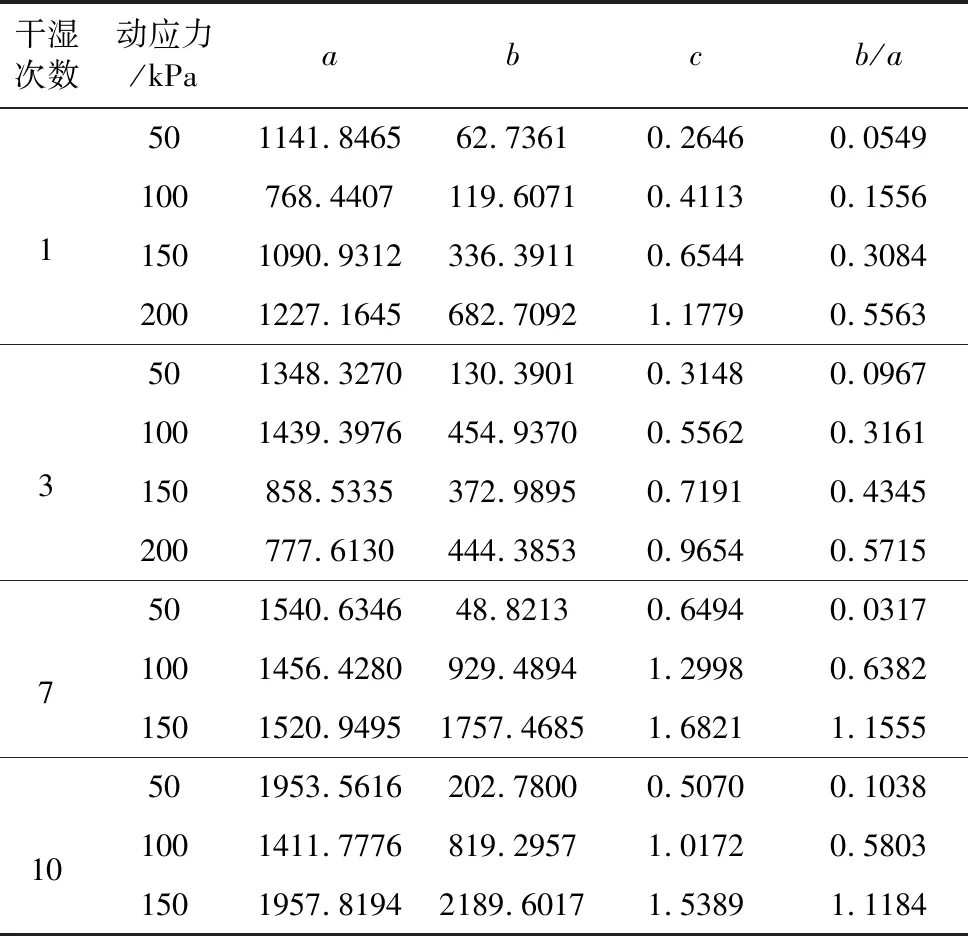
表 5 初始静偏应力0 kPa累积塑性应变参数取值Table 5 Values of cumulative plastic strain parameters of initial static deviator stress 0 kPa
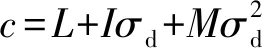

表 6 不同干湿次数方程中参数取值Table 6 Parameter values in the equation under different times of drying and wetting
3.3 干湿循环次数的影响
由于动应力小于临界值时,随着动应力的增加,土样所产生的累积塑性应变随之增大,大于临界值时,土样在一定循环振次下发生破坏。为此假定参数c取到最大值时所对应的动应力是临界动应力σcr,对图 4~图7进行分析,发现临界动应力σcr会随着干湿循环次数的增大而降低。根据不同干湿循环次数n与临界动应力σcr的值,利用式(2)进行描述:
σcr=-10.01469n+245.30248
(2)
令Rσ=σd/σcr,其取值区间为(0,1),Rσ称为相对动应力比。将临界动应力作为归一化因子,得到不同干湿循环次数下参数b/a、c、b与相对动应力比Rσ之间的关系曲线,如图 9所示。
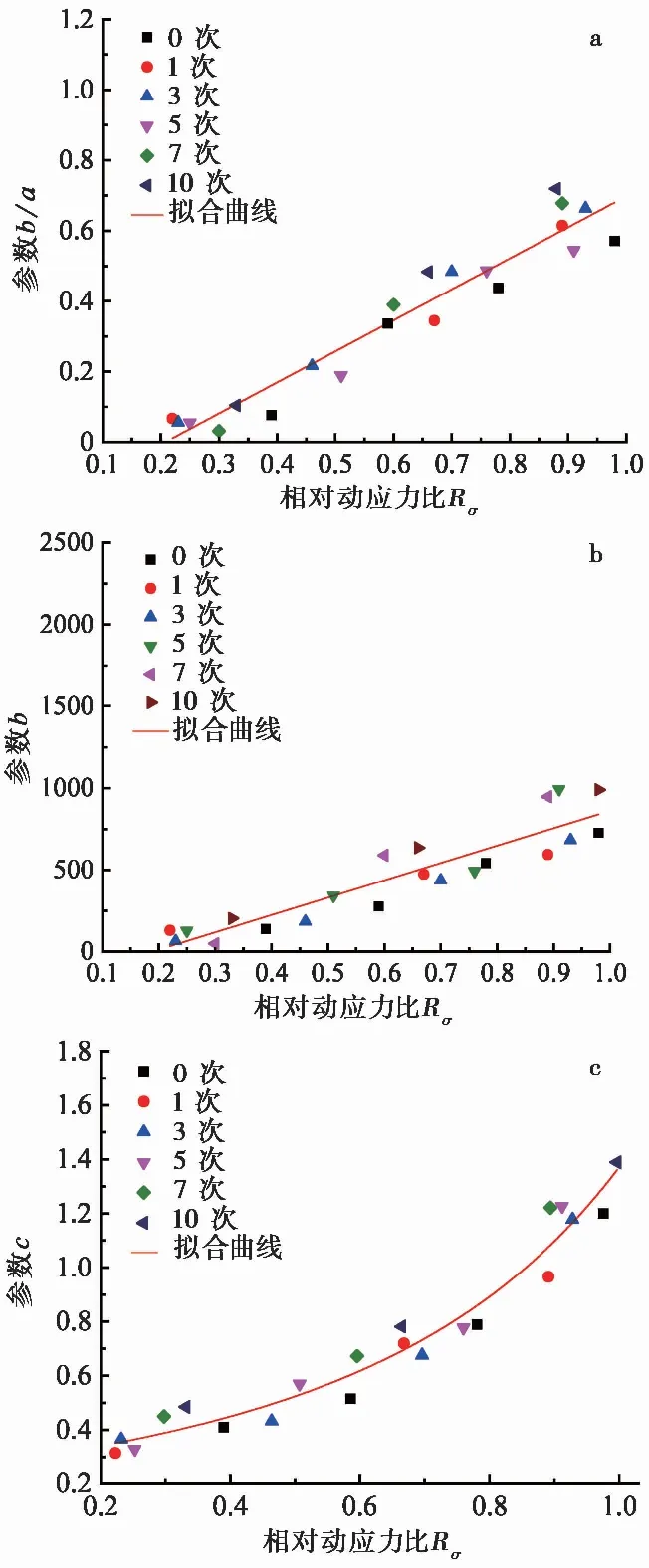
图 9 参数与相对动应力比关系Fig. 9 Relation between parameters and relative dynamic stress ratio
根据图 9,通过回归分析,可建立参数b/a、b、c与相对动应力比Rσ之间的关系,具体如下:
b=1061.84002Rσ-200.81374
(3)
(4)
b/a=0.88119Rσ-0.18325
(5)
3.4 初始静偏应力的影响
为便于分析,本文选取干湿循环为3次,采用式(1)计算图 5~图 7不同初始静偏应力下累积塑性应变曲线,可得计算参数如表 7所示。

表 7 不同初始静偏应力下参数取值Table 7 Parameter values under different initial static deflection stresses
设Q=q/n(q为初始静偏应力,n为干湿次数),动应力相同时,假定无初始静偏应力时的参数a为a0、b为b0、c为c0,有初始静偏应力时的参数b与b0的比值(b/b0)称为相对b值,参数c与c0的比值(c/c0)称为相对c值,参数b/a与b0/a0的比值(ba0/ab0)称为相对b/a值。得到不同初始静偏应力下b/b0、c/c0、ba0/ab0与Q的关系曲线,如图 10所示。
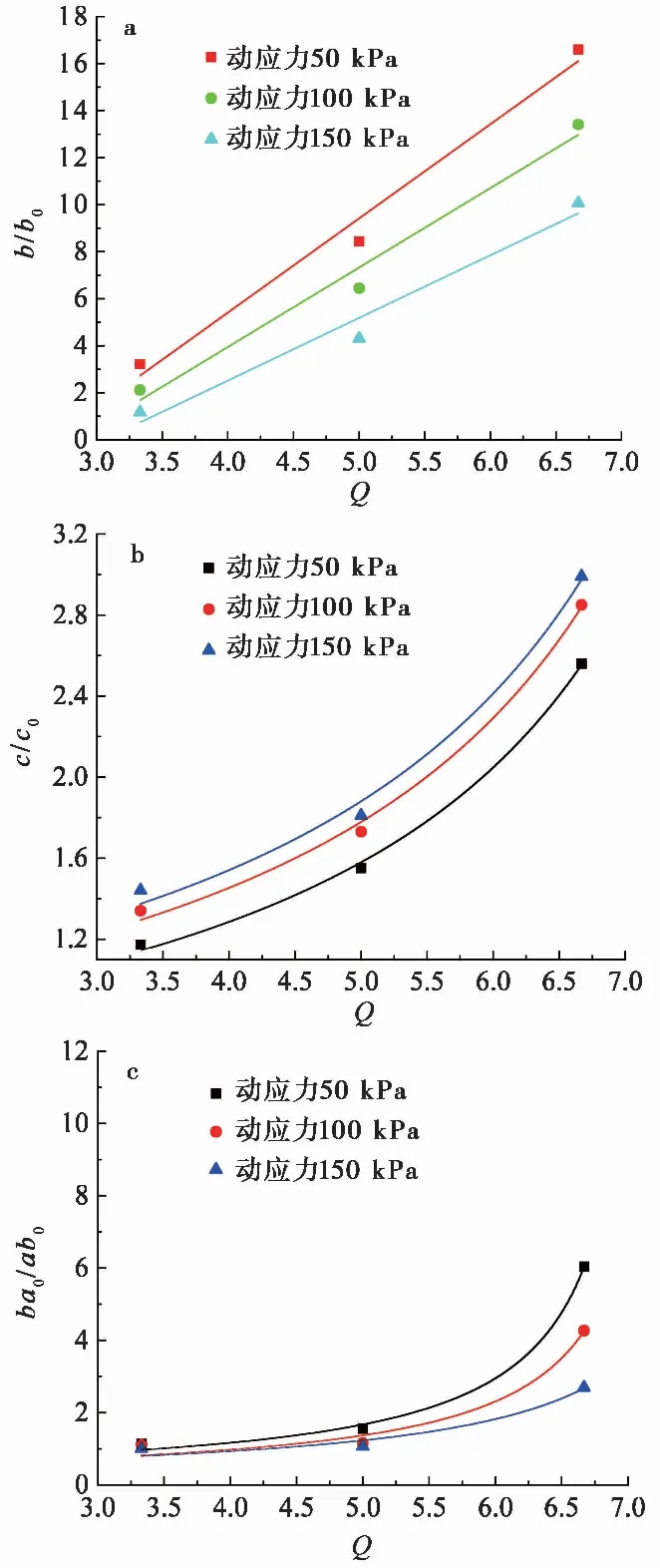
图 10 b/b0、c/c0、ba0/ab0与Q关系Fig. 10 Relation between b/b0,c/c0,ba0/ab0 and Q
由图 10的关系曲线可以得到如下方程:
ba0/ab0=1/2.07491-0.27238q/n
(6)
b/b0=3.3503q/n-9.44261
(7)
c/c0=1/1.22256-0.12934q/n
(8)
将式(2)~式(8)及表 5~表 7的数据代入式(1),并对龄期为28d的城市污泥固化土,在围压为30kPa、初始静偏应力为15kPa及干湿循环为5次条件下的累积塑性变形曲线进行验证,试验结果与计算结果如图 11所示。

图 11 累积塑性变形曲线验证效果图Fig. 11 Cumulative plastic deformation curve verification renderings
由图 11可以看出,本文给出的稳定型累积塑性变形预测公式基本可以描述在其他稳定型动荷载作用下,累积塑性应变与初始静偏应力、干湿循环次数及循环振次之间的变化关系。
4 结 论
(1)干湿循环单独作用下,土体累积塑性应变随其增加而先增大后趋于稳定,但与初始静偏应力耦合作用下对土体累积塑性应变的影响不太显著,动应力对其影响较大,且存在临界值:当动应力小于临界值时,累积塑性应变呈现出先增大后逐渐稳定的趋势; 当动应力大于临界值时,累积塑性应变在达到某一振次后快速增大,土体迅速产生变形破坏。
(2)干湿循环与初始静偏应力都会降低土体的动强度,但干湿循环在达到10次后,动强度将趋于平稳,不再受其影响。
(3)根据稳定型累积塑性应变曲线发展特点,通过回归分析,考虑干湿循环次数、初始静偏应力及动应力等因素的影响,建立了城市污泥固化土稳定型累积塑性应变模型,并验证了其可行性。

