基于WPA优化LSSVM的输电线路覆冰厚度预测

汪 晗，李启迪，黄治翰，刘 闯

(1.国网鄂州供电公司，湖北 鄂州 436000；2.国网荆门供电公司，湖北 荆门 448000)

随着全球能源互联网概念的提出，大容量远距离输电成为未来输电线路的发展方向[1]。目前，超、特高压输电线路基本采用架空线，由于架空输电线路直接暴露在外部环境中，当温度、湿度和风速满足一定条件时，在其表面容易形成覆冰，严重时能引起导线舞动，甚至发生断线、倒塔等事故，造成大面积停电[2-3]。因此，建立精度更高的输电线路覆冰厚度预测模型，准确预测覆冰厚度便于及时采取相应措施保障系统安全稳定运行。

自2008年我国南方冰灾事故后，覆冰厚度预测方法研究引起了专家学者们的广泛关注[4]，目前也取得了一些研究成果。陈勇等人对微气象数据进行了主成分分析(principal component analysis，PCA)，并用遗传算法(genetic algorithm，GA)对最小二乘支持向量机(least squares support vector machine，LSSVM)进行参数寻优，建立了基于PCA-GA-LSSVM的输电线路覆冰负荷在线预测模型，实现了输电线路覆冰负荷在线预测，但模型的应用效果有待进一步验证[5]。庄文兵等人认为建立覆冰厚度预测模型应考虑时间累积效应，因此建立了考虑气象因素和时间累积效应的覆冰厚度预测模型，并利用支持向量机(support vector machine，SVM)对覆冰厚度进行预测，但预测精度有待提高[6]。刘闯等人采用扩展记忆粒子群算法(particle swarm optimization with extended memory，PSOEM)对LSSVM参数进行优化，建立了基于PSOEM-LSSVM的输电线路覆冰厚度预测模型，但PSOEM优化效果不够理想[7]。

针对现有输电线路覆冰厚度预测方法上存在的不足，本文采用优化性能更好的狼群算法(wolf pack algorithm，WPA)对LSSVM的惩罚因子和核函数参数进行优化，建立了基于WPA优化LSSVM的输电线路覆冰厚度预测模型，实现小样本覆冰数据精确拟合，提高输电线路覆冰厚度预测精度，并采用算例分析验证该方法的正确性和模型实用性。

1 算法概述

1.1 最小二乘支持向量机

LSSVM是Suykens基于SVM提出的一种改进方法，与SVM具有相同的核函数，LSSVM回归过程中同样遵循结构风险最小化原则。LSSVM与SVM不同点在于优化指标和约束条件，LSSVM优化指标采用平方项，约束条件采用等式约束，在不影响回归精度的情况下大大减少了计算量。LSSVM结构简单，非常适合小样本预测，在交通、金融和电力行业应用广泛，LSSVM回归的原理及步骤可参考文献[8]。为了提高输电线路覆冰厚度预测精度，本文采用高斯径向基核函数(radial basis function，RBF)作为LSSVM回归拟合时的核函数。

研究表明，惩罚因子C和核函数参数σ直接影响LSSVM的回归拟合效果，C控制样本的惩罚程度，σ影响核函数的泛化能力，C和σ的合理取值是建立输电线路覆冰厚度预测模型的关键。

1.2 狼群算法

WPA由吴虎胜等于2013年提出，是一种求解精度更高的寻优算法[9]。WPA原理是模拟群狼捕食猎物获得最优解，把狼群分为头狼、探狼和猛狼，头狼指挥，探狼搜寻猎物，猛狼攻击猎物，各狼职责如图1所示。狼群算法定义如下。

a.设置狼群中狼的数量为N，预寻优变量的数量为D，则狼的状态为Xi=(xi1,xi2,…,xiD)。

b.生成头狼，即寻找初始解中的最优解Ylead。头狼不是固定的，在迭代计算的过程中，所有狼的位置都会不断更新，如果出现比头狼更好的解则替换。

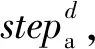
(1)

此时计算新的新适应度值Yip，如果比前适应度Yi更好则替代，并将探狼的位置Xi更新，然后比较探狼的新适应度与头狼适应度Ylead，如果优于Ylead，则用探狼代替头狼，并召唤猛狼来当前位置，否则继续寻优，一直到最大迭代次数Tmax。

d.猛狼奔袭。猛狼是指除去上述2种狼的剩余部分，其个数为N-M，猛狼收到头狼召唤后，立即奔向头狼，猛狼奔袭的步长为N-M，d维中猛狼第k+1次迭代位置为

(2)

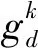
猛狼奔袭后的适应度为Yi，如果Yi优于Ylead，则该猛狼变为头狼，并召唤其他猛狼过来，否则猛狼继续向头狼奔袭，直到距离头狼的位置小于dnear时，开始攻击猎物。

(3)

式中:ω为判定因子;(mind,maxd)为d维变量的取值范围。

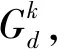
(4)

式中:λ为随机数，λ∈[-1,1]。

围攻猎物时狼群位置的适应度优于原来的适应度，则替换更新，否则不变。

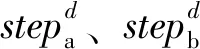
(5)

式中：S为步长因子。

f.狼群更新。在搜索猎物的过程中，会淘汰适应度最差的R匹狼，并随机产生R匹狼予以补充，R由[N/2×β,N/β]确定，β为更新比例因子。

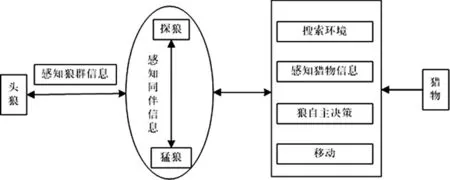
图1 狼群中各狼的职责

2 输电线路覆冰厚度预测模型

输电线路覆冰是一种复杂的自然现象，覆冰厚度变化受温度、风速和湿度等多种因素影响，因此研究覆冰厚度与影响因素之间的函数关系，建立相应的预测模型，可以指导线路运维工作。具体建模步骤如下。

a.获得覆冰历史数据并将其归一化。

(6)

式中：xi为原始特征量；xmax为原始特征量最大值；xmin为原始特征量最小值；x′i为归一化后的特征量。

b.将原始覆冰数据分为训练集和测试集，训练集用于覆冰厚度预测模型训练，测试集用于检验模型的预测精度。

c.设置LSSVM的惩罚参数C、核函数参数σ的初始值，令C=100、σ2=2.5，本文将覆冰厚度预测结果的均方根误差作为适应度值。

(7)

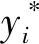
d.设置WPA相关参数，设狼的数量N为100，探狼比例因子α为4，步长因子S为800，距离判定因子ω为600，最大迭代次数kmax为100，探狼游走最大次数Tmax为20，游走方向h为4，更新比例因子β为5。

e.执行迭代。利用WPA对LSSVM的C和σ2进行寻优，每执行1次迭代，将C和σ2的值代入LSSVM中训练1次，并计算训练后模型的适应度值(均方根误差)，比较并判断是否满足迭代终止条件，若满足则输出最优参数，否则继续迭代。

f.当均方根误差达到最小或迭代次数达到最大，则将最优参数赋给LSSVM模型，即可对测试集数据进行预测。

结合上述步骤可以得到WPA优化LSSVM的输电线路覆冰厚度预测流程，如图2所示。

3 算例分析

表1给出了2015年西南地区某500 kV输电线路一次覆冰增长过程的气象数据和覆冰厚度，本文根据时间顺序对36组数据进行编号，编号为1-36，前30组数据为训练集，后6组为测试集。在MATLAB软件中计算分析，以温度、风速和湿度为支持向量，覆冰厚度为输出值，建立WPA-LSSVM覆冰厚度预测模型，对训练集数据进行训练，WPA迭代寻优过程如图3所示。

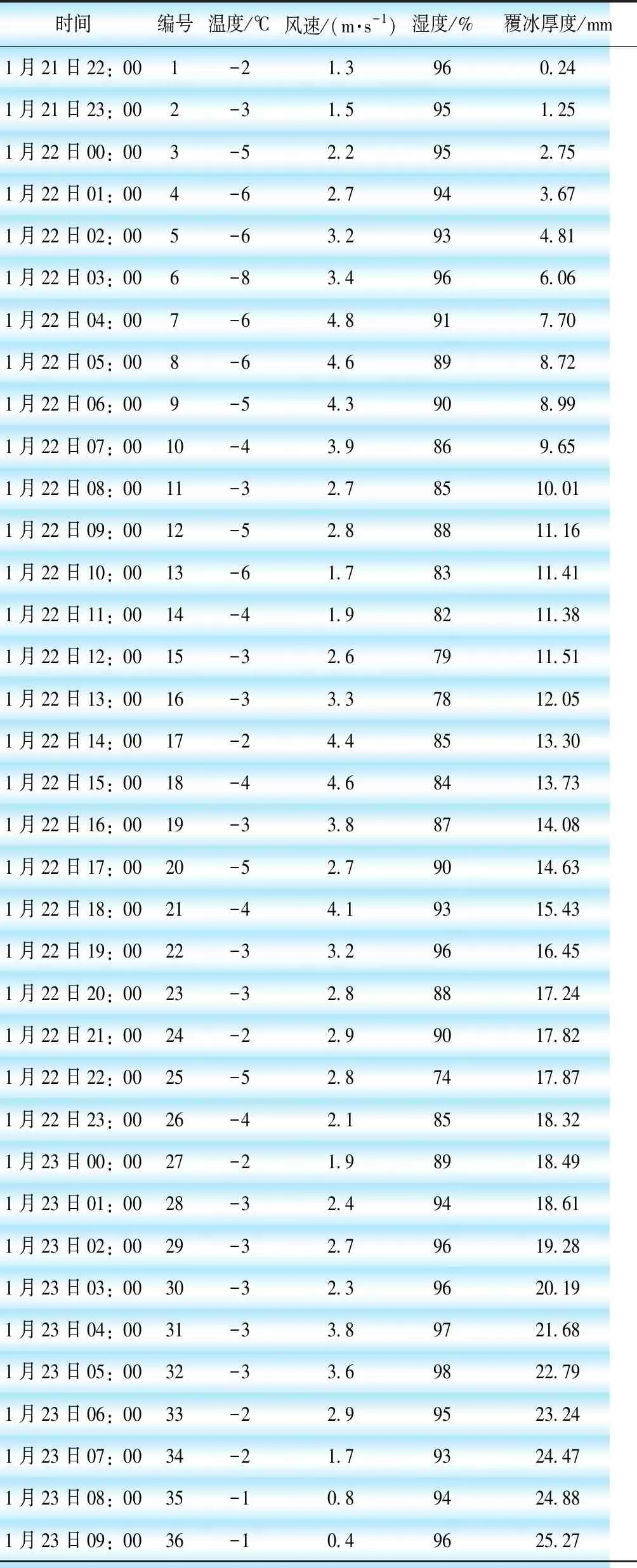
表1 某500 kV输电线路覆冰监测数据

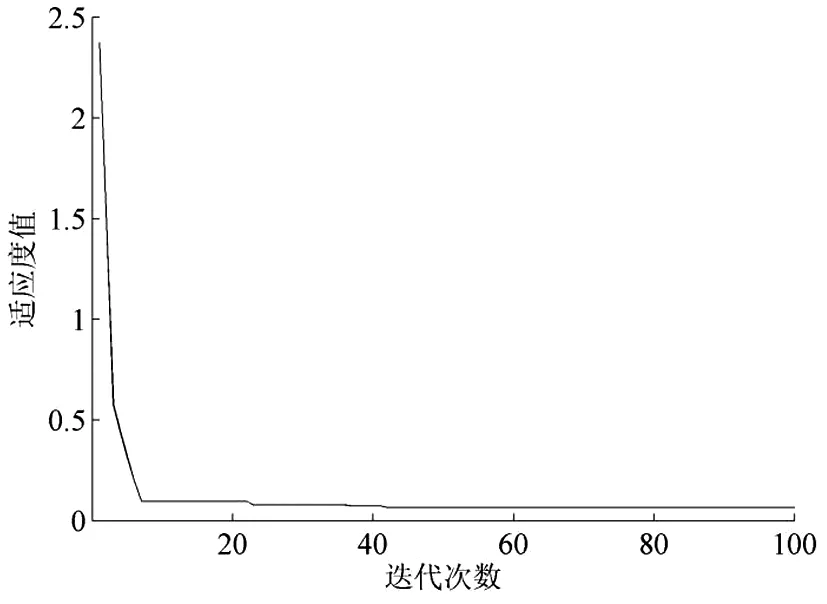
图3 WPA迭代寻优过程

由图3可知，WPA经过42次迭代后找到全局最优解，即C=64.48和σ2=2.65。

为了对比WPA-LSSVM模型的预测效果，分别采用相同数据建立GA-BP、PSO-LSSVM覆冰厚度预测模型，3种模型训练效果如图4所示。

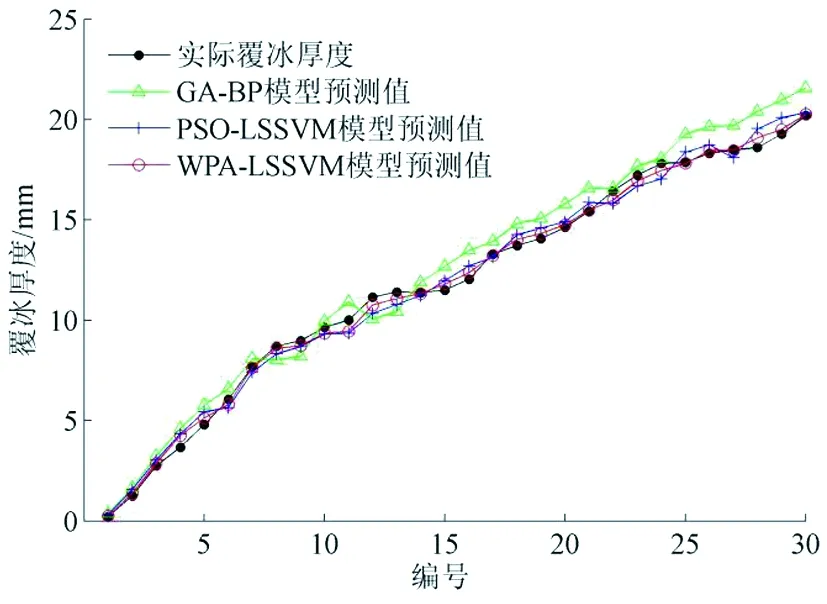
图4 3种模型训练效果

由图4可知，WPA-LSSVM模型的训练效果优于其他2种模型，其拟合效果更接近输电线路覆冰厚度实际增长趋势。3种模型的训练误差如图5所示。

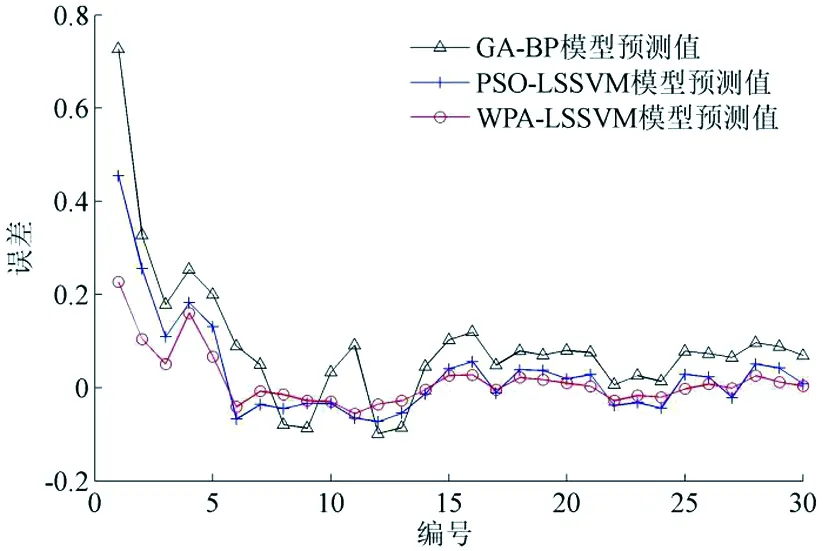
图5 3种模型训练误差

由图5可知，WPA-LSSVM模型在训练过程中的误差波动更小，训练效果更好。采用3种模型对训练好的测试集中的6组覆冰厚度进行预测，预测结果如图6所示。

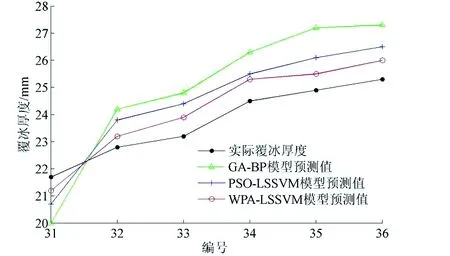
图6 测试集数据预测结果

由图6可知，对比其他2种模型，WPA-LSSVM模型对测试集预测效果更好。

采用均方根误差、平均相对误差和全局最大相对误差作为输电线路覆冰厚度预测模型的评价指标，均方根误差已在式(7)中给出，平均相对误差和全局最大相对误差分别为

(8)

(9)

表2给出了GA-BP、PSO-LSSVM和WPA-LSSVM 3种模型对测试集数据预测结果的误差。

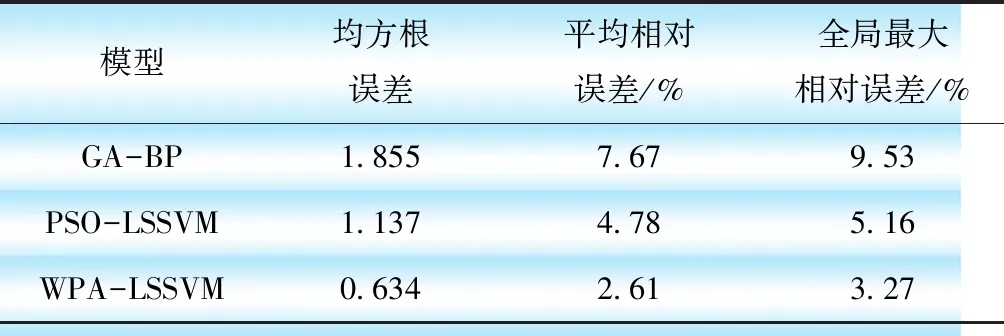
表2 3种模型预测结果误差

由表2可知，WPA-LSSVM模型的均方根误差、平均相对误差和全局最大相对误差分别为0.634、2.61%和3.27%，相比于其他2种模型误差明显减小，该预测方法能够减小覆冰厚度预测过程中的数据波动，进一步提高覆冰厚度预测精度。

4 结语

本文采用WPA对LSSVM的惩罚因子和核函数参数进行优化，建立了基于WPA优化LSSVM的输电线路覆冰厚度预测模型，采用某500 kV输电线路实际覆冰数据对模型的正确性和实用性进行了验证。仿真结果验证了基于WPA优化LSSVM的输电线路覆冰厚度预测方法能够减小覆冰预测过程中的数据波动，进一步提高覆冰厚度预测精度，为输电线路覆冰厚度预测提供了一种新方法。