考虑冲击力的球轴承复合缺陷动力学建模

李志农， 周泽文， 胡茑庆， 程 哲， 胡 蛟

(1. 南昌航空大学 无损检测技术教育部重点实验室， 南昌 330063； 2. 国防科技大学 装备综合保障技术重点实验室， 长沙 410072)

以上研究聚焦于轴承的单一缺陷，而滚动体通过缺陷产生的冲击和磨损会诱发多点缺陷，造成内外圈均存在缺陷的情况，复合缺陷问题得到了学者们的关注.李志农等[9]将VMD算法与平行因子分析相结合，对轴承复合故障信号实现了更为有效的盲源分离；Patel等[10]提出了深沟球轴承动力学模型，研究了轴承内圈和外圈存在单点和多点缺陷时的振动响应；朱永生等[11]建立了6自由度动力学模型，研究复合缺陷下的动力学响应，涉及外圈和基座的振动传递，并引入Lempel-Ziv指标进行量化评价；王凯等[12]提出了4自由度复合缺陷深沟球轴承动力学模型，并对工况和尺寸参数的影响进行了分析；胡爱军等[13]针对轴承外圈上多处剥落产生的复杂振动响应，分析总结了轴承故障特征随故障数量、间隔的变化规律，对轴承多点故障的诊断提供了理论依据.目前考虑冲击力的复合缺陷模型还较为罕见，模型精度需要进一步提高.

本文考虑轴承内圈和外圈各两个自由度，基于赫兹接触理论建立了4自由度的轴承模型；通过将剥落缺陷简化为滚道中的矩形坑，在模型中嵌入缺陷参数；针对滚动体通过剥落缺陷的过程，考虑所引起的时变位移激励，引入了离开缺陷区域时，滚动体撞击剥落后边沿所产生的冲击力，并分析其作用角度；分别模拟了轴承外圈、内圈单一缺陷和内外圈各有一剥落缺陷时的振动响应，通过与实验数据的对比验证了模型的有效性，并探究负载、缺陷尺寸对系统振动特性的影响，分析结果对于研究球轴承复合缺陷下振动机理具有一定的理论价值.

1 复合缺陷轴承动力学建模

图1 球轴承弹簧质量模型

1.1 运动分析及接触力计算

滚动体和滚道之间的等效接触刚度为

(1)

式中，ki和ko分别为滚动体与内外滚道的接触刚度.对于深沟球轴承，n取1.5.

所建立的深沟球轴承模型主要承受径向负载，由于滚动体与内外滚道之间游隙的存在，以及滚动体承载数目的周期性变化，轴承会产生变刚度振动，引起水平x、竖直y方向上的位移，x、y正方向如图1所示，并规定角度方向由y轴正向开始，逆时针为正.保持架的速度为

(2)

式中：Db和Dp分别为滚动体直径和轴承节圆直径；α为接触角；ω为内圈和转轴的角频率.忽略滚珠的自转，滚动体在保持架的带动下间隔相等角度转动，第j个滚动体在t时刻转动的角度为

分析： 综合以上分析，为避免水稻品种抗病性丧失过快，一方面可以丰富水稻的抗病品质，即具有R1R2R3，以应对拥有不同A基因的MP；另一方面，可以在同一区域分别种植抗病和感病水稻，以弱化对MP的选择作用，避免A基因频率的过快变化。

(3)

式中，N为球轴承滚动体个数.进而可以得到第j个滚动体在θj处的径向变形量为

δj=Xsinθj+Ycosθj-0.5Cr

(4)

式中：X和Y分别为轴承在水平和竖直方向的位移量；Cr为轴承的径向游隙.根据赫兹接触理论，可将接触力分解到x和y方向上，即

(5)

式中，γj为定义的赫兹接触开关函数，表示只有当滚珠与滚道之间存在弹性变形时才会产生赫兹接触力，其表达式为

(6)

1.2 缺陷引起的时变位移激励

首先考虑内滚道或外滚道上单一缺陷的情形，当滚珠通过滚道上的剥落缺陷时，会产生随时间变化的径向偏移，使滚动体与滚道的接触变形量发生变化，导致接触力的变化，激发周期性振动.假设滚动体直径大于缺陷宽度，且缺陷深度足够大，使得滚动体不与缺陷底部接触，即4Dbh≥4h2+L2，式中，h和L分别为缺陷的深度和宽度.缺陷区域引起的额外位移δd在滚珠越过剥落前边沿之后产生，而后逐渐增大，滚动体与滚道的接触形变随之减少，接触力减小，在滚动体运动到缺陷中心位置时，额外位移达到最大值δdmax，而后随着滚动体接触剥落后边沿，额外位移开始减小，弹性变形随之增大，赫兹接触力也逐渐恢复正常接触水平.因此，可采用半正弦函数来模拟δd随时间的变化，以外滚道缺陷为例，如图2所示，可以得出缺陷导致的最大额外变形量为

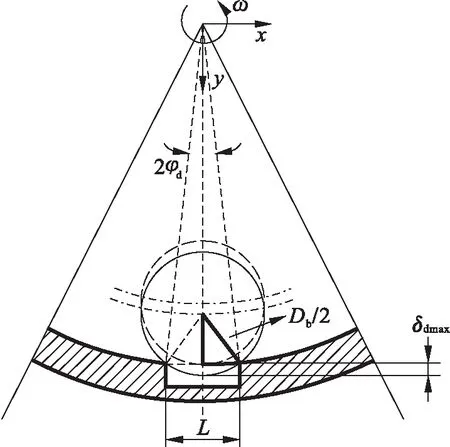
图2 滚动体与外圈缺陷接触示意图

(7)

定义缺陷区域开关函数βo，以判断滚珠是否处于外圈缺陷区域，其表达式为

(8)

式中：φo为外圈缺陷中心所对应的角度(本文角度值定义为转角对2π求余所得)；φd为缺陷宽度对应的圆心角的一半，其表达式为

(9)

可得滚珠通过外圈缺陷所产生的额外位移量为

(10)

δj=Xsinθj+Ycosθj-0.5Cr-δdo

(11)

当内圈存在剥落缺陷时，最大变形量计算与外圈情况相似，但需要注意内圈随轴转动，缺陷位置是时变的，可表示为

φi=φi0+ωt

(12)

式中，φi0为内圈缺陷的初位置.类比外圈缺陷的情况，可以定义相对应的内圈开关函数βi，并得出内圈缺陷引起的额外变形量，即

(13)

进一步修正接触变形量的计算公式为

δj=Xsinθj+Ycosθj-0.5Cr-δdo-δdi

(14)

1.3 考虑冲击力的时变接触力激励

在研究滚动体通过剥落缺陷区域导致的时变接触力时，除了考虑上述的额外位移量对赫兹接触力的影响，还应将滚动体碰撞剥落后边沿的冲击力计入其中.结合上文对滚动体在缺陷区域的运动描述，在滚动体质心到达缺陷中心线的瞬时时刻，额外位移达到最大，而同一瞬时滚动体也在保持架的带动下撞击剥落后边沿，产生脉冲响应，诱发轴承各部件的高频振动，因而在动力学模型中考虑冲击力的影响是非常必要的.

在滚动体经过缺陷区域时，滚道与滚动体的接触力先减小，当滚动体与前后边沿均接触的瞬时达到最小，同时碰撞剥落后边沿，产生附加的撞击力fimp，随后滚动体逐渐退出剥落区，冲击引起的额外接触力又逐渐减小，在滚动体完全离开剥落后，接触力恢复正常，短暂间隔后下一个滚动体到达剥落前沿，循环往复上述过程.以内圈为例，采用分段函数的形式表示时变接触力，其表达式为

(15)

式中，fmin和fmax分别为接触力变化的最小、最大绝对值，两者之和即为冲击力fimp.文献[8]对其大小进行了计算，即

(16)

式中：fr为径向载荷；C为与冲击材料有关的常量.图3为滚动体撞击剥落后边沿示意图.根据图3所示的几何关系，可将冲击力分解到x、y方向上，即

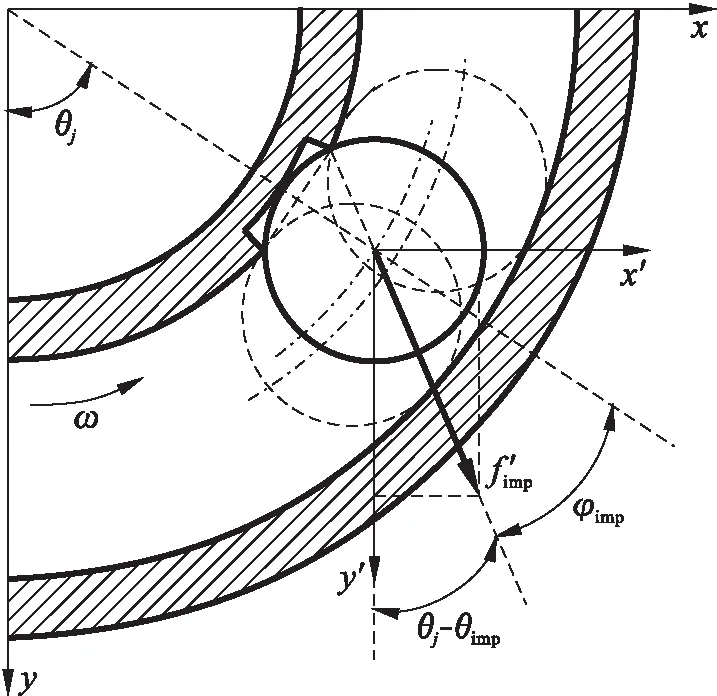
图3 滚动体撞击剥落后边沿示意图

(17)

式中：fdix和fdiy分别为内滚道存在缺陷时的冲击接触力在水平和竖直方向的分量；φimp为冲击角，φimp=arcsin(L/Db).

当外圈存在剥落缺陷时，类比内圈缺陷的情况，可以定义相对应的时变接触力fdo，同样将其分解到x、y方向上，需要注意其冲击力的作用角度与内圈存在缺陷时不同，即

(18)

式中，fdox和fdoy分别为外滚道存在缺陷时的冲击接触力在水平和竖直方向的分量.

1.4 内外圈复合缺陷模型

针对轴承的多个部件上出现缺陷的情况，基于图1模型的假设，结合以上对单一缺陷模式的分析计算，设定内外圈分别具有一处剥落缺陷，且缺陷宽度相同，并模拟轴承制造或与轴的配合安装误差等因素所产生的离心力，建立考虑冲击力的内外圈复合缺陷动力学微分方程组，即

(19)

式中：mi、ci、mo、co分别为内圈与轴的总质量、内圈与轴间的连接阻尼、外圈与轴承座的总质量、外圈和轴承基座固定的连接阻尼；e、g分别为偏心距和重力加速度.

2 模型求解验证及对比分析

2.1 条件设定

仿真轴承选用MB ER-10K型号，几何参数及转速为1 498 r/min(转频为24.85 Hz)时的故障特征频率如表1所示.将x、y方向上的初始位移设定为10-9m，初速度设定为0，步长设定为10-6s，仿真时长t=5 s，内圈与轴的阻尼ci和外圈与轴承座的连接阻尼co分别为2 276 N·s/m和1 210 N·s/m，径向载荷fr=70 N，安装偏心距e=10-6m，缺陷宽度L=1 mm.

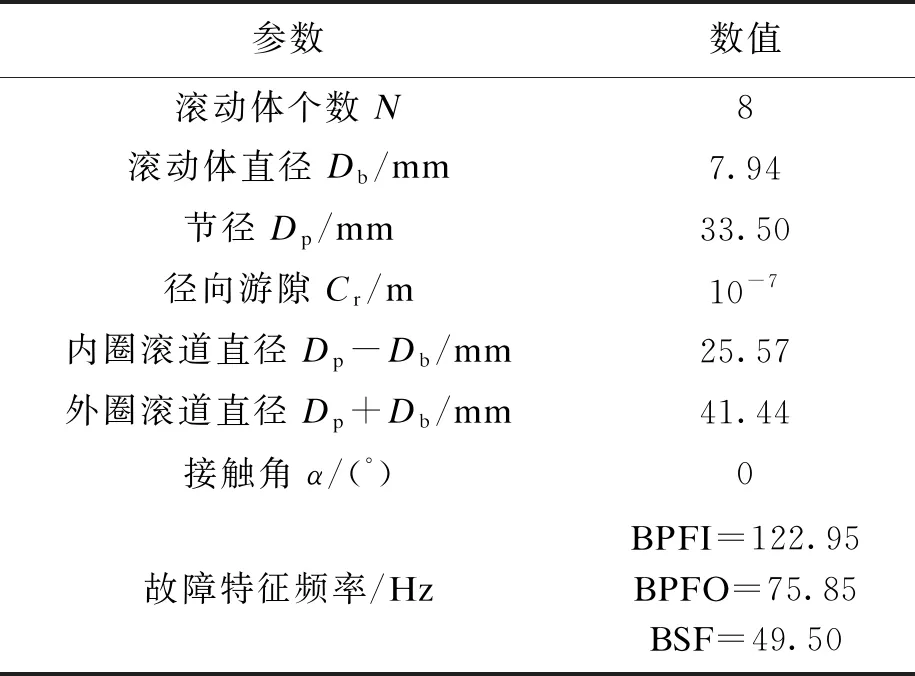
表1 实验轴承参数

2.2 内圈和外圈单一缺陷模型

基于以上参数设定，对于仅内圈滚道存在一剥落缺陷时，解得的仿真时域波形和包络谱如图4所示.

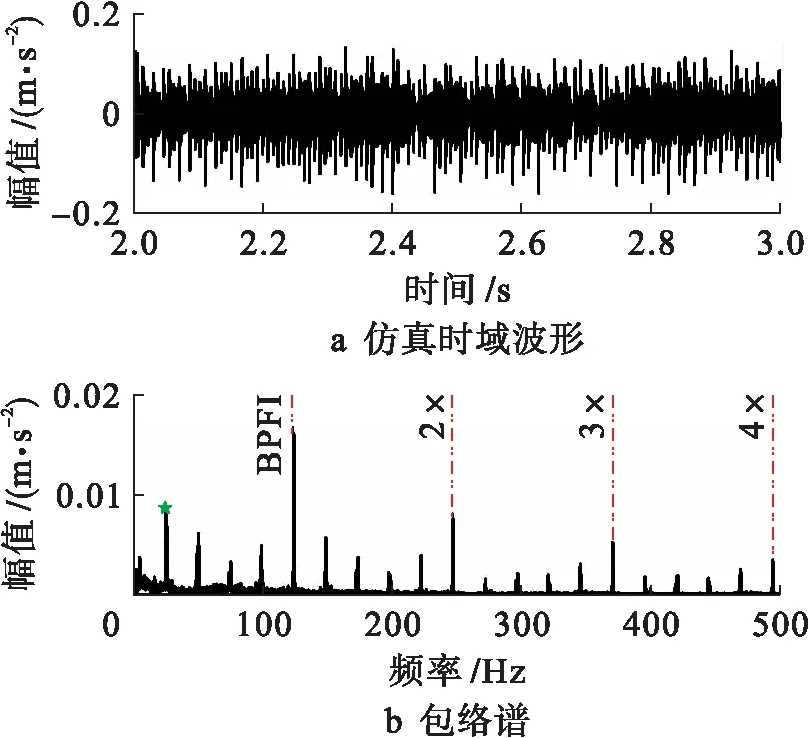
图4 内圈含单一缺陷球轴承的仿真时域波形和包络谱

内圈上的剥落缺陷位置会随轴一起转动，造成每个冲击的幅值具有一定差异，反映在时域波形中为一系列幅值大小不等的冲击振动，包络谱图中的转频(24.85 Hz)和内圈故障频率(BPFI=122.95 Hz)及其倍频(49.7、245.88、368.82 Hz)处皆有明显峰值，并且以内圈故障频率为中心，带宽为转频的边频带清晰可见，说明了该模型的正确性.在相同转速下，外圈滚道单一缺陷情况的仿真时域波形及包络谱如图5所示.为验证模型的正确性，以同型号轴承外圈剥落缺陷为例，在SpectraQuest机械故障仿真实验台上进行实验探究，拾取到的加速度时域波形及其包络谱如图6所示.

图5 外圈含单一缺陷球轴承的仿真时域波形和包络谱

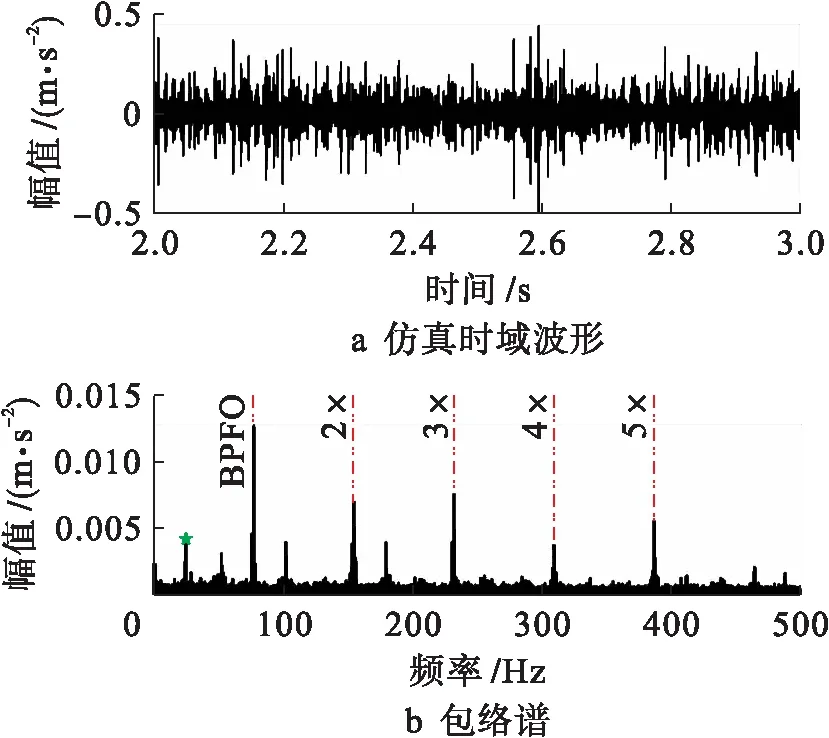
图6 外圈含单一缺陷球轴承的实测时域波形和包络谱

将仿真数据与实验数据进行对比发现，外圈缺陷的包络谱图形均表现为一系列以外圈故障特征频率为间隔的随频率增大、幅值逐渐减小的离散谱线，并且外圈故障频率(BPFO=75.85 Hz)及其倍频(151.7 Hz、227.55 Hz等)处皆有明显峰值，和转频调制生成的边频带清晰可见，幅值差异在误差允许范围内，故所建立模型可以较好地模拟单一缺陷下的振动响应.

2.3 内外圈复合缺陷模型

同样设定条件下，对内外圈各含有一单点剥落缺陷的复合缺陷模型进行求解.仿真时域波形和包络谱如图7～8所示，相比于单一缺陷情形，由于多缺陷的耦合作用，复合缺陷下时域波形中冲击幅值相对增大，而且更加不易看出周期性特征，从刚度损失的角度可以解释为复合缺陷导致轴承接触刚度发生更大变化，使得动力学性能改变，同时包络谱中的主要频率成分和调制产生的边频带也变得更为复杂.

图7 复合缺陷球轴承的仿真时域波形

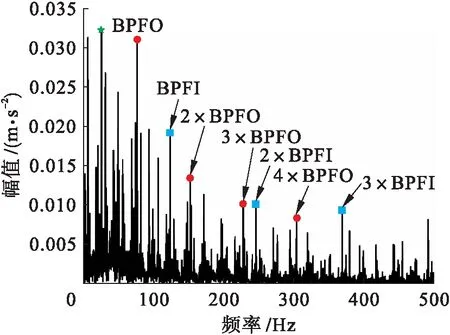
图8 复合缺陷球轴承的仿真包络谱

图9～10为实测复合缺陷轴承的时域波形及包络谱.由于条件限制，实验所用轴承还存在滚动体缺陷.将实测数据和仿真数据对比可以发现，仿真数据的时域波形较好地模拟了复合缺陷下的振动冲击特征，在包络谱中可以观察到内、外圈故障频率及其倍频处有明显尖峰，在其周围可发现以转频为带宽的边频带，以及与实测信号相似的丰富边频带信息，说明了内外圈复合缺陷模型的合理性.计算结果表明，滚动轴承的复合缺陷具有相互耦合、抑制、强度不平衡的特点，还表明从包络谱中提取的倍频分量可以作为识别复合缺陷的有效依据.

图9 复合缺陷球轴承的实测时域波形

图10 复合缺陷球轴承的实测包络谱

2.4 负载和缺陷尺寸影响

针对复合缺陷轴承承受60、70、80 N径向负载的情况，分别进行仿真求解和包络谱分析，取转频及其二倍频、BPFO、2×BPFO、BPFI、2×BPFI等典型频率处对应的包络谱幅值来说明负载大小对其振动特征的影响，如图11所示.可以发现，总体上振动幅值随径向负载的增加而增大，在BPFO及2×BPFO处幅值有明显增加，负载的变化对外圈故障频率的影响相较于转频及内圈故障频率处更为显著.

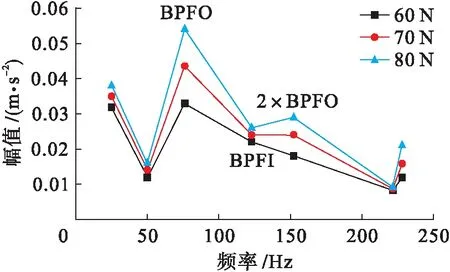
图11 径向负载对球轴承振动幅值的影响

对复合缺陷轴承在0.8、1.0、1.2 mm三种不同缺陷宽度下的振动响应进行仿真，不同缺陷宽度下的频谱幅值变化如图12所示.根据前一节对冲击力的描述可知，冲击力会随着故障宽度加长而增大，从图12中可以发现，随着L的增大，转频及其二倍频、BPFI处的幅值都有明显增加，符合滚动轴承损伤演化的规律.

图12 缺陷宽度对球轴承振动幅值的影响

3 结 论

本文基于赫兹理论，考虑滚动体在缺陷区时变位移激励，描述并分析了滚动体退出剥落时撞击后边沿所致的冲击力作用机理，采用半正弦函数模拟了滚动体在缺陷区域的动力学行为，并考虑安装偏心距，建立了4自由度的内外圈复合缺陷球轴承动力学模型.分别对内圈、外圈单一缺陷和复合缺陷的情况进行数值求解，对得到的仿真信号进行包络谱分析，其包络谱中相应的故障特征频率及边频带清晰可见，与实测数据基本吻合.结果表明，该动力学模型能够有效反映复合缺陷下轴承的振动特征.对不同负载和缺陷宽度的振动响应进行了仿真分析，径向负载的增加和缺陷尺寸增大都会使轴承振动幅值增大，加重轴承的损伤.