高速铁路大跨度连续刚构拱桥吊杆张拉方案研究

傅安民

(中国铁路设计集团有限公司，天津 300308)

引言

大跨度连续刚构拱桥是一种梁式结构和拱式结构的组合结构[1]，是为解决大跨度混凝土桥徐变变形控制难题而出现的桥型。该桥型的结构自重仍由主梁承担，而主跨范围内的二期恒载与活载则由拱肋承担，拱肋的提拉作用可以使结构刚度明显提高，徐变变形得到明显控制。原先由主梁承担的荷载通过吊杆传递给拱肋，故可通过调整吊杆力来改变结构的内力分布，从而优化结构受力[2-3]。对于吊杆张拉施工，需要确定一个合理的吊杆张拉方案，使得在吊杆张拉过程中满足结构的内力、变形及机具承载力的要求，并在吊杆张拉结束后达到目标设计状态[4]。合理的吊杆张拉方案，不仅可使吊杆张拉过程中的结构受力合理，还可使结构的内力和变形过渡平顺，提高张拉过程的安全性[5-6]。

在现有的关于吊杆张拉方案的研究中，多数是对简支梁拱组合体系桥梁的研究[7-12]，鲜有文献对连续刚构拱体系桥梁的吊杆张拉方案进行研究。而简支梁拱桥属于外部静定、内部超静定结构[13]，连续刚构拱桥属于超静定结构，受力更为复杂，且连续刚构拱桥的梁拱刚度比显著大于简支梁拱桥的梁拱刚度比，两种桥型在梁和拱的内力分配上有较大差异，导致吊杆张拉方案对整个结构受力及变形的影响也不同。因此，有必要对连续刚构拱的合理吊杆张拉方案进行研究。以(90+200+90)m钢管混凝土连续刚构拱桥为例，采用桥梁有限元软件MIDAS Civil模拟吊杆张拉过程，提出了5种吊杆张拉顺序，通过吊杆张拉控制力的确定原则确定了相应的吊杆张拉控制力，并对各张拉方案的成桥吊杆力，拱肋混凝土应力，拱肋钢管应力，拱肋位移，拱脚水平推力，主梁应力等进行了对比分析，以寻求使结构受力及变形最合理的吊杆张拉方案，为同类桥型吊杆张拉方案的选择提供参考和借鉴。

1 工程概况

昌景黄铁路义城昌江特大桥主桥为(90+200+90)m预应力混凝土连续刚构与钢管混凝土拱组合结构，在景德镇内跨越昌江。设计速度350 km/h，列车活载为ZK活载，双线线间距5 m，轨道结构形式为CRTS Ⅰ型双块式无砟轨道。采用“先梁后拱”的施工方法，即在主梁挂篮悬臂浇筑施工完成后再进行拱肋的施工。主桥桥型布置如图1所示。

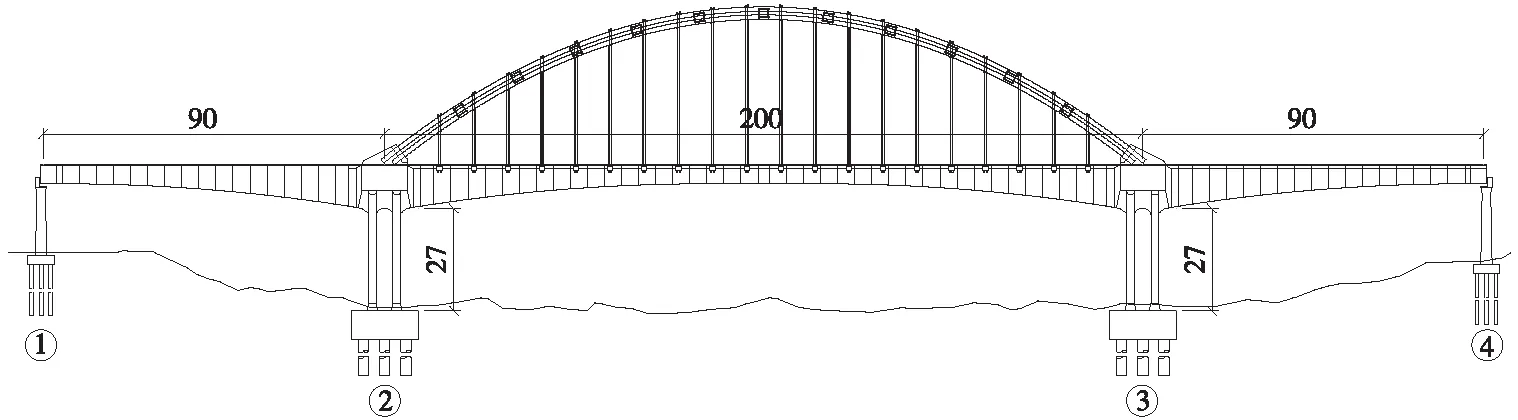
图1 (90+200+90)m连续刚构拱桥立面布置(单位：m)

主梁采用单箱双室、变高度、直腹板箱形截面，中支点处梁高11.5 m，边跨直线段和跨中直线段梁高为5 m，梁底下缘按二次抛物线变化。主墩采用双肢薄壁墩，为普通钢筋混凝土结构，双肢薄壁墩中心间距6.4 m，壁厚2.0 m，墩高均为27 m。拱肋采用竖直平行钢管混凝土哑铃拱，从桥面开始起拱，两拱肋中心距11.9 m，计算跨度为200 m，矢跨比为f/L=1/5，拱肋立面矢高40 m，拱肋采用二次抛物线。拱肋高3.3 m，拱管直径1.2 m。拱肋钢管及腹腔内灌注混凝土。拱肋间设置11道桁架式横撑，横撑为空钢管，内部不填充混凝土。吊杆采用整束挤压钢绞线，吊杆纵向间距9.0 m，共设20对纵向双吊杆。

2 吊杆张拉方案

2.1 吊杆张拉顺序

本桥吊杆布置如图2所示，为减少吊杆张拉顺序的种类，将吊杆按照所处位置进行分区，分为拱脚区、四分区和拱顶区等3块区域[14]。参考文献[14-15]中常用的吊杆张拉顺序，并结合设计经验及结构自身的受力特点，确定了5种典型的吊杆张拉顺序。

图2 (90+200+90)m连续刚构拱吊杆布置(单位：cm)

(1)四分区-拱顶-拱脚交替张拉，即按D5、D10、D3、D6、D9、D2、D7、D8、D1、D4顺序张拉。

(2)拱脚-拱顶-四分区交替张拉，即按D3、D10、D5、D2、D9、D6、D1、D8、D7、D4顺序张拉。

(3)拱脚至拱顶交替张拉，即按D1、D3、D5、D7、D9、D2、D4、D6、D8、D10顺序张拉。

(4)拱顶至拱脚交替张拉，即按D10、D8、D6、D4、D2、D9、D7、D5、D3、D1顺序张拉。

(5)先拱脚-拱顶交替张拉再四分区张拉，即按D1、D10、D2、D9、D3、D8、D4、D7、D5、D6顺序张拉。

以上5种吊杆张拉顺序均采用以中跨跨中为中心，一次对称张拉4组吊杆的方式进行张拉。其中，第2和第4种吊杆张拉顺序分别为第1和第3种吊杆张拉顺序的反向张拉顺序。

2.2 吊杆张拉控制力的确定原则

吊杆张拉方案包括吊杆张拉顺序和吊杆张拉控制力两部分。在对以上5种吊杆张拉顺序确定相应的吊杆张拉控制力时，需要遵循以下几个原则。

(1)安全性[14]。在吊杆张拉过程中，吊杆、拱肋钢管、拱肋混凝土、主梁等结构的应力不应超过规范容许值，如表1所示。

表1 施工阶段结构构件应力容许值

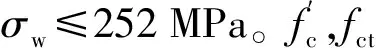
(2)合理性。按吊杆张拉控制力逐个张拉吊杆后的成桥吊杆力应与设计成桥吊杆力尽可能接近，使结构整体受力更合理。

(3)适用性[14]。在吊杆张拉过程中，结构所承受的应力水平及位移宜平缓过渡，避免出现较大的波动。

目前常用的确定施工阶段吊杆张拉控制力的方法有倒拆分析法、正装-倒拆迭代法和影响矩阵法等[5-6，15-17]，当设计成桥吊杆力确定后，根据上述算法，并结合吊杆张拉控制力的确定原则，可以得到5种吊杆张拉顺序对应的吊杆张拉控制力。

3 有限元模拟

采用有限元软件MIDAS Civil 进行模拟计算，全桥共划分为1 893个单元，1 338个节点。对于主梁、桥墩、承台、拱脚、拱肋、横撑的各杆件采用三维梁单元进行模拟。拱轴线为二次抛物线，拱肋采用哑铃形截面，哑铃形钢管内填充混凝土，采用“双单元、共节点”的方法模拟钢管混凝土拱肋。吊杆采用桁架单元模拟，仅考虑其轴向的拉伸刚度。

主梁、拱脚均采用C60混凝土，拱肋混凝土采用C55自密实补偿收缩混凝土，主墩墩顶以下2.2 m范围同主梁一同浇筑，采用C60混凝土，其余部分采用C50混凝土。拱肋钢管、横撑采用Q345qD钢材，吊杆采用整束挤压钢绞线吊杆。主梁、拱肋混凝土、主墩、拱脚、拱肋钢材的容重按结构实际重力进行换算，分别取26.5，24，27，29.1，95.2 kN/m3，弹性模量、泊松比及其余结构的容重均按规范相关要求考虑。

主梁与吊杆之间，拱肋与横撑之间的连接均采用弹性连接中的刚性进行模拟，主梁与主墩之间的连接采用主从节点约束模拟。主墩承台底采用六自由度的节点弹性支承来模拟桩-土相互作用。

通过激活吊杆单元，并施加相应初拉力模拟吊杆的张拉效应[18]，通过主动改变拉力来调整结构的内力分配，使其趋于优化合理[19]。本桥有限元分析模型如图3所示。

图3 有限元分析模型

4 吊杆张拉方案对比分析

本文考虑了5种吊杆张拉方案，以下从施工阶段的成桥吊杆力、拱肋混凝土应力、拱肋钢管应力、拱肋位移、拱脚水平推力、主梁应力等方面对这5种吊杆张拉方案进行对比分析[20]。

4.1 成桥吊杆力对比

利用有限元软件MIDAS Civil 进行正装成桥分析，得到5种吊杆张拉方案的成桥吊杆力，并与设计成桥吊杆力进行对比，结果如表2所示。

表2 成桥吊杆力对比分析 kN

由表2可知，与设计成桥吊杆力相比，方案1：D10成桥吊杆力(229 kN)与设计成桥吊杆力(280 kN)相差最大，误差达18.3%，D4成桥吊杆力(225 kN)与设计成桥吊杆力(224 kN)相差最小，误差为0.3%。方案2：D10成桥吊杆力(220 kN)与设计成桥吊杆力(280 kN)相差最大，误差达21.6%，D4成桥吊杆力与设计成桥吊杆力相差最小，两者几乎一致(均为224 kN)。方案3：的各吊杆成桥吊杆力与设计成桥吊杆力十分接近，误差均在0.2%以内。方案4：D5成桥吊杆力(216 kN)与设计成桥吊杆力(175 kN)相差最大，误差达23.5%，D9成桥吊杆力(267 kN)与设计成桥吊杆力(266 kN)相差最小，误差为0.1%。方案5：D10成桥吊杆力(231 kN)与设计成桥吊杆力(280 kN)相差最大，误差达17.4%，D6成桥吊杆力与设计成桥吊杆力相差最小，两者几乎一致(均为237 kN)。

综上所述，方案3的成桥吊杆力与设计成桥吊杆力最接近，误差均在0.2%以内。

4.2 拱肋混凝土应力对比

张拉吊杆时，拱肋局部位置截面上下缘会出现拉应力，由于拱肋混凝土中不含纵向钢筋，需要控制其拉应力在较小的范围内，因此有必要对吊杆张拉过程中拱肋混凝土中出现的拉应力进行对比。由于吊杆张拉过程中，拱肋混凝土的压应力不控制设计，因此只对拱肋混凝土拉应力进行对比分析。考虑到吊杆张拉顺序不同，出现拉应力的截面位置也会有不同，因此对吊杆张拉过程中、施工二期及运营30年等施工阶段整个拱肋混凝土中出现的最大拉应力进行对比分析。吊杆张拉过程中拱肋混凝土截面上缘和截面下缘的最大拉应力分别如表3、表4所示。

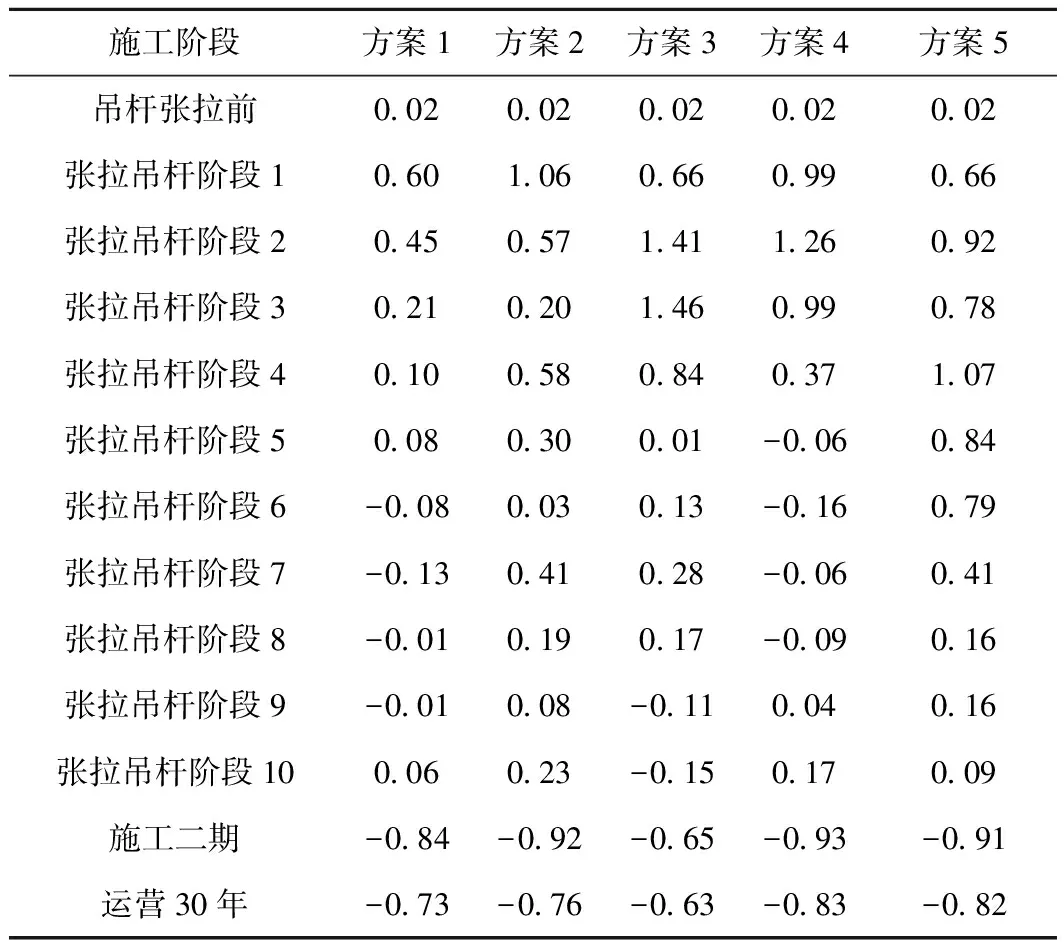
表3 施工过程中拱肋混凝土截面上缘最大拉应力 MPa

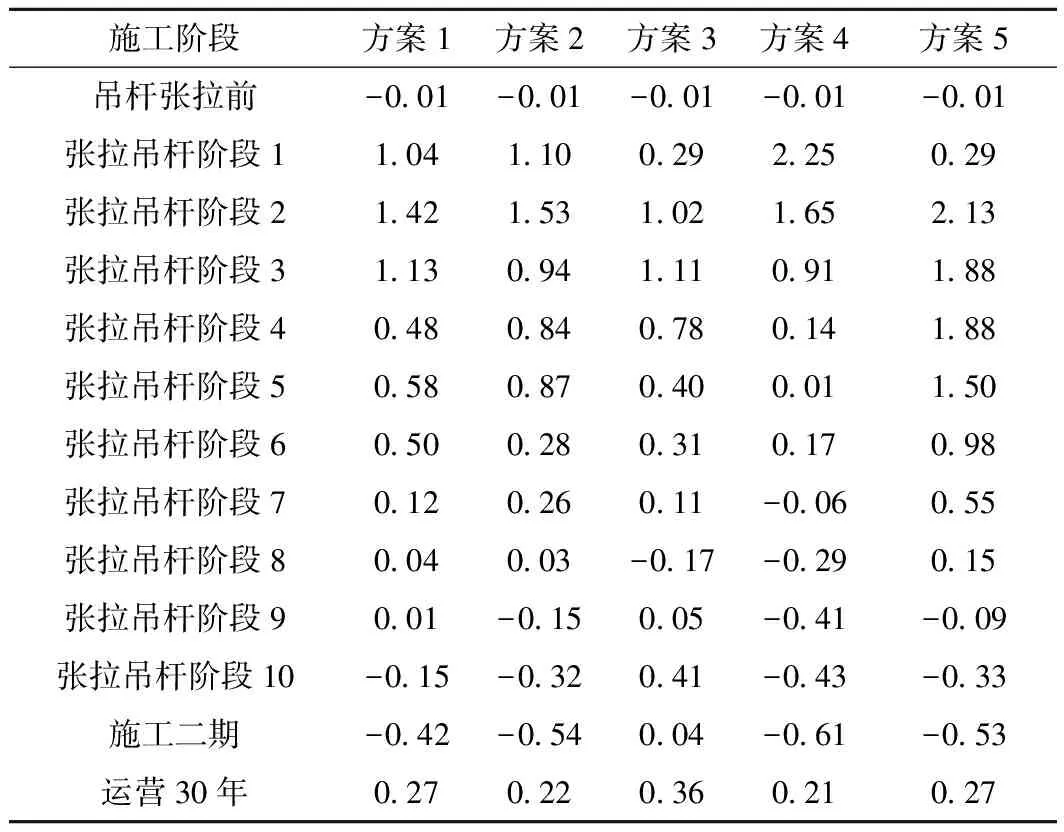
表4 施工过程中拱肋混凝土截面下缘最大拉应力

由表3可知，各张拉方案的拱肋混凝土截面上缘最大拉应力均在限值1.49 MPa以内，其中方案1的最大拉应力最小，为0.6 MPa，方案3的最大拉应力最大，为1.46 MPa。由表4可知，拱肋混凝土截面下缘的最大拉应力均比截面上缘的最大拉应力大，其中方案2，方案4，方案5的最大拉应力均超过限值1.49 MPa，方案4的最大拉应力更是达到了2.25 MPa，超出限值较多。方案3的最大拉应力最小，为1.11 MPa，方案1的最大拉应力其次，为1.42 MPa。

在施工二期和运营30年等施工阶段，5种方案的拱肋混凝土截面上缘均处于受压状态。截面下缘虽出现了拉应力，但数值较小，且各方案之间相差不到0.2 MPa，故不作为比较依据。

综合对比5种吊杆张拉方案拱肋混凝土截面上缘和截面下缘的最大拉应力，可以看出，方案1较优，方案3其次，其余方案在吊杆张拉过程中拱肋混凝土均出现了超过限值的拉应力。

4.3 拱肋钢管应力对比

与拱肋混凝土不同，拱肋钢管在施工过程中均处于受压状态，其压应力控制设计，因此有必要对吊杆张拉过程中、施工二期及运营30年等施工阶段整个拱肋钢管中出现的最大压应力进行对比分析。拱肋钢管截面上缘和截面下缘的最大压应力分别如表5、表6所示。

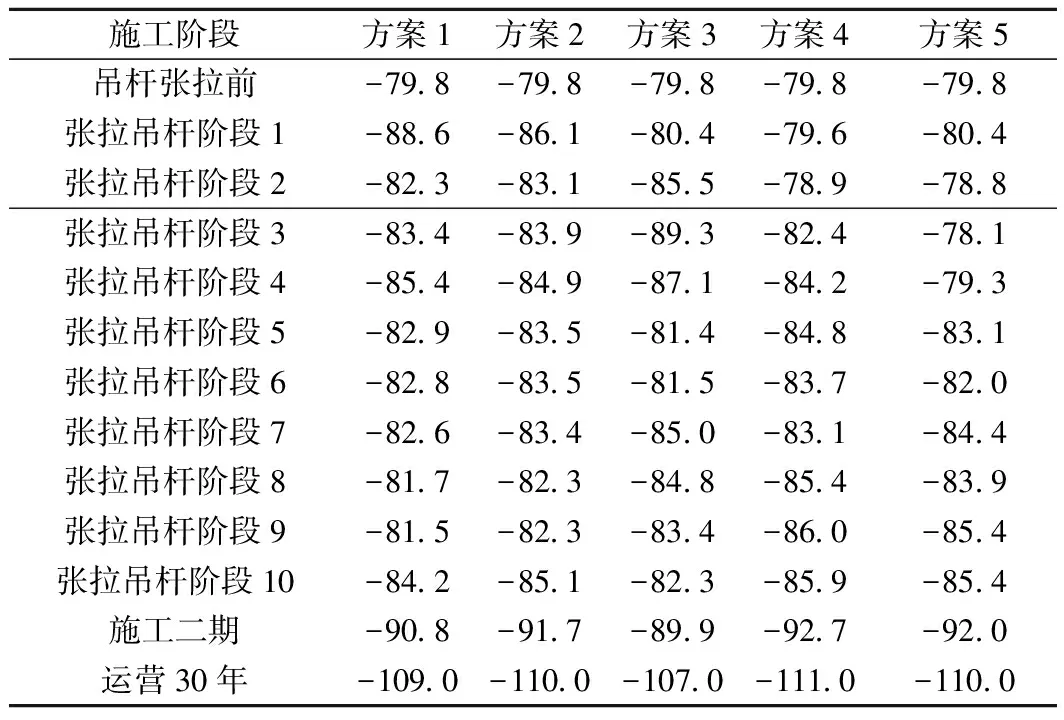
表5 施工过程中拱肋钢管截面上缘最大压应力 MPa

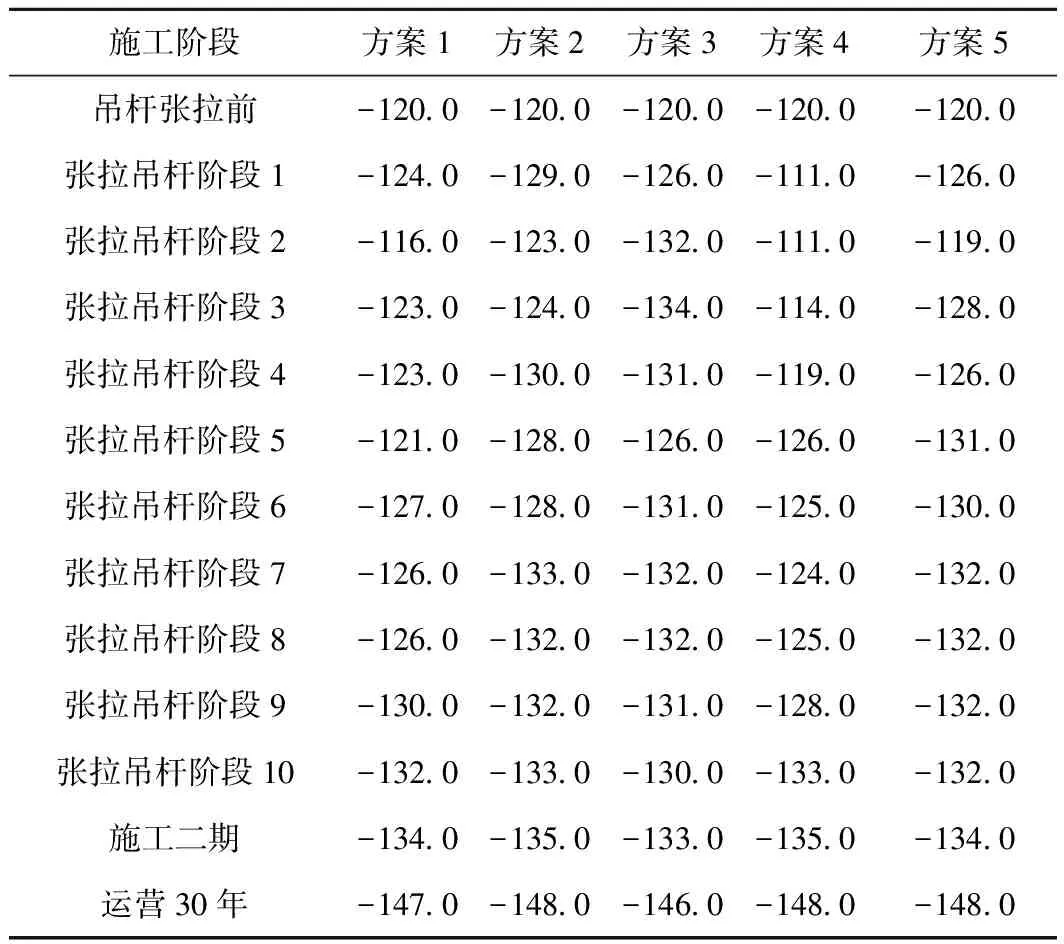
表6 施工过程中拱肋钢管截面下缘最大压应力 MPa

由表5、表6可知，在吊杆张拉阶段，各张拉方案的拱肋钢管截面上、下缘压应力最大值均远小于拱肋钢管应力限值252 MPa，且相差不大，故不作为比较依据。而在施工二期、运营30年等施工阶段，拱肋钢管压应力有所增加，且运营30年阶段的拱肋钢管应力占运营阶段拱肋钢管应力的绝大部分，因此以运营30年阶段的拱肋钢管应力为依据进行对比分析。

从表5、表6可以看出，运营30年阶段，方案3的拱肋钢管截面上、下缘压应力最小(上缘107 MPa，下缘146 MPa)，方案1的次之(上缘109 MPa，下缘147 MPa)，其余方案截面上、下缘压应力较方案3和方案1均有所增大。

4.4 拱肋位移对比

对各张拉方案在吊杆张拉过程中的拱顶和1/4拱肋处的竖向位移进行对比分析，结果如表7、表8所示。

表7 吊杆张拉过程中拱顶竖向位移 mm

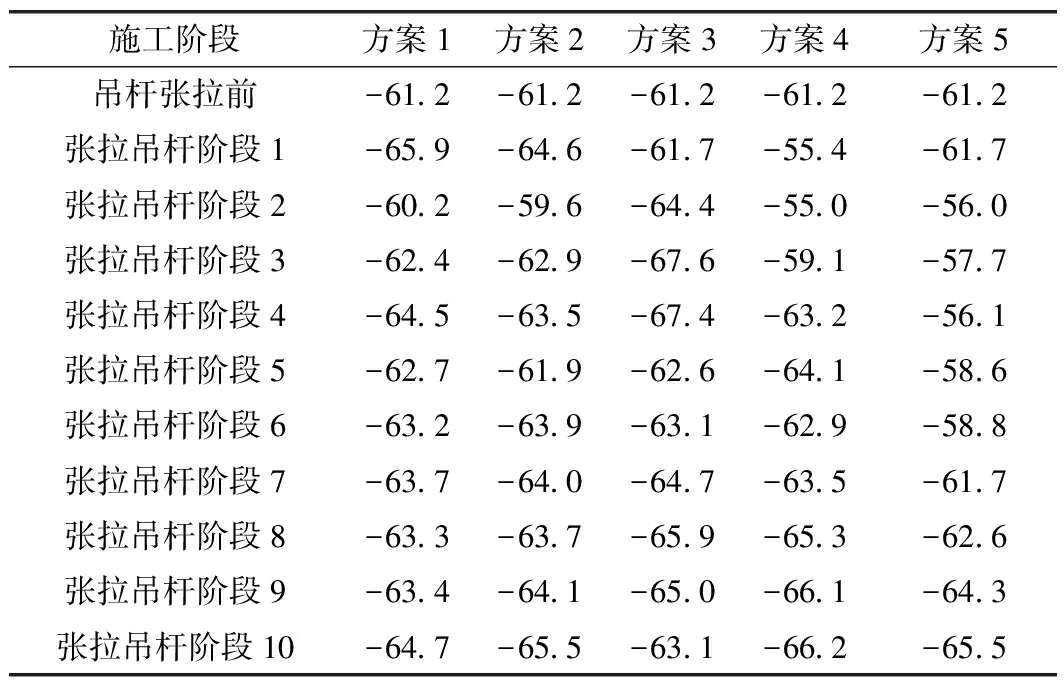
表8 吊杆张拉过程中1/4拱肋处位移 mm

由表7可知，方案1、方案2、方案4、方案5在张拉第2根吊杆后，拱顶竖向位移就迅速增大，且一直保持较大位移值，其中方案4的位移值最大。方案3的拱顶竖向位移变化较平顺，在张拉第5根吊杆后拱顶竖向位移才开始增大，且其最大位移值在各吊杆张拉方案中处于平均水平。由表8可知，方案1～方案3的1/4拱肋处竖向位移变化均较为平顺，而方案4和方案5的1/4拱肋处竖向位移变化较大。

通过对比拱顶和1/4拱肋处的竖向位移可看出，方案3较优。

4.5 拱脚水平推力

对各张拉方案在吊杆张拉过程中的拱脚水平推力进行对比，结果如表9所示。

表9 吊杆张拉过程中拱脚水平推力 kN

从表9可以看出，吊杆张拉过程中各吊杆张拉方案的拱脚水平推力值相差不大，且拱脚水平推力变化均较为平顺，说明吊杆张拉方案的不同对拱脚水平推力的影响较小。

4.6 主梁应力

为对比吊杆张拉方案对主梁截面应力的影响，选取吊杆张拉过程中中跨跨中位置截面上、下缘的应力进行对比，结果如表10所示。

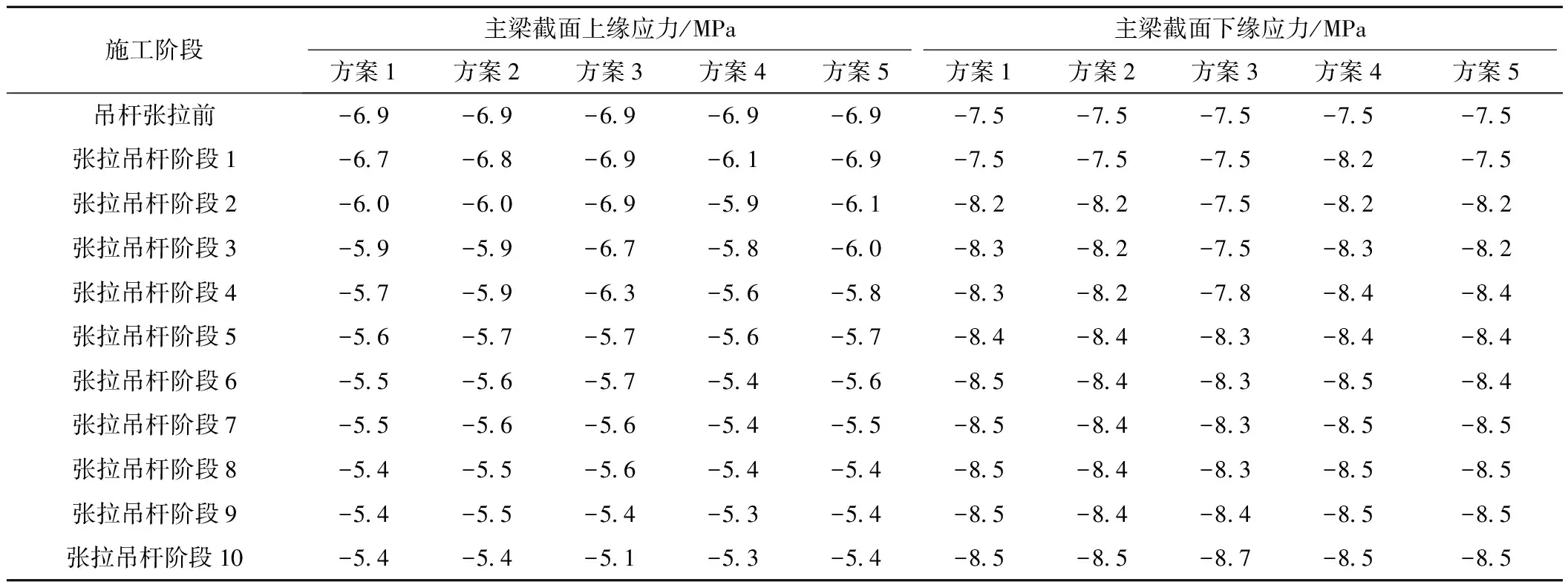
表10 吊杆张拉过程中中跨跨中处截面应力

由表10可知，吊杆张拉过程中各吊杆张拉方案的主梁截面上、下缘应力值相差不大，不超过0.2 MPa，且各方案的主梁应力呈现出较好的线性变化。说明吊杆张拉方案的不同对主梁应力的影响较小。

5 结论

现有的关于吊杆张拉方案的研究多数集中于简支梁拱组合体系桥梁，为研究连续刚构拱体系桥梁的合理吊杆张拉方案，对昌景黄铁路义城昌江特大桥(90+200+90)m连续刚构拱的吊杆张拉方案进行了研究，提出了5种吊杆张拉方案，分别是：(1)四分区-拱顶-拱脚交替张拉；(2)拱脚-拱顶-四分区交替张拉；(3)从拱脚至拱顶交替张拉；(4)从拱顶至拱脚交替张拉；(5)先拱脚-拱顶交替张拉再四分区张拉。通过有限元软件进行吊杆张拉过程的模拟，对5种吊杆张拉方案下的成桥吊杆力，拱肋混凝土应力，拱肋钢管应力，拱肋位移，拱脚水平推力，主梁应力进行对比分析，得出以下结论。

(1)方案3的成桥吊杆力与设计成桥吊杆力最接近，误差均在0.2%以内。

(2)吊杆张拉过程中方案1的拱肋混凝土截面上、下缘最大拉应力控制得最为合理，方案3其次，其余方案在吊杆张拉过程中拱肋混凝土均出现了超过限值的拉应力。

(3)运营30年阶段方案3的拱肋钢管截面上、下缘压应力最小，方案1次之，其余方案截面上、下缘压应力较方案3和方案1均有所增大。

(4)吊杆张拉过程中方案3的拱顶和1/4拱肋处竖向位移变化较为平顺，且其最大位移值在各吊杆张拉方案中处于平均水平。

(5)吊杆张拉方案对拱脚水平推力和主梁应力的影响均较小，各吊杆张拉方案的拱脚水平推力和主梁应力均呈现较好的线性变化。

综合以上几项对比分析结果，对于(90+200+90)m钢管混凝土连续刚构拱桥，方案3为相对最优的吊杆张拉方案。