矩阵能量与其迹的关系研究

金旭梅,李崇民,李 静

(青海师范大学 数学与统计学院,青海 西宁 810016)

利用矩阵的迹的不等式[1-4]，文献[5]给出Kronecker积上的一个矩阵不等式和文献[6]解决了Ando关于特征值的Bloomfield-Watson型不等式的三个问题，并推广了Kantorovich不等式.文献[7]通过多级蒙特卡罗方法随机估计多重网格的迹.

迹作为矩阵的一个重要的相似不变量，与矩阵的特征根相关的不变量存在密切联系.当矩阵A是图G的邻接矩阵，则所有特征根的绝对值之和是图G的图能量[8].当矩阵A是有向图D的邻接矩阵，则所有特征根的实部之和是图D的有向图能量[9].因为图的邻接矩阵的特征根都是实数，所以图能量是有向图能量的特殊情形.事实上，有向图能量可以推广到更一般的情形，定义如下矩阵能量：

图能量在化学、统计物理和生物学领域存在广泛的应用，相关的结果比较丰富[10-13].国外学者Rada利用矩阵的迹研究了关于有向图邻接矩阵的迹与特征根的关系[14]，获得了关于有向图能量紧的下界,并刻画了具有最小有向图能量的有向图.更多的关于有向图能量的研究，我们可以在文献[15-17]中找到.

进一步的，为探索矩阵的迹与特征根的更一般的性质，本文通过二次型展开式和实部与虚部的比较等方式，探讨了矩阵特征根与迹的关系,获得若干用矩阵的迹来表示的矩阵能量的下界.基于矩阵能量与其迹的关系，本文展示了矩阵能量在简单图和有向图中的应用.

1 基于实特征根的矩阵能量

定理1.1[14]设A是n×n的复矩阵，特征值为z1,z2,……,zn，则

等式成立当且仅当A是幂零矩阵或者所有z1,z2,……,zn都是实数，仅只有两个特征值是非零且它们的符号相反.

推论1.2 设A是n×n的实矩阵,如果对应的特征值为实数λ1,λ2,……,λn，则

推论1.2得到了E(A)2关于矩阵的迹不等式，下面我们考虑E(A)3.

定理1.3 设A是n×n的实矩阵，如果对应的特征值为实数λ1,λ2,……,λn，则

观察上述结果，E(A)2和E(A)3都能与矩阵的迹存在关系.接下来继续讨论E(A)4的情形.

定理1.4 设A是n×n的实矩阵，如果对应的特征值为实数λ1,λ2,……,λn，则

证明由推论1.2可得，则

因为

所以tr(A2)tr(A2)≥tr(A4).因此

更一般地考虑分别按矩阵能量的偶数次方和奇数次方来讨论矩阵能量与迹之间的关系.

定理1.5 设A是n×n的实矩阵，如果对应的特征值为实数λ1,λ2,……,λn，则

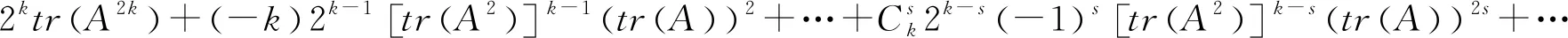
其中：k=1,2,…,n和1≤s≤k.

因为

定理1.6 设A是n×n的实矩阵，如果对应的特征值为实数λ1,λ2,……,λn，则

其中:k=1,2,…,n和1≤s≤k.

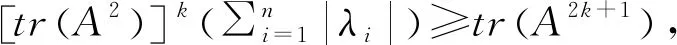
当取矩阵能量的奇数次方时，如果我们把矩阵A看作图的邻接矩阵，那么tr(A)=0定理1.6中的不等式就可以简化成E(A)2k+1≥2ktr(A2k+1).

2 基于复特征根的矩阵能量

前面讨论了基于实特征根的矩阵能量与迹的关系，接下来讨论基于复特征根的矩阵能量与迹的关系.

定理2.1 设A是n×n的复矩阵，特征值为z1,z2,……,zn, 则

其中：zj=aj+ibj，1≤j≤n.

证明已知

因此

当特征根有复数时，通过比较实部大小以及利用实部与虚部的乘积，得到矩阵能量与迹的关系.

定理2.2 设A是n×n的复矩阵，特征值为z1,z2,……,zn，其中zj=aj+ibj，1≤j≤n.此外，满足

证明由定理1.1可得，有

又因为

……

因此

即有

3 矩阵能量的图应用

基于第一节和第二节的结论，本节将前两节结论应用到简单图和有向图的情形.

当矩阵A是简单图G的邻接矩阵时，显然有tr(A)=0，应用定理1.5可得E(A)2k≥2ktr(A2k).

例3.1如图1所示，图G1为顶点数为6的图.通过直接计算可得，Spec(G1)={3,1,-2,-2,0,0},E(A)=8.

同理，当矩阵A是简单图G的邻接矩阵时，由定理1.6可得E(A)2k+1≥2ktr(A2k+1).

例3.2如图2所示，图G2为顶点数为8的图，通过计算可得

当矩阵A是有向图D的邻接矩阵时，则Retr(A)=0.应用定理2.1可得

例3.3如图3所示，图D1为顶点数为7的有向图，

图1 简单图G1 图2 简单图G2 图3 有向图D1

备注：本工作由如下单位及项目资助.青海省部共建藏语智能信息处理及应用国家重点实验室；藏文信息处理教育部重点实验室；青海人民政府—北京师范大学高原科学与可持续发展研究院；111引智计划(D20035).