一类含有cos函数项的新超混沌系统的动力学分析及自适应控制研究

陈 恒,代文鹏 ,李勇兴 ,颜廷洋

(1.西京学院 机械工程学院，陕西 西安 710123；2.山东海事职业学院 中职学院；山东 潍坊 261108；3.齐鲁理工学院 智能制造与控制工程学院，山东 济南 250200)

混沌是在一定参数范围内出现的一种类似随机过程的非线性行为[1-3]，随着混沌研究及发展，新的整数阶及分数阶混沌系统不断提出[4]，纠缠系统[5]、多翼系统也广泛应用到实践中[6].如图像混沌加密[7-10]、电机和电源控制系统及控制工程领域如何有效的同步控制应用[11-12].

然而实际项目应用模型比理想模型复杂，那么能否在Lorenz系统的基础上构造含有平方项与cos函数项的新复杂混沌系统，研究其动力学行为并进行同步控制，对实际工程提供了新的思想.针对该系统的相图、分岔图、LE指数分析了系统数值参数的敏感性行为，进行了混沌电路及自适应同步控制器设计仿真.

1 混沌系统与分析

在Lorenz系统上构造的一类含有cos函数项及平方项组成的四维非线性超混沌系统.

(1)

x,y,z,w作为系统变量，系统参数a，b，c，d，k，当a=10,b=10,c=1,d=8/3,k=5，根据方程(1)做出变量吸引子如图1.经推算得到系统LE指数为λ1=1.1,λ2=1.1,λ3=0,λ4=-13.7，因为λ1>0，λ2>0，所以构造的系统具有超混沌特性[13].

1.1 耗散性

由于

(2)

图1 相图

1.2 平衡点及稳定性

a=10,b=10,c=1,d=8/3,k=5,在系统(1)的基础上令等各式为零，得系统平衡点E0：E0=(1.235,0.905,0.572,-24.897).最后对E0=(1.235,0.905,0.572,-24.897)的Jacobian矩阵进行特征值计算：

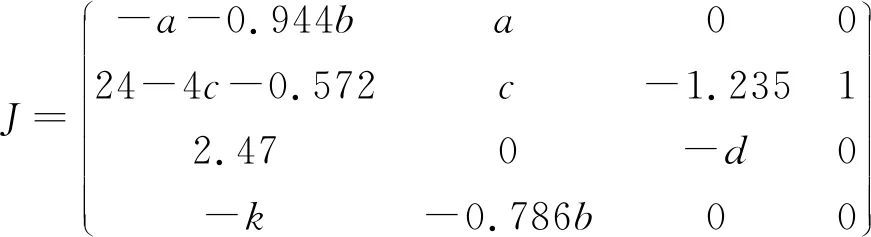
(3)

特征方程为

f(λ)=λ4+21.1λ3-156.7λ2-315.7λ-540.8.

(4)

特征值为λ1=-26.5344，λ2=6.8432，λ3=1.1575，λ4=-2.573，根据劳斯-赫尔维茨稳定判据，E0为不稳定的平衡点[15].

2 参数的影响

a=10,b=10,d=8/3,k=5，c∈[0,8]，从系统(1)的LE指数与x分岔图(图2)得出超混沌区存在于c∈[0,4]阶段，c∈[4,5.5]呈现出混沌态，c=5.5后以周期现象结束.如图3，c=1.5、c=4.5、及c=8分别为超混沌、混沌及周期位置点.根据图2(c)发现，LE1整体下降趋势，也说明了c对系统的混沌影响逐步减小.

图2 系统(1)c变化分岔图与LE指数图

图3 c变化时相图

a=10,c=1,d=8/3，k∈[0,40]，系统(1)k变化的LE指数及x分岔图(图4)看出k∈[1,10]∪[19,22]表现出超混沌特性，k=35后，产生周期区间并持续到结束，其余区间为混沌特性.从图4(c)LE1中发现系统整体混沌复杂特性呈现下滑趋势，说明k值越大，对系统混沌影响越小.为验证这3个特殊位置，图5做了从超混沌到混沌再到周期的相图.

图4 系统(1) k变化分岔图与LE指数图

图5 k变化相图

当a=10，b=10，c=1，k=5，d∈[0,6]，从系统(1)LE指数及x分岔图(图6)看出d∈[0,5]呈现为混沌态，d=5后续过程走向拟混沌态.从图6(c)的LE1走向发现，d=4附近对系统混沌影响最大.

a=10，c=1，d=8/3，k=5，b∈[0,10]，系统(1)LE指数及x分岔图(图7)得到b∈[0,10]阶段表现形式为超混沌特性.根据图7(c)发现LE1整体上为减小趋势，说明系统复杂度随着b增大而降低，b越小，混沌性越强.

图6 系统(1)d变化分岔图与LE指数图

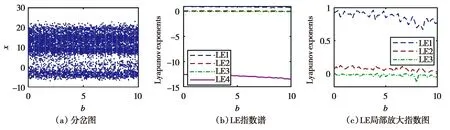
图7 系统(1)b变化分岔图与LE指数图

b=10，c=1，d=8/3，k=5，a∈[2,10]，从系统(1)LE指数及x的分岔图(图8)得到a∈[2,4]的周期态，a=4之后的混沌阶段.根据图8(c)发现LE1整体上为上升趋势，说明系统复杂度随着a增大而增加，a越大，混沌性越强.

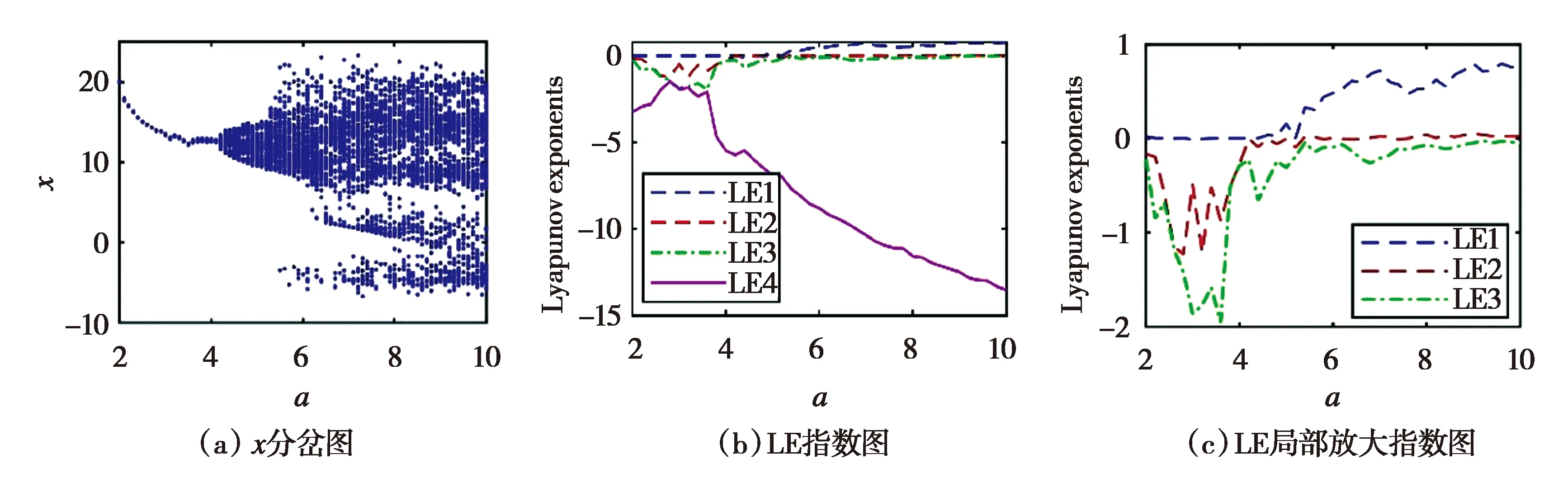
图8 系统(1)a变化分岔图与LE指数图

3 混沌电路设计

根据系统(1)方程，利用Multisim14调制出由受控电源、运算放大器LM741、乘法器、电容电阻等组成的仿真电路，如图9.

图9 系统(1)电路图

根据图9，写出电路方程(5)，其方程与系统(1)对应.

(5)

Multisim14对混沌电路进行搭建及调理仿真，用示波器实时观察x,y,z，w电压值状态，验证相图(图10)，输出效果与理论计算一致.

图10 系统(1)电路仿真相图

4 自适应同步控制器的研究

为进一步利用该系统，设计自适应同步控制器.驱动系统为：

(6)

响应系统为

(7)

式(7)中u控制输入，d未知.

误差为

(8)

误差系统为

(9)

Lypunov为

(10)

V的导函数为

(11)

取控制率为

(12)

自适应率为

(13)

则：

(14)

5 仿真结果

a=10,b=10,c=1,k=5，d=2.驱动与响应系统初值x10=-3,y10=12,z10=18,w10=1,x20=9,y20=-20,z20=10,w20=6,Matlab仿真得到同步控制器的同步及误差结果如图11、12.t=5s后，驱动及响应系统在时空上接近同步，该同步控制器设计方法有效.

图11 驱动及响应系统同步图

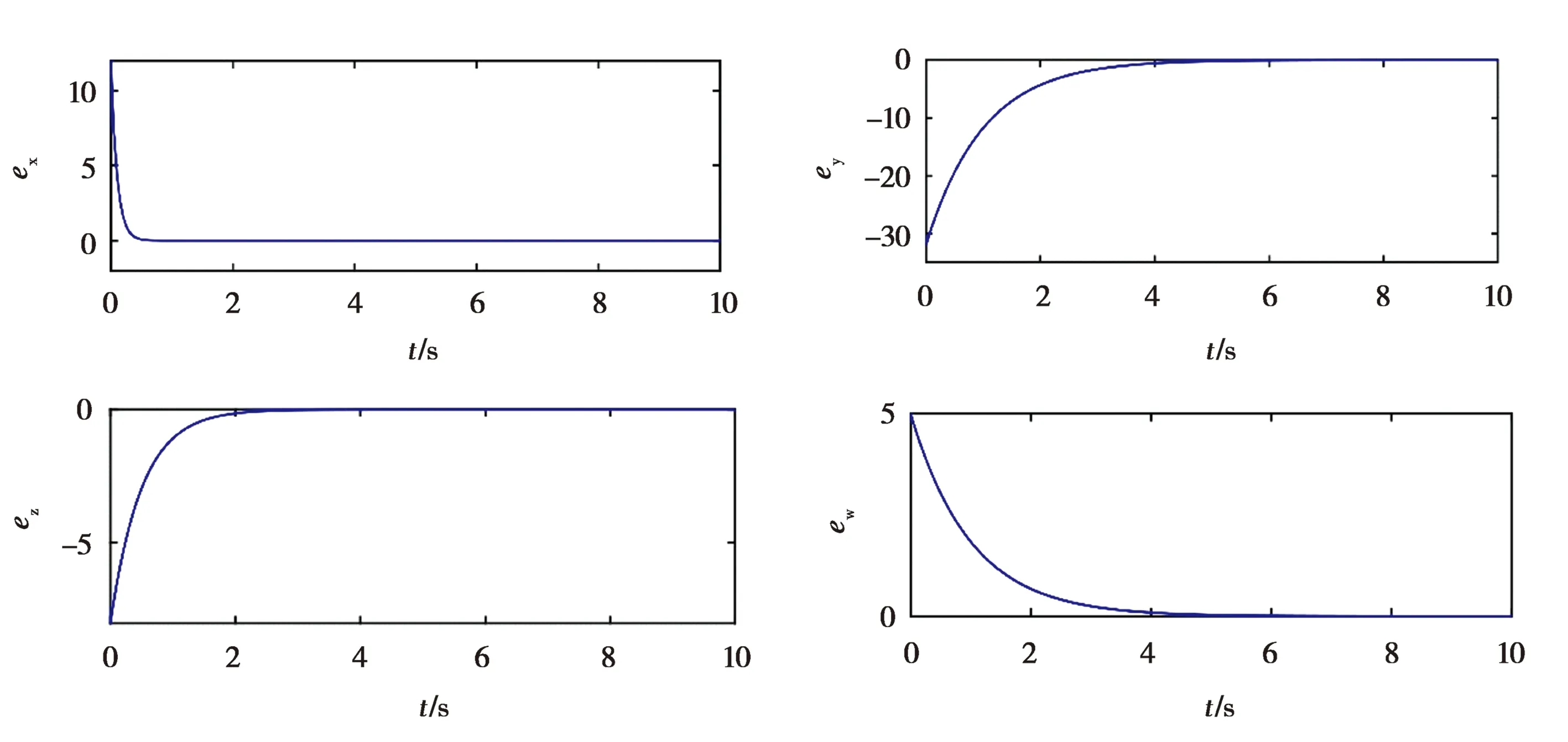
图12 驱动及响应系统误差图

6 结论

通过对该系统的数值计算、电路信号的调理计算仿真及参数对系统变化的动力学影响说明了该系统具有参数敏感性的动力学行为、混沌调理电路的可操作性，最后，通过自适应同步方法的计算，证明了两系统在有限时间内达到同步目的，研究结果不仅对混沌同步控制研究提供了思路，也对混沌保密通讯、图像加密及电源混沌控制等方面提供了一定的研究价值.