水资源利用与排污控制的非合作博弈方法
付 湘,谈广鸣,黄 莎,刘双郡
(1.武汉大学 水资源与水电工程科学国家重点实验室,湖北 武汉 430072;2.武汉大学 海绵城市建设水系统科学湖北省重点实验室,湖北 武汉 430074)
1 研究背景
社会经济用水后的污染排放量对水生态环境施加压力负荷,带来水资源短缺、水环境污染、水生态破坏等诸多问题,而水生态环境的破坏反过来制约着水资源利用[1]。《中共中央关于制定国民经济和社会发展第十四个五年规划和二〇三五年远景目标的建议》指出:绿水青山就是金山银山,坚持尊重自然、保护优先,主要污染物排放总量持续减少,完善环境保护约束性指标管理。”这明确了生态环境具有重要的经济价值,良好的生态环境是经济可持续发展的基础,过度开发利用水资源、破坏水生态环境必然会影响社会经济发展质量。
水资源开发利用与水环境保护等多目标之间相互矛盾、相互竞争的情况下,利益相关主体进行的决策,常使用多目标决策方法[2-4],该方法以系统科学为理论基础,运用最优化理论求解水资源安全的社会、经济与环境目标,这是一种自上而下的理想方法。该方法假定存在权威的决策者,不存在满足各个目标的同时最优解,而是非劣解集,不是唯一的解而是一组解。在非劣解处,改善一个目标函数的效益,必以牺牲其他目标函数的利益为代价,在解决实际问题中,被选中的解只是非劣解集中权威决策者的偏好解[5-6]。由于多目标优化决策方法强调最优化整体利益而忽视个体利益,引发个体利益与整体利益冲突[7],出现整体效率与个体公平困境,使水资源利用安全面临挑战。
博弈论方法突破了传统多目标优化决策的效率和公平困境,能更好地模拟多个主体相互作用的利益冲突问题[8]。博弈根据是否可以达成具有约束力的协议分为合作博弈和非合作博弈,合作博弈着重研究集体行为特点,关心合作得到的收益并能够分配各方的收益[9];非合作博弈侧重个体行为特征研究,各博弈方通过理性竞争方式实现各自目标效益最大化[10]。在有约束力的合作协议难以达成的情况下,非合作博弈方法将成为博弈研究的重要方向[11-12]。
非合作博弈中的讨价还价方法是指博弈参与者通过协商方式解决利益分配的问题,讨价还价的纳什均衡解为博弈参与者在给定约束条件下,最大化自身的效用函数的均衡解。如:Lee[13]针对台湾省曾文水库的库区土地利用优化问题,建立了多目标非合作博弈模型,该模型描述了库区土地利用的污染负荷-总磷最小目标与土地利用经济效益最大目标函数,详细介绍了两个目标之间的讨价还价直至达成纳什均衡的过程。Nasiri-Gheidari 等[14]构建了农作物生产中的排水污染负荷-总溶解固体最小与农作物收入最大为目标的优化模型,将讨价还价方法应用于伊朗的跨流域水资源配置问题。
非合作博弈中的主从博弈方法是一种由于双方地位不平等而出现先后决策的动态博弈行为,博弈双方一个处于领导者地位,而另一个处于跟从者地位,领导者在制定策略时需要充分考虑跟从者的响应模型。Chen 等[15]将总污染物排放量最小视为上层领导者的目标,将总用水净效益最大视为下层跟从者的目标,建立水资源管理的主从博弈模型,并以北京市丰台区为例开展模型的应用研究。Sedghamiz 等[16]建立了以水资源管理者为领导者、农业用水部门为跟从者的主从博弈模型。Mooselu 等[17]将污水输送费用和总缺水率最小视为上层领导者的目标、各地区缺水率最小视为下层跟从者的目标,建立了主从博弈优化模型,解决伊朗德黑兰地区的污水分配问题。
尽管非合作博弈方法在水资源配置中的研究文献比较丰富,但这些文献大多侧重于通过非合作博弈模型达到纳什均衡。对于追求自身利益的平等关系与不平等关系博弈主体获得纳什均衡解的协商过程与交互过程,以及非合作博弈的均衡解与多目标优化的非劣解之间的关系与内涵,还需要从理论方法研究深入到具体问题分析。本文针对决策冲突主体之间难以达成有约束力的合作协议情况,提出水资源利用与排污控制的讨价还价博弈方法与主从博弈方法,并对比分析纳什均衡解与非劣解之间的关系,解决先行用水给后续排污带来的负外部性问题,实现水环境保护优先的前提下发展水经济。
2 非合作博弈方法
非合作博弈方法强调决策主体的个体理性,个体决策最优。为实现水环境保护优先的前提下保障水资源持续利用,本文研究的非合作博弈方法假定水环境保护主体为生态环境保护部门,水资源经济利用主体为用水部门。根据决策主体之间的平等协商关系与不同地位的递阶结构,研究水资源利用与排污控制的讨价还价博弈方法与主从博弈方法。
2.1 水资源利用与排污控制的讨价还价博弈方法讨价还价博弈方法着重于强调博弈主体的决策行为和协调过程,针对水资源利用与排污控制的冲突问题,本节运用讨价还价博弈方法,假定水环境保护主体(生态环境保护部门)和水资源经济利用主体(用水部门)是具有平等地位的博弈决策主体,构建讨价还价博弈模型并进行求解。
水环境保护主体的目标描述为排污总量最小,目标函数式为:
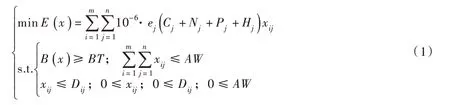
水资源经济利用主体的目标描述为经济效益最大,目标函数式为:

式(1)与(2)表示水环境保护主体与水资源经济利用主体的讨价还价博弈过程,水资源经济利用主体的目标值约束B(x)≥BT写在式(1)约束条件下,是为了体现水环境保护主体的优化模型中与水资源经济利用主体的协商过程;同理,水环境保护主体的目标值约束E(x)≤ET写在式(2)约束条件下,是为了体现水资源经济利用主体的优化模型中与水环境保护主体的协商过程;有别于传统的单目标优化模型。
在博弈主体的讨价还价过程中,当水环境保护主体达到最优策略时,水资源经济利用主体的效益值低于其最优目标值,同样地,当水资源经济利用主体达到最优策略时,水环境保护的排污总量高于其最优目标值,某一博弈主体的最优策略并不能满足对方的最优策略,需要重复地进行谈判直到没有任何一方愿意偏离这种策略为止,其表达式如下:

式中E *(x)与B *(x)分别为水环境保护主体与水资源利用主体的最优策略。
同时满足式(3)与(4)的解即为讨价还价博弈的纳什均衡解。根据上述讨价还价博弈的纳什均衡解概念,本文运用一致后退讨价还价法对模型进行求解[18]。一致后退讨价还价法是后退式讨价还价法的重要分支,各博弈主体根据个体理性要求将所有可行性策略进行降序排列,在第一轮讨价还价中每个博弈主体均提出自身的最优策略,如果每个博弈方提出的最优策略一致,则没有任何一方主动提出背离该策略,进而讨价还价过程结束,获得各博弈主体的最优策略。如果每个博弈方提出的最优策略不一致,并且若执行一方的最优策略将大幅度牺牲另一方的利益,在实际中无法实现该策略,则进入第二轮讨价还价。在第二轮讨价还价中每个博弈方根据第一轮讨价还价的目标策略进行调整提出次优策略,对于前两轮讨价还价提出的所有策略,如果有至少一个策略被所有博弈主体所接受,则讨价还价结束。如果前两回合没有达到一致,则进入下一轮讨价还价,直至最优策略集合首次非空:

式中:d*为讨价还价停止的回合数;k为非劣策略总数;n为博弈方的总数;|CS|为最优策略集合中的策略数目。
2.2 水资源利用与排污控制的主从博弈方法主从博弈方法是一个上下级层次结构的系统优化问题[8],上层领导者先行动,下层跟从者随后行动,跟从者的决策依赖于领导者的决策,领导者也会基于跟从者的反馈进行策略调整,体现出水资源利用冲突中主体的复杂关系与行为次序,更好地展现了各方策略协调过程的交互特性。
水资源利用与排污控制的主从博弈方法假定水环境保护主体为上层领导者,水资源经济利用主体为下层跟从者,他们是具有主从关系的博弈决策主体。上层领导者的目标为排污总量最小,下层跟从者的目标为经济效益最大,主从博弈模型的表达式如下:
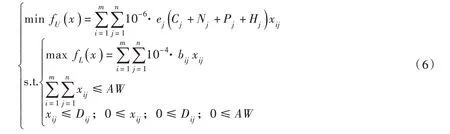
式中:fU(x)为上层水环境保护主体的排污总量,万t;fL(x)为下层水资源经济利用主体的经济效益,亿元。
主从博弈模型(6)采用双层模糊优化方法求解[19-20]。考虑在上、下层决策相互影响的主从博弈模型中,上层领导者直接用上层最优解对下层跟从者进行控制并不符合实际,因此,将上层领导者与下层跟从者的目标函数描述为隶属度函数,以反映上层目标与下层目标的满意度;并引入上层决策变量范围的隶属度函数,允许下层跟从者在该容许范围内寻找最优解,相对减少了寻优时间。
主从博弈模型的目标函数转化为上、下层隶属度函数的公式如下:
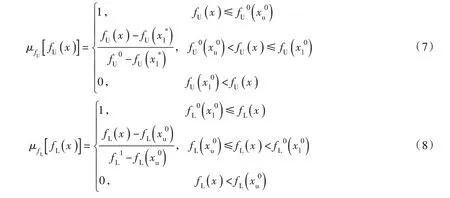
对于上层隶属度函数式(7),上层领导者希望排污总量目标越小越好,当时,表示上层目标函数值小于等于其单独优化值,上层目标函数隶属度为1,表示达到了上层领导者的目标;当时,表示当上层目标函数值大于下层最优解代入上层目标函数所得到的值,上层目标函数隶属度为0,表示上层领导者拒绝下层反馈的解。说明在主从博弈中,上层领导者希望最优决策变量使得上层目标函数越接近其单独求解的最优值越好。
对于下层隶属度函数式(8),下层跟从者希望经济效益目标越大越好,当时,表示下层目标函数值大于等于其单独优化值,下层目标函数隶属度为1,表示达到了下层领导者的目标;当时,表示当下层目标函数值小于上层最优解代入下层目标函数所得到的值,下层目标函数隶属度为0,表示下层跟从者不接受上层提供的解。说明在主从博弈中,下层跟从者希望最优决策变量使得下层目标函数越接近其单独求解的最优值越好。
在上层领导者与下层跟从者的交互过程中,上层领导者给下层跟从者一个可接受的决策变量范围,上层决策变量的隶属度函数的公式如下:

式中:xu为上层决策变量;d为上层最优决策解周边的最大容忍范围,说明在在主从博弈中,上层领导者希望其最优决策变量越接近上层目标函数单独求解的最优值越好。
综合隶属度函数(7)、(8)与(9),主从博弈模型(6)的求解公式转换为:

式中:θ、θU分别为主从博弈模型的整体满意度、上层领导者的满意度;θU1为上层领导者可接受的决策变量最小隶属度;θU2为上层领导者可接受的目标函数最小隶属度;θL为下层跟从者的满意度; I 为元素为1 的列向量。
双层模糊规划问题(10)中,上层领导者与下层跟从者的满意度用隶属度表示,若达到上层和下层决策问题的满意程度,则得到最终结果;否则,上层决策问题会向下层决策问题提供新的隶属度函数作为控制变量和目标,直至得到主从博弈模型最优解。
3 实例研究
本文的研究区域为洞庭湖四口河系的7 个水资源分区,分别为华容河区(Ⅰ)、藕池东区(Ⅱ)、藕池中区(Ⅲ)、荆江区(Ⅳ)、松滋中区(Ⅴ)、松滋西区(Ⅵ)和松滋区(Ⅶ),如图1所示。洞庭湖四口河系随着社会经济快速发展,用水及其污染物排放量迅速增加,导致水资源紧缺与水质污染的双重危机。

图1 洞庭湖四口河系的7 个水资源分区
水资源利用与排污控制的讨价还价博弈模型求解需要的各用水部门排污系数,COD、TN、TP 和NH3-N的浓度,各水资源分区各用水部门需水量,用水效益系数,可供水量等数据,根据《湖南省第一次全国污染源普查公报》《湖南年鉴》《湖南水资源公报》等收集整理得到。本文实例研究为简化计算,假定用水效益系数、排污系数、污染物排放浓度在计算期内保持不变,该实例研究是针对区域案例开展的,如果应用到其他区域,相应的模型参数需要根据具体情况做出调整。
水资源利用与排污控制的讨价还价博弈模型求解过程见表1,在第一轮讨价还价中水资源经济利用主体目标值为580 亿元,水环境保护主体目标值为0.4 万t,运用式(1)求解出来的排污总量为10.63万t,不能满足水环境保护主体的目标值,运用式(2)求解出来的经济效益为216.99 亿元,不能满足水资源经济利用主体的目标值。从而进入第二轮讨价还价,经济效益主体逐渐降低其目标值为560 亿元,水环境保护主体目标值也降低其目标值,由于水环境保护主体希望目标值越小越好,排污总量目标值为0.8 万t,第二轮中运用式(1)求解的排污总量为9.24 万t,不能满足水环境保护主体调整的次优目标值,运用式(2)求解的经济效益为317.75 亿元,不能满足水资源经济利用主体的目标值。从而进入第三轮讨价还价,依次类推,直至第五轮讨价还价,运用式(1)—(5)求解,经济效益主体的目标值为460 亿元,此时排污总量最小为3.41 万t,排污总量主体的目标值为3.5 万t,此时经济效益最大为461.69 亿元,均满足两个主体的目标值,得到纳什均衡解为(460 亿元, 3.41 万t)~(461.69 亿元,3.5 万t)。通过模拟博弈主体间的讨价还价过程,体现了策略选择的动态交互过程。
水资源利用与排污控制的主从博弈模型运用式(7)—(10)求解,上层目标满意度θU与下层目标满意度θL的变化过程见图2。在主从博弈过程中,上层领导者的满意度为0.95 时,上层目标排污总量为0.67 万t;下层跟从者根据此决策,得出最优解为285.37 亿元,对应的目标满意度仅为0.47。上层领导者根据下层跟从者的反馈调整自己的决策,将置信水平从0.95 逐渐减少,按等距离Δ= 0.05 选取上层领导者的满意度θU=0.9,0.85,0.8,0.75,对应得到下层目标满意度为θL=0.6、0.659、0.713、0.752;当θU=0.75 时,整体满意度θ最大,上、下层目标满意度相等,各自的策略不再改变,此时各博弈主体均不能通过单独改变策略而获取更大的利益,其解为(457 亿元,3.24 万t),即主从博弈的纳什均衡解。
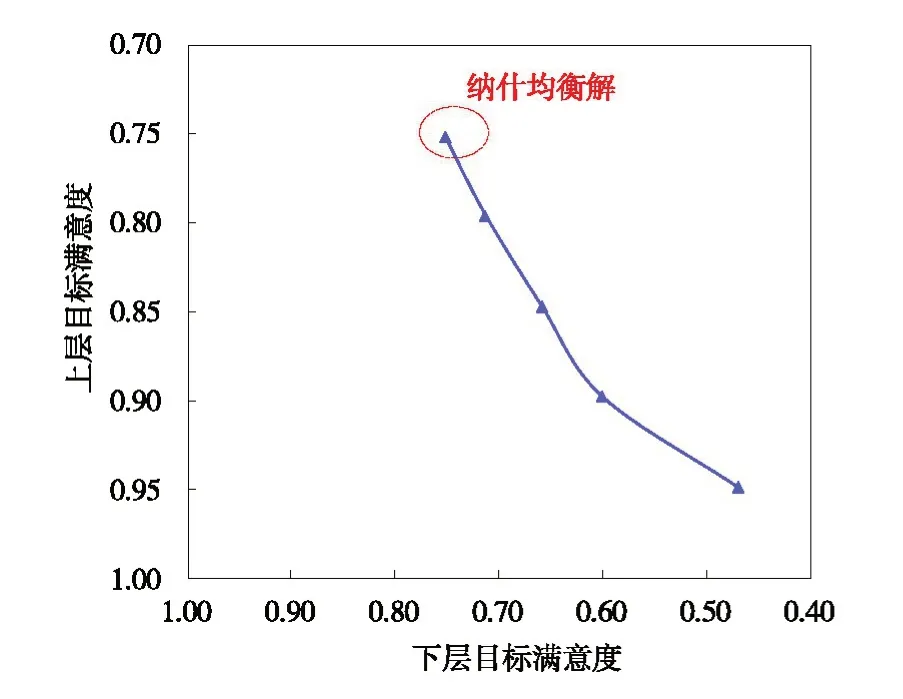
图2 水资源利用与排污控制的主从博弈过程
为比较非合作博弈方法与传统多目标优化方法在水资源利用与排污控制的结果差别,本文构建了以排污量最小和经济效益最大为目标函数的多目标优化模型并进行求解,得到多目标模型的Pareto解。讨价还价博弈模型、主从博弈模型与多目标优化模型的结果比较见图3,主从博弈模型和讨价还价博弈的纳什均衡解均在多目标模型的Pareto 前沿上。相比于多目标模型,讨价还价博弈通过模拟博弈主体考虑个体理性的策略选择过程,得到的纳什均衡解极大地缩减了多目标模型的策略空间。讨价还价博弈的纳什均衡解为(460 亿元,3.41 万t)~(461.69 亿元,3.5 万t),主从博弈的纳什均衡解为(457 亿元,3.24 万t),主从博弈模型的纳什均衡解与讨价还价博弈模型的纳什均衡解很接近,相比于讨价还价博弈模型,主从博弈模型通过上层和下层之间的决策互动过程,得到唯一的纳什均衡解,也是最优解。并且,主从博弈的纳什均衡解在讨价还价博弈的纳什均衡解右下方,表明了主从博弈的排污总量主体作为上层领导者更有效地控制了污染物排放量,在优先保护水环境的前提下最大化水资源利用效益。

图3 讨价还价博弈模型、主从博弈模型与多目标模型的结果比较
4 结论
本文针对决策冲突主体之间难以达成有约束力的合作协议情况,提出水资源利用与排污控制的非合作博弈方法,从博弈模型方法上深入分析博弈主体获得纳什均衡解的协商过程与交互过程,研究讨价还价博弈与主从博弈的均衡解、多目标优化的非劣解之间的关系与内涵。解决先行用水给后续排污带来的负外部性问题,实现水环境保护优先的前提下发展水资源经济。主要研究结论如下:(1)建立水资源利用与排污控制的讨价还价博弈模型,结合一致后退讨价还价法方法求解模型,求解过程清晰高效,通过平等的协商方式体现了博弈主体的协调过程与决策行为。(2)构建水环境保护主体与水资源利用主体的上下级层次结构,建立主从博弈模型,采用双层模糊优化方法求解模型,通过控制-响应-协调方式体现分层次利益主体之间的行为次序与交互特性。(3)对比分析了讨价还价博弈、主从博弈与传统多目标优化模型解的内涵与关系。讨价还价博弈与主从博弈模型的均衡解都在多目标优化模型的非劣解前沿上,说明非合作博弈方法不仅强调了个体利益,还兼顾了整体利益。而且讨价还价博弈的均衡解有效缩减了非劣解范围,主从博弈的唯一均衡解更有效地控制了污染物排放量。
非合作博弈方法为我们了解水资源利用中行为主体之间的互动行为、冲突与合作提供了一个强有力的解释和分析工具。文中非合作博弈方法中博弈主体具有一定主观能动性、在解决实际问题中博弈主体的策略选择偏好,模型参数的动态变化、可供水量与需水的不确定性影响,需要进一步深入探讨和研究。

