排水期沟渠附近潜水非稳定流解析解及参数反演
任红蕾,陶月赞,林 飞,韦 婷
(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)
1 研究背景
在地下水渗流力学中,受第一类边界(如河渠水位)条件控制的一维潜水非稳定渗流模型,是最基本的经典模型之一[1-4],是灌排沟渠工程设计[5]、水文过程分析与水资源量评价[6-9]、排水工程附近地下水动态过程分析[10-11]等研究的重要理论工具。近年来,一维潜水非稳定渗流模型进一步拓展到其它研究中,如水岸生态工程设计中的地表水与地下水之间的水量交换过程评价[12-13]、滨海含水层保护工程设计中的地下水水位对海水位及潮汐的响应分析[14]。
关于这类经典模型解析解问题的研究,多关注含水层接受补给影响的河渠类水位边界[15-18],对仅能接受含水层排泄的排水沟渠类边界多侧重数值解[11,19],而少见有解析解研究文献。在河渠类水位边界附近非稳定渗流模型解析解问题研究中,多未考虑降水入渗补给、灌溉回归和潜水蒸发等潜水含水层垂向水量补排作用[1-4,15-16],并在假设河渠边界水位瞬时上升ΔH且保持不变[1-4]或在对变化水位适当处理[15-16]的条件下,讨论模型的解及其应用。在同时考虑边界与垂向水量补排作用的文献中,文献[17]对于时变的潜水含水层垂向水量交换强度ε(t),依据ε(t)为常数时模型的解,对ε(t)进行离散,采用叠加方法获得时变问题的解;文献[18]讨论了依据解求算模型参数的方法。
潜水位动态的计算与预测,是农田灌排水渠系设计等实际问题研究的理论基础。潜水具有自由水面,通过包气带可与外环境直接相联通,潜水蒸发、降水入渗补给、灌溉回归等潜水含水层的垂向水量补排作用在潜水水位动态研究问题中往往难以回避。
排水期间沟渠水位特征有别于河渠,为保证排水效率,排水期间沟渠水位一般不会有较大幅度上升,如淮北平原沿淮地带,潜水水位埋深较浅,普遍设置排水大沟调控地下水水位,排水大沟设置有滚水坝[19]以控制排水水位。在潜水蒸发和潜水向沟排泄的共同作用下,农田区的潜水水位缓慢下降,但沟中水位在滚水坝控制下基本维持不变。这一过程,可能持续数天甚至数十天,此时沟渠水位显然是稳定水头(水位高度为滚水坝坝顶高度)边界。
数学模型的解析解,是问题机理研究、变量间关系定量分析的重要工具。就第一类边界附近的一维潜水渗流模型而言,随着源汇项和边界条件函数形式的变化,模型求解方法与过程、解的表达形式与应用方法都有很大变化[15-18]。因此,准确概化模型的边界条件和初始条件,对解的适用性有着重要作用。
结合上述实际,根据现行降水量、蒸发量等观测制度,将垂向水量交换强度ε(t)离散成逐日变化的阶梯函数,建立沟渠水位“稳定不变”的边界条件下、含阶梯函数型源汇项ε(t)的潜水非稳定渗流模型。对模型中Boussinesq 方程,采用第一线性化方法,通过Laplace 变换得到模型解析解,并对解析解进行数值验证,讨论其物理意义。根据解析解反问题研究思路,建立模型参数求算方法,相对文献[17-18],边界条件更加符合实际,垂向水量交换强度处理方法及模型求解过程更为严谨,模型的解也相对简洁、应用方便。
2 渗流模型
2.1 数学模型一顺直沟渠,如图1,其所处地段的水文地质条件,可概括为:

图1 沟渠附近潜水渗流场示意
①一侧为沟渠边界的孔隙潜水含水层均质且各向同性、隔水底板水平,在水平方向上无限延展;
②沟渠在边界处完整切割潜水含水层,潜水水流可视为一维流;
③潜水初始水位h(x,0)与沟渠水位一致,呈水平状态;
④沟渠水位在研究期内保持不变,可视为一类边界;
⑤垂向水量交换强度ε(t),在研究区域内各处相等。
该问题的数学模型可写成模型(Ⅰ):
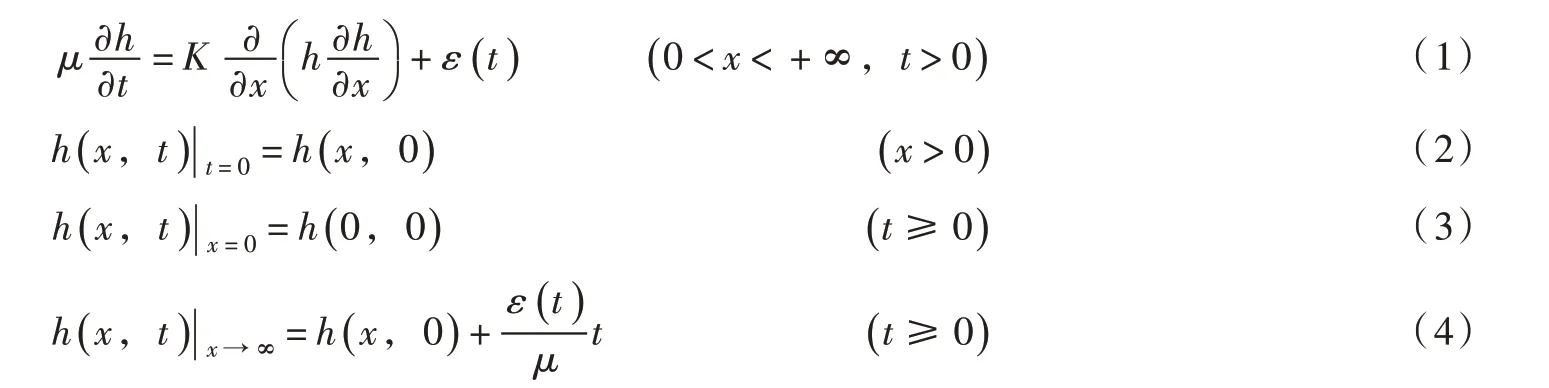
式中:μ为潜水含水层的给水度;K为潜水含水层的渗透系数,m/d;h为潜水水位,m;ε(t)为垂向水量交换强度,m/d;x为计算点距边界的距离,m。
在经典的J.G.Ferris 模型[18]中,上述水文地质条件中的条件④为“河渠水位迅速升高△H后、水位保持稳定不变”,而模型(Ⅰ)是“沟渠水位在研究期内保持不变”;另外,模型(Ⅰ)在J.G.Ferris 模型基础上,增加了条件⑤。
2.2 垂向水量交换强度的离散农田或边坡所在地段的潜水含水层,多在野外直接出露于外环境,可形成的垂向水量交换项有灌溉回归、降水入渗补给、潜水蒸发等,相关观测和统计的变量,对应有灌溉量、降水量、水面蒸发量,这在实际工作中都是按时间步长为一日进行观测统计的,因此,依据观测资料给出的垂向水量交换强度ε(t)一般也是逐日量,即,ε(t)是一个时间步长为一日的阶梯函数(也称分段常值函数)。对于评价期内随时间变化的垂向水量交换强度ε(t),令评价期为n段,第i段时间为ti-1~ti,对应的垂向水量交换强度为εi。εi为正,表示补给含水层;εi为负,表示排泄含水层。采用“叠加法”将ε(t)写成阶梯函数形式:
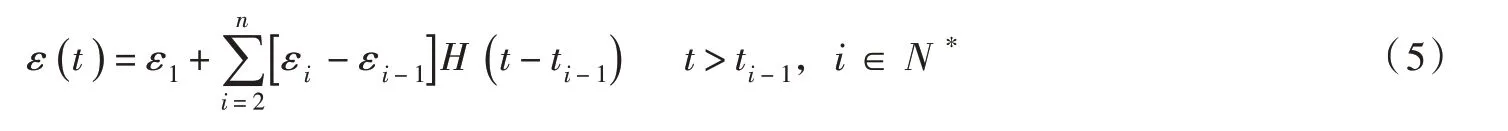
式中:ε1为第1 个时段(即t0~t1时段)内对应的垂向水量交换强度,m/d;H(t-ti-1)是Heaviside 函数,当t<ti-1时、H(t-ti-1)=0,当t≥ti-1时、H(t-ti-1)=1。
2.3 模型求解在模型(Ⅰ)中,当h(x,t)-h(x,0)≤0.1hm(hm为潜水含水层的平均厚度,这在解决实际问题的过程中基本可以满足[15-18])时,可以采用Boussinesq 方程第一线性化方法,令u(x,t)=h(x,t)-h(x,0)。
对模型(Ⅰ)求关于t的Laplace 变换,注意阶梯函数Laplace 变换的性质L[ε(t)]=ε(t)/s[20],L[ε(t)]是关于ε(t)的Laplace 算符,可得模型(Ⅱ):

式中:a=Khm/μ,a为导压系数,m2/d;s为Laplace 算子;uˉ为u关于t的Laplace 变换过程中的象函数。
模型(Ⅱ)中的式(6)是二阶常微分方程,由该二阶常微分方程的通解,结合边界条件式(7)、式(8),可获得模型(Ⅱ)的特定解:

对式(9)进行Laplace 逆变换,[f(t)]/s项求逆变换时,注意Laplace 变换中的“积分性质”,即:

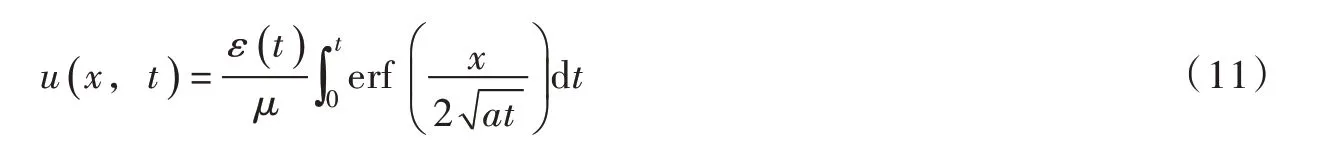
式中er(fz)为误差函数,。
因为u(x,t)=h(x,t)-h(x,0),并将式(5)代入式(11),结合Heaviside 函数的性质,可得:
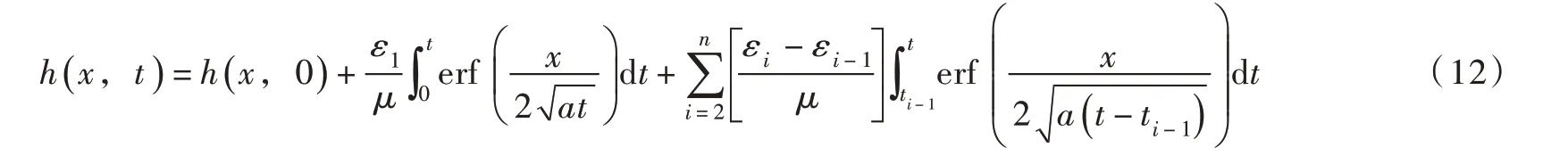
式(12)即为模型(Ⅰ)的解,也即水位“稳定不变”沟渠边界条件下、含时变垂向水量交换项ε(t)的潜水非稳定渗流模型的解,同时也是文献[18]的解在△H=0 时的特例。
2.4 解析解的数值验证在研究河渠附近一维潜水非稳定渗流问题时,针对不同的实际问题,Zissis和Bansal 等通过Laplace 变换方法,得到了一维线性化形式的Boussinesq 方程的解析解,利用MacCor⁃mack 显式差分方案对解析解进行了数值验证[21-23]。MacCormack 格式是一种求解可压缩流体流动问题的显式有限差分格式,在时间和空间上具有二阶精度[21-29]。
本文利用Laplace 变换法求解了线性化的Boussinesq 方程,得到了含时变垂向水量交换项ε(t),水位“稳定不变”沟渠边界条件下潜水非稳定渗流模型的解,为了验证线性化方法的有效性和解析解的可靠性,通过上述研究中MacCormack 格式的有限差分法计算相应非线性方程式(1)的数值解,并将解析解与数值解进行比较。假设n时刻各节点的水位hk,n均已知,利用MacCormack 格式的预测校正两步法进行时间推进,求解出n+1 时刻各个节点的水位hk,n+1。首先,在预测中对空间导数进行向前差分,得到用正向差分代替时空导数得到h的预测方案[21-23],如下:
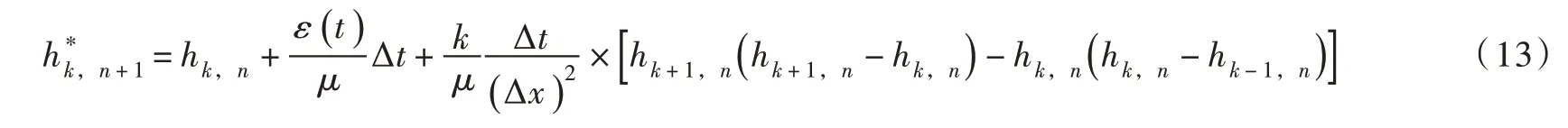
第二步,对x的偏导数用后向差分近似代替,而对于t的偏导数用正向差分近似代替,方程式(1)可写为[21-23]:

最终,hk,n+1的修正值为和的算术平均值[21-23]:
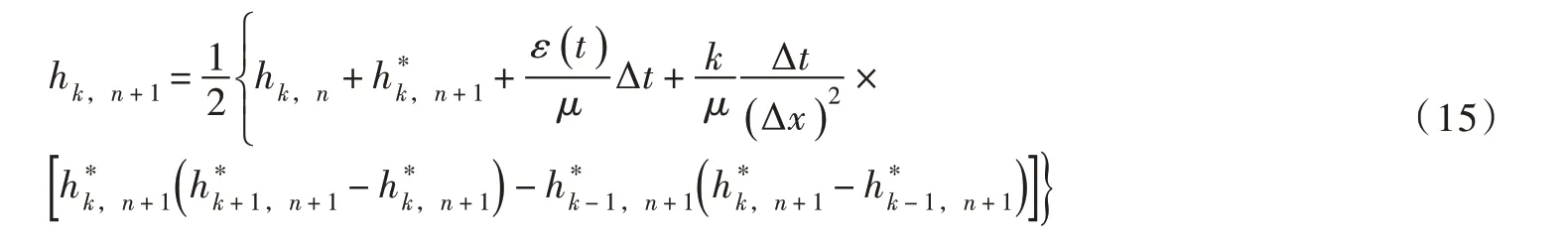
上述式(13)—(15)构成了非线性方程式(1)的MacCormack 格式的有限差分法计算方案,其稳定准则为[21-23]:

根据式(12)—(16),参考淮北平原区域的水文地质特征,模型选取粗砂、中砂、细砂三种含水层介质,给水度分别设为0.30、0.22 和0.17[30],渗透系数分别设为30 m/d、20 m/d 和7 m/d[30],初始潜水位取27.000 m,潜水含水层平均厚度取3.5 m。计算期为5 天,假设:第一天、第二天为降水入渗阶段,对应的降水入渗补给强度分别设为0.050 m/d 和0.030 m/d;后三天为潜水蒸发阶段,潜水蒸发强度均设为0.001 m/d。利用以上参数,24 h和48 h时的潜水位及相对误差计算结果分别如图2、图3所示。
由图2 和图3,在不同的水文地质参数条件下解析解与数值解的吻合度都比较好,相对误差最大不超过0.15%,表明推导解析解过程中的线性化方法是有效的,并验证了模型解析解的可靠性,同时也说明了将垂向水量交换强度ε(t)离散成时间步长为一日的阶梯函数的方法是可行的。
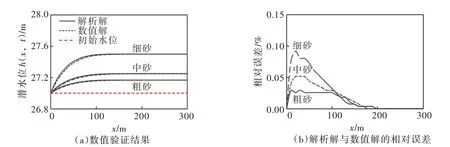
图2 t=24h 时的潜水位解析解与数值解计算结果及相对误差

图3 t=48h 时的潜水位解析解与数值解计算结果及相对误差
在离沟渠边界30 m 和300 m 处虚拟两个潜水位观测点,分别研究其潜水位变化过程,计算结果如图4所示。沟渠边界与垂向水量交换(前两天的降水入渗及之后的潜水蒸发)共同作用下,降水入渗阶段潜水位上升,导致潜水位高于沟渠水位而向沟渠排泄,与远处水位观测点(x=300 m)相比,近沟渠边界观测点(x=30 m)的潜水位上升速度较慢;潜水蒸发阶段,近沟渠边界点的潜水位下降速度较快,这表明,沟渠边界对潜水位的影响作用随x增大而减小。由图4 及式(12),对于计算域内任意点x,潜水位h始终是随时间t变化的,计算期间计算域内的潜水位始终保持非稳定状态,这符合潜水非稳定渗流理论的基本特点。

图4 距沟渠边界的距离分别为30m 和300m 处的潜水位变化过程
2.5 特定解及其物理意义
(1)当x→0 时
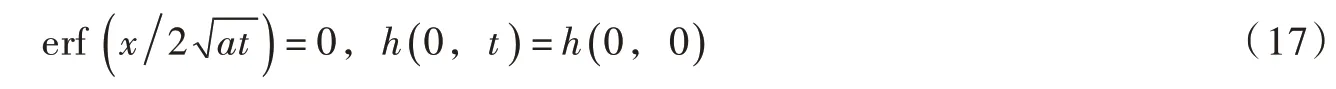
此时,对应的是边界处的潜水位与沟渠水位等高,这符合地下水渗流力学中的基本原理。
(2)当x→∞时

则有:

此条件下,对应的是距离边界无穷远处的潜水水位与沟渠边界无关,即模型(Ⅰ)中x→∞时的边界条件。实际中,一般离边界较远距离时,沟渠对潜水水位的影响就基本可以忽略。
(3)当n=1 时

此条件下,计算期内ε1为恒定常数,这也是文献[17]在ΔH=0 条件下这类模型的基本解。
3 含水层参数求算方法
根据地下水位监测数据求解含水层参数,是沟渠附近潜水非稳定渗流理论和模型研究的重要应用之一。直接体现在式(12)中的参数有a、μ,通过a和μ之间的关系,还隐含着渗透系数K=μa/hm。
通常情况下,根据野外常规试验,可以得到参数μ的值,利用非稳定渗流模型,目的是为了求解参数a。关于正问题研究方法,一般在给定参数初值的条件下,利用解计算出水位或水位变动速度值,将计算值与实际值拟合,通过不断试算,以确定参数值,这一试算过程显然比较繁琐。因此,可利用反问题研究思路,建立相应的求解方法。
令:

利用n=1 时段的水位动态数据,由式(12),得:

式中φ(x,t)为潜水位变动速度。
3.1 拐点法由式(21),可得:

由式(22),得:


当然,只有n=1 时段足够长,才能出现拐点。实例研究表明,出现拐点的时间小于24 h,这在实践中可以满足。
3.2 配线法由式(21),对于一个到边界直线距离为x的观测孔,z=x/2(at)1/2,首先建立不同a值对应的er(fz)~t曲线图作为理论曲线图族。再由实测潜水水位,制出曲线,该曲线应该可以同erf(z)~t理论曲线图族中的某条曲线完全重合,仅相差ε/μ倍,此时,两条曲线所对应的a值相等。因此,根据该观测孔潜水水位实际观测数据,通过配线法,可直接确定含水层参数a的值(如图6)。
4 实例研究
安徽省境内淮北平原近淮河地段,潜水含水砂层埋深为5 ~ 6 m,底部为不完全连续黏性土层。现状条件下,该地段潜水埋深多为1.5 ~ 3.0 m,潜水蒸发(该地段潜水极限蒸发深度为4.8 m[31])、降水入渗等垂向水量交换作用对潜水位动态影响明显。研究区内明沟排水系统中,排水大沟设计深度为5 m,基本完全切割潜水含水层,相邻大沟之间的距离约为2 km[32-33]。受渠首滚水坝控制,排水过程中沟渠内的水位基本保持不变。2009年7月11日和12日,产生了一次时程分配比较均匀的连续降雨,在此之前,已存在很长一段时间内连续无降雨的情况,11日、12日的日降雨量分别为86 mm、74 mm,降雨前后,沟渠的水位没有变化。在离沟渠直线距离65 m 处有一口地下水位观测井(自记式),潜水位随时间的变化过程见表1。平均降水强度为80 mm/d,根据区域研究成果,降水入渗补给系数取0.20,降水入渗补给强度为16 mm/d。
(1)拐点法求导压系数a。由表1 中的地下水位监测数据,用向前插值法计算和,按时间间隔为6 h 进行摘录,曲线在18~21 h 之间出现拐点,因而,该时段内摘录的时间间隔加密至1 h。相关数据和求解过程见表1,计算得到的曲线变化过程见图5。

图5 拐点法求tg的过程
据上述有关基础数据与拐点时间:x=65 m,tg=19.5 h,由式(24),可求出a=865 m2/d。
(2)配线法求导压系数a。计算过程中,μ通过野外实测数据获得,μ的值为0.035。由表1 中的数据,计算出的φ(x,t)~t曲线与x=65 m 处的er(fz)~t理论曲线图中的曲线组配线。根据观测数据得到的φ(x,t)~t曲线处于a值为800 m2/d 和1000 m2/d 的理论曲线之间,并靠近a值为800 m2/d 的理论曲线(见图6)。由此,含水层参数a可取为850 m2/d,这同拐点法的计算结果仅相差1.73%。

图6 配线法求a 的过程
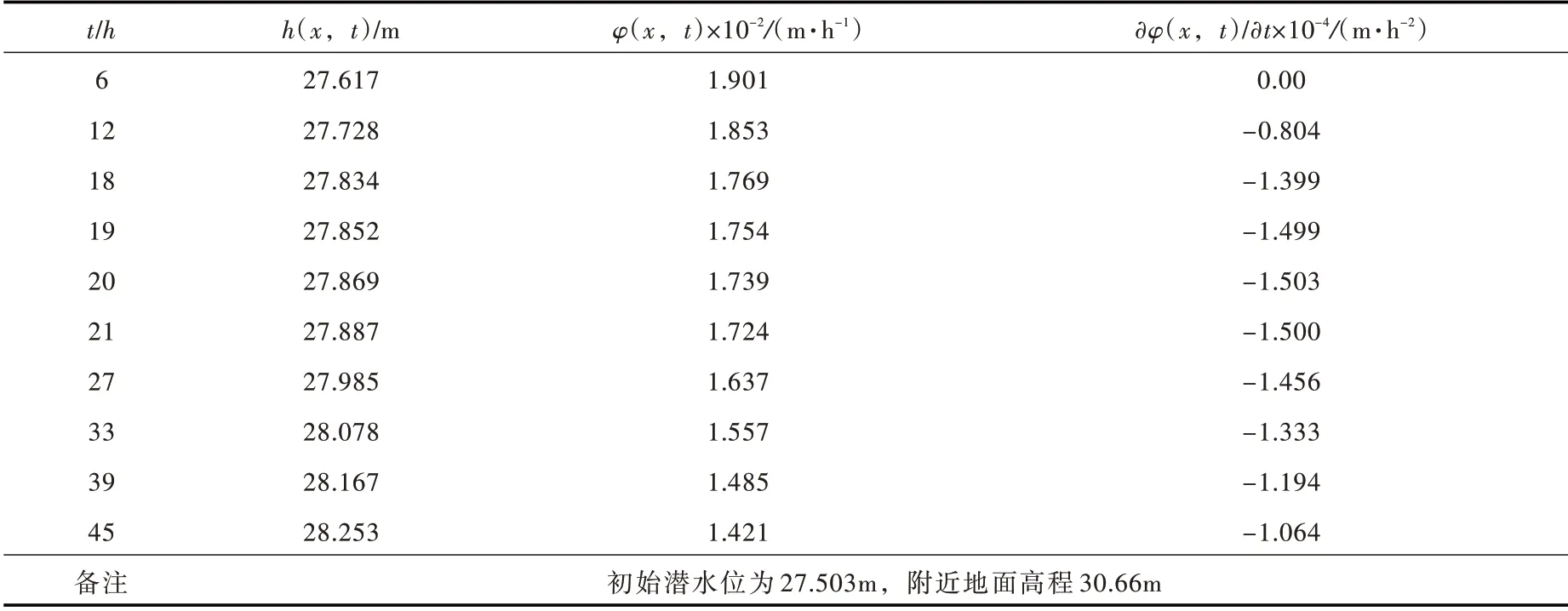
表1 x=65m 处地下水位动态监测数据(2009.7.11—2009.7.12)与整理
理论曲线族绘制过程中,可根据实际计算精度要求对理论曲线进行加密,从而提高配线法求解导压系数的精度。
(3)参数反演结果的合理性分析。通过数值法验证了模型解析解式(12)的可靠性,因此可将上述计算得到的导压系数a的值代入式(12),计算x=65 m 处不同时刻的潜水位,并与实测值进行比较,如图7所示。

图7 x=65m 处潜水位解析解与实测值对比结果
对比分析,当a=865 m2/d 和a=850 m2/d 时,x=65 m 处潜水位的解析解与实测值都非常接近,表明拐点法和配线法求算导压系数a的方法是合理、可靠的。
5 结论
在类似淮北平原沿淮潜水位埋深较浅的区域,沟渠附近的地下水水位变动,不仅与灌溉回归、降水入渗补给、潜水蒸发等垂向水量交换作用有关,而且受沟渠等排水工程影响明显。在研究垂向水量补排作用下沟渠附近潜水非稳定渗流模型的过程中,形成以下主要结论:
(1)在潜水位埋深较浅的区域,用于控制潜水位的排水沟渠,对潜水水位消退变化的影响显然有控制性作用,通常潜水蒸发、降水入渗补给等垂向水量补排作用也不可忽视,此条件下,宜将这两者统一纳入数学模型中。
(2)对于有滚水坝调节控制的沟渠,在自由排水期间,沟渠内的水位一般保持稳定不变。根据实际观测统计制度,潜水蒸发、降水入渗补给等垂向水量补排作用强度,宜概化为逐日变化的阶梯函数。
(3)利用模型解反问题研究思路,根据潜水位变动速度随时间的变化规律,建立拐点法、配线法求模型参数的方法,直接简明;利用文中模型的解,通过反问题研究方法,也可建立依据潜水位变动速度计算垂向水量交换强度的算式。
(4)值得指出的是,实际工作中,大范围农田排水往往设置有多条平行排水沟渠,本文方法适用于沟渠相距足够远的情形;当沟渠相距较近并对地下水水位有叠加影响时,属两侧都是一类水位边界控制下的潜水非稳定流问题,此情形下问题求解方法不同于本文方法,值得进一步研究。

