水工高性能混凝土配合比多目标智能优化设计与分析方法

任秋兵，李文伟，李明超，杨 琳，张梦溪，沈 扬

（1.天津大学 水利工程仿真与安全国家重点实验室，天津 300354；2.中国长江三峡集团有限公司，北京 100038）

1 研究背景

高性能混凝土（high performance concrete，HPC）因具有高强度、高工作性和高耐久性等特点而被广泛用于高速公路、高层建筑和水利枢纽工程中［1］。近年来，随着我国基础设施建设的不断推进，对HPC 不同特性（如力学性能、经济性和环保性等）的综合需求愈来愈高，部分需求甚至超出了现行标准/规范［2-3］。例如，三峡主体工程混凝土要求在满足设计技术指标及施工需求的前提下，具有较高的耐久性、抗裂性、低热性、体积稳定性、良好工作性和经济合理性［1，4］。加之，HPC 材料配比复杂、结构组分多样，普通混凝土制备方法难以指导多目标需求下的HPC 配合比设计［5-6］。因此，研究能够满足多目标需求的HPC 配合比优化设计方法具有十分重要的理论与实践意义。

为实现高效、准确的HPC 配合比设计，国内外学者在数值计算优化方面进行了大量有益的探索。Sobolev［7］根据试验数据推导了抗压强度和坍落度的经验公式，并将其用于制备28 d 抗压强度介于50 ～ 130 MPa 的HPC。季韬等［8］提出了基于最少浆体理论的混凝土配合比优化方法。王帆［9］发展了一种基于比强度的HPC 配合比设计方法。哈娜［10］应用线性规划法优化确定符合施工性能要求的HPC 配合比参数。Ferdosian 等［11］证实了响应面法在HPC 配合比优化设计中的适用性。此外，以全计算法、致密体积法、最佳砂率模型为代表的半定量或定量方法也促进了混凝土配合比设计的解析化与自动化［12］。尽管这些方法对优化HPC 配合比发挥了重要作用，但仍存在着设计变量偏少、人工参与度较高、难以充分利用积累的配合比试验数据等不足。

人工智能作为先进的数据驱动方法，在混凝土配合比设计中的应用已成为当下的研究热点［13-15］。一方面，得益于强大的数据挖掘能力，智能回归算法能够准确表征混凝土性能与配合比参数之间的非线性映射关系［16］。例如，陈庆等［17］、Nguyen 等［18］采用人工神经网络建立了适用于不同龄期的HPC抗压强度预测模型，均取得了较好的预测效果。也有学者通过随机森林［19］、梯度提升树［20］等集成方法来进一步提高模型的预测精度。另一方面，群智能优化算法具有较强的全局搜索能力，且易于实现，在求解配合比优化设计问题方面表现出明显优势［21］。例如，陈晓东等［22］、Cheng 等［23］、徐毅慧［24］、Parichatprecha 等［25］将遗传算法用于推算HPC 的理论最优配合比，结果表明，优化后的HPC各项性能指标均满足要求，单方造价也大为降低。

但是，在HPC 性能预测方面，多数模型是基于小数据集（一般不超过100 组试验数据）建立的，少量训练样本涵盖的数据信息有限，容易导致模型过拟合。而在HPC 配合比优化方面，已有研究大都只考虑了单一目标（抗压强度或经济性），无法充分考虑不同性能指标之间的关联性，这极大地限制了其应用范围。针对上述问题，本文开展多目标需求下的HPC 配合比智能优化设计研究，其主要包括以下4 个方面的内容：（1）建立试验数据库。广泛收集不同工程的HPC 配合比数据及各项性能试验资料，整理汇编形成HPC 配合比试验数据库。（2）构建智能预测模型。随机森林算法具有精度高、稳定性强、不易过拟合（即泛化能力好）等特点［26］，被用于建立混凝土抗压强度与各组分材料掺量之间的数学关系。（3）多目标联合优化。以抗压强度、经济性和环保性为优化目标，建立HPC 配合比多目标优化数学模型，并引入自适应进化多目标粒子群优化算法进行求解，获得Pareto 解集。（4）配合比参数优选。由于多目标优化算法得到的最优解不存在唯一性，需根据技术规范和实际需求从Pareto前沿中选取一个解作为最优配合比。

2 配合比试验数据库

从文献［27-30］总共收集到1133 组HPC 配合比试验数据，统计信息见表1。这些HPC 试件具有不同用量的水泥、高炉矿渣、粉煤灰、水、减水剂、粗骨料和细骨料，养护龄期从1 d 到365 d 不等，保证了训练样本的丰富性和多样性。所有的抗压强度数据都是在高30 cm、直径15 cm 的标准圆柱体试件上遵循标准化流程测定的，未经过放缩处理。根据算法规则，需将试验数据按照9∶1 的比例随机划分成训练集和测试集，前者用来构建HPC 抗压强度预测模型，后者则用来评价模型性能的优劣。

表1 HPC 配合比试验数据统计信息

3 配合比智能优化设计方法

3.1 配合比-抗压强度映射表征随机森林（random forest，RF）是由Bagging 方法和随机子空间方法相结合而形成的一种高效、并行式的集成学习算法［31］，其基本组成单元是决策树。它利用Bootstrap 重抽样方法从原始训练集D中抽取k个样本子集并对每个Bootstrap 样本子集进行决策树建模，然后组合多棵决策树的预测值，通过投票表决得到最终的预测结果。算法流程如图1所示。其中，每棵决策树都选择部分样本及部分特征，一定程度上能避免模型过拟合；每棵树随机选择样本并随机选择特征，使模型具有较好的抗噪能力，且性能表现稳定。

图1 随机森林算法流程

为了表征HPC 配合比参数与抗压强度之间的复杂映射关系，将水泥用量（q1）、高炉矿渣用量（q2）、粉煤灰用量（q3）、拌合水用量（q4）、减水剂掺量（q5）、粗骨料用量（q6）、细骨料用量（q7）和养护龄期（t）作为输入变量，构建了基于随机森林算法的HPC 抗压强度智能预测模型，表达式如下：

式中：f(×)为随机森林算法；CCSt为不同龄期的HPC 抗压强度；随机特征数目Mtry和决策树棵数Ntree是影响随机森林模型性能和效率的两个重要参数，Mtry值控制了随机森林模型属性的扰动程度，Ntree值会影响模型的训练程度和预测精度，两者均可通过试错法来确定。

3.2 多目标联合优化数学模型对HPC 而言，28 d 抗压强度是衡量其力学性能的重要指标，控制其经济成本和碳排放量又是工程建设的现实要求。鉴于此，本文以抗压强度最大、单方成本最低和碳排放量最少为研究目标，结合原材料及性能指标相关限制，建立综合考虑力学性能、经济性和环保性的HPC 配合比多目标优化数学模型，包括目标函数集和约束条件集两部分。

（1）目标函数集。构造目标函数集的关键是建立HPC 的抗压强度、单方成本和碳排放量与配合比参数（即设计变量）qi，i=1，2，…，7之间的数学关系。大量研究成果［22-25，32］表明，抗压强度与材料组分之间呈高度非线性关系，而单方生产成本和碳排放量与配合比参数一般呈线性关系。因此，HPC 的抗压强度目标函数采用前述随机森林智能模型表征，单方成本和碳排放量的目标函数则由线性函数表征，公式如下：

式中：Opt(×)为优化目标函数；CCS28为28 d 抗压强度；MPC为单方混凝土生产成本；ci，i=1，2，…，7依次为水泥、高炉矿渣、粉煤灰、水、减水剂、粗骨料和细骨料的单价；MPC0为单方混凝土的平均拌合、运输成本，通常随混凝土生产规模的扩大而降低；CDE为单方混凝土产生的碳排放量；ei，i=1，2，…，7为各材料组分的单位产出能耗值；CDE0为拌合楼、运输工具等机械设备产生的碳排放量，一般随混凝土总方量的增大而增加。为了便于计算，文中MPC0和CDE0均取常数（MPC0=15，CDE0=5）。

（2）约束条件集。配合比优化设计是建立在满足规范和工程设计要求（即约束条件）的基础上的。同时，增加约束条件有利于缩小搜索范围，加快优化求解速度［33］。本文将约束条件细分为映射关系约束、单方体积约束、原材料用量及比率约束与目标函数值约束4 类，前两者属于等式约束，后两者属于不等式约束。其中，映射关系约束即是配合比-抗压强度关系式，该关系以训练好的随机森林模型表达。单方体积约束（以1 m3计）则由下式表征：

式中：CV为HPC 中各材料组分的总体积；ui，i=1，2，…，7依次为水泥、高炉矿渣、粉煤灰、水、减水剂、粗骨料和细骨料的密度。

不等式约束条件源自设计规范或以往经验对原材料用量、相关参数比率和各项性能指标的最大、最小值的若干限定，采用下式统一表征：

3.3 模型求解方法对于不同的混凝土配合比，单方HPC 所产生的碳排放量会有较大差异，同时由于各组分之间的交互影响，使得HPC 的力学性能与生产成本也会大不相同。在许多情况下，28 d 抗压强度最大化、单方成本最低化与碳排放量最少化3 个目标甚至存在冲突，难以找到一个解使得所有目标同时达到最优。因此，如何在保证HPC 抗压强度达到设计要求的前提下，最大限度地降低生产成本，减少碳排放量将是一个复杂的多目标、多变量联合优化问题。针对此问题，本文提出利用自适应进化多目标粒子群优化算法（adaptive evolutionary particle swarm optimization，AEPSO）［34］求解上述数学模型。

多目标粒子群优化算法（MOPSO）因寻优能力强、收敛速度快和设置参数少等优点，同时一次运行可得到多个解，且能逼近非凸或不连续的Pareto 最优前沿，因而被认为是求解多目标优化问题最具潜力的方法之一。本文选用的AEPSO 在传统MOPSO［35］的基础上做了如下改进：（1）采用非支配排序策略和动态加权法选择最优粒子，引导种群飞行，以提高Pareto 解的多样性；（2）运用自适应惯性权重来提高全局搜索能力；（3）当种群的搜索能力减弱时，利用变异操作来引导粒子群跳出局部最优。通过实例验证，AEPSO 能够在保证优化解多样性的同时具有更好的收敛性和稳定性。此外，为了使AEPSO 能够求解带约束的多目标优化问题，本文采用罚函数法来处理模型约束条件，其基本原理和实现过程详见文献［36］。

3.4 配合比智能优化设计流程基于上述配合比试验数据库与多目标联合优化数学模型（含目标函数及约束条件体系）的构建，提出了多目标需求下的HPC 配合比智能优化设计方法，其实施流程（见图2）包括以下步骤。

图2 HPC 配合比智能优化设计流程

（1）步骤1。根据工程建设对HPC 配合比设计的多目标需求（即力学性能、经济性和环保性），确定设计变量Q和约束条件，同时建立单方生产成本和碳排放量的目标函数。

（2）步骤2。利用训练集构建基于随机森林算法的28 d 抗压强度预测模型，并用测试集对建立的随机森林模型进行误差分析，若不满足精度要求，则需增加试验数据量，重新训练模型；若满足要求，则直接作为力学性能的目标函数。

（3）步骤3。从当前配合比试验数据库中筛选出满足约束条件的所有配合比，记为。

（4）步骤4。采用AEPSO 算法求解HPC 配合比多目标联合优化数学模型，获得的Pareto 前沿即是优化设计出的候选最优配合比，记为。

①初始化种群中各个粒子的位置和速度，并设置初始种群P，群体规模N，迭代次数I和最大允许速度Vmax。

②评价当前种群P中所有粒子的各目标值（即适应度值）。

③按照动态加权和非支配排序的策略更新种群P中各个粒子的个体最优位置pi和全局最优位置pg。

④通过引入自适应惯性权重和变异操作，计算各粒子新的位置和速度，并重新计算每个粒子的各目标值。

⑤以所得粒子是否接近全局最优解作为收敛准则，若未达到收敛，则返回步骤②，继续更新种群；若收敛，则输出种群P作为Pareto 解集。

（6）步骤6。结合现行规范和设计要求，对上述设计出的理论最优配合比Q *进行试拌、调整，最终得到实际使用的最优配合比Q **。

（7）步骤7。将Q **的试验结果添加到当前数据库中，丰富配合比试验数据，以实现知识的不断累积。

4 实例分析

结合某工程实例，验证本文提出的HPC 配合比智能优化设计方法的可行性与有效性。已知该工程所用HPC 的设计要求如下：28 d 抗压强度应介于30 与40 MPa 之间，单方生产成本应低于520 元，单方生产碳排放量应少于200 kg，各材料组分的用量限制和相关参数比率的允许范围分别见表2、表3。根据当地条件，表2 列出了各种原材料的必要属性（密度、单价和单位产出能耗值）。由于原材料的来源稳定（即供应厂家、料场较为固定），其质量特性可认为基本保持不变，只需考虑用量的影响。基于上述信息，按照3.4 节中的设计流程对HPC 配合比进行优化。

表2 HPC 各材料组分的必要属性和用量限制

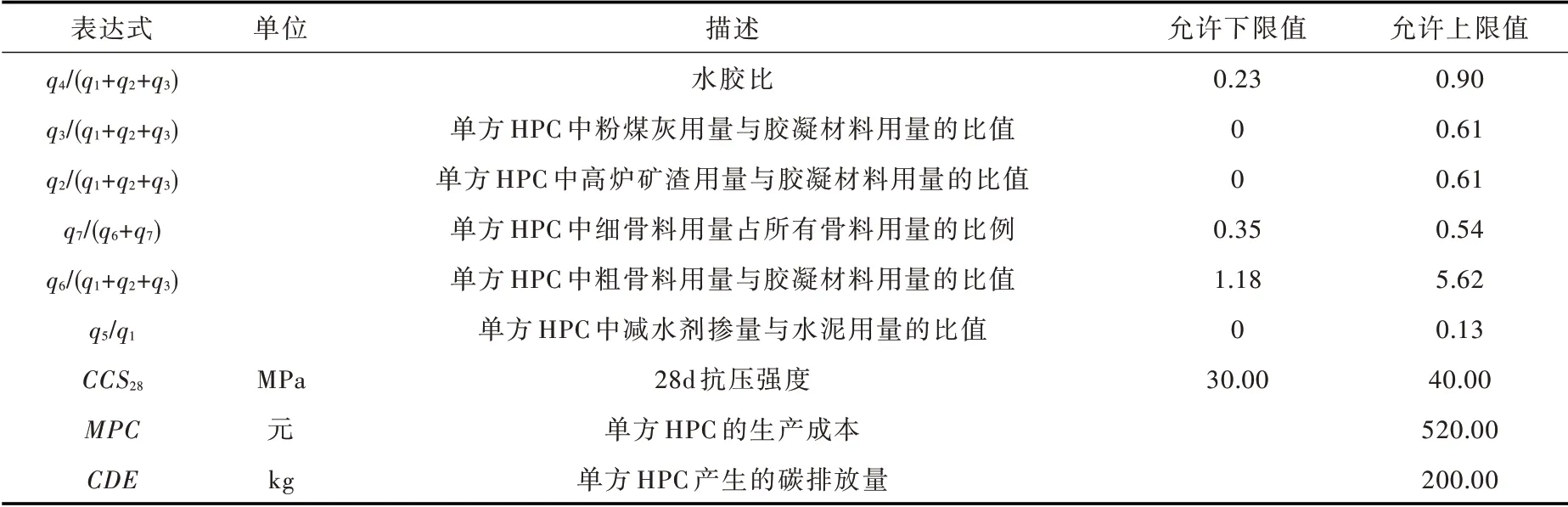
表3 相关参数比率允许范围与目标函数值的约束条件

4.1 抗压强度预测模型误差分析为兼顾抗压强度预测模型的精度与效率，采用试错法优化了随机森林算法的两个控制参数，分别取Mtry=2，Ntree=280。该模型在训练集（1020 组数据）和测试集（113组数据）上的预测表现如图3所示。模型性能用相关系数（correlation coefficient，R）、均方根误差（root mean squared error，RMSE）和平均绝对误差（mean absolute error，MAE）［30］3 个指标定量评价。R值越接近于1，RMSE和MAE值越小，表示模型性能越好。由图3 可知，抗压强度预测值与实测值之间呈现强相关关系（R值在0.95 以上），即随机森林模型对于HPC 抗压强度的预测精度较高（RMSE和MAE值均较小）。

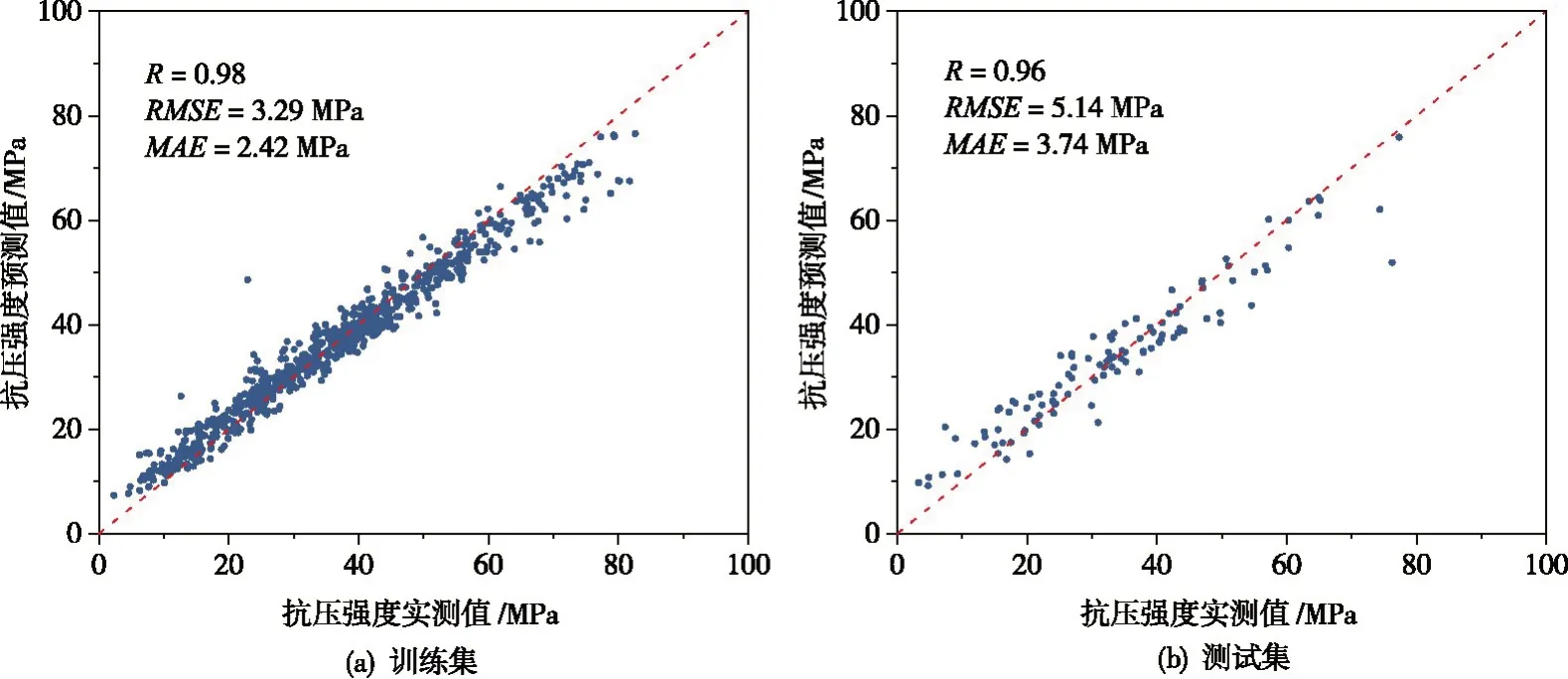
图3 随机森林智能模型的抗压强度预测性能

为进一步验证基于随机森林算法的HPC 抗压强度预测模型的性能优势，将其与文献报道的其他方法进行了比较。对比方法包括多基因遗传规划（M-GGP）模型［38］、人工神经网络-支持向量回归（ANN-SVR）集成模型［39］和智能萤火虫算法-最小二乘支持向量回归（SFA-LSSVR）混合模型［40］。表4列出了不同模型在测试集上的预测效果。从表4 可以看出，随机森林模型的R值最大，达到0.96，且RMSE 和MAE 值均小于其余3 种方法，表明随机森林算法在抗压强度预测方面具有明显的优越性。由此可见，随机森林智能模型能够准确表征原料配合比与抗压强度之间的非线性关系。

表4 测试集上不同模型的预测性能对比

4.2 多目标优化模型的求解结果将表2、表3 中相关数据代入式（2）—式（5），即可得到HPC 配合比多目标优化数学模型的表达式。根据约束条件集从当前数据库中筛选出满足要求的全部配合比（共24组），如表5所示。随后按照3.4 节中步骤4 所述流程，使用AEPSO 算法对此数学模型进行求解，其中群体规模N=100，迭代次数I=250。图4 为经迭代优化后得到的Pareto 前沿散点分布图，总计60 个Pareto 解（即60 组候选最优配合比）。从图4 可以看出，Pareto 前沿分布均匀（多样性较好），收敛性也较好。此外，抗压强度、单方生产成本和碳排放量两两之间存在明显的相互制约关系，难以同时达到最优，体现出HPC 配合比设计考虑多目标优化的必要性。

表5 当前数据库中满足设计要求的24 组配合比参数

为了验证优化结果的合理性，随机选取3 组配合比进行试拌物理试验，对比结果见表6。从表6可以看出，按照优化配合比制备的HPC 的试拌实测强度与其计算强度之间的误差较小，最大仅为3.92%，说明经过配合比优化后的HPC 抗压强度与设计给定值相近，没有产生强度冗余或不足。

表6 优化结果试拌验证

4.3 不同偏向的配合比参数优选在最优Pareto 前沿中，全局最优解不存在唯一性。本文采用理想点法从84 组候选配合比中遴选出不同偏向的理论最优配合比参数。首先，对各组目标函数值进行向量规范化处理，得到规范化指标；其次，依据各优化目标的重要程度分配权值，强度偏向型、经济偏向型、 环保偏向型和均衡型4 种配比方案对应的权重向量W分别取(0.5，0.25，0.25)、(0.25，0.5，0.25)、(0.25，0.25，0.5)和(1/3，1/3，1/3)；再次，确定正理想解和负理想解；然后，分别计算各配比方案到正理想解和负理想解的距离；最后，计算各方案与正理想解的接近程度，选取接近度最高的一组配合比参数作为决策解。按照上述步骤，即可得到不同偏向的最优配比方案，如图4 和表7所示。由图4、表7 可知，方案A 的28 d 抗压强度较高，方案B 较为经济，方案C 在保证强度的情况下，还具有较好的环保性，方案D 整体较为均衡且处于较高水平。因此，获得的4 个不同偏向的最优配比方案均符合预期。

图4 Pareto 前沿散点分布

表7 不同偏向的理论最优配合比参数

4.4 理论最优配合比参数的验证将表7 中的最优配合比参数与用传统经验设计方法获得的配比方案（即初始方案，其配合比参数见表5）进行对比，通过分析各组分材料用量和3 个目标函数值来验证本文智能设计方法的优越性。表8 为两种设计方法得到的配合比优化结果的对比。从表8 可以看出：（1）优化方案A 较之初始方案具有更高的抗压强度和更低的单方造价，虽然碳排放量有所增加，但仍在可接受范围内；（2）优化方案B 与初始方案的抗压强度相当，碳排放量也较为接近，但其单方生产成本降低约8.51%；（3）在确保力学性能的前提下，优化方案C 的单方造价和碳排放量分别比初始方案下降了10.37%和4%；（4）优化方案D 与优化方案B 类似，在大幅降低单方造价的同时，保持抗压强度和碳排放量基本不变。总体而言，用本文智能设计方法得到的最优配比方案相比于传统经验设计方法的结果更加合理、经济、环保，从而证明了该方法对于HPC 配合比优化设计的有效性和可靠性。

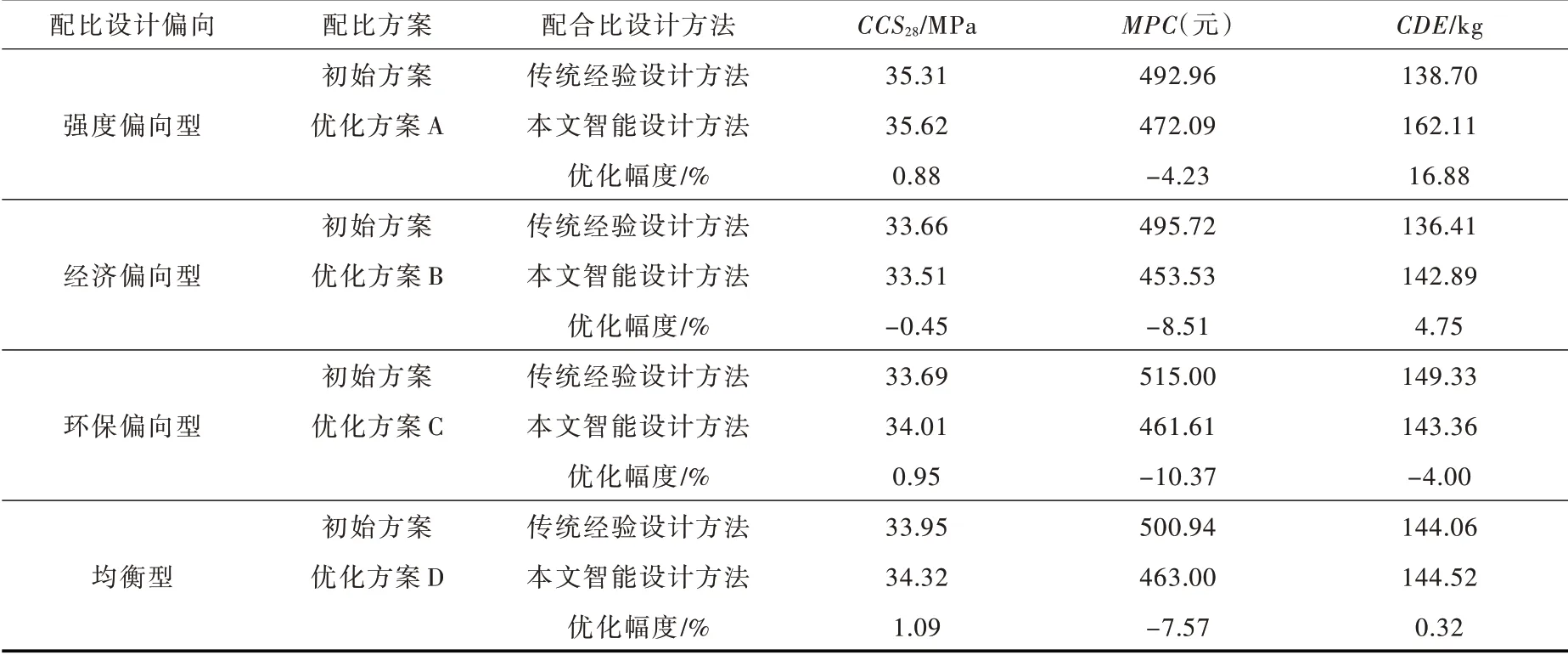
表8 本文智能设计方法与传统经验设计方法得到的配合比优化结果对比

5 结论

（1）针对性地提出了一种基于随机森林算法和AEPSO 的HPC 配合比优化设计新方法，避免了单目标、单参数优化方法的盲目性，充分考虑了不同目标之间的关联性，实现了多目标需求下的HPC 配合比智能化设计。（2）本文智能设计方法不仅可以实现对HPC 抗压强度的高精度预测，还可以通过联立约束条件求解出符合该条件下的理论最优配合比参数，大大减少了物理试验的工作量，提高了配合比优化设计的效率。（3）多目标联合优化数学模型能在一次求解后得到多个Pareto 最优解，这些解给配比设计人员提供了更多的选择空间，使其可以根据实际需求选取不同偏向的最优配比方案，具有较好的指导作用和应用价值。（4）将优化结果与初始方案进行对比，可以看出本文方法在一定程度上能节约资源、降低造价和减少污染，且不同偏向的最优配比方案对应的各项指标均能达到预期要求。（5）所提出的配合比智能设计方法除适用于高性能混凝土之外，还适用于常态混凝土、碾压混凝土等。尽管该方法取得了比传统经验设计方法更好的优化结果，但其在设计过程中难以考虑原材料的质量特性对混凝土性能指标的影响，后续将结合混合知识表征技术进一步提高所提方法的实用性。