SOTEM数据拟二维反演研究与应用

宋婉婷,陈卫营*

(1.中国科学院地质与地球物理研究所 中国科学院矿产资源研究重点实验室,北京 100029;2.中国科学院地球科学研究院,北京 100029;3.中国科学院大学 地球与行星科学学院,北京 100049)

0 引 言

电性源短偏移瞬变电磁法(Short-offset Transient Electromagnetics Method,SOTEM)利用接地导线源向地下发射激励电流，在0.3～2.0倍探测深度的偏移距范围内观测纯二次电磁场信号，并通过处理与解译观测信号达到探测地下目标体的目的。大量研究和应用表明，SOTEM具有探测深度大(一般可达2 km)、分辨率高、野外施工灵活等优点，在深部金属矿探测、煤田水文地质调查等领域表现出巨大潜力。

受数值模拟手段和计算机计算效率的限制，SOTEM数据的多维反演尚未完全实用化，目前还以一维反演为主。传统的一维反演方法是对一条测线上的测点逐一进行单点反演，反演结果只是利用层状大地模型简单的拼接来描述地下介质的电性信息。在实际测量中，不同测点通常会具有不同的地形和噪声环境，这种单点的反演方式通常会造成相邻测点反演结果不连续，产生虚假的局部异常，造成反演解释的困难。为了解决单点一维反演的电阻率横向突变问题，同时保留一维反演速度快的优势，Auken等探索出对反演模型或数据施加约束条件的拟二维反演方法，并成功应用于多种电磁数据的反演解释中。Auken等最早将横向约束用于直流电法数据的反演中，后又在最小二乘法二维反演中改进了约束矩阵，结果表明拟二维反演在提高分辨率和压制噪声方面都有所改善。Siemon等首次将横向约束反演技术应用于直升机载频域电磁数据中。Santos等提出了一种基于横向约束算法的直流电阻率和时域电磁数据的联合反演方法，并验证了该方法的实际应用价值。殷长春等将横向约束方法进一步改进，提出了加权横向约束(WLCI)思想，并应用于频率域航空电磁数据的拟二维反演中，后又将该方法用于时间域航空电磁拟二维反演。近期，基于OCCAM反演的光滑拟二维反演方法和基于量子行为粒子群算法的拟二维反演技术也应用于航空瞬变电磁数据的处理中。

在SOTEM勘探中，测线布置一般较长，测点多且密集，由同一发射源激发所得的数据稳定性较好。其尤其是在煤矿领域应用广泛，沉积煤系地层横向连续性好，同一测线上的电阻率和厚度在横向上变化一般不大。将约束思想用于SOTEM数据处理中能大大提高反演结果的纵、横向连续性，并且在一定程度上降低大深度探测中晚期信号易受干扰的影响。本文在前人研究基础上，实现SOTEM数据的拟二维反演，并通过对理论模型数据和实测数据的反演评估拟二维反演在SOTEM数据处理中的有效性，旨在提供一种可靠、稳定、实用的SOTEM数据反演方法。

1 SOTEM一维响应计算

SOTEM一维正演从水平电偶极子源出发，获得具有积分形式的接地长导线源的频率域响应，再通过傅氏变换转化为时间域的响应。置于地表的电偶极源在直角坐标系下可以产生三磁(、、)、三电(、、)共6个电磁场分量。已有研究表明水平电场分量和垂直磁场强度分量的场值分布、衰减更利于观测和处理。本文研究选用野外实际观测中最为常用的垂直磁场强度分量(或其时间导数d/d)。直角坐标系下，置于地表的水平电偶极值在层状大地表面产生的垂直磁场强度计算公式为

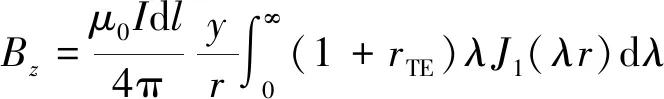
(1)

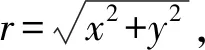
当大地磁导率等于自由空间中的磁导率时，反射系数表达式为

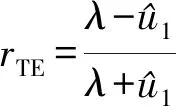
(2)

对于层大地，有递推公式为

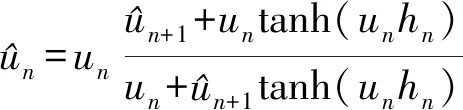
(3)

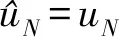
(4)

通过偶极子叠加得到有限长导线源的电磁场，其表达式为

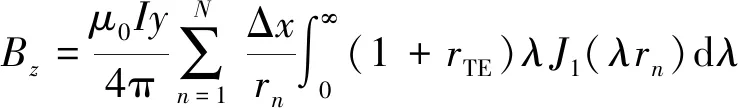
(5)

式中：为长导线源分割成的偶极子个数；Δ为每个偶极子的长度；为接收点到每个偶极子中心的距离。

2 拟二维反演方法

拟二维反演的主要思想是通过在相邻测点间施加约束条件(电阻率、厚度或深度)，以保证电阻率断面图的纵、横向连续性，其出发点仍为一维反演。基于正则化思想，一维反演的目标函数可归结为

()=()+()→min

(6)

式中：()为数据目标函数；()为模型先验信息目标函数；为正则化调节因子。

在一维正则化反演理论的基础上，引入模型横向粗糙度目标函数(())和纵向粗糙度目标函数(())，确定拟二维整体反演的目标函数。其表达式为

()=()+[()+()+()]

(7)

式中：、、分别为模型先验信息、模型横向粗糙度、模型纵向粗糙度的正则化系数。

整条测线各测点的大地模型参数按一列排布，=[,…,1,,,…,1,-1,…,,1,…,,,,1,…,,-1]，其中,为第个测点第层的电导率，,-1为第个测点第-1层的厚度。

观测数据的目标函数为

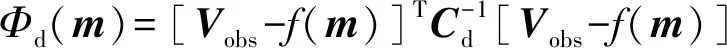
(8)

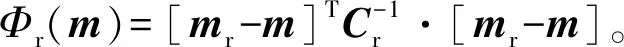
(9)

(10)

式中：Δ为相邻测点间距离；,为第个测点第层厚度。

在反演迭代过程中，通过线性搜索自适应迭代的方式自动确定，即在每次迭代过程中，通过线性搜索的方法，自动选取最优的正则化因子。、、在初始反演时根据实际情况选择合适取值，在反演过程中保持不变。

为求得目标函数的最优解，以第+1次迭代为例，令目标函数对待求模型参数+1的偏导等于0。其表达式为

(11)

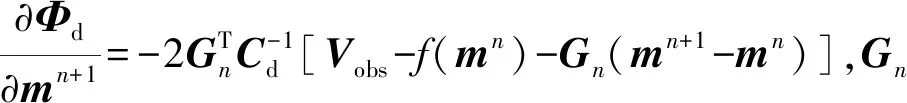
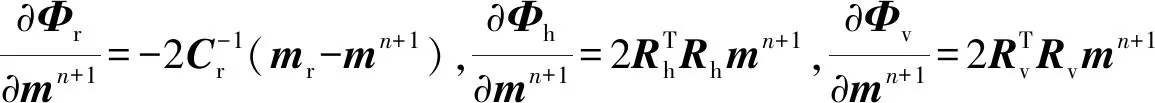
+1=

(12)

求解上述线性方程组，即可得到第+1次迭代所求得的新模型向量+1。反演的终止条件则为()≤1，其中为测线电磁数据个数。

3 理论模型拟二维反演

首先通过一个如图1所示的二维地电理论模型来验证拟二维反演处理SOTEM数据的效果。模型共分为3层：第一层厚度为200 m，电阻率()为200 Ω·m；第二层底界面起伏变换，厚度为200～400 m，电阻率()为50 Ω·m；第三层为基底，电阻率()为500 Ω·m。利用单点一维正演获得整条剖面的响应数据，正演中发射源长度为1 000 m，测线长度为1 000 m，点距为20 m，偏移距为500 m，发射电流为1 A，计算时间为0.1～100.0 ms，共分41个时间道，计算场量为垂直磁场强度分量。正演计算中收发布置如图2所示。

图1 理论模型示意图Fig.1 View of Theoretical Model

图2 一维正演收发布置图Fig.2 Layout of Transmitter and Receivers for 1D Forward

对正演获得的响应数据分别进行单点一维反演和拟二维反演。初始模型为100 Ω·m的均匀半空间，反演最大深度取1 100 m，首层厚度10 m，往下各层厚度以上一层1.1倍数递增，共包含30层，迭代次数设置为7次。拟二维反演中，正则化系数、、取值都设为1，正则化因子初始值设为1 000，在迭代过程中利用线性搜索算法自适应选取最优的正则化因子。首先对正演得到的无噪声数据进行反演，从而得到单点一维反演和拟二维反演电阻率-深度断面图(图3)。由图3(a)、(b)可以看出，当数据不含噪声时，一维反演与拟二维反演结果基本吻合，都很好地恢复了真实模型的电阻率分布，对层界面刻画也非常清晰。图3(c)给出了两种反演模式下整条测线的拟合残差曲线，可以看出两种反演的拟合残差都收敛到较低水平(最大值不超过3.6%)，且拟二维反演情况下拟合残差更小。

图3 无噪声反演结果Fig.3 Inversion Results Without Noise

为研究噪声水平对反演结果的影响，本文在所有测点的正演数据中按照时间道早晚依次添加不同程度的白噪声。第一组噪声水平为1%～50%，第二组为1%～100%。分别对两组加噪后的数据进行单点一维反演和拟二维反演，反演参数与前述无噪情况一致，获得整条剖面的电阻率-深度断面图(图4、5)。从图4、5可以看出，当反演数据含噪时，单点一维反演结果虽仍能反映出模型的大致电性分布，但受噪声影响，电性层分界面变得毛糙，横向连续性变差。特别是当噪声水平较高时，出现了相邻测点电阻率和层厚度的突变，空间连续性变差，产生了虚假的局部异常(图5)。而拟二维反演结果受噪声的影响相对较弱，仍能很好地反映模型的真实电性结构，对模型电性界面的刻画清晰且光滑，很大程度上降低了噪声引起的这种电阻率纵、横向突变，使得仅由个别测点引起的假异常现象得到很好的抑制。通过观察拟合残差可以发现，在相同的迭代次数情况下，拟二维反演并不一定能减小最终的拟合残差，且拟二维反演的拟合残差普遍大于单点一维反演结果。这是因为在拟二维反演中，反演模型受横向电阻率约束，并不能完全拟合曲线的实际形态。当个别测点的曲线出现严重畸变时，拟二维反演的拟合残差可能会很大，但会避免追求低拟合残差带来的错误结果。

图4 加入1%～50%白噪声的反演结果Fig.4 Inversion Results with 1%-50% White Noise

图5 加入1%～100%白噪声的反演结果Fig.5 Inversion Results with 1%-100% White Noise

同时，由于拟二维反演同时处理的是整条剖面的数据，当总迭代次数相同(7次)时，相较于单点一维反演，拟二维反演需要进行的正演计算和雅克比矩阵求解次数更少，从而反演所需时间更少，效率更高。表1给出了上述3种噪声水平下，采用单点一维反演和拟二维反演处理整条剖面数据的耗时。计算环境为：Intel(R)Xeon(R)CPU E5-1603 v4@ 2.80 GHz处理器，16 GB内存。由表1可知，拟二维反演可显著提升数据反演的效率。

表1 单点一维反演与拟二维反演耗时Table 1 Time Consuming of Single-site 1D Inversion and Quasi-2D Inversion

最后，本文测试了拟二维反演对复杂模型的反演效果。设计如图6所示的一个双异常体模型。对该模型进行一维正演获得垂直感应电动势d/d响应，并对数据添加和图5一样的高水平噪声。对含噪数据分别进行单点一维反演和拟二维反演，反演参数与前述一致，结果如图7所示。从图7可以看出，对于含两个异常体的复杂模型，当噪声水平较高时，采用单点一维反演很难清晰地反演出两个异常体的形态，反演结果出现了大量的假异常[图7(a)]；而当采用拟二维反演时，虽然也存在个别的假异常，但目标异常体的横向范围得到了很好的恢复[图7(b)]；从拟合残差曲线来看，拟二维反演的拟合残差在200～400号点之间存在一个高值区域[图7(c)]，这是因为该范围内的响应畸变较严重，在横向约束下反演迭代中程序未完全按照原始数据的形态进行拟合。

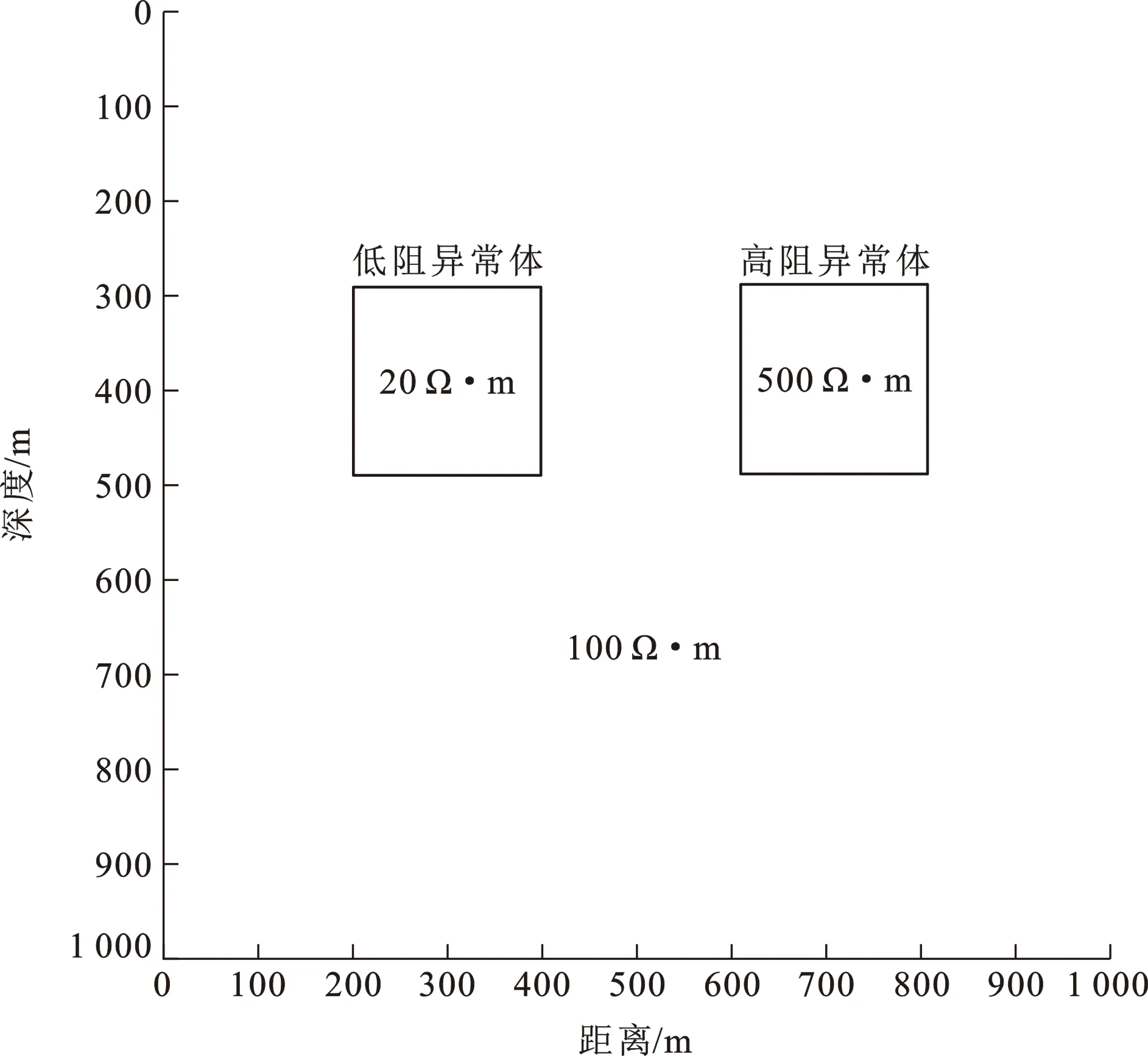
图6 双异常体复杂模型示意图Fig.6 View of Complex Model with Two Anomaly Bodies

图7 含噪复杂模型反演结果Fig.7 Inversion Results of Complex Model with Noise

4 实测数据拟二维反演

为进一步验证拟二维约束反演在处理SOTEM数据中的有效性和优越性，本文对山西晋城地区某煤矿的实测SOTEM数据进行反演处理。测区位于沁水煤田高平矿区，探测目的是调查3#煤富水采空区分布和区内富水导水通道，并评价奥陶系灰岩地层含水性。测区主要地层及电性特征如表2所示。

表2 测区地层综合电性特征Table 2 Comprehensive Electrical Properties of Strata in the Survey Area

本次SOTEM探测工作共布置测线42条，编号为L1～L42，测线方向为EW向，测线间距为50 m，测点间距为20 m。本文以其中两条测线L4和L18为例，分析拟二维反演效果。发射源与测线布置及相关几何参数如图8所示，发射电流为12 A，基频为12.5 Hz，观测垂直感应电压()分量，接收线圈有效面积为100 m。观测仪器为加拿大凤凰公司的V8多功能电法工作站，测点干扰较小且数据较为光滑时，单点观测时间为2 min，测点电磁干扰较大时，观测时间为5 min。实测数据质量整体尚好，但由于L4测线靠近村庄，受附近民用电线及居民电器影响，数据质量相对较差，大部分测点的晚期信号信噪比较低，个别测点甚至在全时间段内出现严重畸变。两条测线的实测多测道感应电压曲线如图9所示。本文在进行反演处理时，对晚期畸变严重的时间道数据进行了剔除。

图8 测线及发射源布置图Fig.8 Layout of Survey Line and Emission Source

图9 实测感应电压多测道曲线Fig.9 Measured Multichannel Curves of Induced Voltage

利用SOTEM单点一维反演和拟二维反演技术对经预处理后的每条测线数据进行反演。初始模型为100 Ω·m的均匀半空间，反演最大深度为600 m，首层厚度为10 m，以下各层厚度按上层厚度的1.05倍增加，共分为29个电性层，拟合次数设置为10次。拟二维反演中，先验信息采用一维等效源反演结果，正则化系数、、取值为1、10、1，正则化因子初始值设为1 000。图10和图11为得到的高程-电阻率断面图。由图10、11可以看出，对于每条测线，单点一维反演和拟二维反演结果对地层电性结构的反映在整体上基本一致。尤其是对于浅部地层，两种反演方法对电性结构变化细节的反映也能很好的吻合。但是随着深度的增大，电磁信号分辨率降低，单点一维反演的不确定性导致其个别测点的结果在横向上出现较明显的不连续性。特别是当原始数据受到干扰程度较高时，深部电阻率横向突变现象尤为严重。L4测线60、160和260 m处出现纵向延伸的局部低阻带[图10(a)]，L18测线0～350 m范围内也出现多处这种“挂面条”式低阻带[图11(a)]，这些异常现象都有悖于煤矿区域地下结构横向连续性高的特点，给解释带来困难。而经过横向约束的拟二维反演结果展现了更接近真实情况的地下电性结构，在很大程度上降低了这种电阻率横向上的突变，使得仅由个别测点引起的假异常现象得到很好的抑制[图10(b)、11(b)]。为了验证反演结果的可靠性，本文将矿方在L18测线320号点附近实施的一个钻孔(ZK-206)结果绘制于图11中。根据钻孔揭示，该位置在钻进深度245 m范围内未发现采空区。煤系地层深度范围内地层应呈高阻反映，这与拟二维反演结果更为接近。另外，根据L18测线反演结果推断的两条断层(图11中F1和F2断层)与真实断层的位置基本一致，进一步验证了反演结果的可靠性。

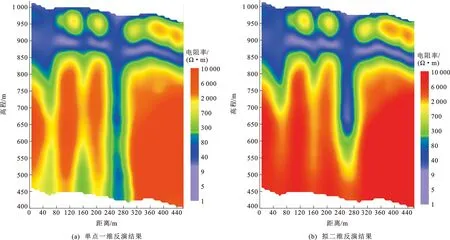
图10 L4测线反演结果Fig.10 Inversion Results of Line L4

图11 L18测线反演结果Fig.11 Inversion Results of Line L18

5 结 语

本文针对SOTEM的特点和需求，研究了SOTEM数据拟二维约束反演，采用自适应正则化算法，在单点一维反演的基础上引入模型粗糙度目标函数，对相邻测点之间模型参数进行横向及纵向约束。通过对理论模型数据和野外实测数据的处理，验证了该方法可克服单点一维反演结果中电阻率横向连续性差的问题，有效压制噪声对反演结果的影响，大大提高了反演精度，且计算效率更高。