基于随机森林的陕西省西安市近地表气温估算

冯 瑞，杨丽萍，侯成磊，王 彤，张 静，肖 舜

(1.长安大学 地球科学与资源学院，陕西 西安 710054;2.长安大学 地质工程与测绘学院，陕西 西安 710054;3.山东农业工程学院 国土资源与测绘工程学院，山东 济南 250100;4.陕西师范大学 地理科学与旅游学院，陕西 西安 710119)

0 引 言

近地表气温指距离地面1.5～2.0 m的大气温度。作为描述地表大气环境的重要指标，近地表气温是气象观测的基本要素之一，也是地表与大气能量交换、水循环及生态过程研究的重要输入因子。近地表气温与人类的日常生活和社会生产活动息息相关，高精度、大范围近地表气温监测对于生态环境、农业生产、气候变化等研究具有重要的现实意义。

气象站点观测数据是获取近地表气温的直接途径，具有准确性高等特点。早有学者基于气象观测数据，利用反距离权重、样条函数和克里金插值等多种空间插值法获取了具有空间连续性的气温数据。然而受多种因素限制，通常情况下气象站点数量有限，在站点稀疏和分布不均匀的地区，利用空间插值法得到的气温数据误差较大。相较于传统的观测方法，卫星遥感技术具有大范围、实时性和经济性等优势，同时可提供比气象站点观测资料更完整的空间异质度信息。随着卫星遥感技术不断发展，国内外学者基于遥感数据在近地表气温反演中开展了大量研究，提出了多种近地表气温反演算法，主要可概括为以下4类。第一类为常规统计法，包括单因子统计法和多因子统计法。该方法通常基于地表温度(Land Surface Temperature,LST)与实际观测气温数据间的相关关系进行气温模拟。陈命男利用一元线性回归方法分别对上海市2007年和2008年的地表温度与气温观测数据进行拟合，判定系数()分别为0.566 0和0.706 6；Lin等在结合归一化植被指数(Normalized Difference Vegetation Index,NDVI)和环境绝对湿度等因子估算复杂地形山区气温时发现，判定系数从0.60～0.65增加到0.71～0.88，这表明在解释复杂地形表面能量通量的时空变化时必须考虑相关的环境因素；Mohammadi等利用地理加权回归方法比较了单变量和多变量模型反演大气温度的精度，发现采用多变量回归方法精度更高，均方根误差(Root Mean Square Error,RMSE)为0.62 ℃，平均相关系数为0.99。第二类为温度植被指数(Temperature-Vegetation Index,TVX)法。该方法是一种利用地表温度和光谱植被指数间的负相关性，从遥感数据中提取气温的空间邻域运算方法，适用于浓密植被覆盖地区。徐永明等通过去除温度植被指数空间窗口内残余水体和云像元改进温度植被指数法，提高了算法适用范围。第三类为能量平衡法。Pape等基于能量平衡方程，并结合下垫面植被及地貌数据反演近地表气温，均方根误差为0.37 ℃～1.02 ℃。第四类为机器学习法。Yoo等设计了8种不同变量输入方案，利用随机森林算法模型研究了洛杉矶市和首尔市的日最高气温和最低气温，最佳模型判定系数大于0.7，均方根误差小于1.7 ℃；高亮等采用随机森林、支持向量机、AdaBoost和岭回归等4种机器学习模型拟合观测气温与影响要素的相关关系，结果表明随机森林模型精度最高，判定系数平均值为0.85，均方根误差平均值为0.50 ℃；邢立亭等使用随机森林模型估算了兰州市近地表最高气温和最低气温，模型估算效果良好，判定系数分别为0.921和0.916。

综上所述，前人已提出了多种近地表气温遥感反演方法，并在近地表气温监测中取得了显著成效。其中，因考虑了多种环境因子，多因子统计法的反演精度通常高于单因子统计法；温度植被指数法输入参数少且相对简单，但对于低植被及裸土地区，该方法并不适用；能量平衡法具有深厚的物理基础，但计算过程相对繁杂；机器学习法已广泛应用于各个领域，已有学者利用机器学习法在近地表气温反演中进行了有益尝试，大量研究表明随机森林模型在获取高时空分辨率近地表气温中精度较高，表现良好。气温的时空分布与变化受海拔高度、地形、下垫面性质和纬度等多种因素的综合影响，且影响关系复杂。传统的统计回归模型对这一复杂耦合关系的表达能力有限；随机森林模型训练速度快，模型参数调整相对简单，可以较好地拟合因变量与多个自变量的非线性关系，为探讨这一复杂耦合关系提供了新的途径。

陕西省西安市是中国西部地区的中心城市。近年来，随着西安市向国际化大都市的快速迈进，城市化进程飞速发展，人口激增，城市规模不断扩张，人工景观大幅代替自然景观。人类密集活动以及城市下垫面性质的变化加剧了西安市局地气候与环境问题。前人研究表明，西安市平均气温呈上升趋势，且市区气温上升速率高于郊县区。以城市热岛效应为典型的城市气候与热环境问题愈演愈烈，这一问题不仅可以通过热危害直接威胁人体健康，还会加重空气污染，间接增加呼吸系统和心脑血管等疾病的发病率。在上述背景下，开展西安市近地表气温估算研究，以期为改善城市气候、减缓城市热岛效应、打造适宜人居环境提供参考。

本文首先基于西安市Landsat 8卫星数据提取地表温度、归一化植被指数、归一化建筑指数(Normalized Difference Built-up Index,NDBI)、改进的归一化水体指数(Modified Normalized Difference Water Index,MNDWI)和地表反照率(Albedo)等5种遥感因子，基于30 m空间分辨率的SRTM DEM数据提取高程(Altitude)、坡向(Aspect)和坡度(Slope)等3种地形因子，将提取的8个参数进行相关性和重要性综合分析；然后在此基础上进行不同参数组合，构建多个估算气温的随机森林模型；最后基于气象站点观测数据，利用交叉验证的方法评估模型性能、验证模型精度，并选取最优参数组合方案进行近地表气温估算。

1 研究区概况及数据来源

1.1 研究区概况

西安市地处陕西省关中平原中部，经度范围为107.40°E～109.49°E，纬度范围为33.42°N～34.45°N(图1)。西安市整体呈南高北低、阶梯状的地势特点，城市以北的渭河平原和南部的秦岭山地形成强烈的地貌对照。西安市管辖11个区和2个县，其中灞桥区、未央区、新城区、莲湖区、雁塔区、碑林区为西安市中心城区。长安区、临潼区、高陵区、阎良区、鄠邑区、蓝田县和周至县是西安市的周边郊县区。山区主要指东西向横跨周至县、鄠邑区、长安区和蓝田县的秦岭山区。西安市属暖温带半湿润大陆性季风气候，四季分明，年平均气温为13.0 ℃～13.7 ℃，年降水量为522.4～719.5 mm。

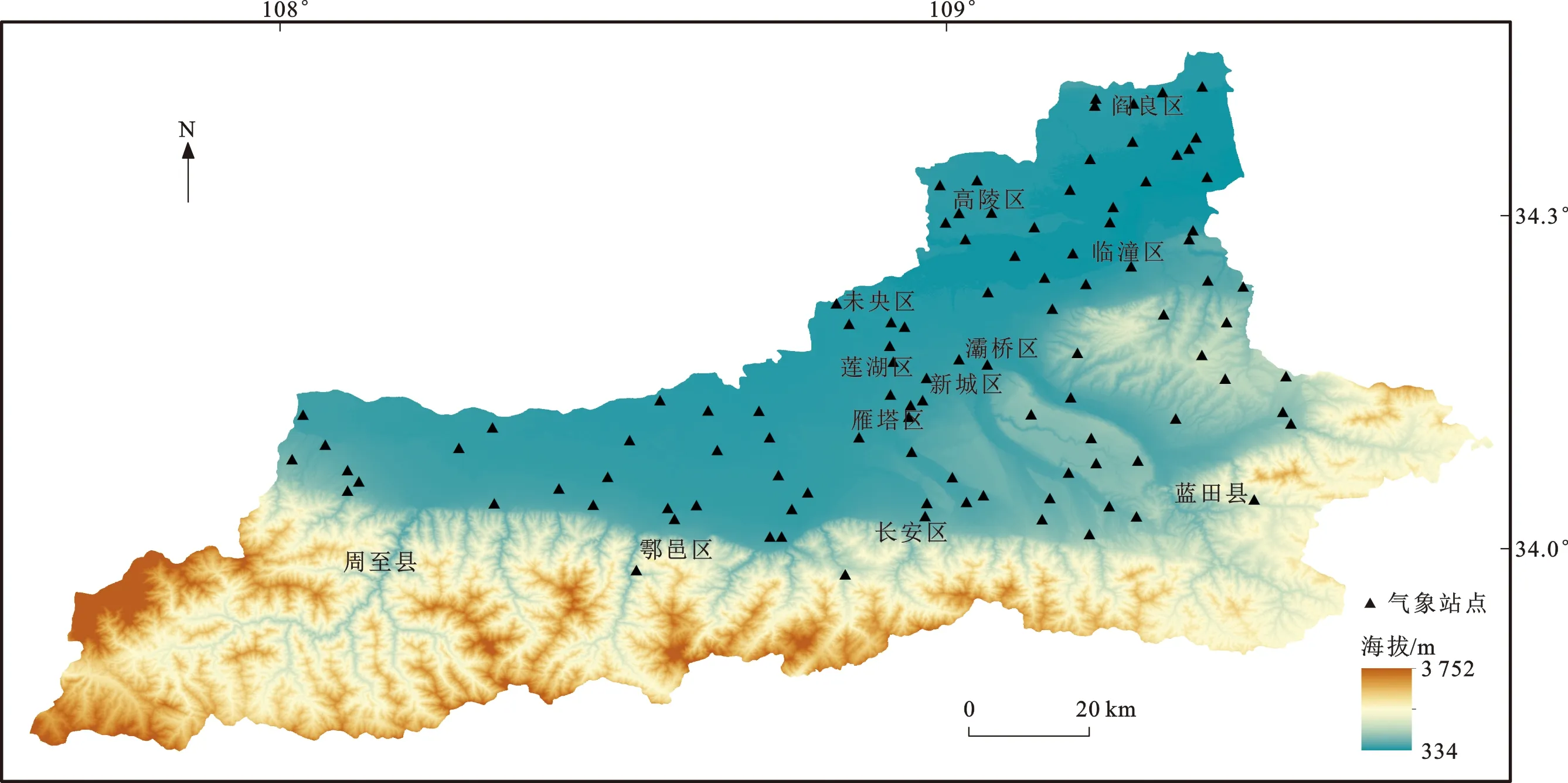
图1 陕西省西安市地区气象站点分布Fig.1 Distribution of Meteorological Stations in Xi’an City of Shaanxi Province

1.2 数据来源

遥感数据采用2016年5月16日的Landsat 8卫星影像，数据来源于地理空间数据云(http:∥www.gscloud.cn/)。利用ENVI5.3软件对卫星影像进行了辐射定标、大气校正及拼接与裁剪。以30 m空间分辨率的SRTM DEM作为高程数据，数据来源于美国地质调查局(http:∥www.usgs.gov/)，将6幅DEM数据进行拼接、裁剪得到覆盖全研究区的DEM数据。

气象数据为2016年5月16日西安市地面自动气象站点逐小时气象观测数据，采用与卫星过境时间相一致的观测数据进行模型性能评估与精度验证。研究区共102个气象站点，由于卫星过境时不是整点时刻，所以取过境时相邻整点实测气温数据进行线性插值计算出卫星过境时的气温。研究区气象站点分布如图1所示。

2 研究方法

2.1 自变量获取

2.1.1 地表温度

本文采用胡德勇等针对Landsat 8第10波段(TIRS 10)提出的地表温度单窗算法(简称为TIRS 10-SC算法)计算地表温度。胡德勇等利用TI-RS 10-SC算法、覃志豪单窗算法和Jiménez-Muňoz算法反演了不同植被覆盖类型的地表温度，认为TIRS 10-SC算法可以较好地应用于Landsat 8卫星影像数据地表温度反演。TIRS 10-SC算法公式为

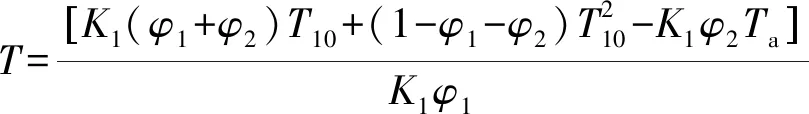
(1)

=

(2)

=(1-)·[1+(1-)]

(3)

式中：为地表温度；为TIRS 10的亮温；为大气平均作用温度；为TIRS 10地表比辐射率；为TIRS 10大气透射率；取常数1 321.08 K；和为中间参量。

2.1.2 其他自变量

影响近地表气温的因素众多，除地表温度外，太阳辐射、植被、水体、建筑物分布及地形等因素均具有一定影响。因此，本文引入其他遥感因子(包括归一化植被指数、归一化建筑指数、改进的归一化水体指数和地表反照率)以及地形因子(包括高程、坡向和坡度)作为构建随机森林气温估算模型的输入参数。遥感因子基于Landsat 8卫星数据获取，计算公式见表1，地形因子由DEM数据获取。

表1 遥感因子提取算法Table 1 Extraction Algorithms for Remote Sensing Factors

2.2 随机森林

随机森林是Breiman提出的一种基于决策树组合的可用于分类、回归以及多维数据处理的机器学习算法。较传统决策树算法而言，该算法能够平衡分布不均匀样本的误差，分类精度高，对异常值和噪声有很好的容忍度。随机森林是未经修剪的分类树或回归树的集合，这些树是通过训练数据的自举样本和树归纳中的随机特征选择而创建的，随机森林选取总样本数的2/3作为训练集构建决策树，剩余1/3数据用于验证所构建的模型性能。通常可通过调整决策树的数量以及单棵决策树的特征数量来提高随机森林模型的性能，本文使用循环迭代法进行参数优化。对于决策树数量设置，将决策树数量步长设置为10，自第10棵树起每加入10棵树模型运行1次，决策树数量至300棵时模型结束，将判定系数最大值对应的模型作为此次运算的最佳结果保存。对于单棵决策树数量的设置，在1到模型输入参数数量之间选择一个合适的值作为单棵决策树的特征数量，通过在决策树棵树的循环下嵌套一个循环体，将步长设置为1，把表现最好的作为单棵决策树的特征数量进行保存。本文随机森林模型的构建通过MATLAB软件中的Random Forest工具箱完成，模型实现步骤如下。

步骤一：通过自举采样方法Bootstrap从原始数据集中随机抽取次(有放回)，样本集组成个训练集，未被抽到的数据为袋外(Out of Bag,OOB)数据，可用于评估构建模型的性能。

步骤二：新构建的每个训练集均单独作为一棵决策树，每棵决策树在生长过程中均不进行剪枝。

步骤三：重复步骤二次，将生成的棵决策树组成随机森林，并应用于分类和回归。对于每棵树都能得到一个袋外数据误差统计，对所有决策树的袋外数据误差取平均后可得到随机森林泛化误差估计，袋外数据误差是无偏估计。

2.3 变量重要性计算

随机森林可以在训练过程中生成输入变量的重要性度量。本文随机森林中的变量重要性利用平均精度下降(Mean Decrease Accuracy,MDA)进行表征，该方法是基于袋外数据误差的一种重要性评判方法。其基本原理是在外包样本数据集中改变某一输入参数值，然后计算造成的估算误差，通过得到的误差评判参数的重要性。若误差较大，说明该变量对预测结果越敏感，同时重要性值越大，对模型的贡献越高。

2.4 模型验证方法

随机森林是随机选取样本数据的过程，其本身具有交叉验证的优势，当模型中决策树的数目足够保证每个样本都可以充当一次训练集和样本集时，可以最大程度地避免模型过度拟合，同时提升模型的外推能力。K折交叉验证是对交叉验证的进一步发展和推广，根据Kohavi的研究结果，10倍的变异系数在估计模型预测误差时效果最佳，因此，本文采用10折交叉验证来评估模型性能，采用判定系数和均方根误差作为模型性能的评价指标。

3 结果分析

3.1 变量相关性与重要性分析

3.1.1 相关性分析

为定量分析自变量与近地表气温之间的关系，本文选用Pearson相关系数对近地表气温和8个输入参数之间的潜在关系进行研究，结果如图2所示。

**表示在0.01水平(双侧)上显著相关；*表示在0.05水平(双侧)上显著相关。纵坐标中，1表示地表温度；2表示改进的归一化水体指数；3表示归一化建筑指数；4表示归一化植被指数；5表示地表反照率；6表示高程；7表示坡向；8表示坡度图2 相关性分析结果Fig.2 Correlation Analysis Results

相关性涉及的8个自变量包括5个遥感因子和3个地形因子。遥感因子中，地表温度、改进的归一化水体指数和归一化植被指数通过了显著性检验，归一化建筑指数和地表反照率未通过显著性检验。其中，地表温度相关性最高，相关系数为0.551；地表反照率相关性最低，相关系数为0.041。地形因子中，高程和坡度通过显著性检验，坡向未通过显著性检验。高程相关性最高，相关系数为-0.803；坡向相关性最低，相关系数仅0.021。整体来看，8个自变量的相关性从高到低依次为高程、地表温度、坡度、改进的归一化水体指数、归一化植被指数、归一化建筑指数、地表反照率、坡向。其中，地表温度、改进的归一化水体指数、归一化建筑指数、地表反照率和坡向与近地表气温成正相关关系；归一化植被指数、高程和坡度与近地表气温成负相关关系；与近地表气温相关性最高的参数为高程，相关性最低的为坡向。

3.1.2 重要性分析

输入因子重要性评分用平均精度下降表示，结果如图3所示。由图3可见：在遥感因子中，地表温度对于近地表气温估算的重要性高于其他4个因子，地表温度的重要性评分最高，所对应的平均值也最高；归一化建筑指数重要性评分与平均值最低；改进的归一化水体指数、归一化植被指数和地表反照率的重要性评分以及平均值差别不大，表明这3个变量对于近地表气温估算的贡献度相当。在地形因子中，高程对于近地表气温估算的重要性评分最高，坡度次之，坡向最低，其对应的平均值亦然。整体来看，8个自变量中，高程的重要性评分及平均值最高，地表温度次之，其他6个自变量的重要性评分没有明显差异，归一化建筑指数重要性评分及平均值最低。从重要性分析来看，对近地表气温估算贡献度最大的是高程，其次是地表温度。

横坐标中，1表示地表温度；2表示改进的归一化水体指数；3表示归一化建筑指数；4表示归一化植被指数；5表示地表反照率；6表示高程；7表示坡向；8表示坡度图3 重要性分析结果Fig.3 Importance Analysis Results

3.1.3 相关性与重要性综合分析

第3.1.1和3.1.2节分别通过自变量与实测气温的相关性和重要性分析了影响因子对近地表气温估算的贡献度以及相关性和重要性表征变量不同的特征意义。这两种评价指标具有不同的量纲，为了综合考虑自变量的相关性和重要性，并消除不同指标之间的量纲影响，对相关系数和重要性评分进行归一化(MIN-MAX Normalization)处理，将数据结果映射到[0,1]，为判定自变量的贡献度大小及设计不同模型参数组合方案奠定基础。

横坐标中，1表示地表温度；2表示改进的归一化水体指数；3表示归一化建筑指数；4表示归一化植被指数；5表示地表反照率；6表示高程；7表示坡向；8表示坡度图4 归一化综合评价结果Fig.4 Normalized Comprehensive Assessment Results

归一化处理结果如图4所示。由图4可见：在遥感因子中，地表温度归一化结果最高，这与地表温度和近地表气温的相关性和重要性较高相一致，其次为改进的归一化水体指数，归一化结果最低的参数是地表反照率，表明遥感因子中对近地表气温估算贡献度最大的是地表温度；在地形因子中，高程的归一化结果最高，这与地形因子高程和近地表气温的相关性和重要性最高相一致，其次为坡度，最低为坡向，表明高程对估算近地表气温贡献度最大。整体来看，在构建随机森林模型估算近地表气温的过程中，8个自变量的贡献度从大到小依次为高程、地表温度、坡度、改进的归一化水体指数、归一化植被指数、归一化建筑指数、地表反照率、坡向，表明在近地表气温估算过程中地表温度和高程是最为重要的两个输入参数。近地表气温变化受多因素影响，一般情况下，在对流层中其垂直分布随高程的增加而降低，主要是由于距离地表越远，吸收的地面长波辐射越少，气温越低。地表吸收太阳辐射而增温，然后向外发出长波辐射，近地表气温因吸收地面辐射而增温，地表热量对近地表气温变化起直接的、主导的作用，因此，地表温度与近地表气温相关性较高。归一化植被指数反映植被覆盖度状况，植被覆盖度的变化会改变地表潜热、感热通量以及植被自身的蒸腾作用，进而对近地表气温变化产生影响，在近地表气温估算时考虑地表热量、水体、建筑等下垫面状况是非常有必要的。因此，根据归一化综合评价结果所反映的影响因子对近地表气温的贡献度大小，构建P2～P8(其中数字代表参数个数)共7种参数组合方案(表2)。

表2 模型参数组合方案Table 2 Combination Schemes of Model Parameter

3.2 随机森林近地表气温估算模型对比与性能评估

将第3.1.3节构建的7种参数组合方案分别输入随机森林模型进行近地表气温估算，采用10折交叉验证评估模型性能，结果如表3所示。由表3可知：7种参数组合方案下的随机森林模型训练集判定系数均高于0.916，均方根误差均低于0.467 ℃；所有模型验证集判定系数均高于0.726，均方根误差均低于0.840 ℃；训练集判定系数均高于验证集，均方根误差均低于验证集。7种参数组合方案分别构建的随机森林模型均能够对训练集和验证集进行较好的拟合，表明随机森林在研究区近地表气温估算中具有较好效果。

表3 随机森林模型性能Table 3 Model Performance of Random Forest

进一步分析发现，对于训练集，P5～P8方案模型判定系数大于P2～P4方案模型，且其均方根误差小于P2～P4方案模型，随着输入参数的增加，P5～P8方案模型判定系数和均方根误差无明显变化，模型性能较P2～P4方案模型表现较好且趋于稳定。对于验证集，P2～P5方案模型判定系数随着参数的增加而增加，均方根误差随着参数的增加而减小，P5方案模型性能表现较好；相比P2～P5方案模型，P6～P8方案模型判定系数出现先减后增变化，均方根误差出现先增后减变化。综合训练集和验证集来看，当全部参数输入模型后，随机森林模型(P8方案模型)性能表现最佳，其验证集精度优于P5方案模型，P8方案模型的训练集判定系数为0.934，均方根误差为0.425 ℃(P5方案模型训练集判定系数为0.935，均方根误差为0.426 ℃)，验证集判定系数为0.795，均方根误差为0.783 ℃(P5方案模型验证集判定系数为0.788，均方根误差为0.785 ℃)。因此，本文基于P8方案建立研究区随机森林近地表气温估算模型。

3.3 结果验证

从上述随机森林模型估算近地表气温的训练集及验证集结果来看，随机森林近地表气温估算模型精度较高，其中P8方案模型精度最高。为进一步验证模型精度，对基于最佳模型的近地表气温估算值与站点观测值进行线性拟合，结果如图5所示。由图5可见，近地表气温估算值与站点观测值的判定系数为0.792，均方根误差为1.055 ℃，气温估算精度较好。根据样本点相对1∶1线的分布情况可知，部分近地表气温估算值出现高值低估的现象。这一方面可能是由于近地表气温观测站点几乎全部分布在秦岭以北地区，研究区南部气温观测站点较为有限(图1)，所以观测气温的高值较多，在模型估算近地表气温过程中出现了一定程度的过拟合；另一方面，在气温估算过程中，未能考虑太阳辐射对地表温度直接作用的影响，从而也会导致近地表气温高值低估的情况。综上所述，虽然出现部分高值低估的现象，但根据总体估算精度来看，低估偏差在合理范围内，所构建的随机森林模型适用于西安市近地表气温的估算。

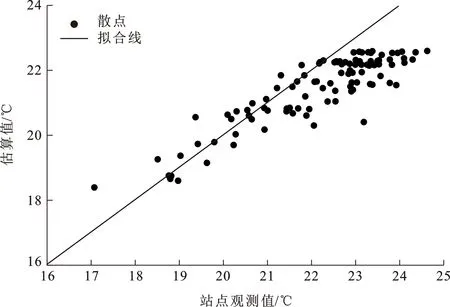
图5 近地表气温估算值和站点观测值散点图Fig.5 Scatter Plot of Estimated Temperature and Site Temperature

3.4 西安市近地表气温估算与空间分布特征

基于上述最佳随机森林模型，模拟得到 2016年5月16日西安市近地表气温(图6)。由图6可见，西安市近地表气温呈现显著的空间差异性，整体呈南低北高、中心城区高于郊县区的态势。

图6 2016年5月16日西安市近地表气温空间分布模拟图Fig.6 Spatial Distribution Simulation Map of the Near-surface Air Temperature in Xi’an City on May 16,2016

为进一步分析近地表气温的空间差异性，提取了不同区县的最低气温、最高气温、平均气温和平均高程，结果如表4所示。由表4可见，西安市13个区县的最低气温平均值为20.50 ℃，最高气温平均值为23.49 ℃，并且各区县最高气温均高于23.00 ℃，西安市平均气温为21.98 ℃。中心城区的3个气温指标均大于郊县区，其最低气温平均值、最高气温平均值以及气温平均值分别高于郊县区1.54 ℃、0.01 ℃和1.76 ℃。13个区县平均高程为380～1 433 m，从平均高程来看，秦岭山区横跨的周至县、鄠邑区、长安区和蓝田县的平均高程远高于其他辖区，这是引起这4个区县平均气温普遍低于其他辖区的一个重要原因，对于高程相近的其他辖区，近地表气温仍表现出空间差异性。伴随着城市化发展，地表下垫面类型发生改变，尤其对于中心城区，高层建筑、道路铺装等均会使植被、土地和水域等自然表面变为不透水面，进而改变了地表长波辐射能量，导致气温发生变化，这是城市气温产生空间差异的另一原因。此外，近地表气温受植被覆盖度、水域面积、人口密度及社会生产活动等众多因素影响，与中心城区相比，郊县区发展较慢且区域面积大，人类社会生产活动相对较少，使郊县区平均气温普遍低于中心城区。

表4 气温-高程分区统计Table 4 Statistics of Air Temperature-altitude in Different Districts

在中心城区内，灞桥区具有最低气温(19.20 ℃)，远低于其他5个辖区，差值为1.53 ℃～3.11 ℃；灞桥区平均气温为22.19 ℃，低于除雁塔区以外的其他4个辖区，差值为0.62 ℃～1.00 ℃。灞桥区内灞河、浐河和渭河交汇处，水域面积广，植被覆盖度相对较高，因此，灞桥区平均气温较低。雁塔区大型景观公园较多，绿化率高，平均气温最低。莲湖区、新城区和碑林区属于老城区，建筑密集，人口密度大，平均气温相对较高。对于郊县区，在周至县、鄠邑区、长安区和蓝田县均观测到最低气温(19.05 ℃)，明显低于高陵区和阎良区，与临潼区相差无异；其平均气温也明显低于高陵区和阎良区。秦岭位于西安市南部，东西向横跨周至县、鄠邑区、长安区和蓝田县，秦岭山区海拔高、植被覆盖度大，且以自然地表为主，因此，这4个区县平均气温低于高陵区、阎良区和临潼区。

综合图6和表4可知：西安市高温聚集在中心城区，最高气温为23.51 ℃；郊县区以及植被较为浓密的地区气温低于中心城区；低温聚集在秦岭山区，最低气温为19.05 ℃。西安市近地表气温呈现出中心城区较高、郊县区适中、山区较低的总体分布格局，且从中心城区到郊县区逐渐降低，山区气温普遍低于中心城区，呈现显著的城市热岛效应。

4 结 语

(1)相关性及重要性综合分析表明，在地表温度、归一化植被指数、归一化建筑指数、改进的归一化水体指数和地表反照率等5个遥感因子以及高程、坡向和坡度等3个地形因子中，高程对随机森林模型估算近地表气温的贡献度最大，其次是地表温度，坡向贡献度最低。

(2)7种参数组合方案构建的随机森林模型均能够对训练集和验证集进行较好的拟合，训练集判定系数均高于0.916，均方根误差均低于0.467 ℃，验证集判定系数均高于0.726，均方根误差均低于0.840 ℃；训练集判定系数均高于验证集，均方根误差均低于验证集。P8方案模型表现最优，其训练集判定系数为0.934，均方根误差为0.425 ℃，验证集判定系数为0.795，均方根误差为0.783 ℃，近地表气温估算精度判定系数为0.792，均方根误差为1.055 ℃，表明随机森林模型在研究区近地表气温估算中效果良好。

(3)2016年5月16日，西安市平均气温为21.98 ℃，13个区县的最低气温平均值为20.50 ℃，最高气温平均值为23.49 ℃。中心城区的3个气温指标值均高于郊县区，其最低气温平均值、最高气温平均值及气温平均值分别高于郊县区1.54 ℃、0.01 ℃和1.76 ℃。水域和植被覆盖度高的地区气温相对较低。中心城区内，灞桥区气温低于其他辖区；郊县区内，周至县、鄠邑区、长安区和蓝田县低于高陵区、阎良区和临潼区。西安市近地表气温南低北高，空间差异明显，自中心城区至郊县区到南部山区逐渐降低，呈现出显著的城市热岛效应。

(4)本文在近地表气温随机森林建模中综合考虑了地表温度、植被、水体、建筑物及地形等多种因素的影响，结合最优参数组合方案获取了精度较好的连续性空间近地表气温信息，对于开拓研究思路、提高估算精度、探索近地表气温遥感反演的新方法具有一定的参考意义，可为城市热岛效应研究提供新的思路。但是，影响近地表气温的因素众多，本文在模型设计时仅考虑了5个遥感因子和3个地形因子，未考虑太阳辐射、相对湿度、人口密度等自然因子及社会经济因子，后期将在模型中加入更多因子，深入探讨各因子对近地表气温估算的影响机理。此外，由于近地表气温实测气象站点数据有限，本文仅对单一时相数据进行了研究，下一步可在获取时间序列气温数据后开展近地表气温时空变化过程及机制研究，为城市生态环境保护和区域气候改善提供基础数据。