关注反思性学习，促进思维发展

李高洁

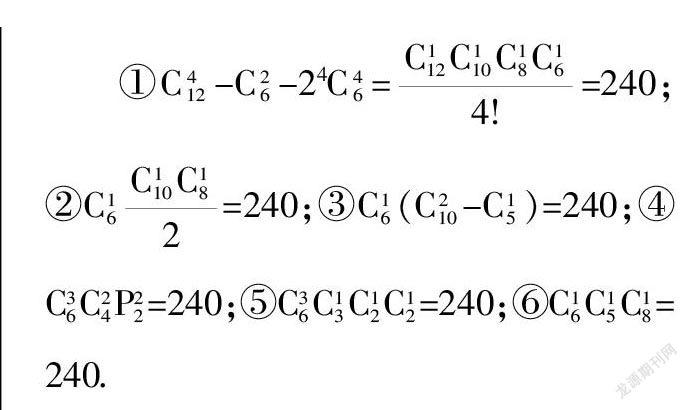
[摘  要] 在新课标的引领下，反思性学习的理念被提到高中数学教学的重要位置. 它对学生的元认知与思维能力的发展具有重要作用. 文章以它的理论基础为出发点，提出关注反思性学习，促进学生思维发展的具体措施有：审题反思，缜密思维;解题反思，开阔思维;错题反思，优化思维.

[关键词] 反思;思维;解题

随着新课改的落实与推进，再创造、自主探究、独立思考与反思建构等新教育理念日趋成熟. 如何将这些理念切实落实到课堂教学的各个环节，是笔者近两年一直在思考与探索的问题. 实践证明，反思性学习对学生的可持续性发展具有其他理念无法替代的重要作用.

[⇩] 反思性学习的理论与现状

反思性学习是指在学习过程中加以反思的学习，而反思则属于心理学范畴内元认知的领域. 科尔伯格在建构主义理论中提出：“学习不应该是被动接受的过程，而是在各种教学活动中不断概括、反省与抽象的过程[1].”可见，反思在教学中具有举足轻重的作用，其特殊性是无法通过其他方面进行替代的.

纵观当下的高中数学课堂，仍有部分教师尚未转变教学观念，依然试图利用“题海战术”来训练学生的数学思维. 这种方法与教育的初衷往往背道而驰，导致了部分学生思维僵化，无法灵活运用所学知识，更无法形成缜密的思维. 想要改变这一现状，唯有更新教师的教学理念，将“注入式教学”转变成“反思性教学”，使得学生从“要我学”逐渐转变为“我要学”的状态.

[⇩] 反思性学习的实施

波利亚认为：“数学学习就是要学会解题，且不仅要能解标准题，还要能解决各种需要思考、具有创造性的题目[2].”解题作为数学学习的活动形式，反思贯穿于解题的每个环节. 反思性学习是对原有认知进行再发现与检验的过程，具有显著的创新性与研究特征. 良好的反思可促进知识之间的沟通与联系，实现建构主义提出的同化与迁移，从而形成高阶的数学思维与认知结构.

1. 审题反思，缜密思维

众所周知，审题在解题中具有重要地位. 但学生的审题观念一直不容乐观，观察学生的错题，发现很多错误都是由于没有仔细审题而导致的. 有很大一部分学生是边写边读题，下笔匆匆、漏洞百出，之后再因为错误形成的原因（看错条件、抄错数据等）而追悔莫及. 因概念混淆、读题不仔细、看错条件或计算失误等问题而出错无不反映出正确审题的重要性.

因此，加强解题中对审题的反思势在必行. 教师可引导学生在审题时，通过读、问、想等方式看透题意. 尤其要注意对题中所出现的关键词语和数据信息的梳理，加强审题过程中的反思，以确保解题的完整性和正确率. 只有完全弄清试题的背景与题意，挖掘出条件与结论之间的内在联系及隐含信息等，才能实现真正意义上的解题.

例1 非空集合A关于运算⊕满足以下两个条件：①对任意a，b∈A，均有a⊕b∈A;②有e∈A，让对一切a∈A，均有a⊕e=e⊕a=a，称A关于运算⊕为融洽集.

现有以下运算与集合：①A={非负整数}，⊕是整数加法;②A={偶数}，⊕是整数乘法;③A={二次三项式}，⊕是多项式加法;④A={平面向量}，⊕是平面向量加法;⑤A={虚数}，⊕是复数乘法.

问题：A关于运算⊕为融洽集的有哪几个？

审题：第①个A={非负整数}，⊕是整数加法，同时满足对任意a，b∈A，均有a⊕b∈A. 令e=0有a⊕0=0⊕a=a，因此①是符合融洽集条件的;第②个A={偶数}，⊕是整数乘法，若存在a·e=e·a=a，则有e=1∉A，因此②不符合融洽集的条件;③④⑤的分析略. 以此类推，逐个进行分析，可得①④符合A关于运算⊕为融洽集的要求，其他均不符合.

反思：本题属于信息类的创新题，在题设条件中构造了一个新的集合，命名为“融洽集”. 看似难以下手的题目，其实就是为了考查学生审题与分析问题的基本能力. 学生只要理解该新定义所蕴含的规则，再从有理数、多项式、向量等的运算规则出发，逐个进行分析，就可解决问题. 若囫囵吞枣地审题，则求解本题很容易出现错误.

2. 解题反思，开阔思维

笛卡尔提出：“要在解题实践中，通过不断地反思来体验解题方法，并在总结与提炼中获得相应的数学思想[3]. ”解题过程中，教师应引导学生常反思自己对题目的认知，积极地实时监控自己的解题意识状态，体验解题策略、过程与方法，以促进解题能力与反思能力的提升.

简而言之，就是鼓励学生加强对解题过程的反思. 教师可引导学生回顾自己解题过程中的每个过程及心理活动，说说自己刚开始是怎么想的;然后遇到了什么障碍;为什么会遇到这样的解题障碍;从中能吸取到什么规律性的经验;当之后能正确解题时，自己做了些什么调节等.

例2 某次家校活动，学校邀请了6位具有代表性的同学的父母参与活动. 在介绍经验环节，学校将邀请这12位家长中的4位家長（恰巧有2位是夫妻）介绍家庭教育经验，请问有多少种选择方法？

看到问题，有学生快速给出480种的答案. 同时，另一名学生当即反驳：“应该是120种”. 学生对这个问题的兴致很高，为了培养学生自主探索与反思能力，笔者趁机鼓励学生将自己如何获得答案的过程复述一遍，并到黑板上写下计算过程.

在笔者提出复述要求后，学生首先充满热情地在组内进行讨论. 其中，提出480种与120种选择方法的两位同学在复述过程中，都发现自己的答案不正确，并自主找到问题的症结点. 待各组讨论完毕并理顺本题的解题思路之后，各小组派代表到黑板上写出下列计算过程：

①C-C-24C==240;②C=240;③C（C-C）=240;④CCP=240;⑤CCCC=240;⑥CCC=240.

学生在逐个介绍自己的解题方法时，甚至出现了笔者都没有考虑到的方法. 整个课堂学习氛围非常好，很多学生都感叹于其他同学数学思路之广阔. 对于本题的解题过程，笔者完全放权给学生，让学生在讲解中不断反思自己的解题思路是否正确. 如此，既让学生自主发现问题出在哪儿，又拓宽了学生解题的视野，为创新意识的培养奠定了基础.

解题中，笔者鼓励学生反思自己的解题过程，不仅培养了学生的数学综合能力，还提升了学生的元认知能力. 学生在解题反思中，激发潜能、拓宽思维，促使自己形成可持续性发展的学习能力，这体现了数学核心素养的落地.

3. 错题反思，优化思维

错误对学生来说是家常便饭，时有发生. 面对错误的态度，决定了学生在数学道路上的深度与远度. 之所以会发生错误，就是因为错误产生的原因不明显. 因此，教师应在适当的时候给予学生一定的引导或点拨，让错误的原因暴露在学生的元认知体验处，使得他们对此产生反思，以弥补知识或思维上的不足.

例3 求不等式（x-6）≥0的解集.

本题有学生获得的解为{xx≥6}. 面对这个解，笔者提出以下两个问题供学生反思：①能不能将这个不等式的两边同时除以？②大家仔细观察，看看它有没有什么特殊性.

经笔者的点拨，学生进行了总结与反思，自主获得错误产生的原因在于：①存在值为0的特殊情况，因为没有搞清楚此式的真正意义，解题自然会出现错误;②在解不等式或方程的时候，不可在两边同时乘以或除以包含未知数的代数式. 学生经自主总结、反思后获得本题的解为：{xx≥6或x=3或x=2}.

经过反思产生错误的根源，学生不仅自主找出知识的漏洞与思维上的薄弱点，还学会了探寻问题产生的根本原因，总结提炼出解题规律与方法. 这使得学生的反思能力与数学思维品质在错题中得以优化与提升，真可谓吃一堑长一智.

总之，反思性学习实施得越及时、全面、深刻，对学生认知结构的训练则越到位. 在教学的各个环节，有机地渗透反思性学习的理念与意识，能有效地促进学生自我监控力的发展，让学生更加积极主动地参与学习活动，从真正意义上实现新课标所倡导的“反思建构”的教育理念.

参考文献：

[1]  赵冬玲. 建构主义理论指导初中数学教学的研究与实践[D]. 东北师范大学，2003.

[2]  波利亚. 怎样解题[M]. 阎育苏译. 北京：科学出版社，1982.

[3]  曹一鸣，王仲英. 略论数学反思能力的培养[J]. 中学数学教学参考，2004（09）：1-3.

3722501908224