竖直振动无黏液滴的法拉第不稳定性分析1)

刘德华 黎一锴

(北京理工大学机械与车辆学院,北京 100081)

引言

当液滴置于沿竖直方向上下振动的壁面上,其表面会产生不稳定的Faraday 波.这种不稳定现象广泛存在于喷涂加工[1]、喷墨打印[2-3]、超声雾化[4-5]和声场悬浮[6-8]等诸多工业应用中.因为其中涉及到各种有趣的物理现象,如液体表面的模态选择[9-10]、时空混沌[11-12]和液体雾化[13],所以学者们从理论分析[14]、实验[15]和数值模拟[16]等方面对Faraday 不稳定性进行了广泛研究.

Faraday 不稳定现象最早由Faraday[17]在实验中发现,他观察到液体表面波的振动频率是振动基板振动频率的一半或者与其相等.这一规律首先被Benjamin 和Ursell[18]解释,他们使用了线性无黏假设的Mathieu 方程来描述液体平面Faraday 波的振幅增长情况.但是Benjamin 和Ursell[18]的理论无法解释黏性流体的实验现象,直到Eisenmenger[19]将线性阻尼项添加到Mathieu 方程中,才解释了黏性的影响.Kumar 等[20-21]将Floquet 理论应用到线性化的N-S 方程中,进一步地研究了Faraday 不稳定性中的黏性耗散问题,得到的振动加速度振幅的阈值与实验结果一致.

除了平面液层外,液滴的Faraday 不稳定性也非常值得关注.Rayleigh[22]首先推导出了无黏液滴的自由振荡频率表达式,发现表面张力是液滴表面维持在平衡位置的恢复力.后来,Chandrasekhar[23]探究了自然振荡中液滴的黏性效应,发现液滴边界层内的黏性耗散效应是液滴表面振荡衰减的原因.相比于液滴的自由振荡,引入外力的液滴振动系统得到了更广泛的关注.Terrones 和Corrara[24]对恒定径向加速度作用下的球形液滴R-T 不稳定性进行了线性分析.Li 等[25]研究了在任意径向加速度作用下的黏性液滴的R-T 不稳定性,推导出了耦合不同球模的递推色散关系,从理论上确定了稳定液滴的临界尺寸、最不稳定模式及其增长速率.Ebo-Adou 等[26-27]利用Floquet 分析,从理论和数值模拟两方面研究了受时间周期径向加速度的液滴Faraday 不稳定性,但是他们的研究主要聚焦于单流体问题上,忽略了环境流体的影响.吴清等[28]进一步考虑了环境流体可压缩性的影响,发现环境流体的可压缩性会促使液滴破碎.Li 等[29]则考虑了环境流体的密度的影响,发现增加液滴周围环境流体的密度将缩小可能激发的球模范围.姚慕伟等[30]则将Faraday 不稳定性的研究从黏性液滴拓展到黏弹性非牛顿液滴,发现零剪切黏度和应变驰豫时间的增加具有抑制液滴表面波增长的作用,提高了使液滴表面发生谐波不稳定的激励幅值.

本文利用Floquet 方法,将前人对Faraday 不稳定性的研究从径向加速度拓展到竖直加速度,推导得到了液滴表面波线性增长率与模态数以及流动参数之间的色散关系,并对液滴的中性稳定边界在竖直激励与径向激励情况进行对比分析,得到了仰角θ 对中性不稳定边界的影响规律,丰富了液滴Faraday不稳定性的理论研究.

1 理论求解

1.1 物理模型和控制方程

本文建立的物理模型如图1 所示.将坐标系固连在基板上,假设液滴整体受到一个随时间周期变化的均匀惯性体积力的作用;另外,本文的物理模型不考虑动态接触角的影响,这个假设在高频振动(～ kHz)范围内液滴表面波波长远小于液滴尺寸时也是近似合理的.液滴的物理模型用到其他假设和条件如下:环境气体密度远小于液滴密度,忽略环境气体的影响;液滴为不可压的无黏流体;液滴为标准的半球形.

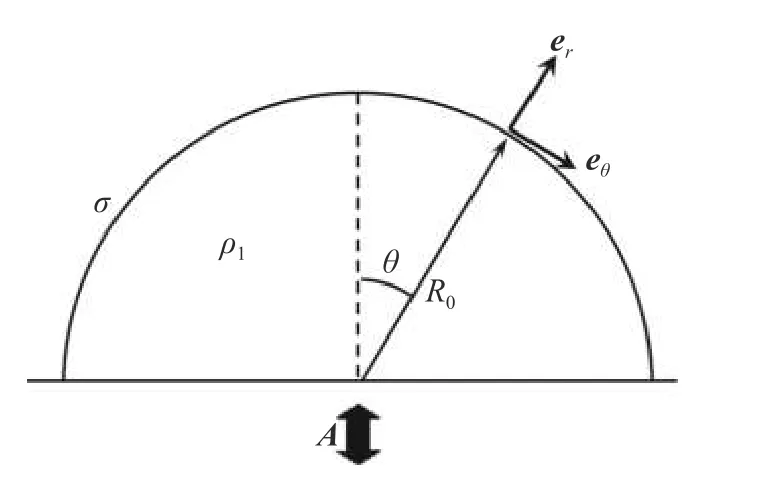
图1 液滴受竖直振动示意图Fig.1 Schematic diagram of a droplet subjected to vertical oscillation

ρ 为液滴密度,σ 为表面张力系数,R0为液滴初始半径,r 和θ 分别为球坐标系中的径向距离和仰角,θ ∈[0,π/2],er和eθ分别为径向和仰角方向上的单位向量.液滴加速度A 在球坐标系下表示为

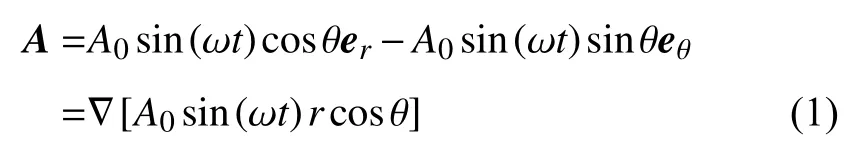
其中,A0为加速度振幅,Ω=2πf 为角频率,f 为惯性力频率,t 为时间.

液滴内不可压缩无黏流体运动的控制方程为

其中u 是速度矢量,p 是压力.

液滴球形表面的表达式为

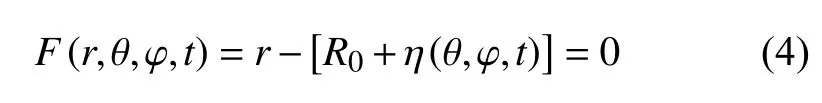
其中,η(θ,φ,t) 为液滴表面的扰动位移,φ 为球坐标系中的方位角.

液滴表面的运动学边界条件为

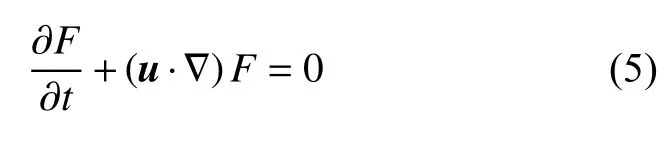
将方程(4)代入方程(5)中,得

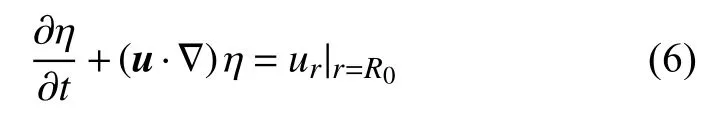
其中,ur是速度矢量u 的径向分量.

由液滴球形表面上法向和切向方向上的应力平衡条件,可得液滴表面的动力学边界条件.液滴表面法向方向上的应力平衡方程为

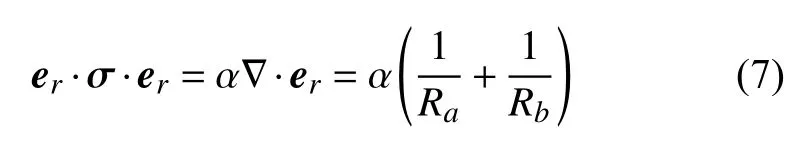
其中Ra和Rb是曲率半径,σ 是应力张量

其中,I 是单位向量.

液滴表面切向方向上的应力平衡方程为

其中,ej=eθ或eφ分别表示液滴表面对仰角方向和方位角方向的单位矢量.

1.2 控制方程和边界条件的线性化

对初始静止状态的控制方程线性化,为了书写方便,仍用u 表示扰动速度,并代入控制方程和边界条件中;忽略动量方程中的非线性对流项.从而得到线性化的流体流动的控制方程为

对液滴表面的运动学边界条件方程(6)进行线性化处理,得

对于法向方向的动力学边界条件,将方程(8)代入方程(7)中,得

其中,曲率半径满足

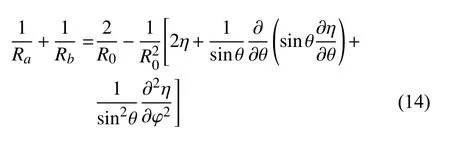
从而使η 达到一阶精度.将方程(14)代入方程(13)中,得到法相方向上线性化的动力学边界条件

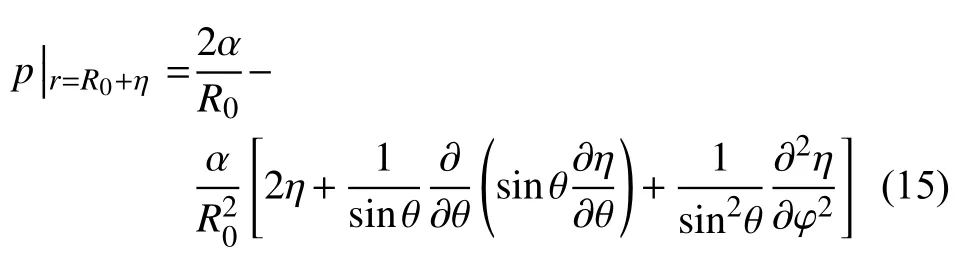
将液滴表面的扰动位移 η(θ,φ,t) 看作是由一系列球谐函数叠加而成,l 和m 分别为球谐函数中的级数和阶数.则扰动位移可表示为

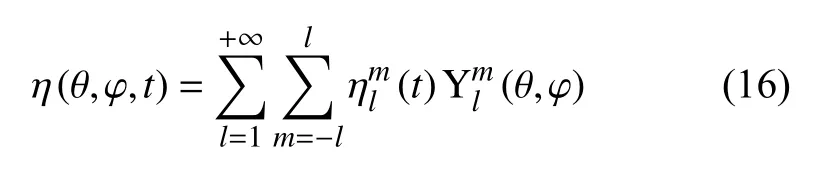
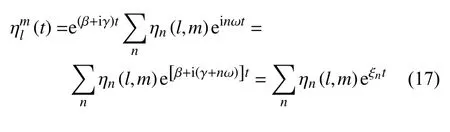
其中,ηn(l,m) 是n 阶Fourier 系数,β+iγ 是Floquet指数,n 是Fourier 阶数,而 ξn≡β+i(γ+nω) 的实部,即β,可视为增长率.

将方程(17)代入方程(16)中,得到扰动位移的表达式为

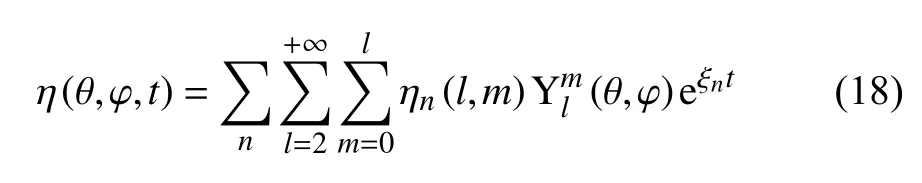
其中,因为当l=0 时,对应液滴整体膨胀或收缩,违反质量守恒定律,所以不予考虑;当l=1 时,对应液滴的移动,而非表面变形,所以也不予考虑.

从而,方程(18)与线性化的控制方程(10)和(11)和线性化的边界条件(12)和(15)构成了一个关于ξn的本征值问题,通过求解这个本征值问题的非零解,可以得到线性增长率 ξn与模态数(l,m)及流动参数之间的色散关系.

1.3 线性化问题的求解

无黏液滴内部的速度势函数 φ 满足u=∇ φ,代入液滴内部的连续性方程(10)中得到

在球坐标系中,考虑到φ 的解在r=0 时不发散,则方程(19)的通解为

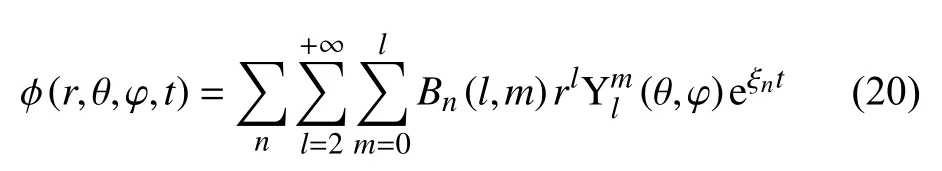
其中,Bn(l,m) 为待定系数.将方程(20)代入液滴表面运动学边界条件(12)中,得到

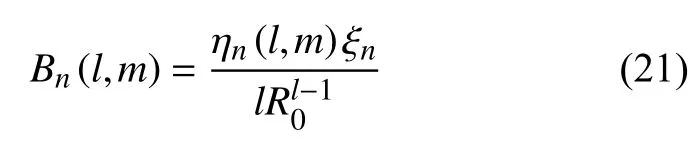
对液滴的动量方程(11) 在径向方向上积分,得到

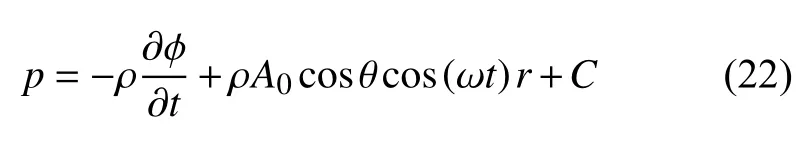
其中,C 是时间函数的积分常数.

将方程(21)和(22)代入方程(20)中,得到液滴表面的压强分布

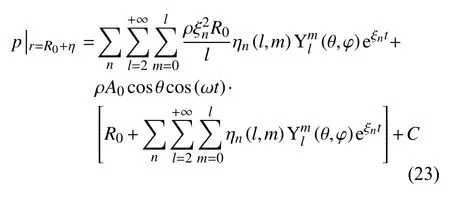
1.4 色散关系

分别由分离变量法以及方程u=∇ φ、式(21)和式(22),可以得到

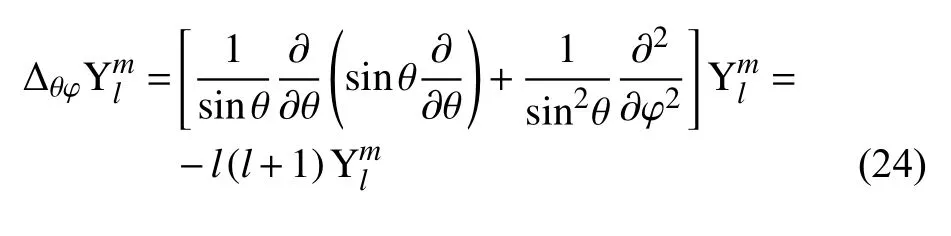
将液滴表面压强分布方程(23)和方程(34)代入液滴表面法向方向上线性化的动力学边界条件(15)中,得

方程(26)为无黏不可压的半球形液滴作正弦运动所引起的Faraday 不稳定性的解析解,也表征了液滴表面波线性增长率 ξn与模态数 (l,m) 以及流动参数之间的色散关系,其中,m 的影响在cosθ 中体现.

2 结果与分析

2.1 无黏液滴的中性稳定边界

将扰动位移的表达式(18)与方程(26)联立,可以得到类似于Mathieu 方程的形式

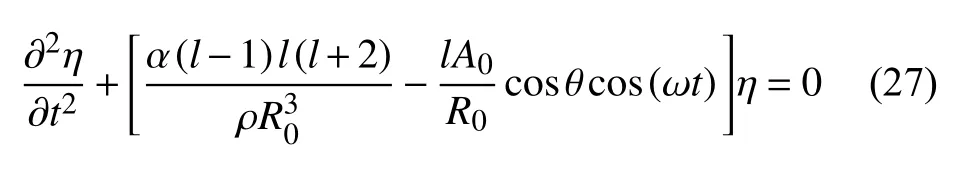
方程(27)与标准Mathieu 方程相比多了与空间有关的cosθ 项,为了分析方程(27)的解的情况,需要将方程中与空间有关的cosθ 项、与时间有关的cos(ωt)项和扰动位移表达式(18)中的系数进行耦合.

根据勒让德函数关系,有

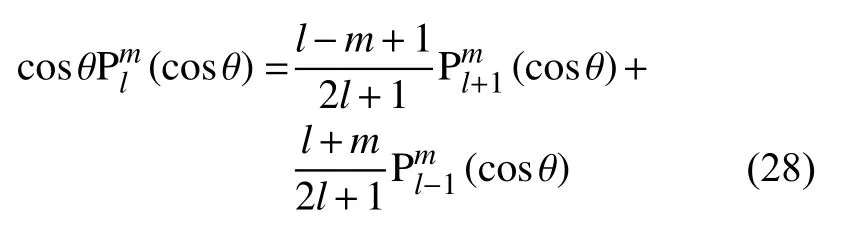
结合上式,由傅里叶变换可得

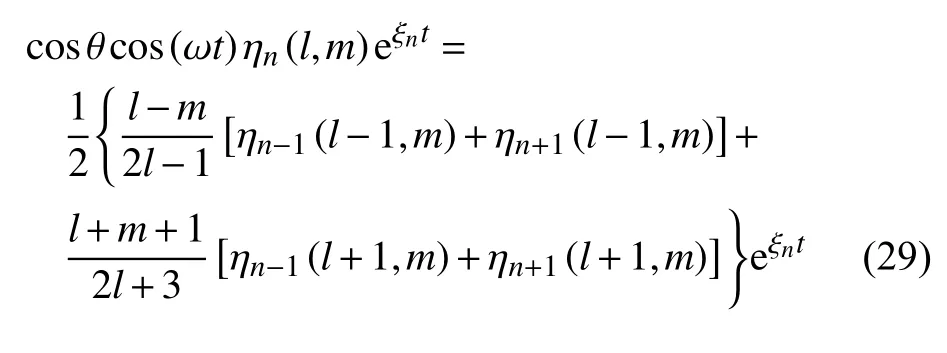
本文的目的主要是比较液滴竖直振动与径向振动的区别,径向振动液滴的情况参考了文献[26].在该文献中的模型为轴对称的液滴,即m=0,因此在本研究中,同样取m=0.此时,系数 ηn(l,m) 退化为

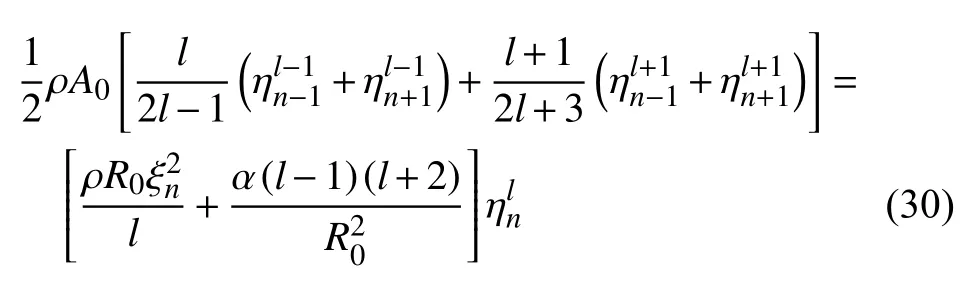
对于不稳定问题,首先要考虑的是稳定和不稳定之间的边界或临界值.在以往关于径向加速度作用下球形Faraday 不稳定性的研究中,这个边界可以通过求解无穷维系数矩阵的本征值得到.在本研究中采用了类似的方法.

当 Re(ξn)=0 时,液滴表面保持中性稳定.为了确定中性稳定的边界,根据 ξn=β+i(γ+nω),令 β=0,方程(30)可化为

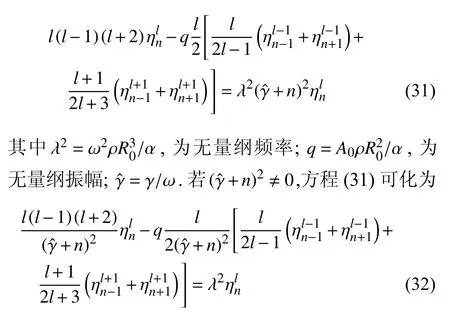
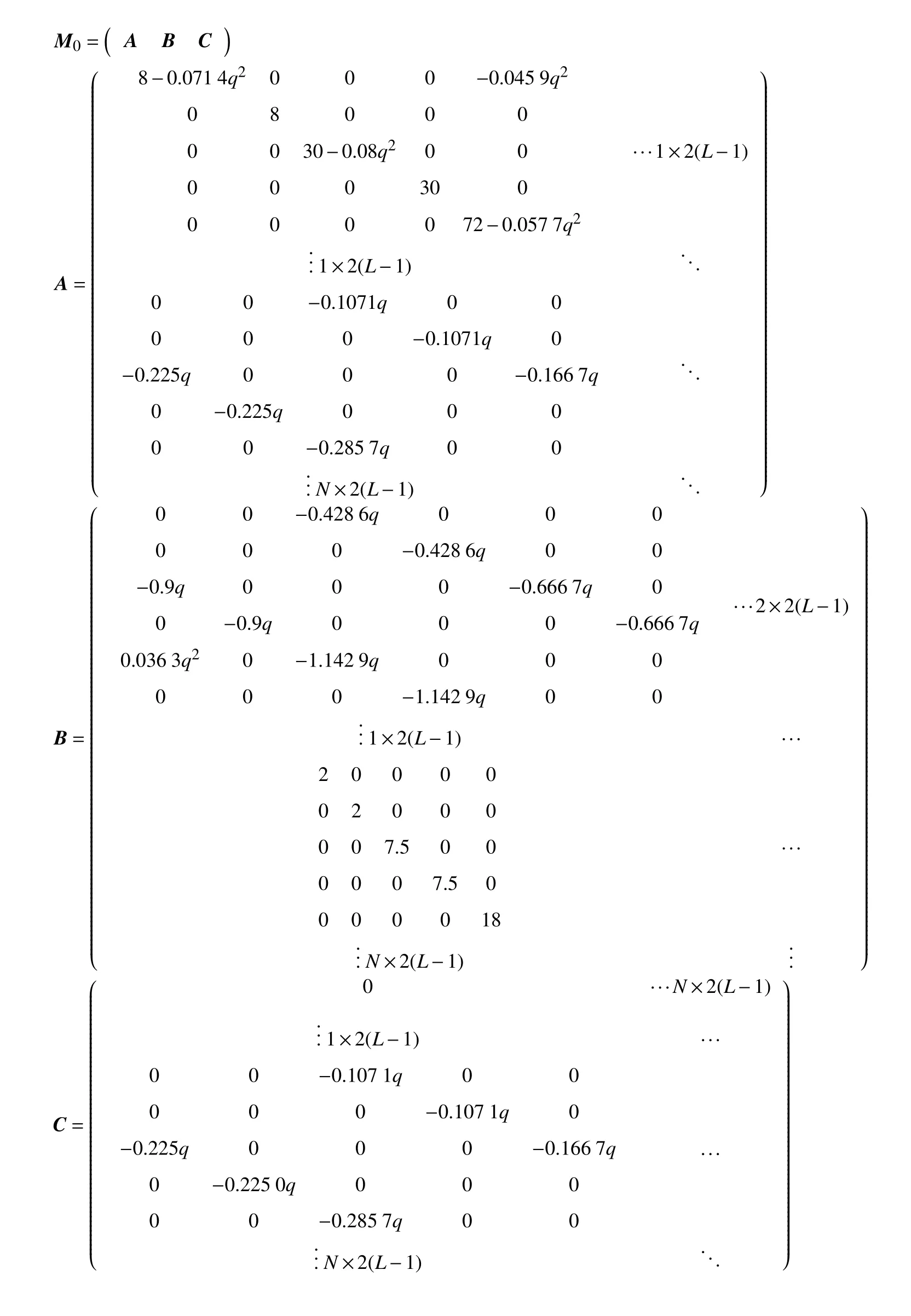
将方程(32)按实部和虚部展开,并写成矩阵的形式:M x=λx,其中,M 为特征矩阵,λ 为特征值,x 为由的实部和虚部所组成的列向量.

当 γˆ=0 时,M 为 2n×(l-2) 阶方阵,x 为2n×(l-2)维的列向量.因为n 不等于0,而当n=1 时,系数中会出现,所以需要利用方程(32)得到的表达式

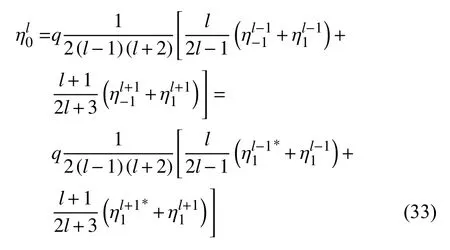
通过求解不同q 值下矩阵M 的特征值,即可得到无黏液滴在 λ -q 坐标系下的中性稳定边界.虽然M 为无穷维的实矩阵,但是随着n 和l 的增加,低阶的特征值将趋于收敛.因此,通常选取足够大的N和L 来截断M,从而求解M的特征值.实际情况下总是出现亚简谐(n=0)和一阶简谐(n=1)不稳定性.出于重点关注液滴低阶不稳定性的目的,本文选取N=5,L=10,此时,较小n 和l 已经收敛.

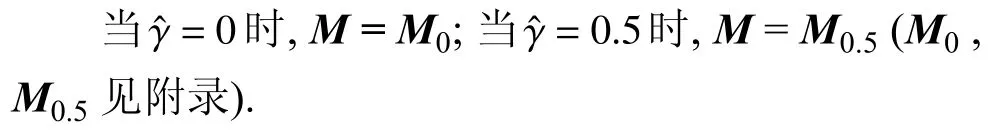
图2 为 λ -q 坐标系下无黏液滴的简谐不稳定图.纯直线表示竖直振动液滴的不稳定边界,直线带圆点标记的表示径向振动液滴的不稳定边界.中性不稳定边界将 λ -q 坐标平面划分成若干稳定区域和不稳定区域,并且中性稳定边界与λ轴相交于其中l=2,3,4,··· .当(λ,q)位于不稳定区域,液滴表面模态将产生不稳定.

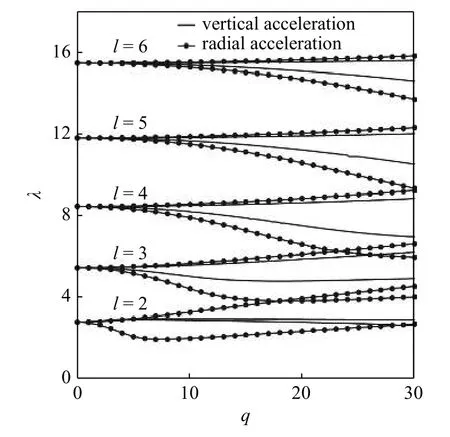
图2 径向振动和竖直振动的液滴简谐不稳定边界对比图Fig.2 Comparison diagram of droplet harmonic instability boundary subjected to vertical and radial oscillation

由图2 可知,即使当q 非常小,即实验中的加速度振幅非常小时,仍然存在组合 (λ,q) 使液滴表面产生不稳定.另外,竖直振动的液滴表面波不稳定区域要明显小于径向振动的,且前者基本被后者包含,这就意味着在 q 一定的情况下,使液滴表面产生特定不稳定模态的λ 的取值范围变窄.尤其是对于 l=2 的情况,竖直振动的液滴表面波不稳定区域的上下边界线几乎重合在一起,在实际的实验中将很难出现这种不稳定模态.

另外,径向振动液滴的各不稳定区域之间会出现重叠,当组合 (λ,q) 位于重叠区域时,表面波会出现不同模态间的竞争和转捩.而竖直振动的液滴,在较小的q 值下,各不稳定区域之间不会出现重叠.

图3 为 λ -q 坐标系下无黏液滴的亚简谐不稳定图.纯直线表示竖直振动液滴的不稳定边界,直线带圆点标记的表示径向振动液滴的不稳定边界.不同于图2 的是,竖直振动液滴的表面波不稳定区域的边界重合在一起,这意味着液滴表面不会出现亚简谐的不稳定波.

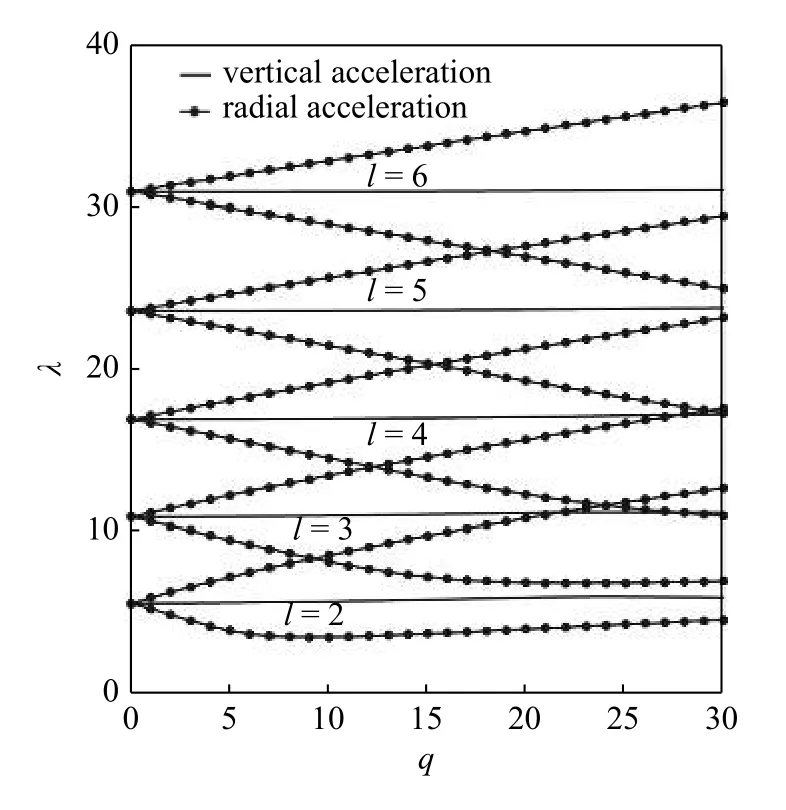
图3 径向振动和竖直振动的液滴亚简谐不稳定边界对比图Fig.3 Comparison diagram of droplet subharmonic instability boundary subjected to vertical and radial oscillation

竖直振动的液滴与径向振动相比,二者差别明显,其差异表现为 简谐情况时,液滴表面波的不稳定区域变小,液滴在受到外部激励时将更难失稳;亚简谐情况时,液滴表面波的中性稳定边界重合在一起,液滴不稳定波将难以出现亚简谐模态.

从振动形式来看,径向振动液滴的不稳定表面波的振动情况可以看作是参数振动,而竖直振动液滴所出现的表面波振动频率与外加振动频率相同的情形近似为受迫振动时的情形.

对于附着在固壁上的半球液滴,需满足无穿透条件,使得级数l 和阶数m 满足条件:l+m 为偶数[31].也就是m=0 或者其他偶数时,l 取偶数的解才有物理意义;m=奇数时,l 取奇数才有物理意义.但是对于本研究中的模型,壁面只是施加惯性力的媒介,因此,在m=0 时,l 取奇数的解依然具有一定意义.

2.2 对空间参数θ 的近似计算

竖直振动的液滴,其表面的加速度可以分解成沿径向的分量和沿切向的分量,这就使得液滴表面的Faraday 波不仅随时间周期变化,而且在空间上也是不均匀的.这种空间上的不均匀主要受仰角θ 的影响,为了更加直观地体现空间上的不均匀性,本文对空间参数θ 在大模态数下进行了近似计算.

保留方程(25)中的空间相关项cosθ,由傅里叶变换得

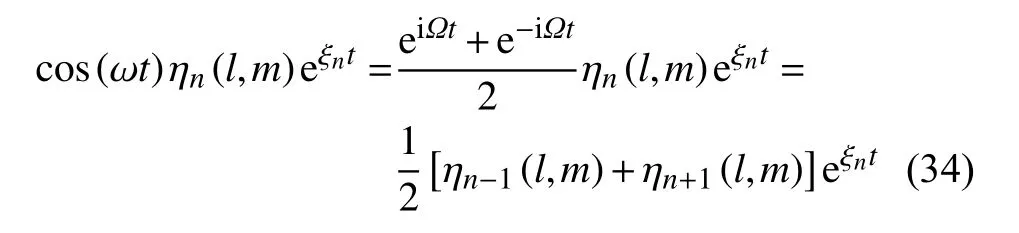
省略 ηn(l,m) 中的 (l,m),将方程(34) 代入方程(25),并根据的线性无关性,最后得到

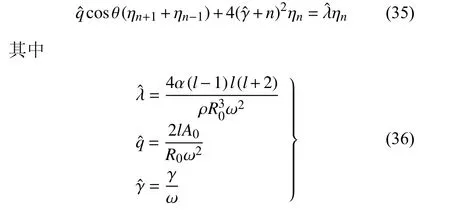
由图4 和图5 可以直观地发现,仰角θ 对于中性稳定边界的影响体现为 θ=0 处的Faraday 不稳定边界图与径向振动液滴的相同;随着仰角θ 的增大,不稳定区域的边界逐渐收窄,不稳定区域减小,意味着各种不稳定模态更难出现;当 θ=90°时,竖直加速度沿径向的分量为0,不满足Faraday 不稳定出现的条件,因此其图像表现为不稳定区域的上下边界重合在一起.

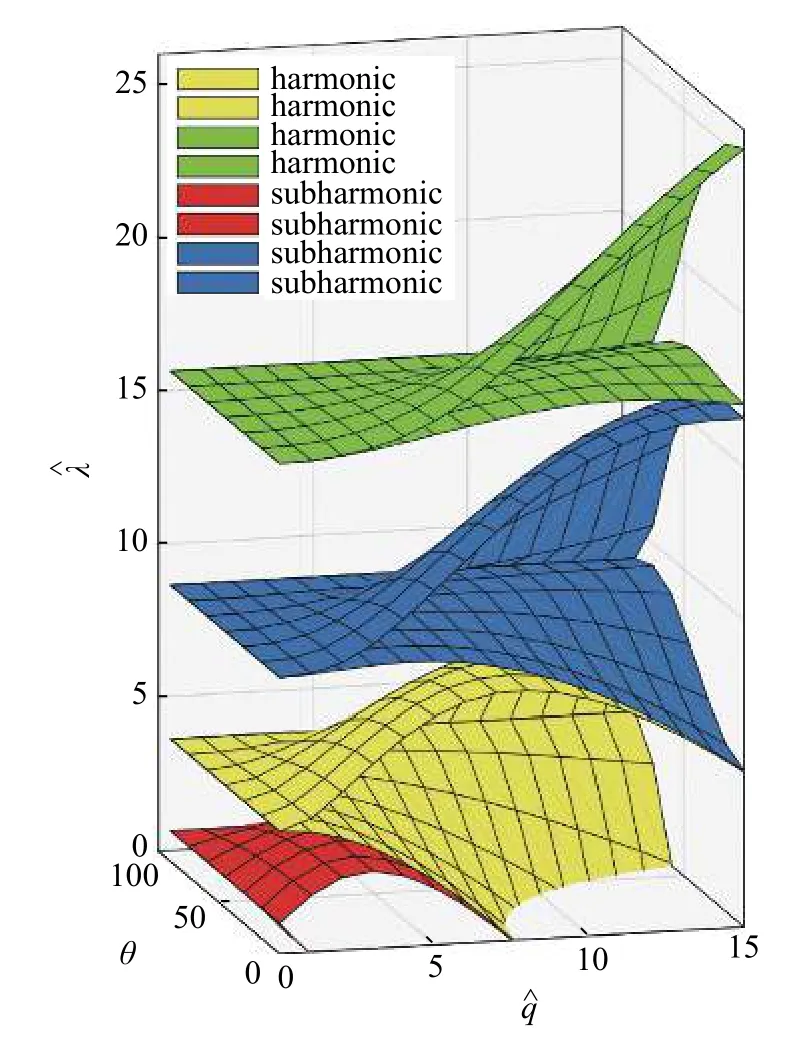
图4 --θ 空间坐标系下第一象限的Faraday 不稳定边界图Fig.4 Faraday instability boundary diagram of the first quadrant in --θ space coordinates

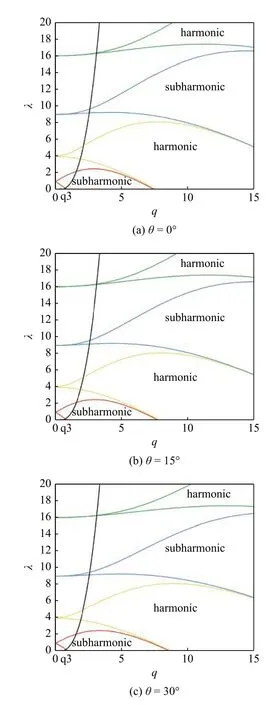
图5 (a)-(g)分别为 θ=0°,15°,30°,45°,60°,75°,90° 时的中性稳定边界图Fig.5 (a)-(g) are neutral stability boundary diagrams when θ=0°,15°,30°,45°,60°,75°,90°,respectively

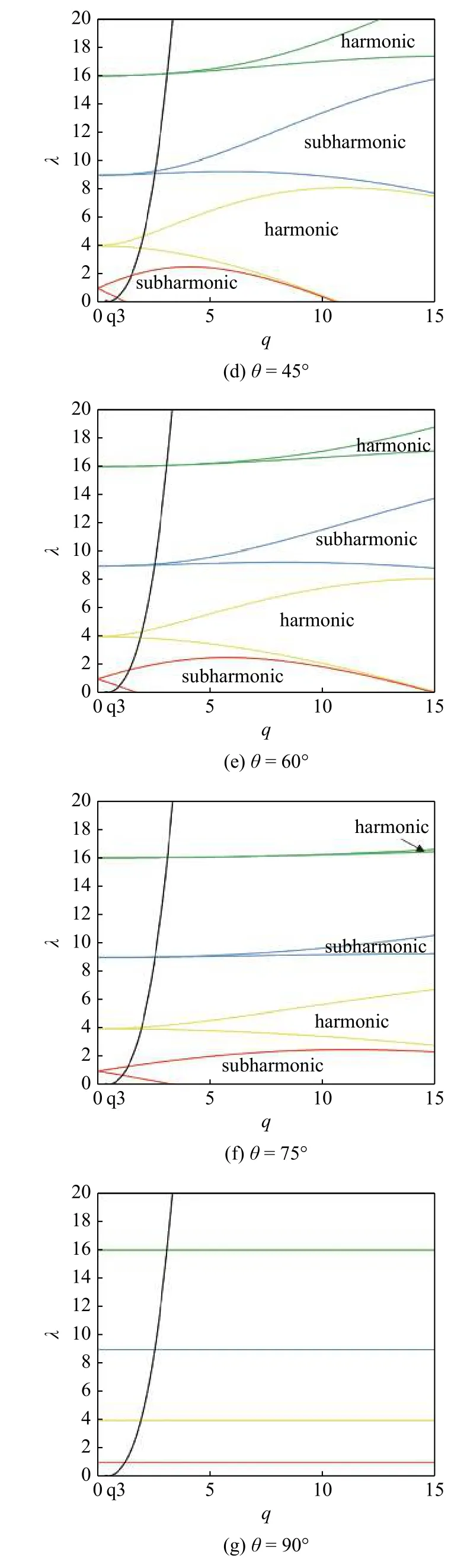
图5 (a)-(g)分别为 θ=0°,15°,30°,45°,60°,75°,90° 时的中性稳定边界图(续)Fig.5 (a)-(g) are neutral stability boundary diagrams when θ=0°,15°,30°,45°,60°,75°,90°,respectively (continued)

竖直振动的液滴,其表面Faraday 波的空间不均匀性的直观体现为随着仰角θ 的增大,当地的液滴表面变得更稳定.而通过2.1 节的理论分析结果来看,空间不均匀性导致了表面波亚简谐模态的消失,使得竖直振动的液滴表面波,只会出现简谐模态.

3 结论

本文对受时间周期竖直加速度的无黏液滴的Faraday 不稳定进行了线性分析,得到的主要结论如下.

(1)利用Floquet 方法,得到了液滴表面波线性增长率与模态数以及流动参数之间的色散关系,基于Mathieu 方程的求解方法,得到了无黏液滴在Faraday不稳定性下的中性稳定边界.

(2)竖直振动的液滴与径向振动的液滴相比差别明显:简谐情况下总体的不稳定区域较小,说明液滴在受到外部激励时将更难失稳;亚简谐情况下的不稳定边界重合在一起,液滴不会出现亚简谐的不稳定波.这意味着使液滴表面产生特定不稳定模态的特征频率的取值范围更小,特定的不稳定模态更难激发.

(3)通过对空间参数cos θ 进行近似处理,得到了仰角θ 对中性不稳定边界的影响规律,即液滴表面仰角越大的位置中性不稳定区域越小,在受到外部激励后越容易保持稳定.

附录