转动驱动圆角立方体颗粒有序堆积的离散元模拟1)

张 祺 乔 婷 季顺迎 厚美瑛

* (中国科学院物理研究所,北京 100080)

† (太原理工大学机械与运载工程学院,太原 030024)

** (大连理工大学工业装备结构分析国家重点实验室,辽宁大连 116023)

引言

热系统中无序的粒子在热驱动下进行重新排列,自发形成有序的结构,称为自组装过程[1-2].作为非热学流,尽管热运动对颗粒物质的影响可以忽略(mgd≫kBT),但容器的振动[3-5]、旋转[6]、敲击[7]、剪切[8-9]以及重力驱动下自身流动[10]也可以发挥热涨落的驱动作用,改变颗粒体系的构型,达到整体或者部分颗粒有序堆积的效果.宏观颗粒有序堆积过程为研究微观粒子系统自组装问题提供了很好的借鉴.

颗粒的有序堆积必然伴随颗粒系统的密实化过程,这不仅涉及拓扑结构、对称性等颗粒系统结构优化问题,而且对提高交通运输、包装工业、工农业生产中颗粒材料的空间利用率具有重要现实意义[11].研究发现三维单分散球体的最密随机堆积(random close packing,RCP)体积分数约为0.64[12-13],更高体积分数尤其是最密规则堆积的三维单分散球体结构则需要一些繁复的方法才能实现.Carvente等[14]利用一种类似退火的方式(振动强度逐渐降低)实现了三维方形容器中的等大钢球从初始的颗粒气体状态逐渐形成体心四方或者面心立方结构.Yu 等[15]通过一个类似晶体外延生长的方式向振动颗粒床中逐步添加球体最终实现了三维的最密规则堆积结构.Shinde 等[16]使用混合蒙特卡罗算法模拟等大球在振动下的自发结晶化过程,发现较低振动强度下结晶化只会在局部区域出现而不能实现全局结晶化,而高振动强度时结晶化过程表现为六方最密堆积结构和面心立方结构的竞争.然而现实世界中真实颗粒多是非球形的,非球形颗粒与球体颗粒的堆积性质存在较大的差异.其中一个主要原因是非球形颗粒接触形式远比球形颗粒接触更加复杂,包括面-面、边-面、边-边和顶点-面4 种基本接触形式[17].这促使人们开始进行关于非球形颗粒堆积性质的研究.

Baker 等[18]通过沉降实验研究了正四面体、正六面体、正八面体、正十二面体和正二十面体共五种柏拉图实体的最密随机堆积(RCP)和最松随机堆积(random loose packing,RLP)的体积分数,发现除了立方体可以实现无空隙的全空间密堆积外,其他四种实体的RCP 和RLP 体积分数均随边数的增加而逐渐下降,实体的摩擦系数越大其RCP 和RLP 的体积分数越低.Donev 等[19]发现不同长短轴的椭球颗粒最密随机堆积体积分数不尽相同,最高可达0.74,此时椭球平均配位数远高于球体.Torquato等[20]通过ASC (adaptive shrinking cell)数值模拟算法指出正八面体最密规则堆积的体积分数约为0.947,正十二面体约为0.904,而正二十面体约为0.836,远高于实验发现的随机堆积体积分数.Börzsönyi 等[21]通过环剪实验发现细长棒状颗粒会自发形成一定取向的规则排列,且同流线之间存在一个特定夹角,该夹角与剪切速率无关.Hidalgo 等[22]通过筒仓中棒状颗粒沉降实验发现,颗粒倾向于以不同的倾角在筒仓中形成有序排列,最可几倾角的大小与颗粒的长径比有关,其中方形颗粒最易以对角线沿重力方向排列.Asencio 等[23]通过容器往复水平旋转的方式而不是传统的振动或者敲击的方式对圆筒容器中的立方体骰子进行旋转剪切,实现了立方体颗粒最密规则堆积,为非球形颗粒的堆积研究提供了新思路.

尽管实验上已经对旋转圆筒中立方体颗粒的有序堆积的研究取得了重要进展,然而由于所研究颗粒体系的复杂性和控制参数的多样性,目前对非球形颗粒有序堆积的细致过程和力学机制的理解还不够深入,需要进一步研究讨论.三维颗粒系统内部结构的实验观测通常是困难的,其力学行为的问题也难以通过实验得到完全解决.离散元方法能够跟踪到每一个颗粒的空间位置,从而可以记录内部结构在介观尺度的细节信息,是对颗粒体系动力学行为实验研究的有力补充[24-26].因此,本文利用离散元方法对旋转圆筒容器内立方体颗粒有序堆积过程进行数值模拟以获取立方体颗粒有序化过程中的结构演变特征,分析了容器运动方式对立方体颗粒有序堆积过程的影响规律,有助于深入理解复杂颗粒系统的结构演化的微观机理.

1 圆角立方体颗粒有序堆积过程的离散元数值方法

1.1 基于超二次曲面的圆角立方体颗粒

超二次曲面形状是二次曲面的延伸,80%的常见非球形颗粒几何形状可由超二次曲面方程描述[27-28].本文所模拟的立方体颗粒具有高度的对称性,因此选用超二次曲面连续函数表示.超二次曲面颗粒的形状表示为

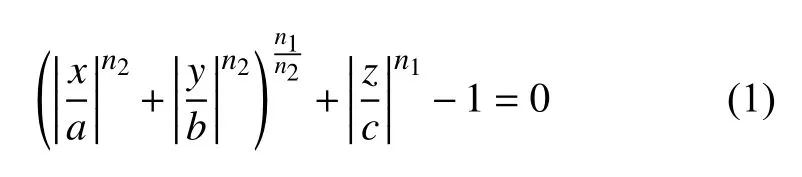
其中,a,b,c分别为颗粒沿主轴方向的半轴长,n1和n2是表征颗粒尖锐度的块效应参数.通过改变式(1)中表征颗粒形状的五个形状参数(a,b,c,n1,n2),可以灵活地获得不同形状的颗粒.当 n1=n2=8,a=b=c 时,即可构造带有较小圆角的立方体颗粒单元.

1.2 圆角立方体颗粒单元间的接触检测

颗粒接触检测的主要内容是检测颗粒是否接触以及确定接触点和接触法向.超二次曲面单元间的接触检测问题可以考虑为一个定义在全局坐标系下连续且二阶可导形状函数的超二次曲面颗粒间最小距离的最优化问题[25,29-30].最优化问题通过设立拉式算子 λ,由下面的拉式函数给出

其中 X=(x,y,z)T,最优化问题的解由∇X,λL(X,λ)=0确定,引入 μ2=(1-λ)/(1+λ),最终简化为四元非线性方程组

确定法向重叠量的牛顿迭代公式可写为

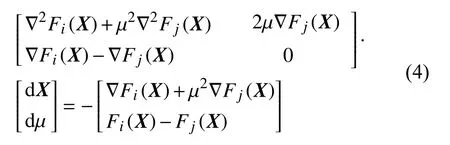
式中,X=X+dX,μ=μ+dμ .计算结果 X0满足Fi(X0)＜0 且 Fj(X0)＜0 则表明两个单元间发生接触.接触法向 n 可表示为n=∇Fi(X0)/||∇Fi(X0)|| .进一步考虑Xi=X0+αn 和 Xj=X0+βn,这里未知参数 α 和β 可通过一元非线性牛顿迭代得到:因此,法向重叠量可表述为 δn=Xi-Xj.

1.3 接触模型及接触力的计算

基于球体的赫兹接触模型和椭球体的表面曲率接触模型,超二次曲面单元的非线性接触力可按照考虑等效曲率的接触模型计算[31].在超二次曲面颗粒的相互作用中,颗粒间的相互作用力可认为是法向接触力和切向接触力的叠加.法向接触力主要包括弹性力和黏滞力,此外非球形不规则颗粒的接触力可能不通过颗粒形心,因此引起的附加弯矩也应被考虑[32].

法向作用力可以表示为

其中,Kn为两个接触颗粒间法向有效刚度,δn为两个接触颗粒间的法向重叠量,Cn为两个接触颗粒间的法向黏性系数,B 为两个接触颗粒间的黏滞系数,vn为两个接触颗粒间的法向相对速度.

法向有效刚度 Kn和黏滞系数 B 可由颗粒材料的弹性模量 E、泊松比 ν 和接触点处的平均曲率半径R 通过下式得到

其中,Ri和 Rj分别表示颗粒 i 和颗粒 j 的等体积球半径,mi和mj分别表示颗粒 i 和颗粒j 的质量.

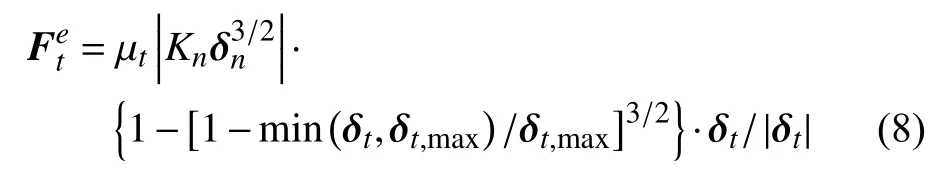
其中,μt为滑动摩擦系数,δt为切向重叠量,

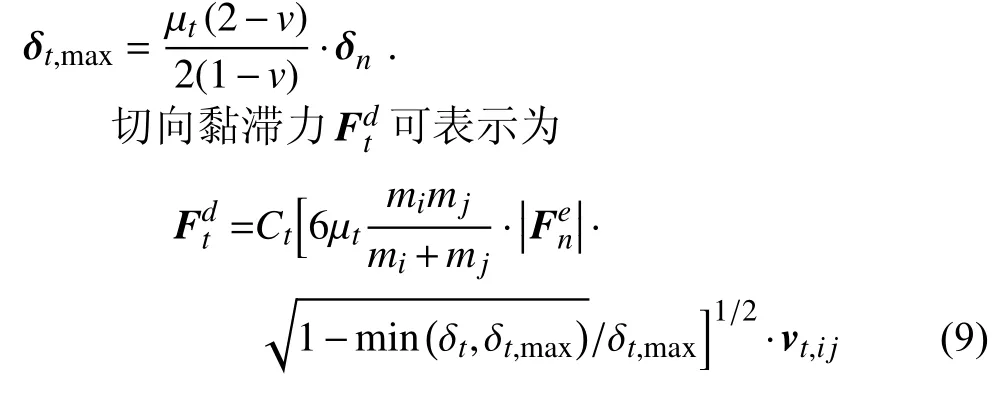
其中,Ct为切向黏滞系数,vt,ij为单元间的切向相对速度.

当颗粒间发生相对转动时,由滚动摩擦引起的力矩可表示为

其中,μr为滚动摩擦系数,=ω/|ω| 为接触颗粒间的单位相对角速度.

1.4 圆角立方体颗粒的运动控制方程

颗粒的运动包括平动和转动,其平动的控制方程为

其中,mi和 Xci是颗粒i 的质量和颗粒质心的坐标,Fi是作用在颗粒 i 上的合外力.

而颗粒的转动遵循动量矩定理为

其中,Ii和 ωi分别是颗粒 i 全局坐标下的惯性矩和角速度,Li是颗粒 i 的角动量,Ti是作用在颗粒 i 上对颗粒质心的总转动力矩.对于非球形颗粒,其惯性矩与颗粒的位向有关,在全局坐标系下,非球形颗粒的惯性矩是一个各个分量都可能不为零的二阶张量,运动的描述十分复杂,而在固定于颗粒本身的局部坐标系中,非球形颗粒的主惯性矩是一个仅对角线元素不为零的二阶张量,运动描述简便.因此,引入可以实现局部坐标系和全局坐标系相互转化的四元数 q 表示颗粒的位向

非球形颗粒的位向通常由全局坐标系 eG向固定于颗粒本身的局部坐标系 eL的转换表示,而四元数q 可以通过转换矩阵 A 实现这种坐标系之间的相互转换

这里转换矩阵满足 A-1=AT,且由四元数确定

根据建立在角动量定理上的欧拉运动定律可以得到局部坐标系下的颗粒转动方程

1.5 圆角立方体颗粒有序堆积过程的实施方案

程序中颗粒所处容器为圆柱形转筒,半径r=0.067 m,高度h=0.17 m.初始时,800 个边长为0.01 m 的立方体颗粒在圆筒上方空间生成,之后以一定速度掉落至容器中并等待直至形成位置和取向均随机的堆积体.通过边界的“往复旋转”向立方体颗粒堆积体传递边界转动产生的剪切作用,如图1所示.离散元模拟中所需的主要计算参数如表1 所示,模拟环境重力加速度为g=9.81 m/s2.转筒边界以一个选定的峰值角速度 ω0进行正反向的循环旋转,边界的切向加速度a 为

表1 转动驱动立方体颗粒有序堆积过程的主要计算参数Table 1 DEM simulation parameters of ordering of cubes

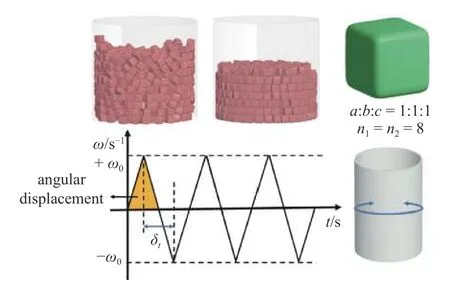
图1 装置示意图以及边界旋转方式Fig.1 Schematic diagram of simulation and boundary rotation mode

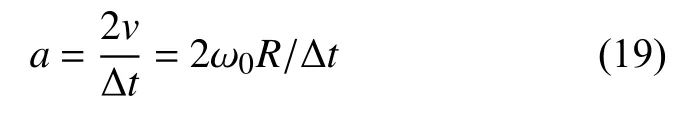
其中R 为圆柱形边界的半径,v 是边界的切向速度,Δt是反转过程需要的时间.使用重力加速度无量纲化后的扭转加速度 γ 为

旋转过程中单向转动的角位移 β 为

在上述模型和计算条件的基础上,借助自主开发的GPU 并行离散元计算程序针对立方体颗粒受转动驱动有序堆积过程进行模拟计算.计算平台为配备英特尔xeon 4210 CPU 和Nvidia Tesla K40 显卡的工作站.由于与球体颗粒相比,超二次曲面单元间的接触判断更加复杂,其采用非线性牛顿迭代算法经多次迭代才可计算出单元间的重叠量.因此,对于非球形颗粒系统,超二次曲面单元比球形单元具有更低的计算效率和更长的计算时间.由于本文研究所模拟的实验过程历时较长,且Asencio 等[23]的实验系统中颗粒数目(25 000 个)对于模拟而言计算耗费较大,因此选取立方体颗粒总数为800 以观察其有序堆积现象.

2 结果与讨论

2.1 立方体颗粒有序堆积的对比验证

Asencio 等[23]的实验证实当圆筒扭转加速度大于一定值时,圆筒内的立方体颗粒会形成密实有序的堆积体.本文的模拟中也观察到了类似的结果,如图1 所示.这里引入两个统计量表征立方体的有序堆积过程.体积分数 φ (填充率)可以描述颗粒体系的密实状态.有序度参量 S4通过立方体颗粒的朝向计算得到,用于定量描述立方体颗粒体系的有序化堆积程度.

体积分数 φ 的一般定义为总颗粒的实际体积除以颗粒堆积体占据的空间体积,即

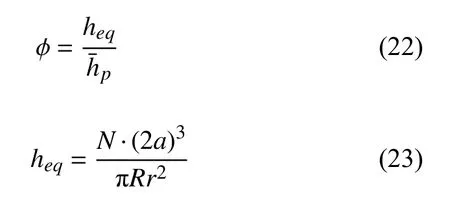
其中,heq是颗粒总体积除以容器底面积得到的等效圆柱体高度,是立方体颗粒堆积体上表面的平均高度.上表面的平均高度的计算方法是将颗粒域划分为一系列适当大小的网格,标记每列网格中(沿容器高度方向的若干网格称为一列)位置最高的颗粒的z 坐标,再对所有列位置最高颗粒的z 坐标求平均值并加上颗粒的半边长修正得到上表面的平均高度式(23)中,N 为颗粒总数,单一颗粒体积按照标准立方体体积计算.其圆角缺失的部分体积根据高斯-勒让德积分公式计算为标准立方体体积的6%,因此式(23)计算得到的体积分数会略大于真实的体积分数.本文选用式(23)计算体积分数是为了与文献[23]的体积分数计算方法保持一致,以便于数值模拟结果和实验结果相对比.

有序度参量 S4[33]为

其中 μi为立方体颗粒i 的表面外法线方向,nb=(0,0,1)T为转筒的转轴方向.一般的超二次曲面颗粒有三个颗粒主轴,而对于具有良好对称性的立方体颗粒,三个颗粒主轴无需进行区分.因此,在数值计算模型中,改进的 S4计算公式为

其方中向 向j=量1,.2m,3a;xe(ieji表j·n示b)颗表粒示i的3 个3颗个粒颗主粒轴主的轴单的单位位方向向量分别与 nb点乘的最大值.数值计算模型中,颗粒各主轴方向由四元数确定,因此,颗粒主轴在全局坐标系下的方向向量为

图2 为 γ=1.01,ω0=5 rad/s 时,φ 和 S4随旋转次数的变化.其中图2(a)为文献[23]的实验结果.如图所示,数值模拟得到的 φ 随旋转次数增加的变化趋势同实验结果所展示的变化趋势基本一致,呈现随着旋转次数对数值的增加逐渐增大直至稳定的特点.这种变化趋势与Nowak 等[34]通过敲击实现球形颗粒随机堆积体系密实化所发现的 φ 的变化规律完全一致.这意味着对于立方体颗粒,容器的旋转剪切扮演了敲击的作用,通过这种简单的人为设计扰动方案可以得到接近立方体颗粒最密规则堆积的结构.本文所得到的体积分数达到最终稳定状态时的数值同实验结果略有差异.本文不同边界运动条件下的数值模拟最终结果均为一个7 层的立方体颗粒堆积体,最上层内的颗粒约为69～72 个,设置这些颗粒是为了保证下部6 层的颗粒数量达到饱和,其他各层颗粒约为119～123 个.若去掉最上层颗粒,φ 的值约为0.88.由于正方体边长去贴合容器边壁时难免有空隙且模拟计算的颗粒数小于实验体系,这也使模拟所得到的 φ 略低于实验值0.96.此外模拟得到的 φ 达到稳定状态后涨落相较实验结果更为明显.这是因为当第六层颗粒填满后,下面六层的排布结构就不再显著地变化,但是最上层的颗粒还会伴随下层颗粒的整体转动产生移动和翻转,对于体积分数的计算结果带来一定的涨落.如果去掉第七层颗粒,体积分数的涨落是非常小的.

图2 体积分数及有序度随旋转次数的变化Fig.2 Packing fraction Φ and cubatic order parameter S4 versus number of rotation

有序度参量 S4随旋转次数增加而呈现的变化趋势与 φ 的变化趋势相同.S4最终稳定在0.95 左右,标志着体系完成了从无序向有序的转变.图中 S4的变化存在一个比较明显的转折点,可以定义一个特征旋转次数 Nr,用于标记体系何时完成有序堆积.相较于实验结果,模拟计算得到的 Nr小一到两个量级,可以认为这是由于离散元模拟所用的颗粒数远小于实验颗粒数目所导致的.数值模拟选取的容器底面直径和颗粒边长比为13.4,而实验中容器底面直径和颗粒边长比约为35.下一小节中,可以清楚地看到,边壁的旋转剪切作用所导致的颗粒体系的密实有序化过程是逐渐的从外侧向内侧演化发展的.模拟仅需要完成4～5 层的颗粒同心圆排列就基本完成有序化过程,而实验则需要完成15 层左右的同心圆排列.考虑到往复旋转边界的扰动影响必然是通过最靠近筒壁的颗粒逐渐向内部传递,因此模拟结果得到的Nr小于实验结果是可以理解的.尽管如此,模拟得到的 φ 和 S4的变化趋势,可以很好地反映立方体颗粒在边界往复旋转作用下的密实化效果和有序化过程,这表明基于超二次曲面颗粒单元的DEM 数值模型的有效性.

2.2 立方体颗粒有序堆积过程的结构演化

图3 给出了 γ=4.04,ω0=10 rad/s 时,立方体颗粒堆积体在侧面、半剖面以及底面视角下的有序化过程.如图所示,初始时刻体系处于随机堆积的状态有序度较低,底面上颗粒分布相对松散.随着旋转剪切次数的增加,几十转内位于顶层的颗粒(蓝色)会不断的通过缝隙掉落至下层颗粒(红色)中,体系将迅速完成主要的密实化过程.同时,靠近底面和容器边壁的颗粒呈现某一面平行容器底面的有序状态,而靠近转轴的内部颗粒则依然处于无序的状态.之后的几百转内,最低的6 层颗粒逐渐填满并全部实现某一面平行容器底面的有序排列,最上一层颗粒则依然会出现移动和翻转.从底面层颗粒的速度分布(彩图)可以看出,最靠近容器边壁的一圈颗粒速度最大,越靠近转轴的颗粒速度越小,颗粒间的速度差会造成颗粒间的切向滑动摩擦力.这证明边壁扰动确实是以摩擦力的形式促使颗粒的有序堆积从靠近筒壁的颗粒逐渐向内演化.

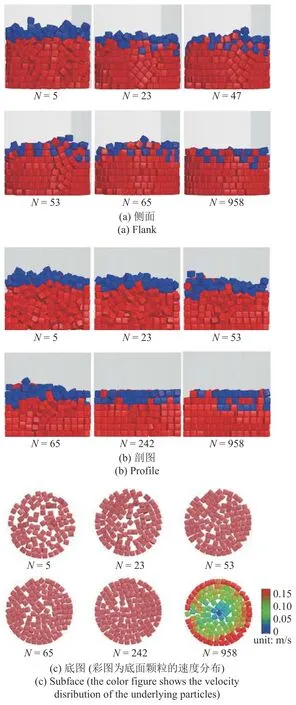
图3 立方体颗粒的有序化过程Fig.3 The ordering process of cubic particles

进一步地细致观察发现初始时刻立方体颗粒完成沉降堆积后,虽然整体的有序度比较低,但是单一颗粒和其相邻颗粒间并不会存在巨大的取向差异.Boton 等[35]研究结果表明,具有平面的非球形颗粒相互接触时,面与面的接触方式最大程度阻碍颗粒的转动且最容易满足颗粒堆积体的稳定性要求,因此具有平面的规则非球形颗粒很容易形成特定方向的排列,对于具有高度对称性的立方体颗粒更是如此.Bautista-Carbajal[36]给出了二维狭缝中方形颗粒的团簇相图,结果表明狭缝中的方形颗粒有三种稳定的状态,分别是边长平行狭缝边界,对角线垂直狭缝边界以及两者的混合状态.对于三维立方体颗粒,Zuriguel 和Maza 等[22,37-38]系列工作表明方形颗粒在容器中的沉降极易形成面对角线沿重力方向(边与水平面夹角45°)的团簇.这一特性可以通过平均场近似解释.力链穿过给定粒子的概率应与其侧面在水平方向上的相对投影成正比,方形颗粒在这一角度下力链的穿透概率取极大值,此时颗粒体系内部的沿重力方向的力链分布最接近高斯分布状态,颗粒间具有最大的接触面积.从侧视图可以看出,在圆筒边壁最初的几十转内,重力诱导颗粒迅速的掉落,容易形成由几个或者几十个颗粒组成的面对角线沿重力方向的团簇.后续边壁的往复旋转则是诱导这些团簇整体转动形成立方体颗粒某一面平行容器底面的团簇.文献[23]认为重力因素和边壁旋转因素对颗粒团簇的最终形态构成竞争关系.当旋转扰动强度足够剧烈时,团簇会以整体旋转的形式完成排列取向的转变.当旋转扰动强度较低时,体系最终为面对角线沿重力方向的颗粒团簇和某一面平行容器底面的颗粒团簇共存的状态,例如图4 内插图所示结构,此时 S4稳定在0.82 左右.

图4 γ 一定,不同峰值角速度 ω0 下,填充率 Φ 和有序度参量 S 4 的变化Fig.4 Volume fraction Φ and cubatic order parameter S4 versus number of rotation N for γ=1.01 and differentω0

2.3 立方体颗粒有序堆积的影响因素

Asencio 等[23]认为每次旋转时,对颗粒体系施加的 γ 对立方体颗粒的有序堆积起决定性的作用.如果 γ 大于0.5,那么立方体骰子必然能在容器约10 万次的往复旋转后达到有序堆积状态.此时每一层的立方体颗粒都排列成几乎完美的同心环.相反,如果 γ 低于0.5,那么有序堆积的速度就会变得非常缓慢,以至于很难判断颗粒是否最终能达到最密堆积状态.即使经过10 万次的旋转,靠近圆柱体中心的颗粒仍然处于高度混乱的状态.本文的模拟方案中,容器 γ 由 ω0和反转时间 Δt 决定.不同的 ω0和Δt可能对应相同的γ .因此设计了一组 γ 相同但 ω0不同的容器运动条件,考察立方体颗粒的有序堆积过程,如图4 所示.如果 γ 是立方体颗粒有序堆积的控制变量,那么可以预期只要 γ相同,尽管 ω0不同,容器各运动条件下颗粒有序堆积过程应该是几乎相同的.但是模拟结果显示 γ 一定时,随着 ω0的增大(相应的反转时间 Δt 增加),颗粒体系只需更少的往复旋转次数就可达到最密实状态并完成颗粒的有序排列.应当指出,ω0=2.50 rad/s的这组模拟,当往复旋转次数达到4000 次时仍未完成完全的有序化转变(有序度参数 S4约为0.82),这是因为靠近容器边壁的部分颗粒形成面对角线沿重力方向的团簇,如图4 内插图所示.无法确定更多的往复旋转次数是否一定能实现所有颗粒均为某一面平行水平面的有序排列.这种情况与文献[23]报道的低于0.5 时的旋转剪切结果类似,容器内两种取向的团簇颗粒共存.这意味着立方体颗粒通过边界的剪切作用完成有序堆积确实需要外界给予的扰动强度达到一定的值,但将作为衡量扰动强弱的指标并不完备,模拟结果显示这个强度指标与 ω0和Δt 有关.

为了进一步研究 ω0和 Δt 对立方体颗粒有序堆积过程的影响,首先设计了一组 ω0相同但 γ 不同的容器运动条件,模拟结果如图5 所示.ω0一定时,随着的 γ 增大,立方体颗粒需要更多的往复旋转次数才能达到最密实状态并完成颗粒的有序化转变.γ 对颗粒的密实化和有序化呈现消极影响,这一结果与文献[23]矛盾.同时设计了一组 Δt 相同但 ω0不同的运动方案,此时随ω0的增加 γ等比例增大,如图6 所示.结果显示更高的 γ 下立方体颗粒确实仅需要更少的往复旋转次数就可以完成颗粒的密实化和有序排列,这一结果与文献[23]一致.文献[23]并未给出转筒详细的工作条件,但提及到实验采用的转筒仅在反转时对颗粒有剪切作用.可以认为实验中容器的运动模式接近为方波形式,角速度反向所需要的时间可能为定值,如此 γ 的增大完全由峰值角速度的增大所导致,类似图6 结果所对应的运动方案.

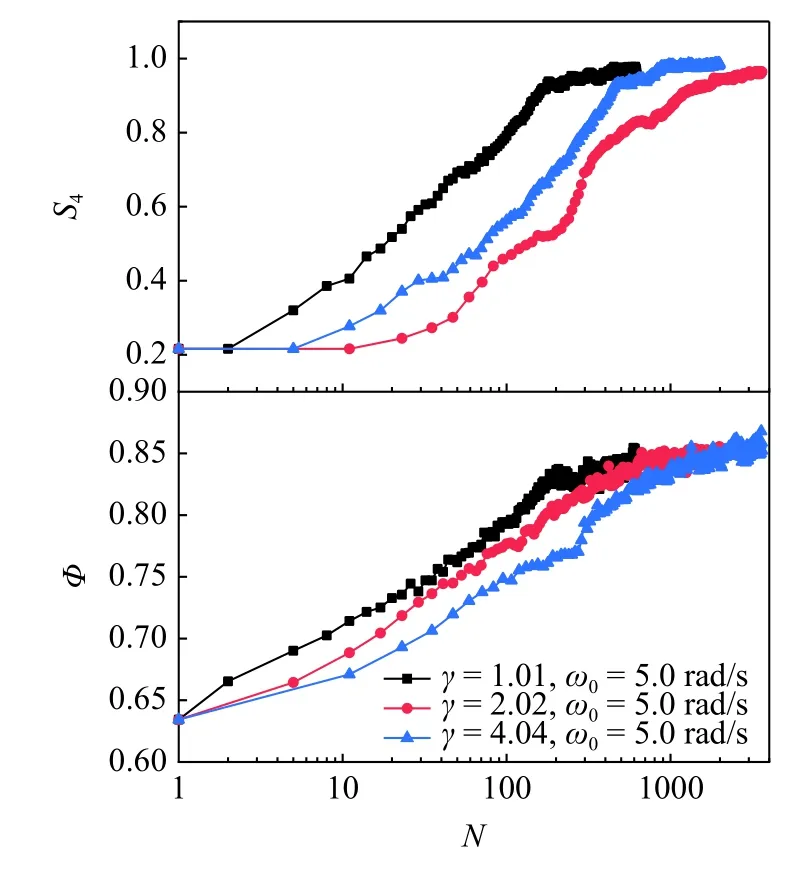
图5 角速度 ω0 一定,不同 γ 下,填充率 Φ 和有序度参量 S 4 的变化Fig.5 Volume fraction Φ and cubatic order parameter S4 versus number of rotation N for ω0=5.0 rad/s and differentγ

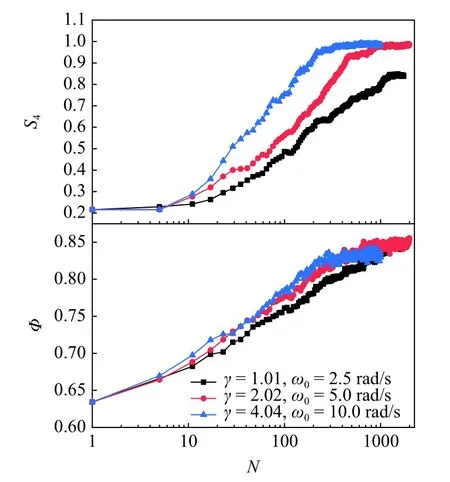
图6 反转时间一定,不同 γ 下,填充率 Φ 和有序度参量 S 4 的变化Fig.6 Volume fraction Φ and cubatic order parameter S4 versus number of rotation N for the constant inversion time and differentγ

综合以上结果,本文提出用容器的旋转角位移β作为衡量扰动强弱的指标更为合理.图7 给出了旋转角位移 β 和特征旋转次数 Nr的关系,图中所有模拟组的 S4最终的稳定值均大于0.94,可认为体系完成了有序堆积.对 β 与 Nr绘制双对数散点图并进行线性回归,得到 β 与 Nr之间的关系为

图7 特征旋转次数与旋转角位移的关系Fig.7 Characteristics rotation number versus angular displacement

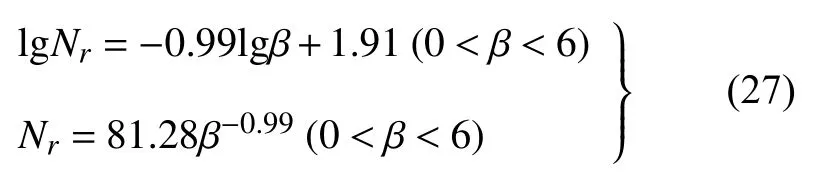
考虑到实验误差,可以认为 Nr和 β 之间为简单的反比例关系即

其中 Nr0为系数取决于颗粒体系的数量,容器能容纳的单层颗粒越多则 Nr0越大.利用这种反比例关系,很容易理解模拟中发现的S4曲线重合的现象.比如边界 γ=1.01,ω0=5 rad/s 和 γ=4.04,ω0=10 rad/s 的两个边界运动方案,对应的旋转角位移均为0.338 rad,因此两者的 Nr几乎完全相同,如图8 所示.

图8 相同 β 值下,填充率 Φ 和有序度参量 S 4 的变化曲线.Fig.8 Volume fraction Φ and cubatic order parameter S4 versus number of rotation N for the constantβ

这种反比例关系是因为,容器旋转扰动作为类似热涨落的驱动力,提供了立方体颗粒有序堆积的能量.考虑圆形底面的对称性,可以近似将所有颗粒受到的来自边界的摩擦力简化为对全体颗粒的力偶,单次旋转时边界对颗粒体系做功等于力偶矩乘以旋转角位移.旋转角位移越大,容器边界输入能量越多,颗粒越容易产生运动,直至完成有序排列,此时体系的势能最低,颗粒单元与相邻颗粒间的面-面接触约束最强烈.当然式(28)的适用范围一定存在上下限.对于适用上限可以合理想象即使旋转角位移非常大,但是完成有序堆积依然需要一定次数的往复旋转而不仅仅是一两次的旋转.对于适用下限上文已经阐述当旋转角位移小于某一临界值时,体系最终会形成两种形式的团簇颗粒共存的结构,只是下限的临界值所对应的力学机理有待进一步研究.

2.4 不同重力加速度下的立方体颗粒剪切排序

深空环境中,固体星球表面聚集着大量的颗粒物质.人类对于深空环境下颗粒物质的物理规律和操控方式的认知仍比较浅显.比如太阳系中大行星表面的风化层典型颗粒粒径小于小行星表面风化层的典型颗粒粒径,即使是这样简单的现象,人们对于其物理机制的认知尚未完全统一.深空环境的颗粒堆积问题亦是如此.为研究重力加速度对立方体颗粒受转动驱动实现有序堆积的影响,设计了三种不同重力加速度下(地球、火星和月球的重力加速度)的边界运动条件.鉴于颗粒物质具有非线性和对微小作用力敏感的特性,初始堆积状态将影响后续堆积演变特征,所以本文三种重力加速度下的颗粒堆积结构保持不变.且同时保持 γ=4.04,ω0=10 rad/s 不变,模拟结果如图9 所示.地球和火星的重力加速度下,立方体颗粒都实现了无序向有序的转变并达到了最密堆积和完全有序状态,但火星重力加速度下达到有序状态需要的往复旋转次数更多.而月球重力加速度下颗粒体系虽然 φ 和 S4也随着边界不断旋转而变大,但无法达到完全有序和最密实状态.上述结果表明,亚重力加速度条件下,容器的往复旋转依然是实现立方体颗粒有序堆积的有效方式,但重力加速度的减少会对立方体颗粒的有序堆积过程产生抑制效果.这是因为随着重力加速度的减小,颗粒间的摩擦力相应减小,不利于颗粒受到扰动后寻找下沉路径.本文也曾尝试过模拟十分之一地球重力加速度以及更低重力加速度条件下的立方体颗粒有序堆积过程,但上层颗粒极容易形成类似颗粒气体的漂浮状态,无法再将其视为一个类似固体的堆积体.

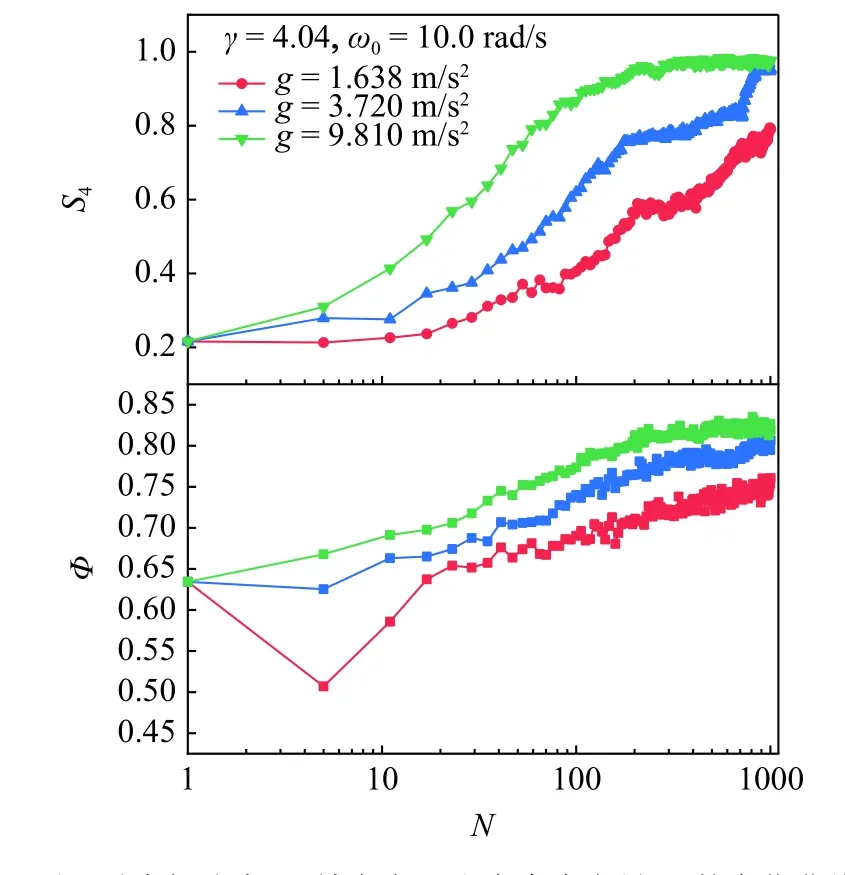
图9 不同重力加速度下,填充率 Φ 和有序度参量 S4 的变化曲线(模拟参数:边界 γ=4.04,峰值角速度 ω0=10.0 rad/s)Fig.9 Volume fraction Φ and order parameter S4 versus number of rotation N for different acceleration of gravity (γ=4.04,ω0=10.0 rad/s)

3 结论

基于超二次曲面方程构建立方体颗粒形态,采用离散元方法针对圆筒内随机堆积立方体颗粒在容器边界往复旋转作用下的有序化堆积行为开展数值模拟研究,复现了实验中观察到的立方体颗粒实现最密规则堆积的过程.通过本文研究,得到如下结论.

(1)立方体颗粒系统的体积分数和有序度随着容器往复旋转次数增加而逐渐增大直至稳定.颗粒系统的有序堆积过程表现为由外层颗粒向内部颗粒逐渐扩展的演化趋势.

(2)容器旋转角位移是立方体颗粒实现有序堆积过程的控制变量.颗粒完成有序堆积过程所需的特征旋转次数与容器旋转角位移呈现反比例关系.旋转角位移过低,体系只会形成某一面平行水平面的颗粒团簇与面对角线平行重力的颗粒团簇共存的结构.

(3)在亚重力环境下立方体颗粒同样可以通过容器的往复旋转实现最密规则堆积.重力加速度的减少会抑制立方体颗粒从无序堆积向有序堆积的转变.

致谢

本项目承蒙中国载人航天工程国际合作项目支持.