双自由面溶质-热毛细液层的不稳定性1)

赵诚卓 胡开鑫

(宁波大学机械工程与力学学院,浙江宁波 315211)

引言

Marangoni 对流是由于流体界面存在表面张力梯度而产生的流动[1-2].它主要存在于空间微重力环境或小尺度流动等表面张力占主导而重力效应较弱的情况中[3].其中表面张力梯度由表面温度不均导致的称为热毛细对流,由表面浓度不均导致的称为溶质毛细对流.在非等温双组分溶液中,液体表面往往同时存在温度梯度和浓度梯度,这种对流被称为溶质-热毛细对流[4-6].它广泛存在于晶体生长[7-8]、微流控[9-10]、合金浇筑凝固[11-12]、有机薄液膜的生长[13-15]等多种工业应用中,因而引起大量研究者的兴趣.

对溶质-热毛细对流的相关研究已有30 多年.Kanouff 和Greif[16]在研究焊接过程中铁熔体的热毛细流动时,发现氧化物和硫化物杂质会影响熔体的温度分布.Yasuhiro 等[11]、Arafune 和Hirata[12]对In-Ga-Sb 合金系统凝固过程中进行大量实验研究,证实了溶质毛细效应对热毛细效应具有重要影响.游仁然和胡文瑞[17]研究了浮区中热和溶质的毛细对流,发现浓度Marangoni 数对浮区中的流场和浓度场有明显的影响,对温度场的影响相对较小.Cröll等[6]通过对矩形液池内硅-锗(Si-Ge)熔体凝固过程中界面偏析引起的热-溶质毛细对流的实验研究发现:溶质毛细效应和热毛细效应会发生对抗作用.McTaggart[18]发现溶质毛细力和热毛细力的相互作用决定了双组分溶质-热毛细对流由稳态转向非稳态.Chen 和Su[19]发现由于热扩散和浓度扩散,在液层中会出现两种非稳态流动.

当表面张力梯度超过一定值时,Marangoni 对流会发生失稳.例如液层在交流电场不稳定性[20]、大尺寸液桥热毛细对流失稳[21]、旋转磁场中热质耦合对流不稳定性[22]等.近年来一些学者研究了溶质-热毛细对流的不稳定性.由于热毛细效应和溶质毛细效应的相互作用,不稳定性变得非常复杂[23].在晶体生长中,溶质毛细效应可以在溶质-热毛细流动不稳定性中发挥积极作用[24].文献[23-24]研究了双组分溶液的热-溶质毛细对流,发现流动失稳的自由表面会出现多种流场.陈捷超[25]研究了毛细力比对环形液池内耦合热-溶质对流的影响,发现随着毛细力比的增加,流动失稳的临界数会逐渐减小.

上述溶质-热毛细对流的研究主要针对单自由面液层.近年来Marangoni 对流的研究已拓展到双自由面液层.NASA 的Pettit[26]在国际空间站进行了一系列热毛细对流实验,结果表明双自由面热毛细液层能获得一种新的材料结晶过程.在工业应用中,溶质毛细效应和热毛细效应经常同时出现[4-6],因此非常有必要对双自由面液层溶质-热耦合的流动进行研究.在理论分析中,可以将单自由面液层的模型[27]拓展到双自由面液层.Yamamoto 等[28]对Pettit[26]的实验进行了数值模拟,发现液层的几何形状是导致振荡流动结构的关键因素.Hu 等[29]用线性稳定性分析方法研究了具有两个自由表面的热毛细液体层的失稳机理.上述实验、数值模拟和理论工作发现:双自由面液层与单自由面液层的Marangoni对流的失稳机制、扰动流场有显著的差别.

到目前为止还没有关于双自由面液层溶质-热毛细对流的研究,本文将研究此问题的不稳定性,在第1 节中给出了物理模型、无量纲控制方程;第2 节中用模态分析的方法先后研究了不同参数下的最优模态、扰动流场、能量分析和物理机制;第3 节总结了双自由面溶质-热毛细对流的失稳机制.

1 控制方程

考虑具有双自由面的液层,当液层厚度 2d 远小于液层流动的特征长度 L,例如 d=1 mm,L=20 mm[20],此时液层可近似看作无限大,如图1 所示.液面水平方向上的温度梯度(T1＞T2)和浓度梯度(C1＞C2)会导致表面张力梯度,进而驱动溶质-热毛细对流.其中 x,y 和 z 分别代表流向、展向和法向,d 为液层厚度的一半,τ13为表面剪切力.液面的表面张力为可近似的表达为温度 T 和浓度 C 线性函数[6,12,30]

图1 双自由面溶质-热毛细液层对流的示意图Fig.1 Schematic of the solutal-thermocapillary liquid layer with two free surfaces

其中 γT为表面张力温度系数,γC为表面张力浓度系数,.在流动模型中还考虑了Soret 效应,即温度梯度导致的浓度扩散;忽略Dufour 效应[31],即浓度梯度会导致热扩散.

设液层为不可压缩的牛顿流体,其无量纲控制方程组包括连续性方程(2)、动量方程(3)、能量方程(4)、传质方程(5)和本构方程(6)

其中 u,p,T,C 分别为速度、压强、温度和浓度,τ为应力张量,S 为应变率张量.在传质方程(5) 中表示Soret 效应.Reynolds 数 Re,Prandtl 数 Pr,Marangoni 数 Ma,Schmidt 数 S c,Soret 数 χ 分别定义为

其中 ρ 为流体密度,D 为溶质扩散系数,ξ 为热扩散率,ζ 为二元混合物的Soret 系数.

上自由面处(z=1)应力和速度的边界条件为

式中前两项方程表示溶质-热毛细效应,可由式(1)推得[25,30,32].第3 项表示自由面无变形.上自由面处的热平衡和Soret 效应分别表示为[25,30,32]

类似地,可以得到下自由面处(z=-1) 的边界条件

上述式中毕渥数 Bi=hd/k,其中 k,h 分别是导热系数、表面换热系数,在本文中,取 Bi=0 ;分别为液层上、下边界处气体温度.它们是强加给环境的热通量.这两项是为了能量平衡而引入的,可以由基本状态解来确定.

假设基本流为平行剪切流,得

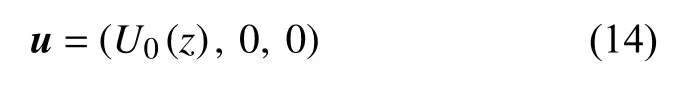
根据质量守恒,液层在同一垂直平面内通量为0,即

温度和浓度在 x 方向的分布是线性的,可得

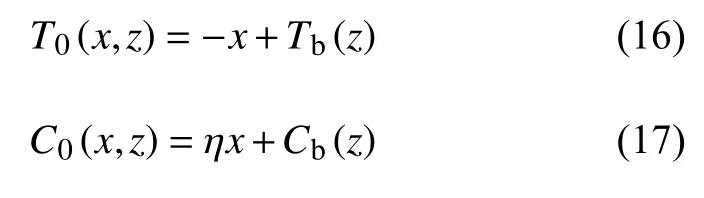
其中在具体实验中,可以在一个矩形方框的两对边分别施加热源和冷源,另外两对边为绝热层;同理,浓度梯度[12,26,28,35]也可以这样设置.设边界处的温度、浓度为

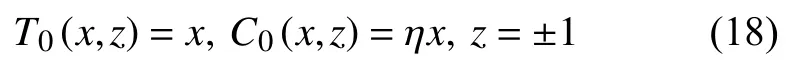
由上述条件可推出基本流的解

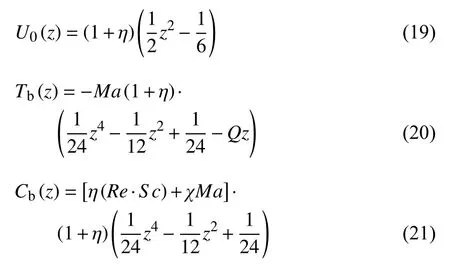
它们有如下关系式

以下采用模态方法分析液层的流动稳定性.在基本流场中叠加正则小扰动

式中带下标0 的变量表示基本流,无下标的变量表示扰动.式中 σ=σr+iσi为复频率,σr为增长率,ω=|σi|为角频率.α,β分别表示在x,y轴上的波数,总波数为k=,方向角本文中θ是以热毛细对流为基准.扰动方程和边界条件在附录A中给出.σ 可以通过Chebyshev 配点法求解,配置点数 Nc通常设置为70～ 100.

2 数值结果

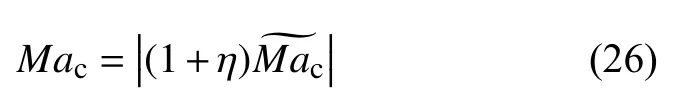
Mac越大表示稳定性更强.其中流动的参数估计如下所述,双组分溶(液的)Pr的范围是10-2～102,Sc的范围[6,30,32]是.Platten 等[36-37]对于Soret系数实验研究的评述,发现双组分有机溶液和水基溶液的Soret 系数在 [O(10-3)～O(10-4)]K-1.表1 为甲苯/正己烷混合溶液的物性参数[23].

表1 298.15 K 时甲苯/正己烷混合溶液(C0=26.17%)的物性参数Table 1 Physical properties of toluene/n-henxane mixture at T0=298.15 K and C0=26.17%

根据量级估计,取 0.01 ≤Pr ≤100,S c=100,χ=0.1.毛细比 η[7,16,38]通常情况下是负数,即溶质毛细力和热毛细力的方向相反.取 η=-0.5,-2 这两种情况进行计算,分别代表热毛细力大于和小于溶质毛细力但两者处于同一量级的情况,并且和纯热毛细对流(η=0)进行对比.

2.1 临界曲线

图2 画出了 η=0,-0.5,-2 在 0.01 ≤ Pr ≤100 下的临界曲线.其中UOW (upstream oblique waves),SSM (spanwise stationary mode),DSW (downstream streamwise wave),USW (upstream streamwise wave)分别表示为逆向斜波(90°＜θ ＜180°,σi＜0)、展向稳态模态(θ=90°,σi=0)、同向流向波(θ=0°,σi＜0)、逆向流向波(θ=180°,σi＜0).

对于纯热毛细流(η=0)的情况,图2(a)～图2(d)显示在 0.01 ≤Pr ≤111,Mac、波数k 和角频率ω 随Pr增加而增加.在 0.01 ≤Pr ≤1.1 时,临界模态是逆向斜波,θ 随 Pr的增加而增加;在1 .1 ≤Pr ≤111 时,临界模态是同向流向波.在 111 ≤Pr ≤200 时,临界模态是逆向流向波,Mac、波数 k 随 Pr 增加而略微增加,ω 随 Pr 增加而略微减小.

对于 η=-0.5 的情况,图2 显示 a2曲线对应0.01 ≤Pr ≤45.5,临界模态是展向稳态模态,随 Pr 的增加而增加,k=0.b2曲线对应 45.5 ≤Pr ≤62.4,临界模态是展向稳态模态,和 k 是随 Pr 增加而增加.c2曲线对应 62.4 ≤Pr ≤95,临界模态是同向流向波,Mac,ω,k 是随 Pr 的增加而增加.d2曲线对应95 ≤Pr ≤200,临界模态是逆向流向波,是随 Pr 的增加而减少,ω 和 k 随 Pr 的增加而增加.

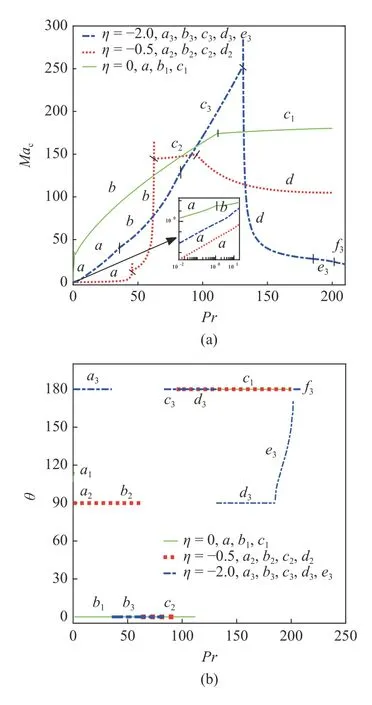
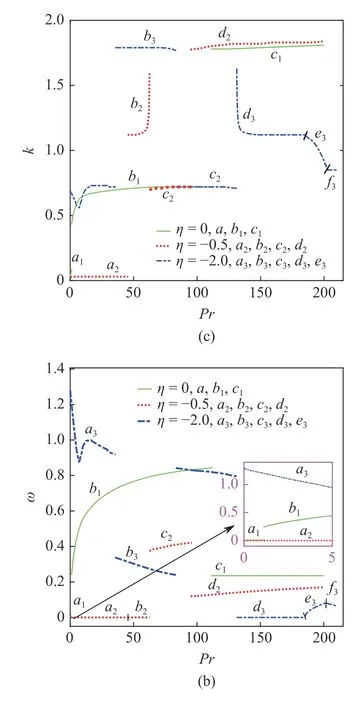
图2 临界参数随 Pr 的变化曲线:(a) Mac ;(b)波传播角 θ ;(c)波数 k ;(d)角频率 ω .曲线对应:UOW (a1,e3),SSM (a2,b2,d3),DSW (b3,b1,c2,c3),USW (a3,c3,d2,c1,f3)Fig.2 The variation of critical parameter with Pr .(a) Mac,(b) wave propagation angle θ,(c) wave number k and (d) angular frequency ω.The curves correspond to:UOW (a1,e3),SSM (a2,b2,d3),DSW (b3,b1,c2,c3),USW (a3,c3,d2,c1,f3)

对于 η=-2 情况,图2(b)显示了在0.01 ≤Pr ≤131区间内,Mac是随 Pr的增加而增加.a3曲线对应0.01 ≤Pr ≤35.6,临界模态是逆向流向波,0 .56 ≤k ≤0.73,0.87 ≤ω ≤1.28.b3曲线对应 35.6 ≤Pr ≤83.4,临界模态是同向流向波,k 和 ω 随 Pr 的增加而减少.c3曲线对应 83.4 ≤Pr ≤131,临界模态是逆向流向波,k=0.72,ω 随 Pr 的增加而减少.在1 31 ≤Pr≤210 区间内,Mac是随 Pr 的增加而减小.d3曲线对应1 31 ≤ Pr ≤185,临界模态是展向稳态模态,k 随 Pr 的增加而减少.e3曲线对应 185 ≤Pr ≤202,临界模态是逆向斜波,ω,θ随 Pr 的增加而增加,k 随 Pr 的增加而减少.f3曲线对应 202 ≤Pr ≤210,临界模态是逆向流向波,k=0.85,ω 随 Pr 的增加而减少.

2.2 扰动流场

本文画出了不同临界模态下的等温线图、等浓度线图和流线图,并以最大扰动温度为基准进行标准化.此时横轴方向为波的传播方向,其数值表示扰动相位 φ=αx+βy .

图3 和图4 分别显示了 η=-0.5,-2 的不同临界模态的扰动流场和浓度场.η=-0.5 的浓度场和温度场在同一模态下的分布是相似的,区别就是扰动的幅值大小不同.图3(a)、图3(c)的流场分别和纯热毛细对流(η=0)处于 a1,b1曲线段处模态的流场相似.图3(b)～图3(d)显示扰动场在同一周期内沿z=0呈反对称分布;图3(a)显示展向稳态模态模态的浓度场在 z 上无明显变化,流线显示在同一周期内4 个涡,扰动场在同一周期内沿 z=0 呈对称分布.图3(b)～图3(d)显示分别展向稳态模态、流向波、逆流向波模态的扰动流场在同一周期内呈反对称分布且有2 个涡.图3(b)的浓度幅值在表面附近和内部区域都有分布.图3(c)和图3(d)的扰动幅值只分布在内部区域.图4(a)显示 η=-2,Pr=1 的逆流向波模态的温度场和浓度场分布不相似,但是温度和浓度幅值均分布在表面区域.Pr=50,1 00 的扰动浓度场和扰动温度场分布是相似的.图4(a)～图4(c)的扰动场在同一周期内沿 z=0 呈反对称分布且有2 个涡,扰动浓度幅值分布在内部区域.图3(c)和图4(c)、图3(d)和图4(b)的波传播角、扰动流场的方向相反.

图3 η=-0.5 时临界模态的扰动流场.(a) SSM (Pr=0.01),(b) SSM (Pr=50),(c) DSW (Pr=70),(d) USW (Pr=100)Fig.3 The perturbation flow field of the different preferred modes at η=-0.5.(a) SSM (Pr=30),(b) SSM (Pr=0.01),(c) DSW(Pr=70),(d) USW (Pr=100)

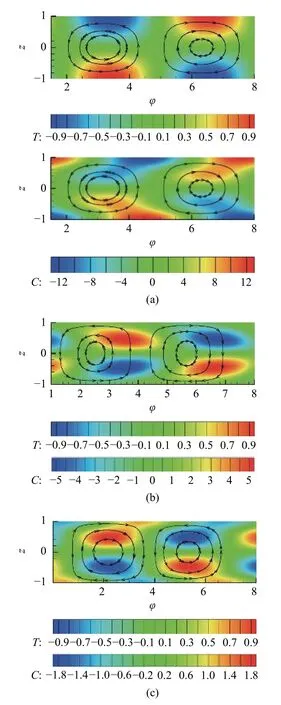
图4 η=-2 时不同临界模态所对应的扰动流场.(a) USW (Pr=1),(b) DSW (Pr=50),(c) USW (Pr=100)Fig.4 The perturbation flow field of the different preferred modes at η=-2.(a) DSW (Pr=1),(b) USW (Pr=50),(c) DSW (Pr=100)

2.3 能量分析

扰动动能的变化率可以写成如下形式[39]

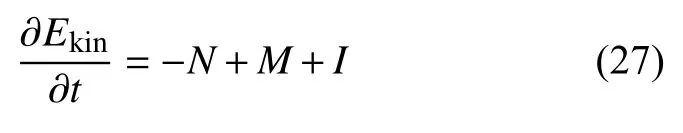
其中 N 为扰动应力做的功,N ＞0 代表耗散;M 为表面毛细做功,I 为扰动流与基本流之间的相互作用.N,M,I具体为

为了进一步研究热毛细效应和溶质毛细效应对做功的影响,可以把 M 写成式(29)的形式,其中 MT,MC分别为热、溶质毛细力做功.式(29)中分别为热、溶质毛细力

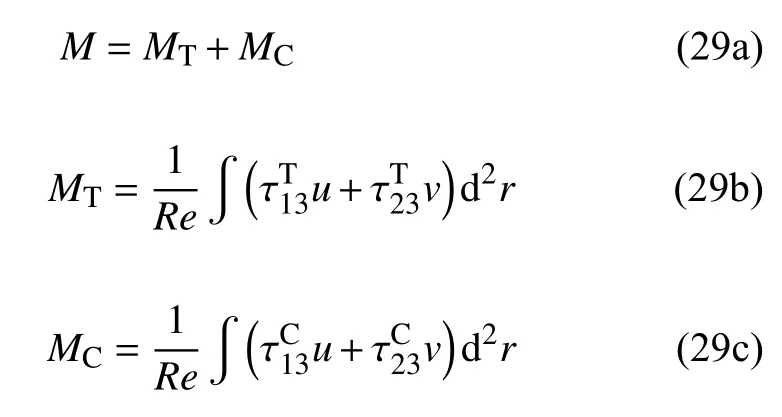
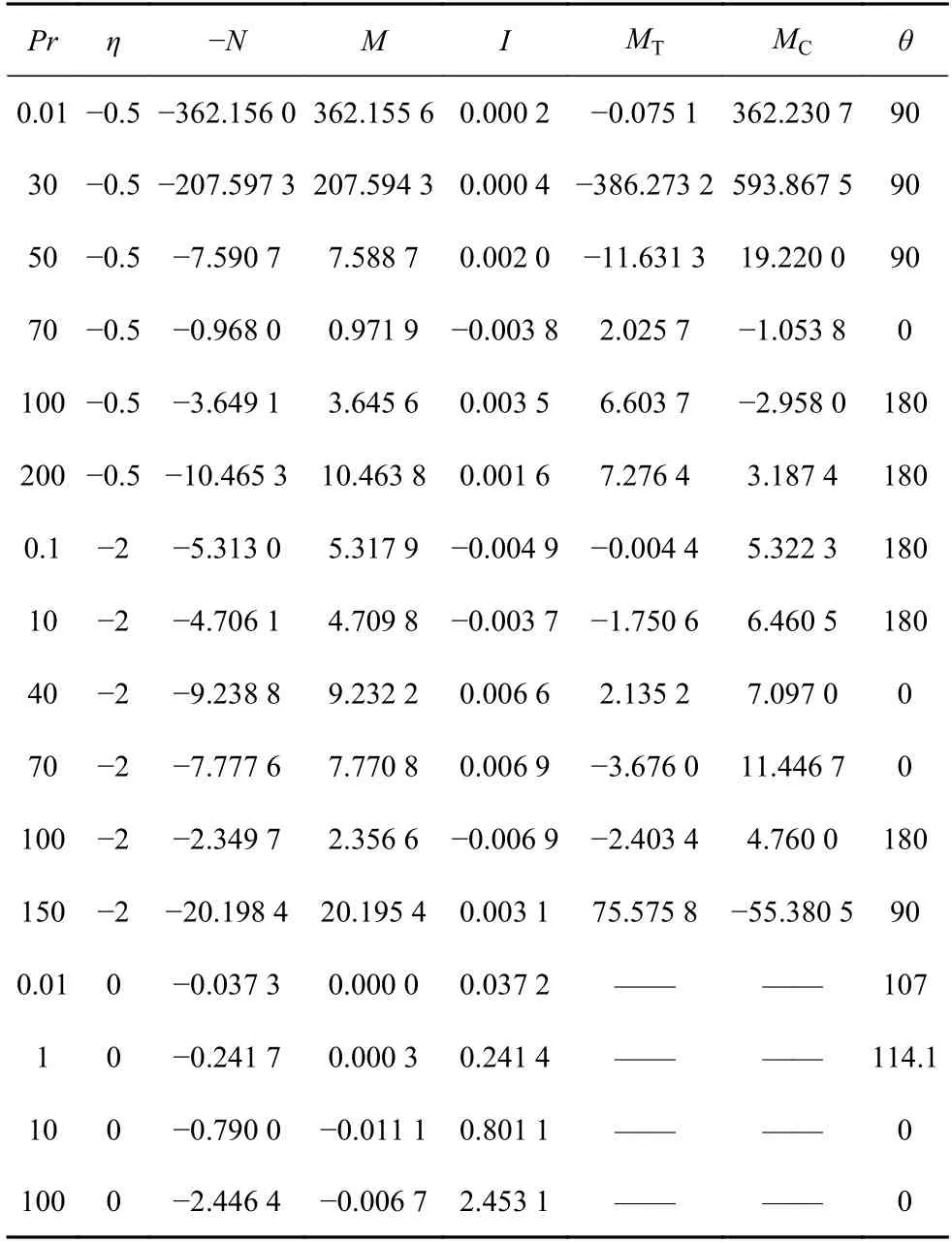
表2 不同参数下各扰动能量变化项的值Table 2 Values of perturbation energy variation terms at different parameters.

结合图1(b),从表2 中可以看出,扰动能量的来源是表面张力做功,扰动流与基本流的相互作用可以忽略.

在 η=-0.5 情况下:(1)曲线 a2,b2对应展向稳态模态,MT＜0,MC＞0,溶质毛细力做功占比随 Pr 增加而减少,热毛细力做功占比随 Pr 增加而增加,并且在 Pr 较小的情况,热毛细力做功可以忽略;(2)c2是顺向流向波,MT＞0,MC＜0 .(3) d2段是逆向流向波,MT＞0,MC随着 Pr 的增加由负变正.

在 η=-2 情况下:(1) a3段为逆向流向波,MT＜0,MC＞0.(2) b3段为同向流向波,MC＞0,MT是随Pr增加而减少,MT随 Pr 增加由正变负.(3) c3段为逆向流向波,MT＜0,MC＞0.(4) d3,e3,f3分别为展向稳态模态、逆向斜波、逆向流向波,MT＞0,MC＜0.

2.4 讨论

在小 Pr 数情况下,图3(a),图3(b)和图4(a)显示,扰动的幅值分布在自由面是由于对流导致的;扰动温度的幅值小于扰动浓度的幅值,能量分析显示表面溶质毛细力做功大于热毛细力做功,热毛细力和溶质毛细力相互对抗.

在大 Pr 数情况下,图3(c),图3(d)和图4(b),图4(c)扰动幅值分布在中间区域是由于对流(U0T,U0C)和垂直对流自由面的扰动是由于热扩散和浓度扩散导致的.在 η=-2 且小 Pr 数情况下,扰动温度场和扰动浓度场分布不同的也是由热扩散和浓度扩散导致的.

3 结论

本文采用线性稳定性分析方法研究了不同毛细比下的溶质-热毛细对流随Pr 变化的对流不稳定性,并结合流场图和能量分析,发现以下结论:

(1)溶质-热毛细对流的临界模态相比于纯热毛细对流有较大的差别.前者分为同向流向波、逆向流向波、展向稳态模态、逆向斜波;而后者分为逆向斜波和同向流向波;

(2) Pr 和 η 对流动稳定性的影响并不是单调的.在中小 Pr 数下,Pr 数的增加会使 Mac增加;在大Pr数下,Pr 数的增加使 Mac减小.在较大 Pr 情况中,η的减小会使 Mac减小;在其他参数中,η 的变化会使Mac发生多种变化;

(3) 不同临界模态的扰动场在同一周期沿着z=0的水平面呈反对称分布或对称分布.在η=-2且 Pr 较小时,扰动温度场和扰动浓度场分布不相似;在其他参数下,扰动温度场和扰动浓度场分布都是相似的;

(4)表面毛细力做功为流动主要能量来源,扰动流与基本流的相互作用可以忽略不计.在 η=-0.5 情况下,当 Pr 较大时,热毛细力做功和溶质热毛细力共同做正功;在其他参数下,热毛细力做功和溶质热毛细力做功符号相反.在 η=-2 时,溶质毛细力做和热毛细力做功符号相反.

附录

将式(24)代入控制方程、本构方程和边界条件中,可得线性扰动方程

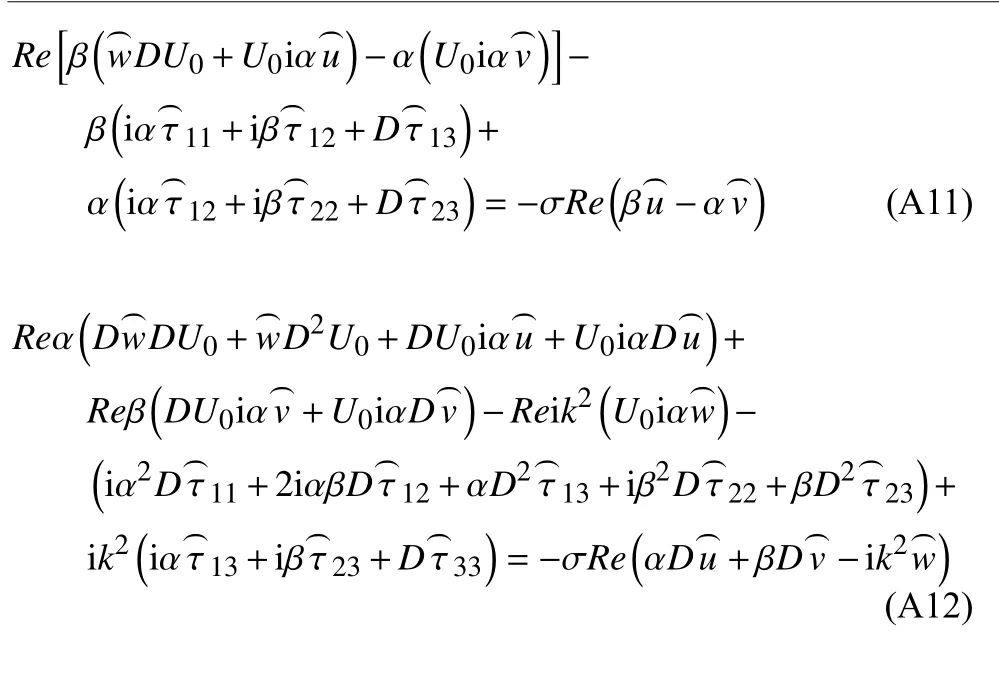
在 z 方向用Gauss-Lobatto 配点进行离散.在流场内部设置为;边界处() 设置2 个配点.变量用级数展开,例如i=1,2,···,Ncz=±1

最终式(A1),式(A5)～ (A12)可以写成 W g=σZ g 的形式.其中 W,Z 都为 (11Nc+8) 阶方阵,其中广义特征值 σ 和广义特征值向量 g 可以通过Matlab 中的QZ 算法算出.