考虑位错密度和损伤的NiCoCrFe高熵合金晶体塑性有限元分析

胡 广，赵英杰，马胜国，张团卫，赵 聃*，王志华

(1 太原理工大学 机械与运载工程学院 应用力学研究所，太原 030024；2 材料强度与结构冲击山西省重点实验室，太原 030024；3 太原理工大学 力学国家级实验教学示范中心，太原 030024)

高熵合金(high entropy alloys, HEAs)也被称为成分复杂合金(compositionally complex alloys)或多主元合金(multi-principal element alloys)，其概念在2004年被首次提出[1]。研究发现，不同于对传统材料的认知，HEAs的高混合熵增强了固溶体的相稳定性，并促进合金形成简单固溶体[2-3]。HEAs具有很多优异的性能：高强度[4]、高塑性[5]、良好的耐磨性和抗腐蚀性[6-7]以及优越的高低温性能[8-9]。众多学者对其微观结构演化机理进行了广泛研究。Zhang等[10]研究了NiCoCrFe静态载荷和动态载荷下的力学响应，发现NiCoCrFe在动态载荷下的强度和塑性得到提升，其原因在于短程有序/团簇(short-range orders/clusters)和纳米孪晶对位错运动的作用。针对NiCoCrFe在室温(293 K)和液氮温度(77 K)下的变形响应，Wang等[11]采用原位中子衍射方法测定层错和位错密度的演化，结果证实低温条件下位错密度和纳米孪晶的增加使合金强度和塑性均得到提升。

晶体塑性有限元(crystal plasticity finite element method，CPFEM)作为一种联系晶体材料宏观力学行为和微观结构演化的研究方法，通过考虑晶体位错滑移、孪晶以及相变等多种物理机制来描述晶体材料的塑性变形、硬化行为及各向异性[12-14]。Knezevic等[15]在基于位错密度的CPFEM模型中引入了应变率和温度敏感参数，并使用一套模型参数精确地描述了钴基高温合金Haynes 25在不同应变率下的力学响应和织构演化。Ardeljan等[16]基于多滑移位错理论提出一种描述多晶聚集体各向异性、应变速率效应以及温度敏感性的多尺度模型，并使用此模型研究了Zr/Nb两相层状复合材料在大塑性变形下的织构演化和微观机制。此外，一些基于位错密度的CPFEM模型还考虑孪生等机制的影响[17-18]。Gao等[19]在CPFEM模型中同时考虑位错热激活机制、位错密度以及孪晶机制，实现对不同应变率条件下NiCoCrFe力学响应、孪晶以及位错密度等演化的预测。

有限变形过程中金属的损伤行为也是实验以及理论研究所关注的一个热点。连续介质损伤与晶体塑性理论的有效结合可以准确预测多晶金属材料的损伤行为(如颈缩等现象)。在连续介质损伤理论框架下，Kim等[20]分别将4种损伤模型耦合到CPFEM中，并对比分析不同模型对AA6002-T4损伤演化行为的预测结果，研究表明考虑损伤的晶体塑性模型能够合理地预测颈缩行为和颈缩方向。Lv等[21]将最大剪应变损伤模型与传统硬化模型结合，预测了NiCoCrFe拉-剪复杂应力下的损伤行为和织构演化，预测结果与实验吻合良好。本工作从宏观和微观尺度出发，发展考虑位错密度和连续介质损伤的跨尺度晶体塑性模型，并采用CPFEM与实验相结合的方式，研究NiCoCrFe的宏观和微观力学响应，探讨NiCoCrFe损伤行为以及微观结构的演化规律。

1 实验材料与方法

1.1 实验流程

在高纯氩气环境下通过真空熔炼炉制备NiCoCrFe，原料Co，Cr，Fe，Ni纯度均为99.9%。为确保成分均匀，合金铸锭反复熔炼5～6次，然后将铸锭吸铸成100 mm×22 mm×2 mm的板材。通过轧制和退火来消除板材制备过程中引入的孔洞和缺陷，其中轧制量控制在55%，轧制后板材厚度约为0.9 mm。退火温度控制在900 ℃，时长为1 h，随后进行水淬冷却。

采用电火花切割方法沿板材轧制方向制备准静态拉伸试样。图1为拉伸试件标距段尺寸及三维宏观多晶模型示意图。图1(a)为准静态拉伸试件标距段尺寸，其长(L)、宽(W)分别为10 mm和2 mm。在实验前使用砂纸打磨拉伸试件以消除表面缺陷。在室温条件下，使用高铁试验机对NiCoCrFe试件进行准静态拉伸，应变率控制在10-3s-1，为保证实验的有效性，拉伸实验至少重复3次。

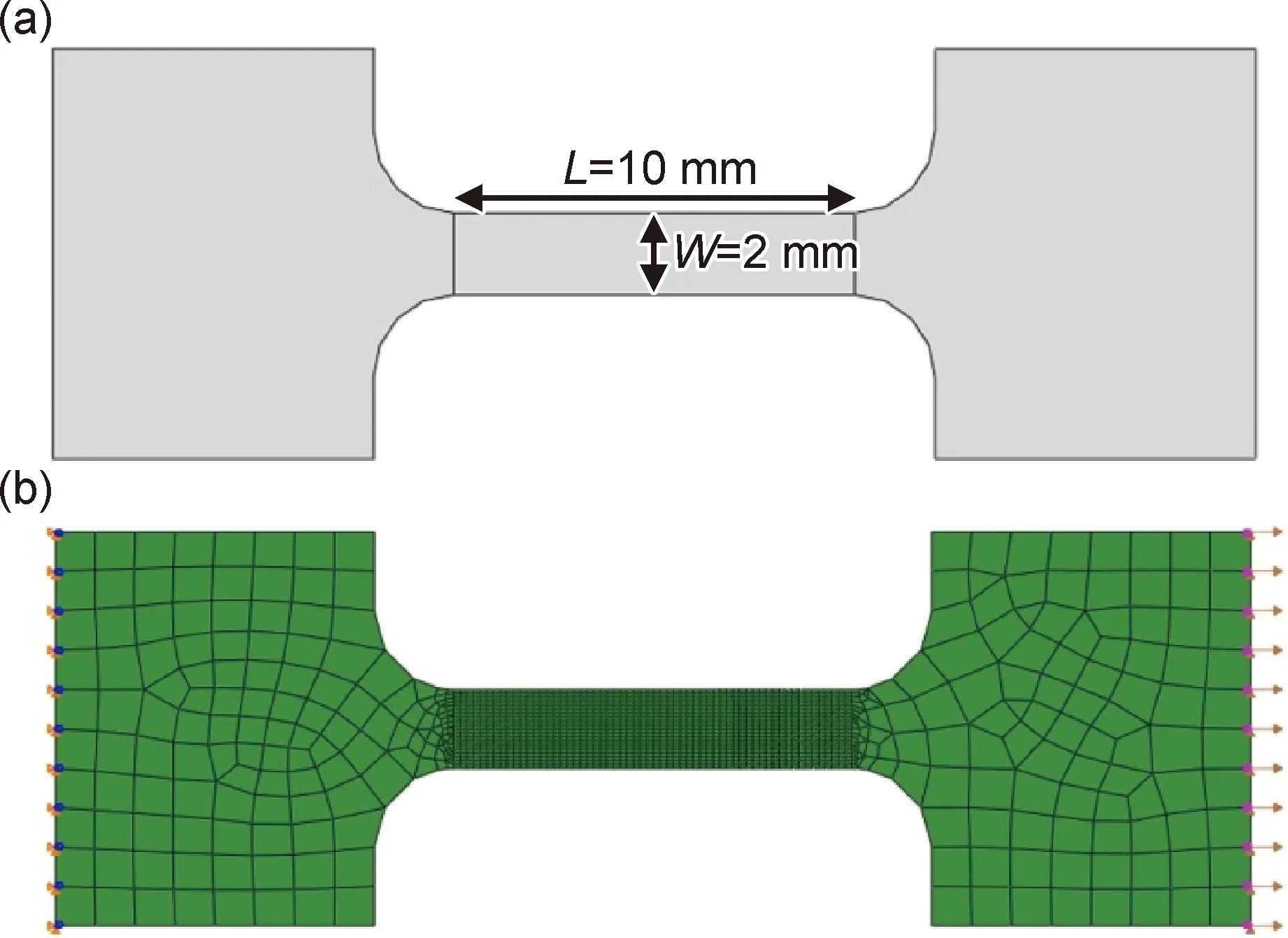
图1 实验试件标距段尺寸(a)和划分网格后的三维宏观多晶模型及边界条件(b)Fig.1 Dimension of the test specimen(a) and 3D macro polycrystalline model after meshing and boundary conditions(b)

在EBSD表征前，使用不同颗粒度砂纸对变形前后试件标距段进行打磨抛光，然后使用体积比9∶1的乙醇和高氯酸溶液进行电解抛光，直流电压15 V，持续时间20 s。采用热场发射扫描电子显微镜(JEOL JSM-7100F)安装的EBSD探针(HKL NordlysNano)检测未变形和变形试样的微观组织和织构情况。表征测试在加速电压为20 kV的条件下进行，扫描步长为0.5 μm，并采用HKL Channel 5软件包对EBSD数据结果进行分析处理。

1.2 晶体塑性理论

基于连续介质力学对有限变形的描述，通过变形梯度联系当前构型x和初始构型X，即dx=FdX。变形梯度F一般被分解为:

F=Fe·Fp

(1)

式中：Fe为弹性变形梯度；Fp为塑性变形梯度。塑性变形梯度考虑了不可恢复的位错滑移变形，而弹性变形梯度则考虑了晶格的可恢复变形和重取向。

考虑位错滑移为晶体变形的微观机制，塑性速度梯度Lp可以表示为：

(2)

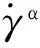
综合考虑数值分析的准确性和收敛性[20-21]，本工作损伤演化选用CDM框架下的滑移系最大剪应变模型，该模型能够在微观尺度下有效捕获NiCoCrFe各个滑移系损伤的演化情况，其形式如下：

(3)

式中：γm为最大剪切应变，即FCC金属变形过程中12个滑移系中剪切应变的最大值；D为损伤因子；Dmax为损伤最大值；γini与γmax分别为损伤初始时的最大剪切应变和损伤演化至最大值时的最大剪切应变。当滑移系最大剪切应变γm超过γini时，损伤在该滑移系开始演化。当γm超过γmax时，该滑移系损伤停止演化并保持最大值；M为损伤曲线形状系数。

采用现象学本构模型[22]描述晶体的变形行为，该本构模型是针对FCC金属体系的幂率形式流动准则[13,23]，引入损伤因子后可表示为：

(4)

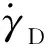
假设每个滑移面上位错运动的阻力来源于摩擦应力、固溶强化、晶界障碍以及运动位错与林位错的交互作用，其表达式如下：

(5)

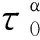
林位错强化模型认为，金属材料变形过程中林位错阻碍了位错的运动近而实现应变强化。本工作采用考虑滑移系交互矩阵Gαβ的林位错强化模型[24]，其可以表示为：

(6)

式中：μ为剪切模量；ρ为滑移系的林位错密度；b为柏氏矢量；Gα β为滑移系交互矩阵，对于FCC金属材料Gα β是一个12×12的矩阵[24]，只包含6个独立参数G0～G5，其值分别为0.1，0.22，0.3，0.38，0.16和0.45。

位错密度的演化采用单变量位错密度模型(K-M模型)[25]，该模型以总位错密度作为内部状态变量(internal state variables，ISVs)，并假设位错密度均匀分布，其表达方式如下：

(7)

式中：k1和k2分别为位错的增殖系数和湮灭系数。

2 结果与分析

2.1 NiCoCrFe多晶模型宏观损伤和织构演化分析

图1(b)为用于模拟单向拉伸加载的三维宏观多晶计算模型，其中每一个网格代表一个晶粒，网格类型选六面体8节点线性减缩积分单元(C3D8R)，并使用Python程序包将退火后NiCoCrFe欧拉角等取向信息赋给多晶模型作为CPFEM模拟的初始织构。

图2，3分别为NiCoCrFe合金的EBSD反极图(inverse pole figure,IPF)和极图。退火后NiCoCrFe EBSD反极图如图2(a)所示，900 ℃退火1 h后部分晶粒尚未完全再结晶，且退火后的NiCoCrFe表现为随机织构。图2(b)和图3(b)为试件准静态拉伸变形后EBSD反极图和极图(RD为轧制方向和拉伸方向)。与退火后的晶粒形貌和随机织构不同，经准静态拉伸变形后的晶粒沿RD方向延伸，晶粒表现为(111)∥RD，(100)∥RD的择优取向。根据文献可知[10]，FCC金属在经历大塑性变形后晶粒会发生旋转，进而形成典型的强(111)∥RD织构。使用JTEX软件处理CPFEM模拟NiCoCrFe拉伸变形后的织构。NiCoCrFe准静态拉伸变形中仅有少量的孪晶生成[10]，其对织构演化影响较小，因此本工作通过CPFEM分析织构演化时并未考虑孪晶的影响。图3(c)为CPFEM模拟三维宏观多晶模型拉伸变形后的极图。CPFEM模拟准静态拉伸过程中，晶粒取向会随着变形的增加而发生变化。当颈缩现象发生后，颈缩区域附近晶粒沿RD方向表现为强(111)∥RD织构和较弱的(100)∥RD织构，这与实验织构演化趋势大致相同。由于CPFEM模拟中各晶粒之间的约束限制和实际情况有所差异，导致模拟的织构结果比实验分散且强度偏低。

图2 NiCoCrFe合金EBSD反极图 (a)退火后；(b)变形后Fig.2 EBSD-IPF of NiCoCrFe alloy (a)after annealing;(b)after deformation

图3 NiCoCrFe合金极图 (a)退火后；(b)拉伸实验后；(c)CPFEM拉伸模拟Fig.3 Polar diagrams of NiCoCrFe alloy(a)after annealing;(b)after tensile test;(c)CPFEM tensile simulation

图4为NiCoCrFe拉伸实验和CPFEM模拟结果。图4(a)为准静态拉伸实验和CPFEM模拟获得的工程应力-应变曲线，图a1，a2分别为NiCoCrFe拉伸实验和模拟颈缩区域的形状和尺寸。NiCoCrFe晶体塑性模型相关参数见表1。根据工程应力-应变曲线可知，曲线可分为3部分：弹性变形和初始屈服阶段(Ⅰ)，应变强化阶段(Ⅱ)和损伤软化阶段(Ⅲ)，其中NiCoCrFe屈服强度约为300 MPa，极限拉伸强度为650 MPa，在工程应变32.5%附近发生损伤软化现象直至断裂。考虑损伤的CPFEM模型准确地描述材料拉伸过程中由Ⅱ阶段向Ⅲ阶段的过渡现象，未加损伤的CPFEM模型仅能较好地描述Ⅱ阶段的力学响应，而Ⅲ阶段存在较大的偏差。同时，使用考虑损伤的CPFEM模型预测颈缩区域的变形形状和尺寸，实验获得的颈缩区域长度比CPFEM预测结果小7%，CPFEM预测的颈缩区域宽度比实验结果大23%。实验观测的颈缩区形貌和模拟结果的差异主要由两方面引起：1)相关测量误差。本工作采用多次测量取平均值的方法，尽可能消除断裂后试件颈缩区域由于断面变形不均匀所带来的测量误差。2)CPFEM计算过程中并未对达到最大损伤的网格单元进行删除。同时，由式(4)可知，损伤因子D的演化范围为0～1，而当D取值接近1时(即完全损伤状态)会造成数值计算收敛困难。因此，综合考虑计算的准确性和收敛性，将损伤因子D的最大值设置为0.8。当D演化至0.8时，单元并未完全损伤，仍会保留部分应力，导致模拟过程中颈缩区域刚度较大，与真实颈缩区域形状和尺寸相比会有误差。参考Kim等[20]通过CPFEM对AA6022-T4拉伸后颈缩区域的预测(模拟与实验误差约为24%)，本工作对NiCoCrFe颈缩区域整体形貌演化趋势的模拟结果也是合理的。

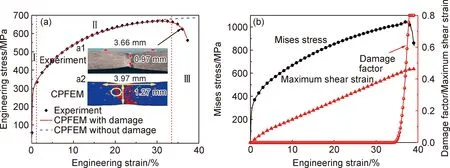
图4 CPFEM模型中工程应力-应变曲线，颈缩区域形状和尺寸对比(a)，CPFEM模拟颈缩区域损伤晶粒(图4(a2)中黄色圆形区域)Mises应力，损伤因子以及滑移系最大剪切应变演化曲线(b)Fig.4 Engineering stress-strain curves in the CPFEM model and the size and shape comparison of the necking region(a),CPFEM simulates evolution curves of Mises stress,damage factor and slip system maximum shear strain of damaged grains (yellow circular region in fig.4(a2)) in the necking region(b)

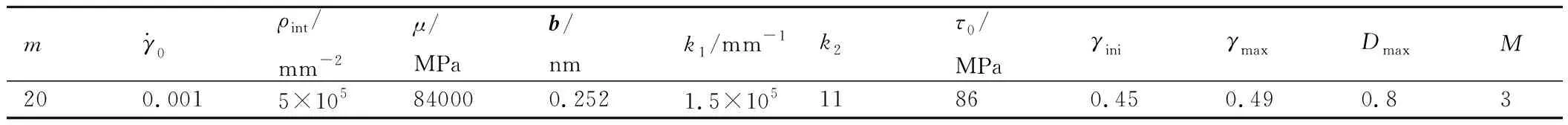
表1 NiCoCrFe晶体塑性模型相关参数Table 1 Relative parameters of crystal plasticity model of NiCoCrFe

图4(b)为CPFEM模拟颈缩区域损伤晶粒(图4(a2)黄色圆形区域)的应力状态和损伤演化情况。由于当前模型损伤基本变量选用的是滑移系最大剪应变，因此晶粒变形过程中剪切应变最大的滑移系为潜在的损伤初始位置。该晶粒在工程应变35%处滑移系最大剪切应变达到损伤模型应变临界值0.45，损伤开始演化。随着损伤的累积，由于损伤软化的作用该晶粒承受的应力开始下降。随着应变的增大，当多数晶粒发生损伤时，三维宏观多晶模型的力学响应逐渐由应变强化阶段向损伤软化阶段过渡。

需要注意的是，初始位错密度ρint的单位均为mm-2，并且考虑到CPFEM数值模拟的收敛性，将损伤最大值Dmax和损伤曲线形状系数M分别设为0.8和3[20]。

图5为工程应变35%时三维宏观多晶模型标距段的Mises应力、对数应变、位错密度和损伤分布云图。分析可知，此时三维宏观多晶模型的力学响应处于损伤软化阶段，并且发生了明显的应变局部化。对数应变集中区域与损伤分布大致相同，说明应变局部化与损伤演化有较强的关联。实际上，大多数延性金属变形到一定程度后都可能会发生应变局部化现象[26]，这主要是材料经历大变形后受力和变形不均匀造成的。材料内部微孔洞和微裂纹(本文中为损伤)的形成和扩展促进了局部的不均匀变形，导致局部剪切化开始(即颈缩)，直至材料断裂失稳。此外，由于晶粒损伤软化的作用导致颈缩区域损伤晶粒所承受的应力向未损伤晶粒传递，表现为损伤晶粒应力下降而未损伤晶粒应力上升。颈缩区域位错密度明显大于非颈缩区域且分布不均匀，其原因可能是应力传递使颈缩区域未损伤晶粒承受了更剧烈的位错滑移变形，并且各个晶粒间存在较大的取向差，进而造成位错在损伤晶粒与未损伤晶粒晶界处发生塞积。

图5 CPFEM模拟工程应变35%时Mises应力(a),对数应变(b),位错密度(c)以及损伤(d)分布云图(试样标距段)Fig.5 CPFEM simulated Mises stress(a),logarithmic strain(b),dislocation density(c) and damage(d) distribution contours at 35% engineering strain(sample gauge length)

2.2 NiCoCrFe微观结构损伤分析

图6为所建立的NiCoCrFe三维微观多晶模型。为了研究微观尺度下NiCoCrFe多晶体损伤的形成以及演化规律，该模型共包含了81个不同取向和形貌的晶粒，其尺寸为50 μm×20 μm×2 μm。模型仍采用六面体8节点线性减缩积分单元(C3D8R)，并对模型施加单轴加载，应变率控制在10-3s-1。为了降低单元网格数目对应力-应变场模拟结果的影响，该模型共划分64000个网格单元，以确保较为真实反映晶界和晶粒形貌。

图6 三维微观多晶模型及施加的边界条件Fig.6 3D micro polycrystalline model and applied boundary conditions

图7为三维微观多晶模型Mises应力、位错密度、最大剪切应变以及损伤分布云图。如图7(a)，(b)所示，三维微观多晶模型拉伸过程中应力和位错密度呈不均匀分布，在B1～B3，A1～A4区域晶粒晶界处发生了明显的应力集中和位错塞积现象。造成应力和位错密度分布不均匀的原因，可能是由于不同晶粒间取向的差异。多晶模型变形过程中，一些软取向晶粒容易发生塑性变形，并在晶粒内部产生大量的位错，当位错运动至相邻硬取向晶粒晶界处时受到阻碍，导致晶界附近位错密度增加，进而形成应力集中[27]。由图7(c)，(d)以及式(3)可知，损伤的演化依赖于滑移系最大剪切应变，而最大剪切应变主要受晶粒大小、形貌以及取向影响，其分布决定着损伤的初始演化位置和生长趋势。工程应变为37%时，滑移系最大剪切应变主要集中在三叉晶界处，与损伤的分布、应力以及位错密度集中区域大致相同。

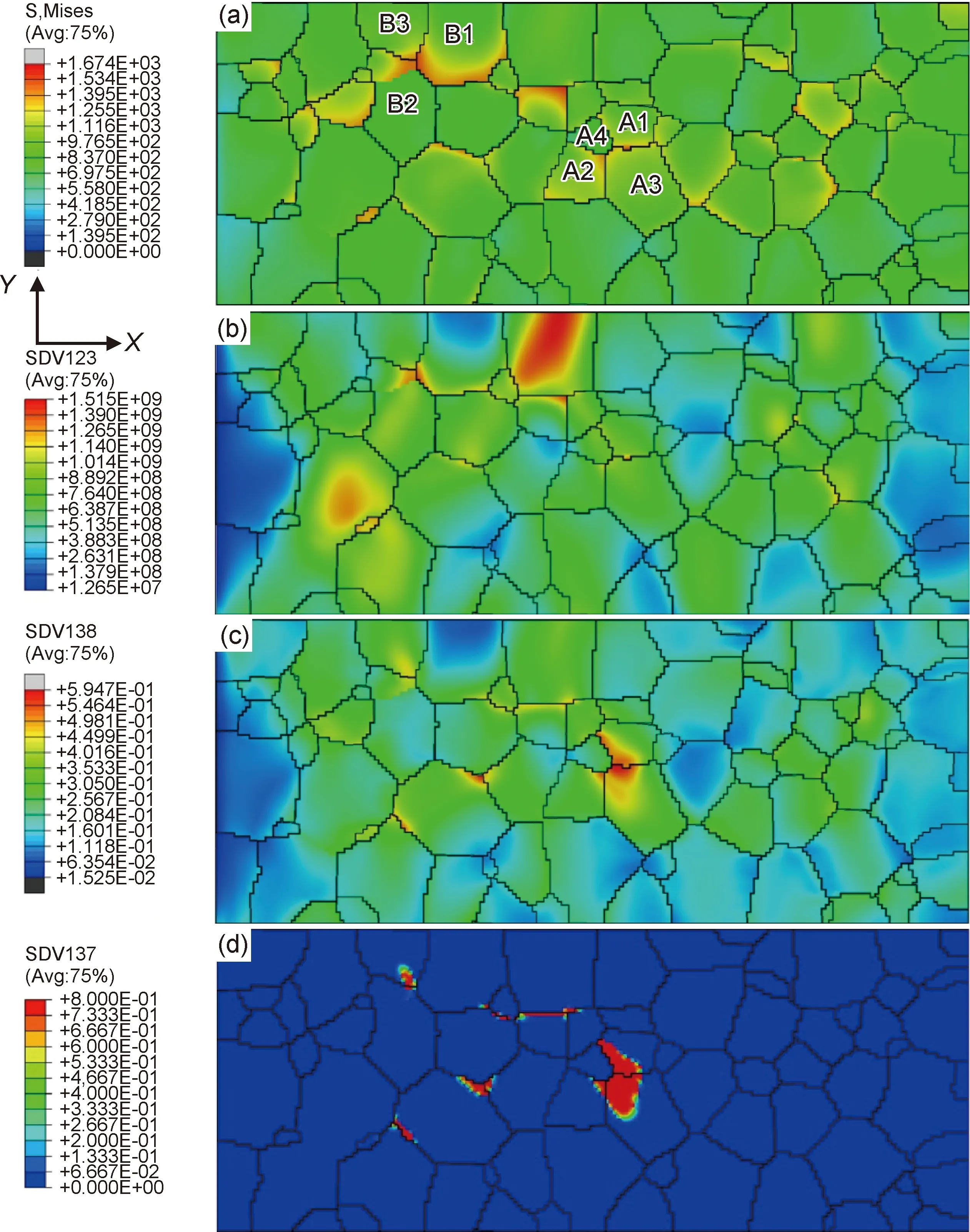
图7 工程应变30%时Mises应力(a)和位错密度(b)分布云图，工程应变37%时最大剪切应变(c)和损伤(d)分布云图Fig.7 Mises stress(a) and dislocation density(b) distribution contours at 30% engineering strain, maximum shear strain(c) and damage(d) distribution contours at 37% engineering strain

图8为A1～A4区域晶粒晶界附近的Mises应力演化曲线及损伤分布云图。结合图4(a)和图8分析可知，CPFEM预测的微观多晶模型损伤形成于应变强化阶段后期，并且在损伤软化阶段生长扩展，损伤的形成机制表现为晶间损伤，即损伤形成于晶界处。如图8所示，微观多晶模型初始损伤点(initial damage point)在工程应变32%处开始演化，此时损伤软化效应并不明显，微观多晶模型的力学响应仍处于应变强化阶段。工程应变为35%时，损伤由晶界初始损伤点处向A1和A3晶粒内部生长，分析晶界处初始损伤点附近点1和点2可知，点1和点2的损伤软化行为相较于初始损伤点有明显的滞后，并且随着变形的增加，两点的Mises应力明显上升。其原因在于，当晶界处某点开始发生损伤时，损伤点的软化效应会影响其周围的区域，使其承受更大的应力，并促进该区域损伤的生长。随着工程应变的继续增大，损伤已在多处晶界位置演化，并且向晶界附近的晶粒内部快速扩展，直至材料发生失稳破坏。

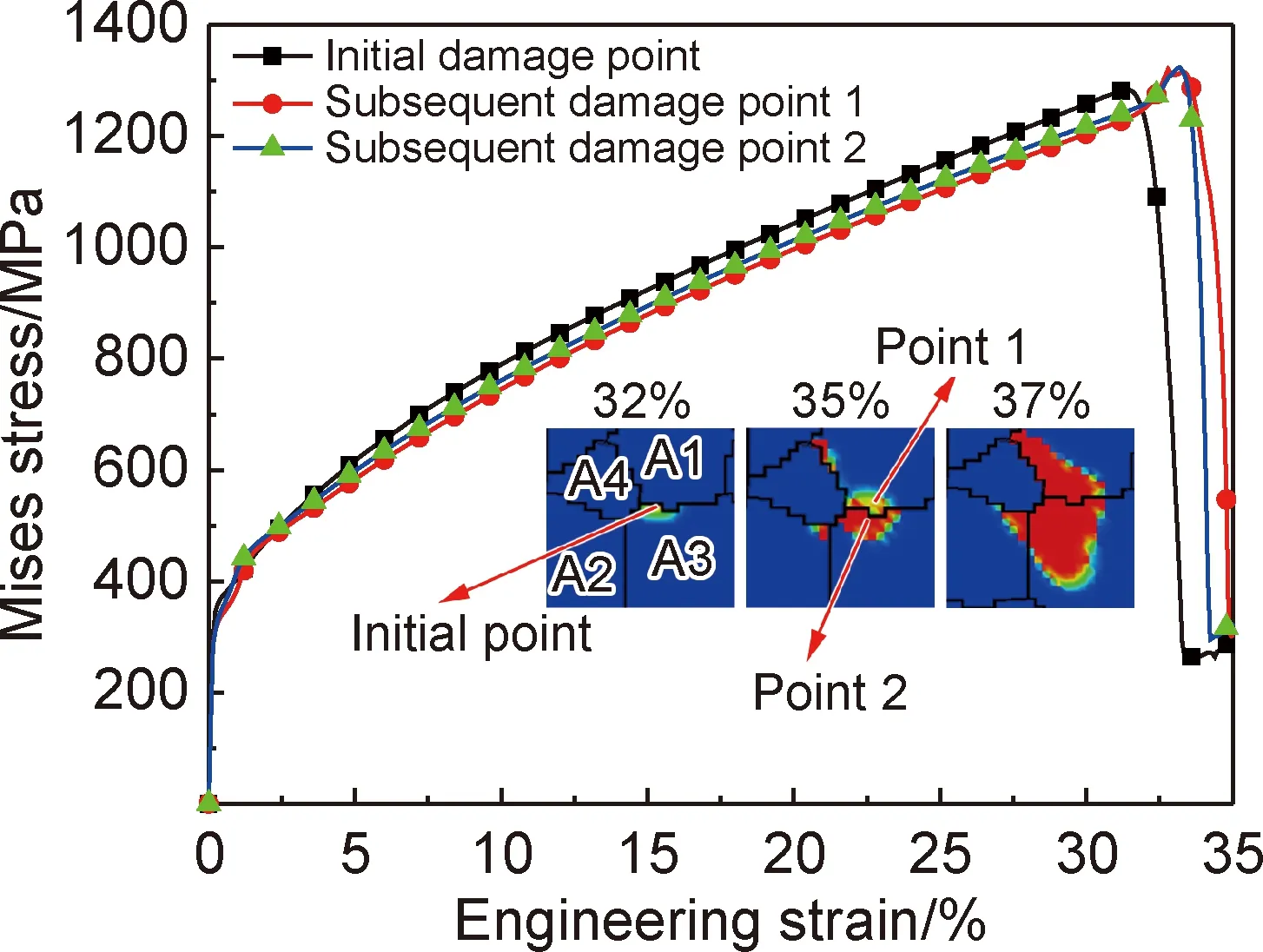
图8 A1～A4晶粒晶界附近不同区域Mises应力随应变的演化曲线及损伤分布云图Fig.8 Mises stress evolution curves with strain and damage distribution contours in different regions near grain boundary of A1-A4 grains

3 结论

(1)考虑位错密度内部状态变量和连续介质损伤因子的CPFEM模型可以较为准确地描述NiCoCrFe的宏观力学行为(应变强化和损伤软化)，并能够合理地捕获颈缩区域的形状和尺寸；实验获得的颈缩区域长度比CPFEM预测结果小7%，且CPFEM预测的颈缩区域宽度比实验结果大23%，CPFEM预测结果与实验存在一定差异，但在合理范围之内。

(2)CPFEM模型可以较为准确预测准静态拉伸条件下NiCoCrFe的织构演化情况。实验和CPFEM模拟获得的NiCoCrFe颈缩区域织构的演化趋势相同，均表现为强(111)∥RD和较弱的(100)∥RD纤维织构。

(3)在三维微观多晶模型拉伸过程中，晶界处发生了明显的应力集中和位错塞积现象；CPFEM模型中滑移系最大剪切应变决定损伤的形成和演化趋势，损伤易形成于三叉晶界处，表现为晶间损伤机制；初始损伤点的软化效应会促进损伤向周围区域快速生长和扩展。