矿井主风机不停风倒机系统最优控制研究*

于保才，邵良杉

(辽宁工程技术大学 系统工程研究所，辽宁 葫芦岛 125105)

0 引言

为保证井下工作人员安全，需要连续不断地为井下提供新鲜空气。按照相关规定，每个回风井处需要安装2套同等能力的通风装置，其中1套作为备用。2台风机需要每月进行1次轮换作业，目前国内大多数煤矿操作流程都是先关闭正在运行的风机，然后将备用风机接入通风系统内，该方法很容易造成瓦斯积聚[1]。因此，研发1套智能控制系统具有十分重要的意义。

国内外很多专家学者提出不停风倒机方案，吴新忠[2]提出的不停风倒机方案已经在国内大多煤矿进行实际应用，但是风量波动依然很大；董素铃[3]提出基于模糊控制的自动控制系统，减小了风量波动，但是对于高瓦斯矿井，依然存在危险；Wang等[4]首次提出动态模型，开发了一种激励控制策略，但是其动态模型运行速度慢。上述方法会使井下风量波动依然很大，或者倒机时间过长，所以还需要进一步改进。

根据上述分析，提出1种基于改进粒子群算法和自适应模糊PID控制的远程智能控制倒机系统，不但能够应用更少的参数，快速找到有效的最佳控制方案，而且通过自适应模糊PID控制能够更精确控制风门的开合角度，从而达到不停风倒机且井下风量基本恒定，能源损耗最少的目的。

1 矿井主要通风机倒机系统结构及原理

煤矿主要通风机倒机系统结构如图1所示，包括2台风机，1台为备用风机，每台风机入风口处分别有1道水平风门和1道垂直风门，当前工作风机是2号风机，当切换指令下达后，首先1号风机开始预热，然后通过控制4道风门，即逐渐关闭1号水平风门、2号垂直风门，同时逐渐开启1号垂直风门、2号水平风门，从而保证井下风量恒定。

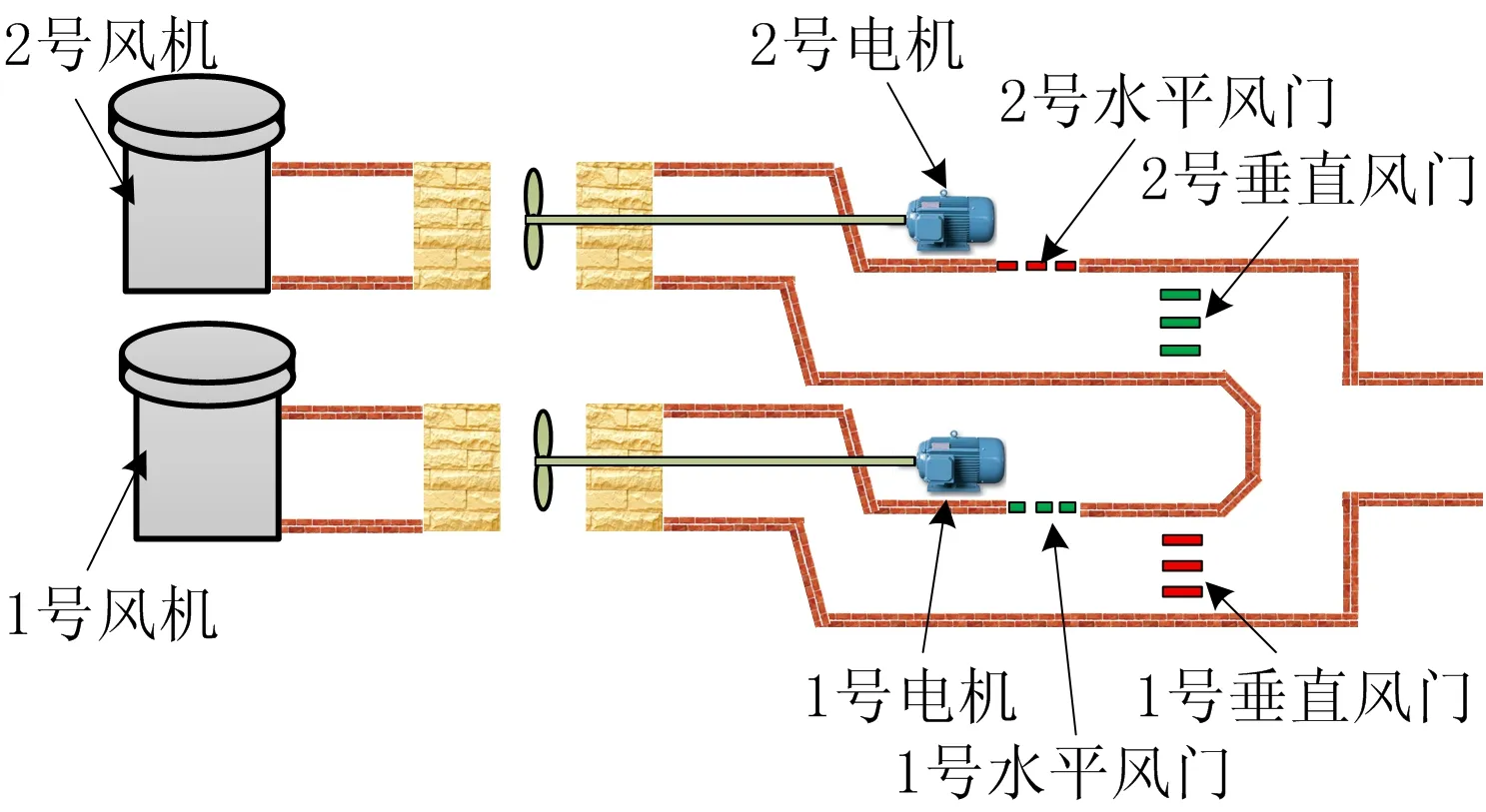
图1 矿井主要通风机切换系统结构Fig.1 Structure of switchover system of mine main fans

文中选用全自动旋叶式风门，其结构如图2所示，其中控制器可以接受来自远程智能控制倒机系统的指令，并将指令传达给百叶窗步进电机，以此更精确控制4道风门的开合角度，从而达到对风量的精确控制。

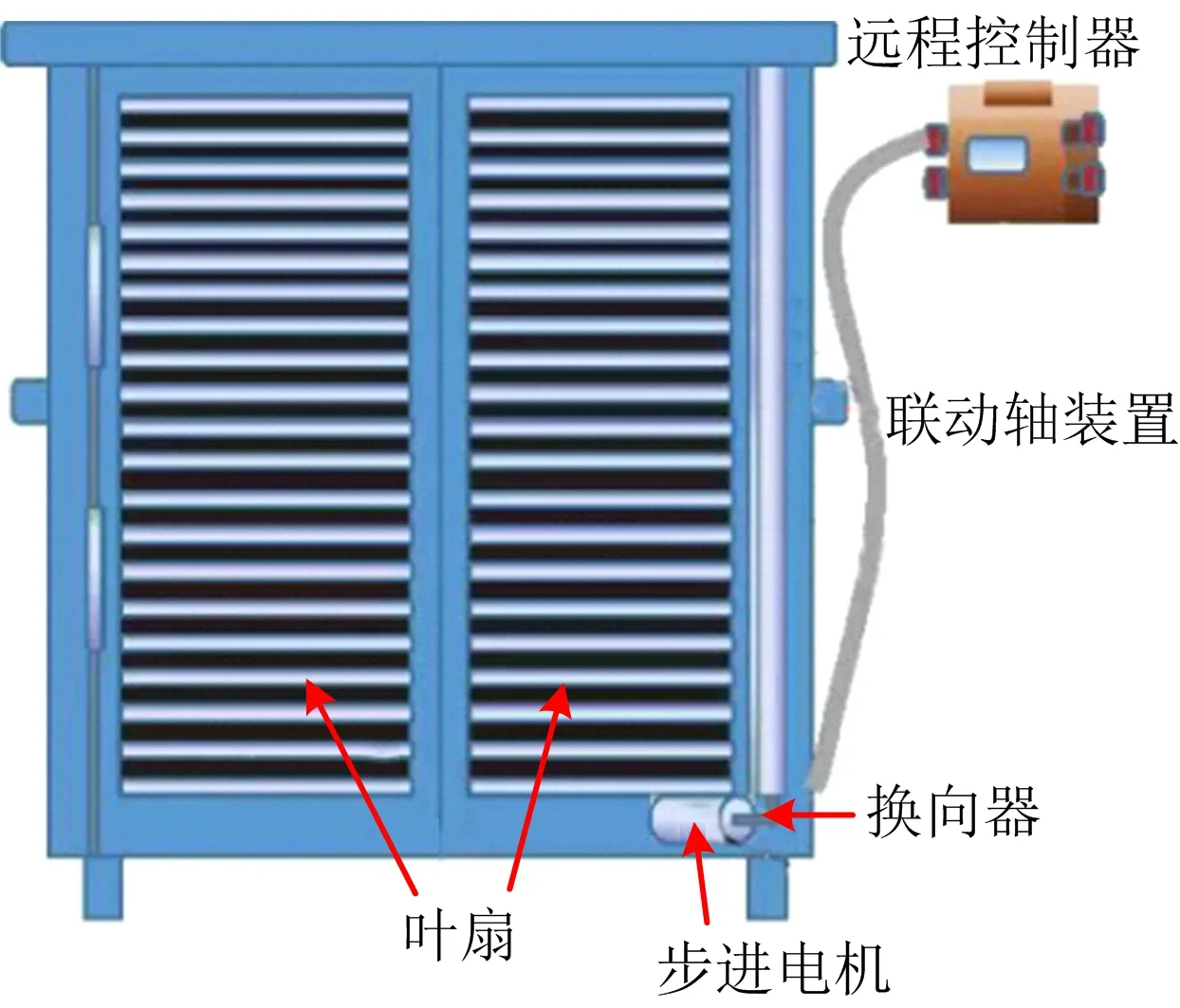
图2 旋叶式远程控制风门Fig.2 Rotating vane type remote control damper

2 矿井主要通风机倒机系统建模

2.1 倒机系统等效模型建立

为方便建立数学模型，将图1所示的结构图简化为如图3所示的等效模型，共8个节点，7条分支，3条虚拟分支；其中M1和M2分别代表2个风机支路，R0，R1S，R1C，R2S，R2C分别表示矿井等效风阻、1号风机水平风门、1号风机垂直风门、2号风机水平风门、2号风机垂直风门。为便于研究风机切换特性，近似认为R0值不变，且巷道内空气不可压缩；节点1表示进风井口，节点5，6表示2个水平风门的进风口，节点7，8表示2台主要通风机排气通道。

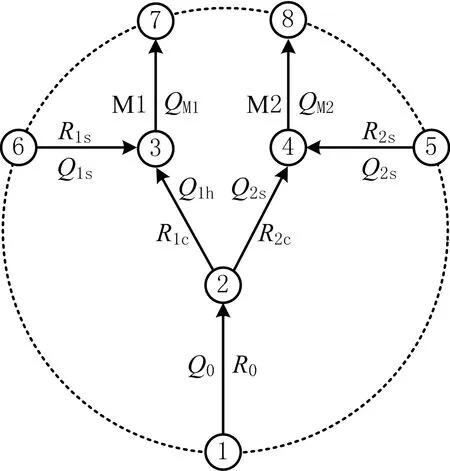
图3 风机切换系统等效模型Fig.3 Equivalent model of fans switchover system

2.2 旋叶式风门特性

系统选用旋叶式风门，不同型号风门风阻可根据式(1)计算。

R=RC×M×w/(2×(w+h))

(1)

式中：R为风门等效风阻，N·s2·m-8；RC为风阻系数；M为风门中叶片数，片；w为叶片宽度，m；h为叶片高度，m。

旋叶式风门的风阻与叶片角度是非线性关系，当叶片角度为0°时候，风阻近似为0，此时风门全开状态；当角度为90°时，风阻接近无限大，此时风门为全闭合状态。根据参考文献[5]，可得到风阻系数RC与叶片角度α的近似数据，图4为用该数据对应得到的拟合曲线，并用Matlab对数据进行5次拟合[6]，得到表达式如式(2)。

(2)

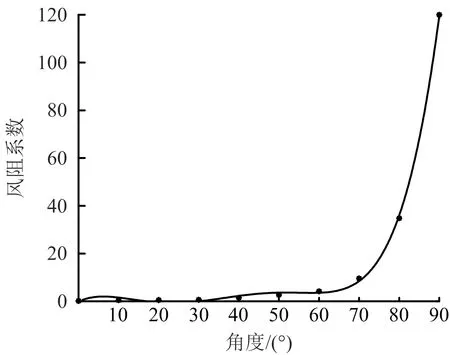
图4 风阻系数与叶片角度曲线Fig.4 Curve of wind resistance coefficient and vane angle

因此，当倒机进行过程中，t时刻通过i号风机的等效风阻可根据式(3)计算得出。

(3)

式中：Rist，Rict表示t时刻i号风机的水平风门、垂直风门的等效风阻，N·s2·m-8，可以通过t时刻风门角度传感器传递回来的角度信息带入到公式(2)中得到。

2.3 主通风机风机特性

在对矿井主要通风机倒机系统进行建模时，为了保证在倒机过程中2台主要通风机工作在安全且高效的状态，需要对风机特性曲线进行进一步研究。中煤华晋王家岭煤矿风机检测报告给出的性能参数见表1。

表1 换算到额定转速、标准通风状态下性能参数值Table 1 Performance parameter values converted to rated rotating speed and standard ventilation state

风机曲线拟合中最常用的方法是二次多项式的最小二乘法拟合，但由于偏差较大[7]，因此，本文选用四次多项式对风机特性曲线进行拟合，图5为用表1中的数据采用四次多项式拟合后的曲线，当风机工况点在A点左侧时候，容易发生喘振，当工作在右侧时候，工作在稳定区域，越接近A点效率越高；图中Rt线与风机特性曲线交点B，代表倒机进行到t时刻风机工况点。

图5 主要通风机风量-风压特性曲线Fig.5 Air volume-wind pressure characteristic curve of main fan

根据表1中的数据，用MATLAB进行四次拟合，得到该主要通风机风量(Q)-风压(H)的表达式(4)。

(4)

2.4 主要通风机倒机系统动态模型

本次建模以井下风量波动最小为目标函数，t时刻井下风量波动可表示为式(5)。

(5)

式中：Q0倒机前井下风量，m3/s；ΔQt，Q0t，Q1ht，Q1st，Q2ht，Q2st，QM1t，QM2t分别指倒机进行到t时候井下风量变化量、井下风量、1号垂直风门风量、1号水平风门风量、2号垂直风门风量、2号水平风门风量、1号风机风量、2号风机风量，m3/s。

由于节点1，5，6，7，8均暴露在大气中，忽略进回风井位置等影响，认为这几个节点压力一致即等于大气压力，因此，可知t时刻通过水平风门的压力和风机压力相等；所以Q1st，Q2st可以用公式(6)，(7)表示。

(6)

(7)

式中：H1t，H2t代表t时刻2台主要通风机的压力即通过水平风门压力，Pa。

计算方法是将t时刻风机风量带入式(4)中，如式(8)，(9)所示，R1st，R2st表示t时刻水平风门的阻力，N·s2·m-8，通过风门角度传感器传输回来的数据，然后代入式(1)中算得该值。

(8)

(9)

当倒机系统运行在t时刻，此时将水平风门、垂直风门、井下风阻共同看成一个等效系统，其等效风阻R1t，R2t可由式(3)求得，如式(10)，(11)所示，此时该系统满足式(12)，(13)关系。

(10)

(11)

(12)

(13)

分别联立式(8)，(10)，(12)和(9)，(11)，(13)，可得到QM1t，QM2t的表达式如(14)，(15)所示。

QM1t=(14.43-9.18×10-41i)R1t

(14)

QM2t=(14.43-9.18×10-41i)R2t

(15)

式中：i为复数。

因此，将式(1)，(6)，(7)，(14)，(15)代入到式(5)中，为了方便表达，令式(1)中除角度以外参数值为ξ，如式(16)所示，最终得到式(17)。

ξ=M×w/(2×(w+h))

(16)

(17)

式中：θ1，θ2，θ3，θ4分别表示t时刻1号风机水平风门、垂直风门叶片角度、2号风机水平风门、垂直风门叶片角度。

转化后的目标函数为式(18)。

(18)

为保证倒机系统安全可靠运行，一般实际工作风压不能超过最高压的90%，倒机时间不能超过10 min。根据实际情况，4个风门调整角度范围为[0°，90°]；由于风门步进电机齿轮精度问题，每步调整角度要大于0.1°，综上所述，约束条件可以表示为式(19)。

(19)

式中：RA为风机工作的最大风阻；Hmax为风机工作的最高风压；Δθ为齿轮角度调整精度。

3 基于改进PSO的模糊自适应PID控制

3.1 模糊PID控制原理

由于矿井主通风机倒机系统中如风量、风压等参数精确度具有一定局限性，因此，应用传统的PID控制算法无法实现该系统的精确、实时调节，因此，本文选用模糊PID控制算法作为该系统的控制部分，能够增强系统鲁棒性，解决倒机系统参数不精确、调控性能不佳的问题。

在矿井主通风机倒机的PID控制系统中，将井下风量变化量作为偏差量e，偏差变化率ec即井下风量的变化率，在输入这2个参数后，模糊控制器根据设定的隶属度函数，选用三角隶属度函数，查询模糊控制表，进行模糊推理过程，然后进行清晰化，清晰化采用目前最常用的重心法，其公式如式(20)所示，清晰化后的参数kp，ki，kd输入到PID控制器中，从而来调节4个风门的步进电机的开合角度和2台风机的电动机的运行状态。

(20)

式中：z0为模糊控制器输出的清晰化后的精确值；zi为模糊控制量轮域内的值；μc(zi)为zi的隶属度值。

3.2 改进PSO算法

PSO算法常用于解决优化问题，通过公式(21)和(22)对粒子移动速度和位置进行不断迭代更新，并时刻记录全局和局部最优解的位置，最终获得最优解[8-9]。

v(i+1)=ωv(i)+c1r1[pbest(i)-x(i)]+c2r2[pgbest(i)-x(t)]

(21)

x(i+1)=x(i)+v(i)

(22)

式中：ω是惯性因子；c1，c2是学习因子；r1，r2为在[0，1]上的均匀随机数。

为了加快算法迭代速度，并且增加PID控制精度，对原始算法进行改进，改进后公式如式(23)所示。

(23)

式中：ωmax，ωmin分别为最初始设置的最大和最小惯性因子；t为当前迭代次数；T为最大迭代次数。

3.3 基于改进PSO的模糊自适应PID控制器

改进PSO算法的模糊自适应PID远程智能风机倒机系统原理框图如图6所示。

图6 改进粒子群算法的模糊PID远程智能控制原理Fig.6 Fuzzy PID remote intelligent control principle of improved particle swarm algorithm

在模糊自适应PID控制算法中kp，ki，kd3个参数对于控制效果有着至关重要的作用，传统算法中一般根据经验设定3个参数，并保持不变，但这样很难保证风机倒机过程中井下风量稳定性。为了能够对风机倒机系统进行动态调整，本文将引入改进粒子群算法，对3个参数进行优化后，输入到PID控制器中，其流程如图7所示。

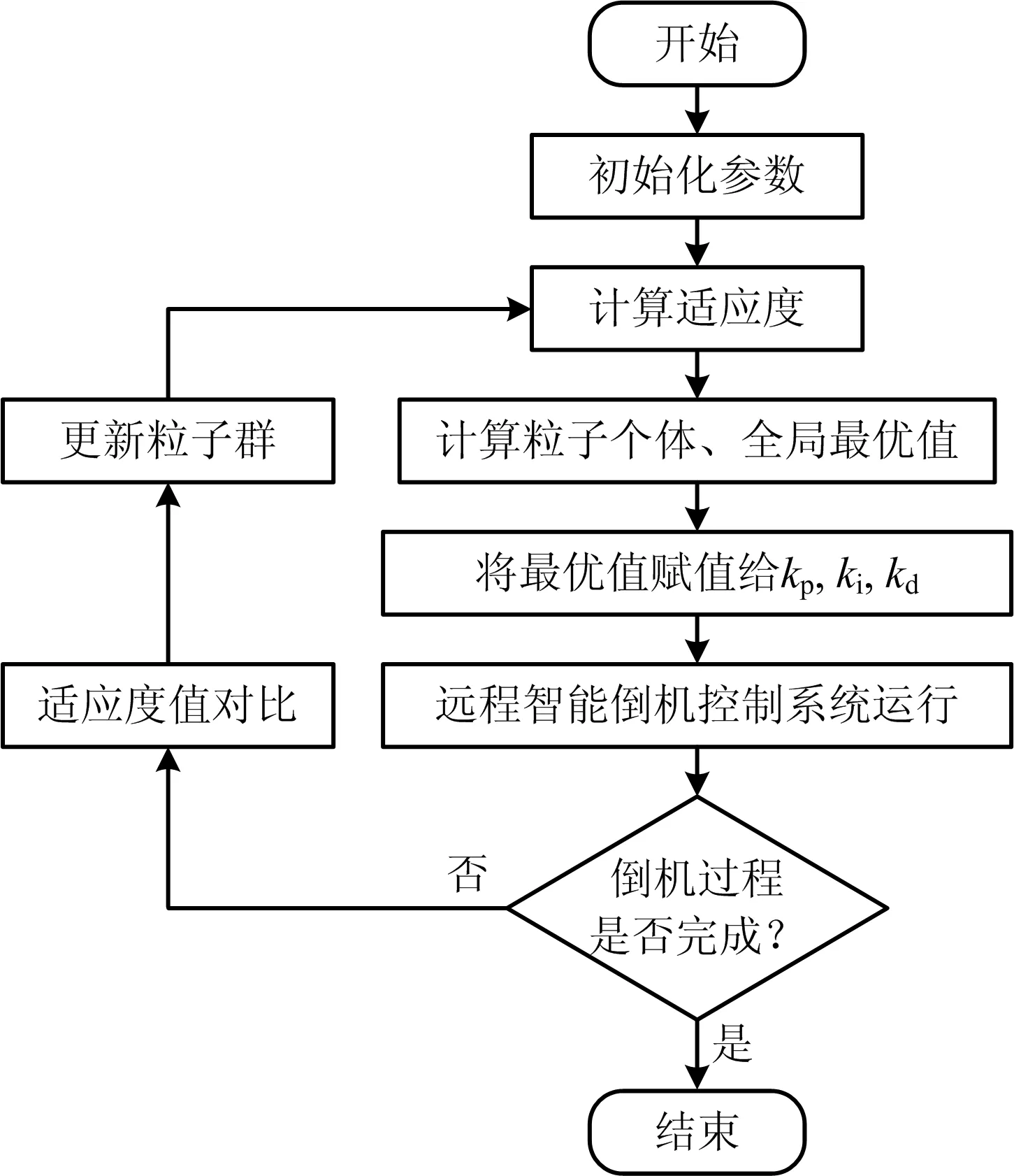
图7 改进粒子群算法优化PID流程Fig.7 PID procedure of improved particle swarm algorithm optimization

4 仿真分析

4.1 仿真设置

为了验证所提方法的有效性，在MATLAB中进行仿真模拟,模糊PID中采用通风系统近似传递函数，如式(24)所示[10]。

(24)

仿真平台及算法主要参数设置见表2。

表2 仿真系统主要参数设置Table 2 Main parameters setting of simulation system

4.2 仿真结果分析

为了验证本文提出方法的有效性，对传统模糊自适应PID算法和IPSO优化的模糊自适应PID算法进行对比，其阶跃响应曲线如图8所示，可看出，模糊自适应PID算法上升较快，但是系统超调现象严重，调节时间大概为25 s左右，动态特性较慢；本文提出的基于IPSO优化的模糊自适应PID算法调节时间为10 s，相比传统PID算法节约60%，并且没有超调现象发生，控制效果明显提升。

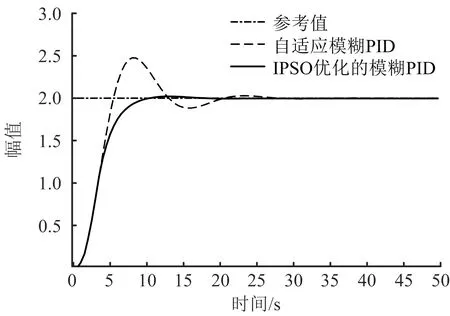
图8 阶跃响应控制效果对比Fig.8 Comparison of step response control effect

图9为优化过程中kp,ki,kd3个参数变化情况，可看出经过一段时间调整kp，ki，kd3个参数逐渐趋于稳定。

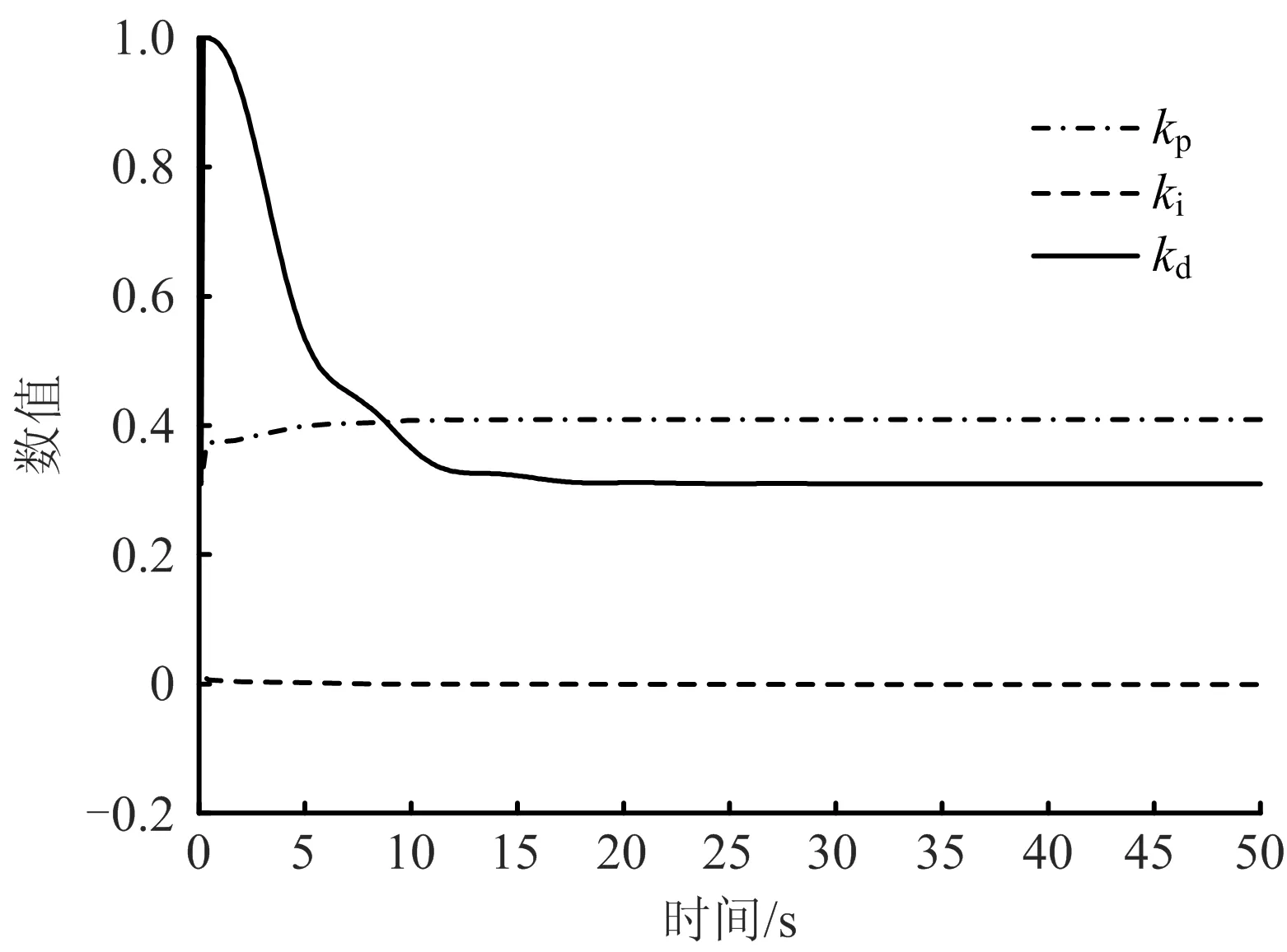
图9 kp，ki，kd参数优化结果Fig.9 Optimization results of kp,ki and kd parameters

图10是在整个系统运行过程中，井下风量的变化量ΔQ随着4个风门调整的变化情况，由图10可知，该系统运行时间为120 s，由于调整开始阶段风门等效风阻随叶片旋转变化较大，因此，风量波动较大，随着系统运行，井下风量变化逐渐稳定，在系统运行后期，同样风门等效风阻变化较大，引起后半阶段的风量波动较大，大概在100 s以后，系统逐渐稳定，运行120 s后整个倒机过程完成。由图10可知系统运行过程中，风量变化量低于0.6%，相比较与文献[11]，[12]调节风量变化率8.1%，5%有了很大提升。

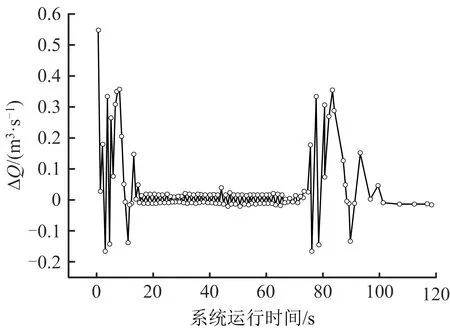
图10 井下风量波动情况Fig.10 Fluctuation of underground air volume

图11是2台主要通风机在倒机运行过程中工况点变化情况，由图11可知，2台风机均工作在稳定工作区域，调整过程中没有发生突跃情况，保证了整个倒机过程的安全可靠性。

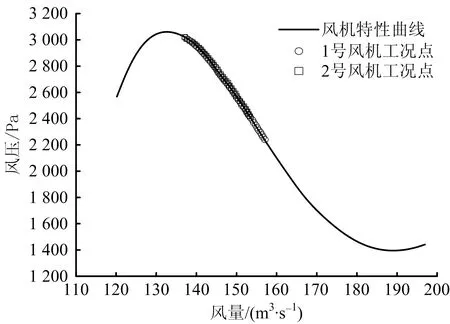
图11 风机工况点变化Fig.11 Change of fan working condition points

5 结论

1)提出煤矿主通风机稳风倒机控制系统的框架模型，研究了该系统各个部分的特性，分别建立其数学模型。

2)建立动态通风机稳风倒机模型，并提出1种改进粒子群优化的模糊自适应PID控制算法对系统进行运算求解。

3)系统运行时间明显缩短，并且没有超调现象；切换过程中井下风量稳定且波动小，2台主通风机一直工作在稳定区间内，没有发生突跃，从而保证该系统的安全性。