公路隧道衬砌病害展布图拼接技术研究
宋 捷,文 宁,王 超
(1. 沈阳联勤保障中心 沈阳市 110000; 2. 辽宁省交通规划设计院有限责任公司 沈阳市 110166)
由于常规检测方法无法准确描绘隧道衬砌病害位置,结果不直观,不利于多年病害的对比,随着隧道机械化、智能化的发展,隧道检测逐步向车载平台化、快速化、信息化方向转变[1]。
1 图像的采集系统概述
由于公路隧道衬砌表面的曲率半径较大,图像获取的范围较大,单个相机无法完整地获取隧道衬砌表面图像,因此需要配置多台相机。本研究为了获取公路隧道每半幅的衬砌表面图像,配置了4台线阵相机。单个线阵相机的图像获取范围3027mm,相邻线阵相机的图像获取重叠范围取30%,为905mm。四台线阵相机总共的图像获取范围为9391mm,可以完整覆盖隧道半幅衬砌表面。在隧道现场一次性完成四个相机的图像获取后,为了直观地展示隧道衬砌图像,需要将四个相机的图像进行拼接,形成完整的半幅隧道衬砌表面图像。四台相机布设方案如图1所示。

图1 采集相机布置方案
2 图像的拼接
图像拼接法就是将多个相关相机的图像无缝拼接在一起以便获得一个宽视角的全景衬砌影像。虽然近年来国内外针对图像拼接各个细节的研究己经取得了一些突破性的成果,但对于尺度、视差和光照强度变化不明显的情况下,其中图像拼接的精确性和准确率仍然亟须加以改善[2]。提出了一种基于隧道特征节点的全自动隧道图像拼接,克服了我国传统的图像拼接工艺中的限制(包括光照、尺度变化的作用及其他因素),实现了多个视角、高精度的图像拼接[3]。
图像的拼接技术由三个方面组成,即图像的配准、图像的融合及图像的插值,图像拼接的工作流程如图2。

图2 拼接流程图
2.1 图像匹配
由于多个CCD相机隧道衬砌进行扫描拍摄,同时由于使用的是线阵相机,所以同一个相机拍摄的图像在采集的过程中就直接拼接为一幅图像,每个相机获得的是多个离散的图像,上下两个相机有30%的重合范围,因此选取30%图像中的特征点。选取重合范围内的特征点,针对上下两个相机中的特征点进行图像匹配,从而将上下两个相机对应位置的图像拼接。
对于重合范围内的特征图像,可以提取角点,通过图像配准来建立变换模型。
一幅图像中的点处的灰度值为I1(x,y),另一幅则表示为I2(x,y),那么用式(1)关系表示图像I1、I2的配准关系:
I2(x,y)=g(I1(f(x,y)))
式中:I1为参考图像;I2为待配准图像;f为2D几何变换函数;g为1D灰度变换函数。
灰度变换的关系并非都是必须要求的,关键在于寻找空间几何变换的关系f(x,y)。忽略了灰度与变换的关系,前面这个关系式可以简化为如式(2):
I2(x,y)=I1(f(x,y))
(2)
同时,将二维相关函数f(x,y)简化成用两个一维相关函数f1(x)、f2(y)相乘来表示,如式(3):
f(x,y)=f1(x)×f2(y)
(3)
在实现图像匹配计算中,系统所占用的计算机内存及CPU便会显著减少,从而大大提高运算效率,节省时间和资源。
左右幅隧道的图像进行匹配的时候,由于隧道检测车的扫描方式不同,会出现反转及镜像的情况,因此,图像的匹配还需要进行相应的几何变换,几何变化的数学意义是将两个坐标系通过相关的计算,融合为一个坐标系。
坐标系的变换可通过坐标系的平移、坐标系的旋转和坐标系的反转组合来实现,表征一幅图像中两点间的距离通过相关数学的变换,达到另一图像的坐标系。变换公式如式(4):
其中,tx和ty为平面平移量;θ为平面旋转角度。
在二维空间中,多项式代数变换通常可以用来作为一种非常典型的非线性代数变换,变换的代数公式及其定义如式(5):
x′=a00+a10x+a01y+a20x2+a11xy+a02y2
y′=b00+b10x+b01y+b20x2+b11xy+b02y2
(5)
对于一个具有完全局域形变的图像和一个局部没有完全形变但是整体接近刚体的图像,在进行配准时使用非线性变换方法可以很好地来实现。
2.2 图像融合
通过图像的匹配之后,找到相应的特征对应点,然后将两幅图像拼接在一起,获取更为全面、可靠的图像,此种做法叫做图像的融合。图像融合可分为三类:像素级融合、特征级融合和决策级融合。为了更好地得到一个合成的图像,必须选择一种合适的方法进行图像与融合的策略。
对于待拼接的两幅图像,配准后的图像之间相互重叠的区域中每个像素点的灰度值应当采用重叠区域平均值。设有两幅代表混合后的图像为f,f1和f2分别是等价于待拼接的图像,则会有式(6):
f(x,y)=
(6)
式中:w1和w2分别为重叠区域中两幅图像对各自像素的权重值,权重值同时满足w1+w2=1,0 如何选择适当的权值,具有重要意义,恰当的权重值可使两幅图像的重叠区域平滑过渡,进而消除拼接痕迹,使之达到同一副图像的视觉效果。在此介绍一种简易的权值的选取方法实际测试发现,两幅图像的重叠区域像素的权值的大小取值与特征点像素到图像的边缘垂直距离呈现一定的相关性,因此,有式(7): f(x,y)= (7) 式中:f为融合后的图像;f1和f2分别为寻找到特征点的两幅图像;d1和d2为权重,一般di=1/width(width表示两幅图像重叠宽度),且d1+d2=1,0 图3 权重值变化图 对图像进行配准时,根据相应的匹配性和特征进行比较,可以构建出一种数学模型。根据简单的变换模型就能够将图像转移到同一个坐标系下,变换后的点坐标往往与三角形中的点坐标相反,也就是它们分别位于四个输入像素之间,这就导致拼接后的图像会出现有空洞。要想避免此种现象,需要采取插值技术。 使用点4个最近相邻像素灰度值依次计算,灰度值按照如图4所示进行计算。假定设点(x′,y′)的四个最近相邻像素是a、b、c、d。他们的位置坐标是(i,j)、(i+1,j)、(i,j+1)、(i+1,j+1)。他们的灰度值分别表示为g(A)、g(B)、g(C)、g(D)。E和F两点之间的灰度平均值公式g(E)、g(F)为: 图4 双线性插值 g(E)=(x′-i)[g(B)-g(A)]+g(A) g(F)=(x′-i)[g(D)-g(C)]+g(C) 则(x′,y′)点的灰度值g(x′,y′)为: g(x′,y′)=(y′-j)[g(F)-g(E)]+g(E) 插值采用三角形线性函数来表达,插值运算核如图5所示,计算公式见式(8)。 图5 插值函数核 (8) 插值的方法有多种,如最近邻插值法、双线性插值法、三次卷积插值法,而在工程的实际应用过程中,为了减少计算量,同时获得较好的效果,通常采用双线性插值法。 图6是同一个相机连续拍摄的三张图像,拼接结果如图7所示。 图6 一个相机拍摄的连续三张图 图7 拼接结果 图8为两个相机在同一时刻采集的图像,经过拼接,得到的结果如图9所示。 图8 上下两相机同位置照片 图9 两相机拼接照片 四个相机拍摄图像及拼接效果如图10~图14所示。 图10 相机1获取的隧道衬砌图像 图11 相机2获取的隧道衬砌图像 图12 相机3获取的隧道衬砌图像 图13 相机4获取的隧道衬砌图像 介绍了公路隧道衬砌图像匹配、融合、插值等方法,相关方法已应用于辽宁省隧道定期检测工作实践。结果表明,该图像拼接方法切实可行、成像良好,为后续隧道检测技术研究提供了新的思路与途径。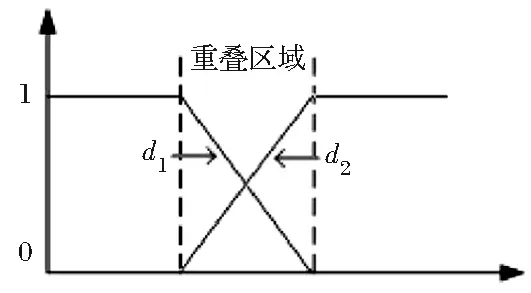
2.3 图像的插值
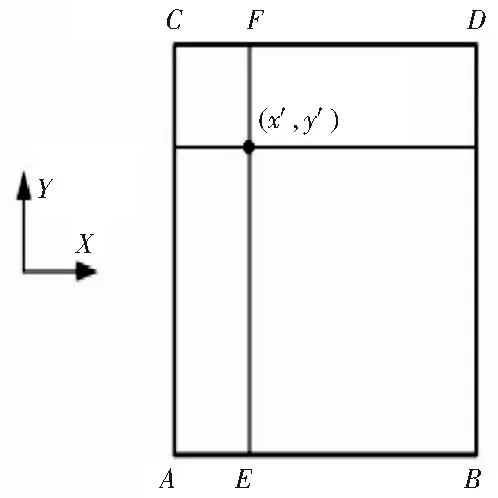
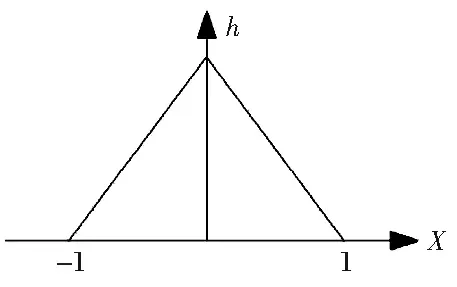
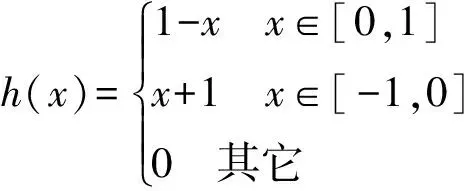
3 拼接实例
3.1 单相机拼接样例


3.2 两相机拼接样例


3.3 多相机拼接样例




4 结语

