两类差分方程组非双曲零平衡点的渐进稳定性
查明鑫,谢 涛,司文晓
(湖北师范大学 数学与统计学院,湖北 黄石 435002)
0 引言
差分方程作为现实世界中描述离散现象的模拟,在生物数学,生物工程,种群动力学,统计学,遗传学等科学领域有重要应用。近年来,一些特殊的差分方程的解的性质引起了人们研究的兴趣[1~17]。2000年G.Ladas在文献[1]中研究了一类生物模型解的全局行为,即指数型差分方程
xn+1=axn+bxn-1e-xn,n=0,1,…
解的稳定性和半循环性,这个方程刻画了多年生草地凋落物的数量。随后,文献[2]又将这一数量模型用于研究生物数量,得到了a为人口迁移率,b为人口净增长率时的人口数量模型。
2003年文献[3]基于离散的流行病模型,研究了差分方程
正解的振动性,全局渐近稳定性等性质。2010年文献[4]从自动控制理论出发,研究了一类极大值型差分方程正解的有界性。随后2012年文献[5]中给出了一类三阶差分方程组的解的表达式,进而对解的全局行为进行了分析。文献[6]提出了一种二维乘积型差分方程组,给出了其封闭形式的通解公式。2015年文献[7]首次利用稳定性理论的已知结果考虑了具有随机扰动的指数型非线性差分方程系统,当系统的正解收敛于系统的两个平衡点中的某一个时,得到了一个具有随机扰动的初始非线性系统的两平衡点的概率稳定性的充分条件。文献[8]提出了带时滞的Lotka-Voltera离散型竞争系统,给出了一个系统持久性的充要条件。差分方程的发展经历了由单个方程到差分方程组的过程[3~9],参数个数和方程数目的增加对方程解讨论的难度增大,改进后的模型能更近似地描述实际问题,但方程的具体形式变得复杂多样,其研究方法并未统一,文献[10~14]分别对差分方程作出了定性分析,直到中心流形理论的出现,方程解的性质才得到更精确的刻画。
文献[9]开始研究一些耦合的差分方程,扩展了原来的生物数学模型。文献[10]中给出了一类描述经济模型的差分方程组,讨论了经济领域中离散模型系统的全局定性行为。文献[11,12]对一维生物模型进行了自然推广,研究其唯一非负平衡的存在性和稳定性。
在文献[13]中,作者研究了
xn+1=axn+byne-xn,yn+1=cyn+dxne-yn
(1)
和
xn+1=ayn+bxne-yn,yn+1=cxn+dyne-xn
(2)
在平衡点是双曲型的条件下的解的性质,其中a,b,c和d是实数,x0,y0为正数。一个自然的问题是, 若上述系统的零平衡是非双曲型的, 则(1)和(2)的解的渐进行为与参数a,b,c和d的关系会是怎样的?
本文运用中心流形定理研究了这一问题,分别给出了系统(1)和(2)的平衡点是非双曲型条件下渐进稳定的若干充分条件。
1 预备知识
考虑差分方程
xn+1=F(xn)
(3)
其中函数F∶k→k连续。 设u*是F的一个不动点, 即F(u*)=u*.经过平移,不失一般性,设u*=0k. 用C=DF(0k)表示方程(3)的线性化方程在0k处的系数矩阵。设C有t个特征值位于复平面的单位圆周上,有s个特征值位于单位圆内部,则方程(3)可以改写成如下的方程组

(4)
其中

(5)
是方程(3)的雅可比矩阵,A为t×t矩阵且其所有特征值位于复平面单位圆周上,B为s×s矩阵且其所有特征值位于单元圆内部,t+s=k;f∶k→t,g∶k→s是非线性函数且满足f(0t,0s)=0t,g(0t,0s)=0s,Df(0t,0s)=0t,k,Dg(0t,0s)=0s,k.
引理1 (文献[17])方程(4)存在中心流形,即存在函数h∶t→s满足h(0t)=0s,
Dh(0t)=0s×t且方程
yn+1=Ayn+f(yn,h(yn)),n=0,1,…
(6)
的动力学性质决定了方程(2)的动力学性质。具体为若是方程(6)的稳定(渐进稳定,不稳定)的不动点,则0k是方程(3)的稳定(渐进稳定, 不稳定)的不动点。
一般地, 不易得到函数h(x)的具体表达式, 但是由下面的引理可知, 可以得到h(x)的一个近似表达式。
引理2 (文献[17]) 设ψ∶t→s是一阶光滑函数且满足ψ(0t),=0s,Dψ(0t)=0s×t,F是方程(3)中所给函数, 若存在r>1使得F(ψ(x))=o(‖x‖r)(x→0), 则
h(x)=ψ(x)+o(‖x‖r)
其中h是引理1中所定义的函数。
关于一维差分方程的稳定性,有如下结论:
引理3 (文献[3]) 设方程(3)的函数F∶→存在不动点u*,以下两条成立:
1) 若F′(u*)=-1且SF(u*)<0,这里S是施瓦兹导数, 定义如下
则u*是渐近稳定的。
2)若F′(u*)=1且F″(u*)≠0,则u*是不稳定的。
引理4 若a,b,c,d∈且满足
(1+a)(1+c)=bd,-2 (7) 则方程中由系数a,b,c,d组成的雅可比矩阵 (8) 有一个特征值λ1=-1和另一特征值λ2<1. 证明 由J的特征方程p(λ)=λ2-λ(a+c)+ac-bd=0,又因为(7)式中两条件成立,得到λ1=-1是J的一个特征根。其次,将λ1=-1代入特征方程p(λ)中,分解因式可得多项式 p(λ)=(λ+1)(λ-a-c-1),因此λ2=a+c+1也是J的一个特征根。又由于(7)式中第二个不等式成立,易得|λ2|<1. 下面利用中心流形定理,给出方程(1)零平衡点渐进稳定的若干充分条件。 定理1 假设差分方程由(1)给出,其中初始值x0,y0∈,若a,b,c,d满足下列条件1或条件2,则方程(1)的零平衡点是渐进稳定的,其中 条件1a,b,c,d满足(7)式及 (9) 条件2a,b,c,d满足(7)式及 (10) 这里 和 则方程(1)的零平衡点是渐近稳定的。 证明 初始方程(1)可以写成如下形式 (11) 其中 f(x,y)=by(e-x-1),g(x,y)=dx(e-y-1) 现令 其中T是J的对角化矩阵 (12) 那么(11)式可写成 (13) 这里 db2(u+v)(e(a+1)u-(1+c)v-1)) db2(u+v)(e(a+1)u-(1+c)v-1)) (14) 作变换v=h(u),用ψ(u)作为h(u)的逼近,即令h(u)=ψ(u)+O(u4)和ψ(u)=Au2+Bu3,其中A和B是实数。根据引理2,结合式(13)和(14),研究方程组(1)零平衡点的稳定性转变为研究下列差分方程的稳定性 (15) 计算函数G得 G(un)=-u+(c1+c2u2+c3u3)(ec4c5u2+c6u3-1)+(c7+c8u2+c9u3)(ec10c11u2+c12u3-1) (16) 其中ci,i=1,2,…,12是与a,b,c,d,A有关的参数, 形式如下 (17) 由(13)式得 即 那么 因此 (18) 由(16)式,得G′(0)=-1且 (19) 根据式(17)~(19)和方程(7),有 其中 h(b)=(3a2+4a+c2)b2-2(a+1)(a-c)2b+(a+1)2(3c2+4c+a2) (20) 现讨论第一种情况:若(7)式和条件(1)成立,注意到h(b)是关于b的一元二次函数,ρ2为h(b)的一个根,下证 h(b)>0 (21) 令(20)中根的判别式为 Δ=(a-c)4-(3a2+4a+c2)(3c2+4c+a2) 整理得 Δ=-2(2+a+c)(a3+a2c+c3+4ac+ac2) (22) 3a2c+4ac+c3<0 (23) 因a<0,由(23)可得 a3+a2c+c3+4ac+ac2=a(a-c)2+3a2c+4ac+c3<0 (24) 由(7)式中条件-2 其中SG(0)是施瓦兹导数。这说明线性差分方程(15)的零平衡点是渐近稳定的,根据引理3,初始系统(1)的零平衡点也是渐近稳定的。 第二种情况若(7)式和条件2成立,注意到ρ1和ρ2是(20)式中h(b)的两根。(10)式中有 下面,利用中心流形定理研究方程(2)零平衡点的渐进稳定性。 引理5 若a,b,c,d∈,且满足 (1+b)(1+d)=ac,-2 (25) 则方程中由系数a,b,c,d组成的雅可比矩阵 有一个特征值λ1=-1和另一特征值λ2<1. 证明 由J的特征方程p(λ)=λ2-λ(b+d)+bd-ac=0,又因为(7)式中两条件成立,得到λ1=-1是J的一个特征根。其次,将λ1=-1代入特征方程p(λ)中,分解因式可得多项式 p(λ)=(λ+1)(λ-b-d-1),因此λ2=b+d+1也是J的一个特征根。又由于(7)式中第二个不等式成立,易得|λ2|<1. 定理2 假设差分方程由(2)给出,其中初始值x0,y0∈,若a,b,c,d满足下列条件3或条件4或5,则方程(2)的零平衡点是渐进稳定的,其中 条件3a,b,c,d满足引理4及 (26) 条件4a,b,c,d满足引理4及 (27) 条件5a,b,c,d满足引理4及 (28) 则方程(2)的零平衡点是渐近稳定的。 证明 原始方程(2)可写成 (29) 其中 f(x,y)=bx(e-y-1),g(x,y)=dy(e-x-1) 令 其中T是J的对角化矩阵 (30) 则(29)式可写成 (30) 这里 (31) 作变换v=h(u),用ψ(u)作为h(u)的逼近, 令h(u)=ψ(u)+O(u4)和ψ(u)=Au2+Bu3,其中A和B是实数。根据引理2,(30)和(31)式,研究方程组(2)式零平衡点的稳定性转变为研究下列差分方程的稳定性。 (32) 计算得函数G为 G(u)=-u+(c1+c2u2+c3u3)(ec4c5u2+c6u3-1)+(c7+c8u2+c9u3)(ec10c11u2+c12u3-1) (33) 其中ci,i=1,2,…,12是与a,b,c,d,A有关的参数, 形式如下 (34) 由(30)可得 即 整理后得 经计算 (35) 由(33)式,可见G′(0)=-1且(19)式成立,那么根据(19)(34)和(35)式,有 (36) 首先假设(7)式和条件3成立。现证明G‴(0)>0.由(26)式,有b-d>0,1+b>0,因为 (37) (38) 因此,结合(36)~(38)式,可得G‴(0)>0. 现假设(7)式和条件4成立,则有b-d<0,1+b<0,2+b+d>0,那么 (39) 因此G‴(0)>0. a2d+b(1+b)(1+d)<0.即G‴(0)>0. 因此,可得SG(0)<0,其中SG(0)是施瓦兹导数。这说明差分方程(32)式的零平衡点是渐近稳定的。由引理2~3,差分方程(2)式的零平衡点也是渐近稳定的。 考虑如下差分方程组 xn+1=axn+byne-xn yn+1=cyn+dxne-yn (40) 取a=-0.7,c=0.5,在定理3中计算出D=0.7082,ρ2=-1.0555 ,ρ1=0.2556, 得到b的范围-1.0555 在(40)式中令初值,x0=0.2,y0=-0.2 ,画出其对应图像,见图1和图2. 图1为迭代100次时的方程组解曲线,图2为迭代2 500次时的方程组解曲线。通过计算a,b,c,d可得G‴(0)>0, 即SG(0)<0,从图1和图2中可以看出差分方程(40)式的零平衡点是渐近稳定的。
2 主要结论
2.1 方程(1)零平衡点的渐进稳定性








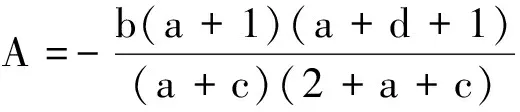



2.2 方程(2)零平衡点的渐进稳定性



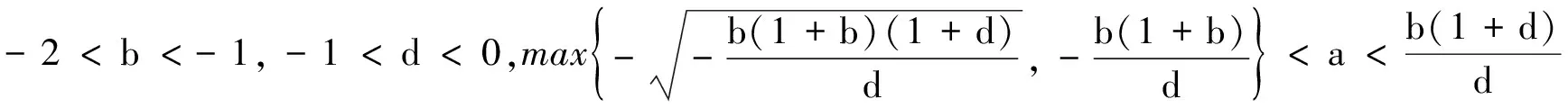


















3 应用举例



