学习迁移理论在高等代数教学中的应用

安军

学习迁移理论在高等代数教学中的应用

安军

（重庆工商大学 数学与统计学院，重庆 400067）

为了促进学习的正迁移，防止学习负迁移，并形成完整的认知结构，研究了学习迁移理论在高等代数教学中的应用策略，提出强化概念的类比，强化定理的类比，培养归纳总结能力，培养发散思维能力等具体措施．通过学习的正迁移，极大地提高了学生的学习兴趣，培养了数学探究能力，取得了较好的教学效果．

学习迁移；类比；发散思维；探究能力；高等代数

所谓学习迁移是指一种学习对另一种学习的影响．如果一种学习对另一种学习起到促进作用，则称这种迁移为正迁移；如果一种学习对另一种学习起到干扰作用，则称这种迁移为负迁移[1～2]．迁移是数学学习中的普遍现象，教学中要努力促进学习的正迁移，防止学习负迁移，引导学生弄清前后知识的区别与联系，形成完整的认知结构．

高等代数是研究多项式、矩阵、线性空间和线性变换的一门数学学科，其概念和定理较多，且不少概念、定理和方法在名称或意义上具有高度的相似性或逻辑原理一致性，很容易使学生产生知识混淆．所以，教师要善于运用学习迁移理论指导高等代数教学，加深学生对知识的理解，促进学习的正迁移；避免前后知识相互混淆，防止学习负迁移．

本文研究了学习迁移理论在高等代数教学中的应用策略，提出强化概念的类比，强化定理的类比，培养归纳总结能力，培养发散思维能力等具体措施，通过引导学生知识关联、方法拓展和命题改进等手段，培养其数学探究能力．

1 强化概念的类比

在高等代数教学中，要引导学生注意相似概念和相关概念的类比．相似概念包含3种情况：第1种是名称相似，但其内涵不同；第2种是名称不同，内涵相似，存在的背景不同；第3种是名称不同，内涵相似，外延不同．对于相关概念，从表面上看，概念名称或内涵并无相似之处，但是通过逻辑演绎发现，它们之间却有高度的关联性，甚至逻辑原理的一致性．分别举例说明相似概念和相关概念这2类概念如何进行类比，恰当运用学习迁移理论促进学习的正迁移．

1.1 强化相似概念的类比

1.1.1 名称相似，内涵不同 向量组的线性相关和线性无关，其名称相似，但内涵对立．前者是说，存在一组不全为零的数，使向量组的线性组合为零；后者是说，是如果一个向量组的线性组合为零，则组合系数必全为零．由于概念内涵完全相反，因此，它们的性质也完全对立．教学中要注意引导学生在进行逻辑否定时，将内涵对立的概念名称互换．如对于命题：如果一个较多（指包含向量个数的多少）的向量组可由一个较少的向量组线性表示，则较多的向量组线性相关．其逆否命题则应说成，如果一个线性无关的向量组可由另一个向量组线性表示，则无关向量组包含的向量个数不会多于另一个向量组包含的向量个数[3]．

1.1.2 名称不同，内涵相似，存在的背景不同 向量组的极大无关组、秩与线性空间的基、维数，这2组概念名称不同，但内涵相似，仅仅是概念存在的背景不同．极大无关组和秩是针对向量组而言的，基和维数是针对线性空间而言的．如果把线性空间看成是一个向量组，则基就是它的极大无关组，维数就是向量组的秩．由于概念的内涵相似，所以在不同的背景下它们对应的性质是相似的．如秩和维数分别是向量组和线性空间的不变量，极大无关组和秩、基和维数分别代表了向量组和线性空间的最简结构．

图1 矩阵等价、相似与合同的关系

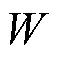
1.2 强化相关概念的类比

在欧氏空间中，正交变换和对称变换是2个不同的概念，但是，正交变换在任一标准正交基下的矩阵是正交矩阵，对称变换在任一标准正交基下的矩阵是对称矩阵，这2个性质是相似的．

在高等代数中类似实例还很多，教师要注意引导学生弄清这些概念在逻辑上的相似关系或等价关系，促进学生形成完整的认知结构．

2 强化定理的类比

在高等代数定理的教学中要强化名称相似或意义相似定理的类比，促进学习的正迁移．

2.1 名称相似定理

2.2 意义相似定理

强化意义相似定理的类比，促进学习的正迁移．如关于子空间和的维数定理

直和的维数定理

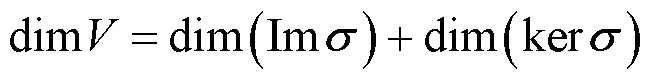
欧氏空间正交补的维数定理

两个有限集合元素个数的定理

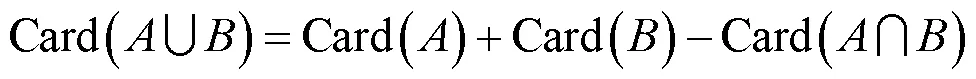
3 培养归纳总结能力

在高等代数中往往同一个概念下导出多个结论，或同一个问题有多种解法．教学中要注意引导学生对知识和方法进行归纳总结，将知识进行压缩，便于分类和记忆．同时加深对知识和方法的理解，形成思维定势，促进学习的正迁移，培养学生归纳总结的能力．

学完行列式的计算后，引导学生总结行列式这章的知识重点是行列式的计算、克莱姆法则．总结行列式的计算方法，即化三角形法、降阶法、加边法（升阶法）、分离法（分成2个行列式相加）、递推公式法、数学归纳法等．在学完矩阵的乘法运算规则后，引导学生总结并记住特殊矩阵相乘的结果，如在教材[3]中总结了应记住的６种特殊矩阵相乘的结果．在学完初等矩阵之后，引导学生总结逆矩阵的计算方法，即待定系数法、伴随矩阵法、与单位矩阵拼在一起运用初等行（或列）变换法．其中待定系数法通常用于低阶的分块矩阵，伴随矩阵法通常用于低阶数字矩阵，最后一种对高阶数字矩阵（或分块矩阵）而言是最好的方法．

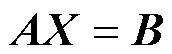
如果学生不注意归纳总结，没弄清各种方法适用范围，容易前后知识干扰，造成学习负迁移．

4 培养发散思维能力

发散思维也称求异思维或变异思维，是从同一来源材料或同一个问题，探求不同方法的思维过程[4]．数学训练对青少年的心智、潜能的开发是深刻且长远的，而且是其它学科所不能替代的[5]，在数学教育中培养发散思维能力是开发学生心智潜能的重要途径之一．发散思维能力主要包括知识关联能力、方法拓展能力和命题改进能力．

4.1 培养知识关联能力

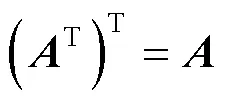
由于线性变换空间与矩阵空间同构，它们具有相同的代数性质，因此，讲解线性变换或向量时关联矩阵（方阵）或坐标；讲解线性变换值域的维数关联矩阵的秩、线性变换核空间的基关联齐次方程的基础解系等．在同构意义下，将这些概念相互转换可得到高等代数的几何法与解析法间的相互等价性[6]．

4.2 培养方法拓展能力

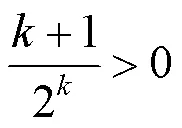
教师要强调不能将霍尔维兹定理推广于判定半正定二次型，即当二次型的矩阵的各阶顺序主子式全部大于或等于零时不能判定该二次型是半正定二次型．

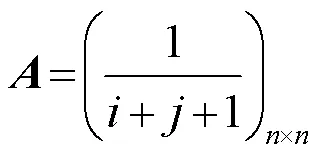
4.3 培养命题改进能力

培养命题改进能力，促进学习的正迁移．教师要引导学生对一个数学命题进行思考：（1）其逆否命题如何叙述；（2）其逆命题（或否命题）是否成立；（3）改变命题条件，结论将如何改变．

也可引导学生思考：能否把一个对可逆矩阵成立的命题推广到对一般方阵也成立．

例4所给出的方法通常叫矩阵摄动法，这是将非奇异矩阵成立的命题推广到一般矩阵成立的命题时常用的一种方法[10]．

5 结语

学习迁移理论是教育心理学的重要理论，教师要经常运用这一理论指导高等代数教学，强化前后概念的类比，强化定理或方法的类比，厘清它们的区别和联系及应用范围．同时要注意培养学生的归纳总结能力，培养发散思维能力．引导学生通过类比、归纳和总结加深对知识的理解，促进学习的正迁移；避免概念、定理或方法相互混淆而出现学习负迁移，并通过知识关联、方法拓展、命题改进等手段，培养学生的数学探究能力．

[1] 曹才翰，章建跃. 数学教育心理学[M]．3版．北京：北京师范大学出版社，2014．

[2] 孔凡哲，曾峥．数学学习心理学[M]．北京：北京大学出版社，2009．

[3] 安军，蒋娅．高等代数[M]．北京：北京大学出版社，2016．

[4] 陈在瑞，路碧澄．数学教育心理学[M]．北京：中国人民大学出版社，1992．

[5] 李忠．数学的意义与数学教育的价值[J]．课程教材教法，2012（1）：58-62．

[6] 安军．谈高等代数的解析法与几何法[J]．高等数学研究，2019，22（4）：60-63．

[7] 安军．矩阵秩的性质及秩不等式的五种证法[J]．高等数学研究，2020，23（4）：96-99．

[8] 黄廷祝，李永彬，何军华．高等代数[M]．2版．北京：高等教育出版社，2016．

[9] 杨子胥．高等代数习题解：下[M]．济南：山东科学技术出版社，2001．

[10] 姚慕生，谢启鸿．高等代数[M]．3版．上海：复旦大学出版社，2015．

The application of learning transfer theory in advanced algebra teaching

AN Jun

（School of Mathematics and Statistics，Chongqing Technology and Business University，Chongqing 400067，China）

In order to promote the positive transfer of learning，prevent the negative transfer of learning，and form a complete cognitive structure，the application strategy of learning transfer theory in advanced algebra teaching is studied, and specific measures are put forward such as strengthening the analogy of concepts, strengthening the analogy of theorems，cultivating the ability of induction and summary，and cultivating the ability of divergent thinking．Through the positive transfer of learning，students′ learning interest is greatly improved，their mathematical inquiry ability is cultivated，and good teaching results are obtained.

learning transfer；analogy；divergent thinking；research ability；advanced algebra

O151.2∶G642.0

A

10.3969/j.issn.1007-9831.2022.02.016

1007-9831（2022）02-0082-07

2021-10-08

重庆市教委高等教育教学改革研究一般项目（213203）

安军（1964－），男，四川安岳人，副教授，硕士，从事高等代数教学研究. E-mail：scottan@sina.com