疲劳微裂纹的非线性兰姆波静态分量检测研究

刘长军， 许子圣， 朱武军， 项延训

(华东理工大学，上海 200237)

0 引 言

受到疲劳载荷、温度波动及腐蚀介质等影响，疲劳微裂纹往往会在服役金属结构内部或表面萌生并不断扩展，严重影响金属结构的安全运行[1-2]。因此，疲劳微裂纹的检测对保障金属结构服役安全具有重要意义。传统超声兰姆波检测技术基于超声波在缺陷处的反射、透射及衰减等现象，一般用于检测宏观缺陷及开口裂纹，而对疲劳微裂纹的检测不敏感。非线性超声兰姆波检测技术利用有限振幅超声与疲劳微裂纹非线性相互作用生成的高次谐波、混频波和静态分量等信号，是一种检测结构微裂纹的有效手段[3-4]。

国内外学者对非线性超声兰姆波检测方法开展了大量研究，但大多局限于兰姆波二次谐波，兰姆波模式对的选择需要满足相速度匹配和非零能量流等严苛共振条件[5-6]。相对于二次谐波，兰姆波静态分量以信号强度大、衰减小和不需相速度匹配条件等优势，近几年逐渐受到研究者们的关注[7-10]。在发生效应方面，Sun等[7]和Wan等[8]分别基于理论解析和仿真模拟，分析了弹性固体中非线性兰姆波静态分量的累积生成。研究表明相速度匹配是静态分量幅值累积增长的非必要条件，并且非线性兰姆波静态分量仅为S0模式。在测量方法方面，Sun等[9]和Deng[10]分别提出了采用激光干涉仪和低频压电换能器接收静态分量的实验测量方法。而关于材料损伤的非线性兰姆波静态分量检测尚少有报道，仅有Sun等[9]采用非线性兰姆波静态分量检测了Al6061铝合金局部塑性损伤。塑性损伤引起的静态分量源于材料中位错、晶粒等微观组织演化。而微裂纹调制生成静态分量的作用机制尚不明确，采用非线性兰姆波静态分量检测疲劳微裂纹还需进一步研究。

因此，本文采用非线性兰姆波静态分量技术，开展疲劳微裂纹的实验测量和仿真模拟研究，获得非线性参数随微裂纹长度的变化趋势，并分析不同模式基频兰姆波生成的静态分量对疲劳微裂纹的敏感性，实现了疲劳微裂纹的有效检测。

1 实验测量

1.1 试样制备

本文采用低周疲劳实验预制微裂纹。实验选用7075铝合金材料，加工为2 mm厚板状试样，如图1所示。在试样的中部切割三角形槽，作为疲劳微裂纹萌生源。使用Instron-8803液压伺服试验机在室温下对试样进行疲劳实验，采用应力控制模式，应力比为0.1，最大加载载荷为10 kN，加载波形为正弦波形，频率控制为5 Hz。通过控制循环加载周次，预制不同长度的疲劳微裂纹。使用光学显微镜观测疲劳微裂纹形貌，如图2所示。随着循环加载周次增加，疲劳微裂纹不断扩展，疲劳微裂纹长度迅速增大，各试样微裂纹长度如表1所示，而宽度和扩展方向无明显差异。

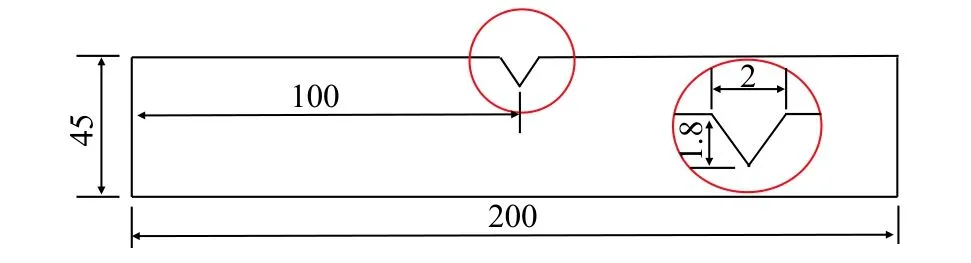
图1 平板试样（单位：mm）

图2 7075铝合金试样疲劳微裂纹形貌

表1 各试样微裂纹长度 mm

1.2 非线性超声实验测量

实验采用低频超声换能器间接测量获得非线性兰姆波静态分量。当低频超声换能器中心频率处于静态分量主瓣频率范围内时，可以有效接收静态分量信号[8]。实验测量系统由RAM SNAP 5000高能超声测量系统、激发和接收换能器、衰减器、放大器、数字示波器和计算机等组成，如图3所示。为了计算7075铝合金板状试样的频散曲线，首先采用脉冲回波法测量获得7075铝合金材料的纵波速度和横波速度，分别为6 257.99 m/s和3 064.60 m/s。本文选用群速度与静态分量近似匹配的S3模式兰姆波开展非线性超声兰姆波测量实验，如图4所示，激发频率为5 MHz。

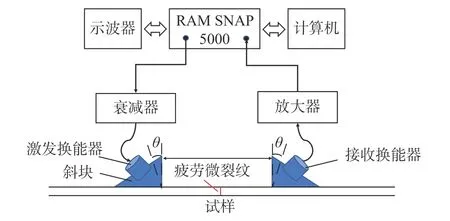
图3 实验测量系统示意图

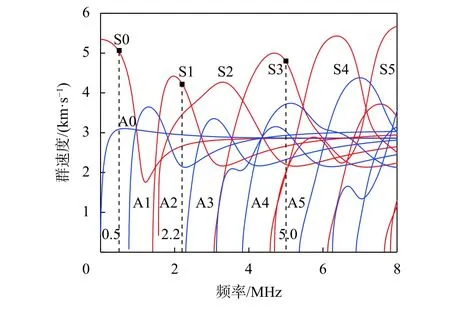
图4 7 075铝合金群速度频散曲线图

由RAM SNAP 5000系统产生10个周期的汉宁窗调制正弦脉冲激励信号，经衰减器加载到中心频率为5 MHz的压电换能器。根据Snell定律确定斜块角度为25°。采用中心频率为0.5 MHz的压电换能器接收静态分量，其中心频率处于静态分量主瓣频率范围内[10]。激发和接收换能器分别置于疲劳微裂纹两侧20 mm处。每个试样重复测量5次。对接收信号进行FFT处理，获得基频信号幅值A1和静态分量幅值A0。实验测量结果及分析见第3节。

2 模拟仿真

采用有限元软件Abaqus建立三维均质平板模型，如图5所示。模型上下端面和右端面设置为吸收边界。平板模型尺寸与实验试样一致。在平板中三角形槽顶端处设置微裂纹，裂纹面为硬接触、无摩擦。根据试样疲劳微裂纹形貌分析，设置微裂纹宽度为8 μm，长度如表1所示。材料属性设置为7075铝合金。

图5 含微裂纹三维平板示意图

为了保证模拟计算精度，设置单元尺寸小于λ/24，其中λ为基频兰姆波[4]。平板区域网格单元尺寸Δd1为0.5 mm。微裂纹处细化网格，网格单元尺寸Δd2为0.05 mm。平板网格采用三维C3D8R单元，吸收边界采用三维CIN3D8R单元。为了满足模拟计算的稳定性要求，时间增量步需要小于Δd/c，其中c为基频兰姆波和静态分量群速度的较大值。时间增量步为10–9s。

由于兰姆波具有多模式特性，为了分析单一模式兰姆波生成的静态分量，仿真模拟中激发低频S0模式兰姆波。在平板模型左端面施加均布位移信号，信号采用汉宁窗调制，中心频率为0.3 MHz，幅值为0.01 mm，周期为10周。在微裂纹右侧20 mm处的平板表面中间接收面内位移信号，如图5所示。对接收信号进行FFT处理，获得基频信号幅值A1和静态分量幅值A0。模拟仿真结果及分析见第3节。

3 结果与讨论

3.1 兰姆波静态分量分析

非线性超声测量实验中，接收到的时域信号如图6(a)所示。将时域信号在频率区间4.5～5.5 MHz和0～1 MHz进行数字滤波，分别获得基频兰姆波和静态分量的时域波形，如图6(b)～图6(c)所示。由于低频接收换能器的频响特性，接收信号的基频信号幅度稍小于静态分量。静态分量波包略长于基频信号，可能是由于群速度失配和兰姆波频散特性引起的。

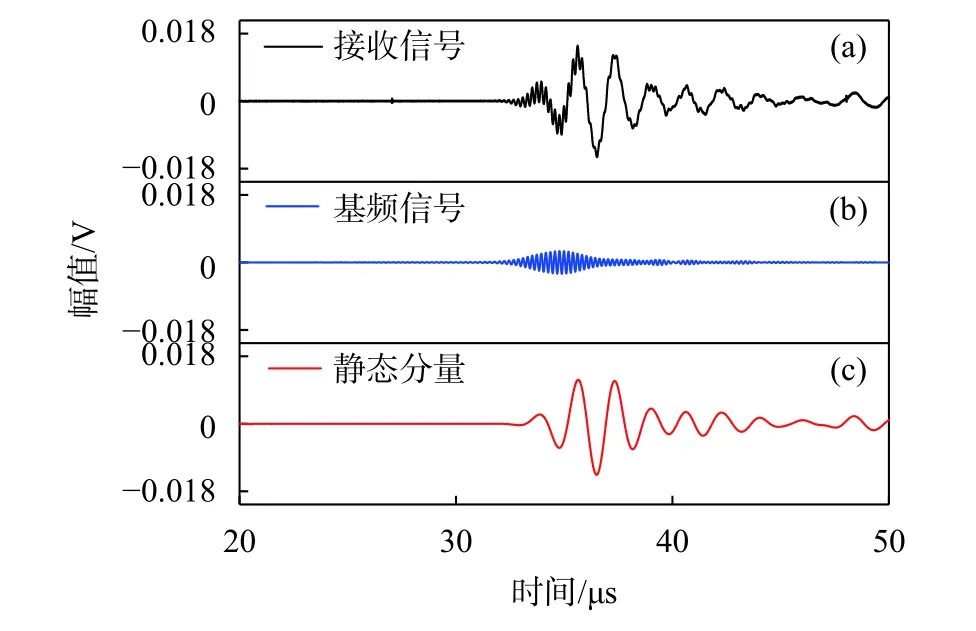
图6 实验中接收到的时域信号

为了验证基频兰姆波和静态分量的模式，分别测量基频兰姆波和静态分量的群速度。在激发换能器右端20～40 mm处，每间隔10 mm接收时域信号，如图7所示。对接收信号进行数字滤波，分别计算基频兰姆波和静态分量的群速度。基频兰姆波的群速度计算为4 803 m/s，与图3中5 MHz处S3模式兰姆波的群速度4 780 m/s基本一致。静态分量的群速度计算为5 170 m/s，与0.5 MHz处S0模式兰姆波群速度5 032 m/s基本一致。由此证明S3模式基频兰姆波可以有效产生S0模式静态分量。

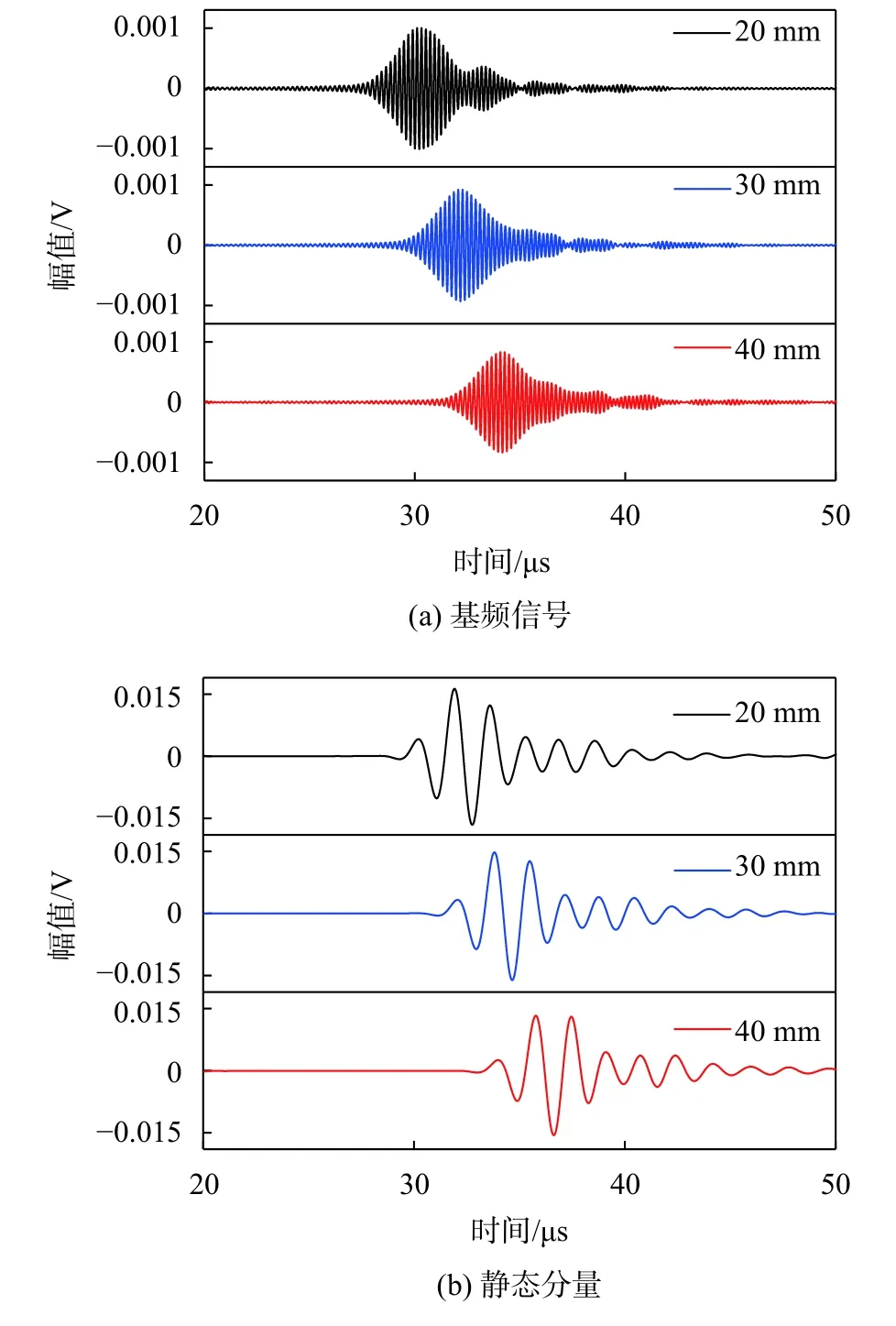
图7 不同传播距离时域信号

对图6(a)中20～46 μs的时域信号进行快速傅里叶变换（FFT）处理，分别获得基频兰姆波幅值A1及静态分量幅值A0，如图8所示。由于接收换能器的频响特性影响，基频兰姆波中心频率略微偏移，取峰值处幅值作为基频兰姆波幅值A1，计算微裂纹引起兰姆波静态分量的非线性参数A0/A1。

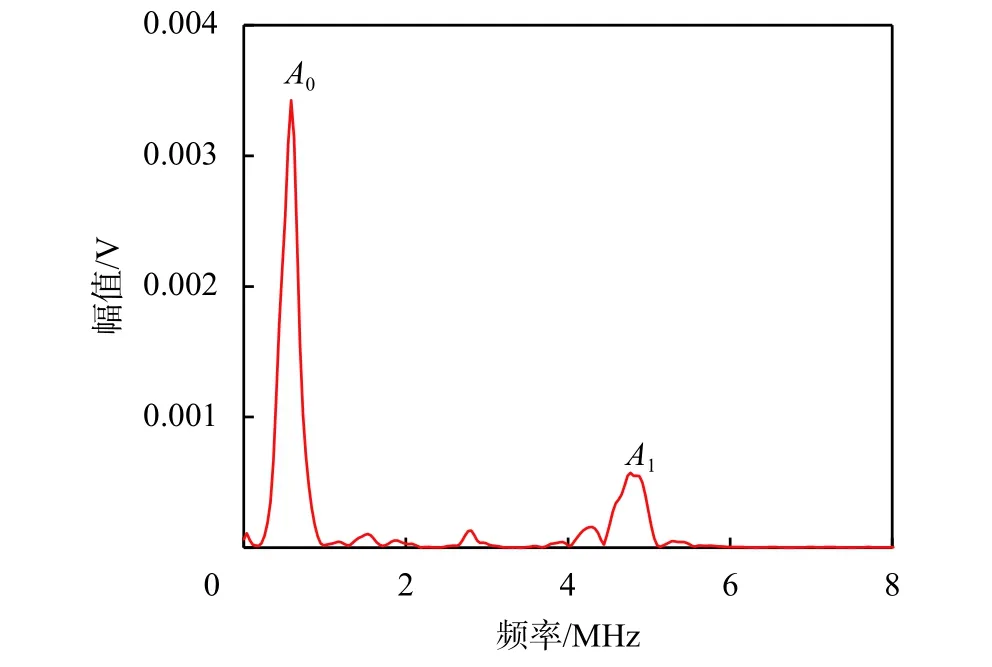
图8 接收信号频谱图

在仿真中，为了分析非线性兰姆波静态分量的生成机制，对无损平板和含微裂纹平板中接收到的信号进行对比分析。图9为兰姆波传播至微裂纹区域时的局部面内位移云图（面内位移U1），其中微裂纹长度为5.28 mm。从图中可以看出，微裂纹在基频兰姆波的拉伸和压缩作用下，分别处于张开和闭合状态。微裂纹界面的张开和闭合对基频兰姆波起到调制作用，从而引起静态分量的生成。

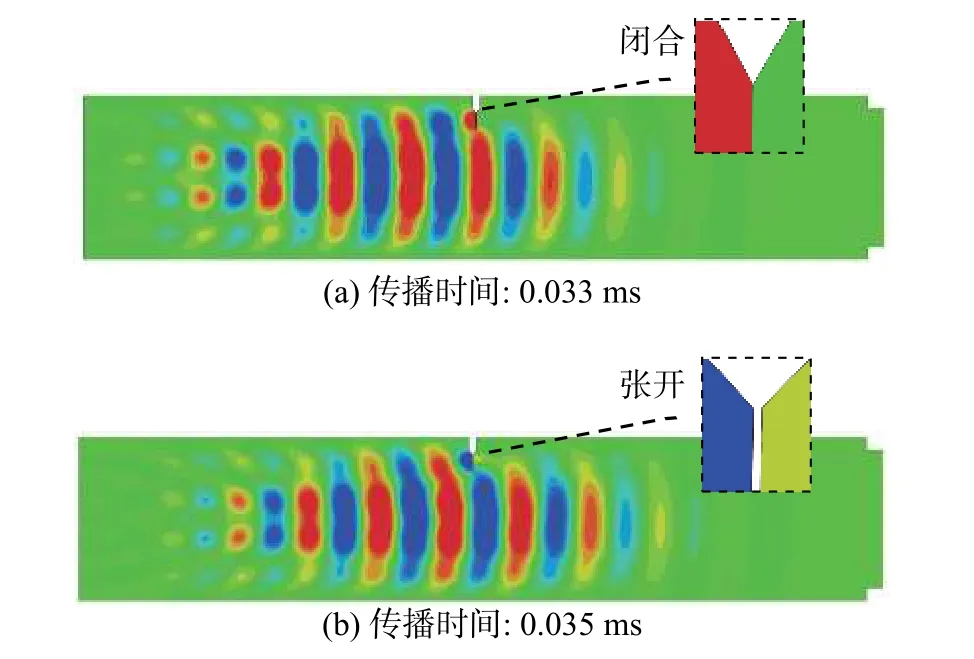
图9 兰姆波传播至微裂纹区域时的局部面内位移云图

图10(a)为无损板和含微裂纹平板时域信号，两者的时域信号仅存在微小的差异。模型设置吸收边界吸收了大部分反射信号，但不可避免地还存在一些微小反射信号。对0～62 μs的时域信号进行快速傅里叶（FFT）变换，分析生成的静态分量。如图10(b)所示，仅含微裂纹平板的接收信号中有明显的静态分量，证明微裂纹调制超声兰姆波可有效生成静态分量。从图10(b)中可以获得基频兰姆波幅值A1和静态分量幅值A0。

图10 无损平板和含微裂纹平板中的接收信号

3.2 疲劳微裂纹检测

实验中，对10个试样进行非线性超声测量，获得相对非线性参数A0/A1[4]，不同长度疲劳微裂纹生成静态分量相对非线性参数A0/A1的实验和模拟结果如图11所示。

由图11可知，实验和模拟得到的相对非线性参数A0/A1随微裂纹长度变化趋势基本一致。相对非线性参数A0/A1随微裂纹长度增加单调增加，且增长速率逐渐增大，表明静态分量对长裂纹更加敏感。这是由于随着微裂纹扩展，两裂纹面的接触面积增大，接触非线性效应增强，非线性参数快速增大。实验和模拟结果表明非线性兰姆波静态分量可以有效表征金属平板中的微裂纹。

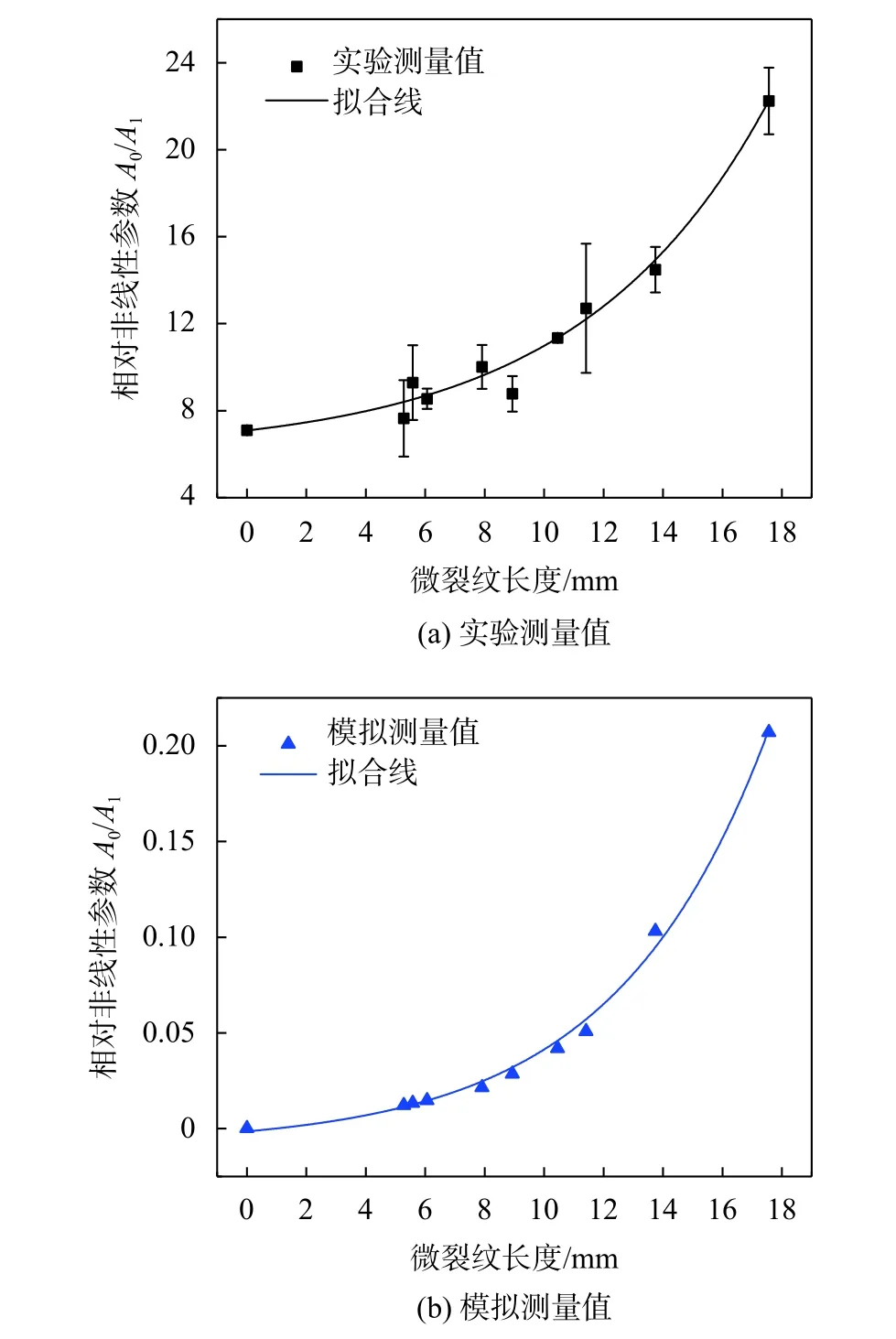
图11 相对非线性参数A0/A1与微裂纹长度关系

3.3 敏感性分析

为了进一步分析不同模式基频兰姆波生成静态分量对微裂纹的敏感性，另外选择频率为2.2 MHz的S1模式兰姆波（图4），对含疲劳微裂纹金属平板试样进行非线性超声测量。激发探头选用中心频率为2.25 MHz压电换能器，激发信号频率为2.2 MHz。根据Snell定律计算斜块角度为27°，其余实验参数均与第1.2节一致。将S1和S3模式基频兰姆波的相对非线性参数A0/A1进行归一化处理（图12）。

图12 归一化相对非线性参数A0/A1与微裂纹长度关系

由图12可知，两组基频兰姆波模式测量获得的相对非线性参数A0/A1随微裂纹变化的规律一致。S3和S1模式基频兰姆波的相对非线性参数A0/A1分别增长到313%和201%，S3模式基频兰姆波相对非线性参数A0/A1增长率约为S1模式基频兰姆波的1.5倍，表明S3模式基频兰姆波对微裂纹产生更强的调制作用，生成的静态分量信号对微裂纹更加敏感。

4 结束语

本文通过实验测量和数值模拟方法对铝合金平板中疲劳微裂纹引起的非线性兰姆波静态分量展开研究，获得主要结论如下：

1）通过对疲劳微裂纹引起的非线性兰姆波信号进行时域和频域分析，验证了疲劳微裂纹对基频兰姆波的调制作用及静态分量的生成。

2）非线性兰姆波静态分量相对非线性参数A0/A1随微裂纹长度单调增加，且增长速率随微裂长度增加而增加，非线性兰姆波静态分量可以有效检测金属平板中的疲劳微裂纹。

3）S3模式基频兰姆波生成静态分量的相对非线性参数A0/A1增长率约为S1模式基频兰姆波的1.5倍，S3模式基频兰姆波生成的静态分量对疲劳微裂纹更加敏感。