道岔对高速列车小幅蛇行极限环演变的影响

杨宜坤， 宁 静,2， 李艳萍， 陈春俊， 张 兵

(1.西南交通大学机械工程学院，四川 成都 610031; 2.轨道交通运维技术与装备四川省重点实验室，四川 成都 610031;3.西南交通大学 牵引动力国家重点实验室，四川 成都 610031)

0 引 言

轮对蛇行是轮对由于其对中特性在钢轨上产生的无法消除的横向振动[1]。当车辆系统的蛇行振动引起系统共振，演变为等幅稳态振动的极限环，此时速度为车辆系统的非线性临界速度[2]。车辆故障将使得非线性临界速度降低，使得原本正常运行的车辆产生大幅极限环震荡，即蛇行失稳[3]。国内某线路CRH380A高速列车出现异常小幅蛇行振动[4]，在车辆过道岔时演变为蛇行失稳，经查明该车存在二系横向减振器的故障。由True[5]发现在非线性与线性临界速度之间，车辆系统存在不稳定小幅与稳定大幅两种极限环，极限环的演变受外部激励影响，这是该车辆受道岔激扰产生极限环演变的理论依据。该车辆小幅蛇行时，其构架上的加速度测点信号幅值处于2～8 m/s2，低于GB/T 5599—2019标准中的蛇行失稳判别阈值，无法报警。王晓东等[6]对该信号进行了分析这种小幅蛇行的收敛与发散两种趋势，如图1(b)、(c)所示，并基于神经网络给出了这几种小幅蛇行演变信号的分类方法。

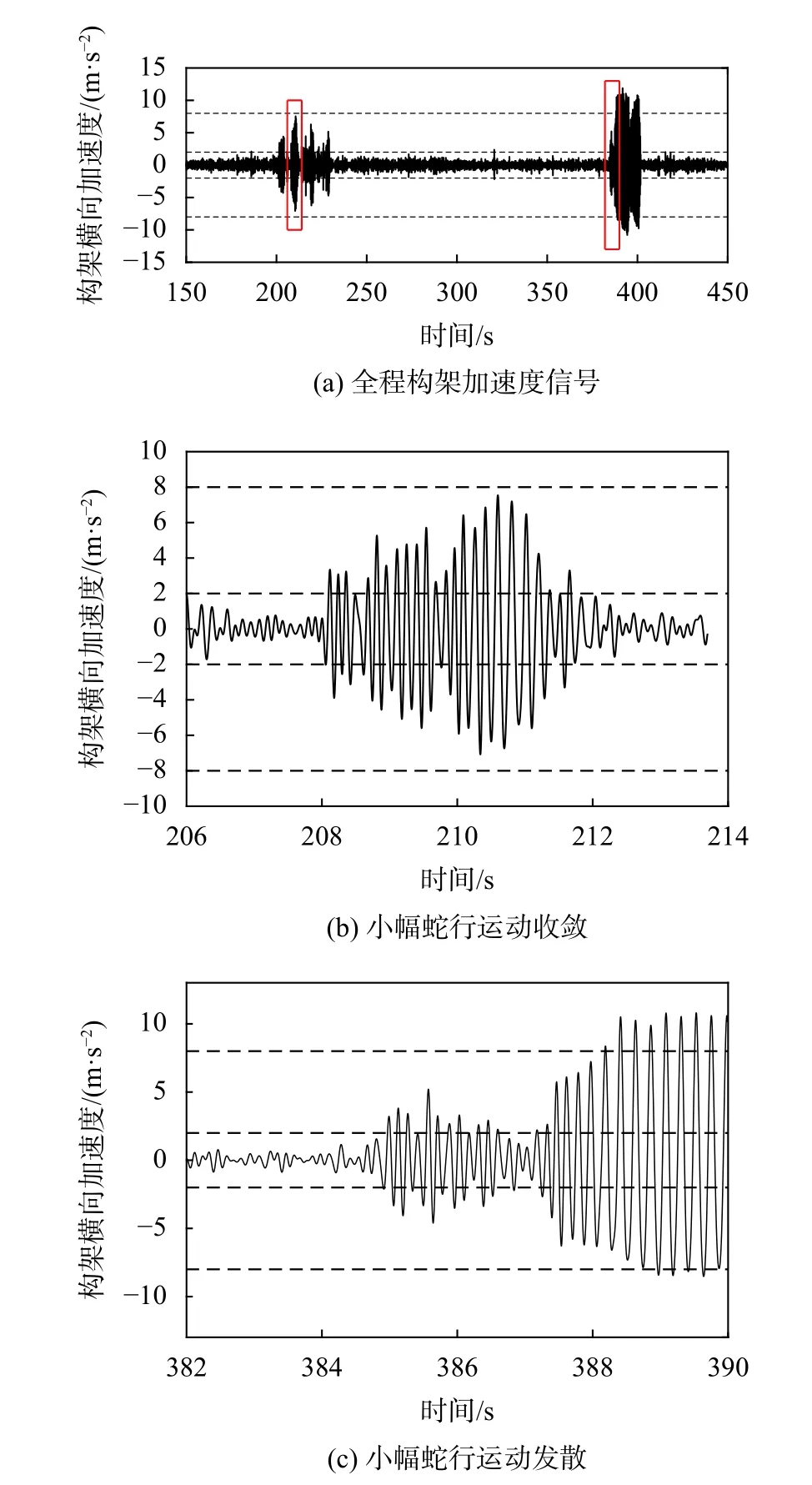
图1 异常蛇行车辆构架横向加速度信号[6]

翟婉明等[7]基于车辆仿真软件研究车辆过岔时的安全性，确定了列车过岔仿真研究的基本方法，但现有的高速列车横向稳定性监测标准，仅能在车辆已经蛇行失稳后报警，无法在小幅蛇行的演变条件下报警。对此宋欣武[8]提出了基于轮对横向位移的LMP监测报警方法，计算蛇行时的轮对横移量并设置阈值报警。Zeng等[9]基于列车在蛇行状态下部件振动的周期性，提出了周期性特征分析的报警诊断方法。上述研究提出的监测方法能够对普通路段上的小幅蛇行进行报警，推进了蛇行监测，但忽略了常见的道岔瞬时激扰的影响。目前仍缺少对于整车系统的小幅蛇行在岔区的演变机理研究。对此陈杨等[10]初步研究了道岔等效激扰对单转向架模型小幅蛇行状态的影响。但道岔除了等效轨道激扰外，其多点接触对轮轨关系存在进一步的影响。而这种影响是如何作用于小幅蛇行极限环的演变过程的尚不明确，且为还原故障车辆工况，应当建立整车模型，并从极限环角度深入研究小幅蛇行过岔演变机理。

赵飞等[11]研究了SIMPACK仿真软件对于车辆系统的简化的影响，且通过SVM分类准确率证明了仿真数据应用于横向稳定性研究的有效性。本文使用SIMPACK动力学仿真软件建立含减振器故障的CRH380A车辆动力学模型。并基于国内18号高速可动心轨道岔数据，引入完整的道岔模型至动力学模型，考虑岔区的轮轨多点接触。本文实验通过分别设置基于实测轨道的不同激扰路段，进行车辆系统极限环的计算，比较岔区的普通轨道、转辙区、辙叉区、完整道岔4种激扰的分别作用下，车辆临界速度以及小幅蛇行不稳定极限环的演变。通过设置列车进入岔区时轮对不同幅值的初始横移量，模拟列车进岔时的不同初始小幅蛇行幅值对车辆系统极限环演变的影响。本文对首次对小幅蛇行过岔时极限环的演变机理进行研究，通过机理研究希望能够为蛇行监测在过岔方面的改进。

1 车辆-道岔系统动力学模型

1.1 车辆系统动力学模型

基于异常蛇行振动的CRH380A高速列车的实际参数建立的车辆动力学模型遵循图2所示的车辆系统拓扑结构。该拓扑结构包含1个车体c，2个转向架b构架，4个轮对w，这些部件均被视为刚体并考虑以下6个自由度：纵向x、横向y、垂向z、侧滚φ、点头β与摇头ψ。其中车体和构架之间由二系悬挂系统s连接，该系统包含空气弹簧、横向减振器、抗蛇行减振器、牵引拉杆、横向止挡。构架与轮对之间通过一系悬挂系统p连接，其包含轴箱弹簧、垂向减振器、转臂式轴箱定位装置。上述拓扑结构充分考虑了影响车辆动力学特征的所有部件，构成了完整的车辆系统模型。根据模型的共42个自由度，得出42个运动方程。将其用矩阵形式表达，即得到车辆系统的动力学方程组如下式：

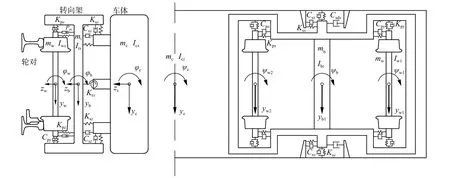
图2 车辆系统拓扑结构

式中：{y}——向量组代表所有部件的位移；

{}与 {}——向量组则对应了各部件（角）速度与（角）加速度；

[M]——由车辆系统各部件的质量与转动惯量组成的 42 × 42的矩阵；

[C]与 [K]——42 × 42矩阵，包含了系统内的阻尼器参数与弹簧部件的刚度；

{F}——由部件间的力与转矩的算式组成的向量组。

通过对式（1）在时间尺度上迭代求解，即完成车辆系统在路轨上的运行仿真。

1.2 岔区轮轨接触关系计算

在轮轨相互关系的蠕滑力计算中，对于岔区的大批量轮轨关系数据的计算处理，当轮对的自旋蠕滑力较大时[12]，与CONTACT模型数据最接近的是FASTSIM[13]算法。车辆LMA踏面在转辙区与辙叉区的对应的轮轨接触几何如图3所示。在转辙区与辙叉区尖端处求解多点接触时，首先对轮轨接触几何求导，判断可能存在的其他接触点。再根据接触点的数据进行比较，确保接触点相互独立，不会处于同一个接触斑[14]。随后对多个接触斑分别计算轮轨间的蠕滑力，随后求各接触点的合力修正式（1）中的 {F}的计算结果。列车侧向过岔时的限速为100 km/h以下，无法产生小幅蛇行状态，本文仅针对某线路CRH380A高速列车以较高的速度直向通过18号可动心轨提速道岔的工况进行研究。因此不存在护轨对轮背的冲击以及尖轨在转辙作用时对轮缘的冲击。除此之外本文仅研究岔区轮轨接触带来的激扰对小幅蛇行极限环演变的影响，所以采用道岔型面插值的方式建立道岔模型，并将道岔视为刚体。

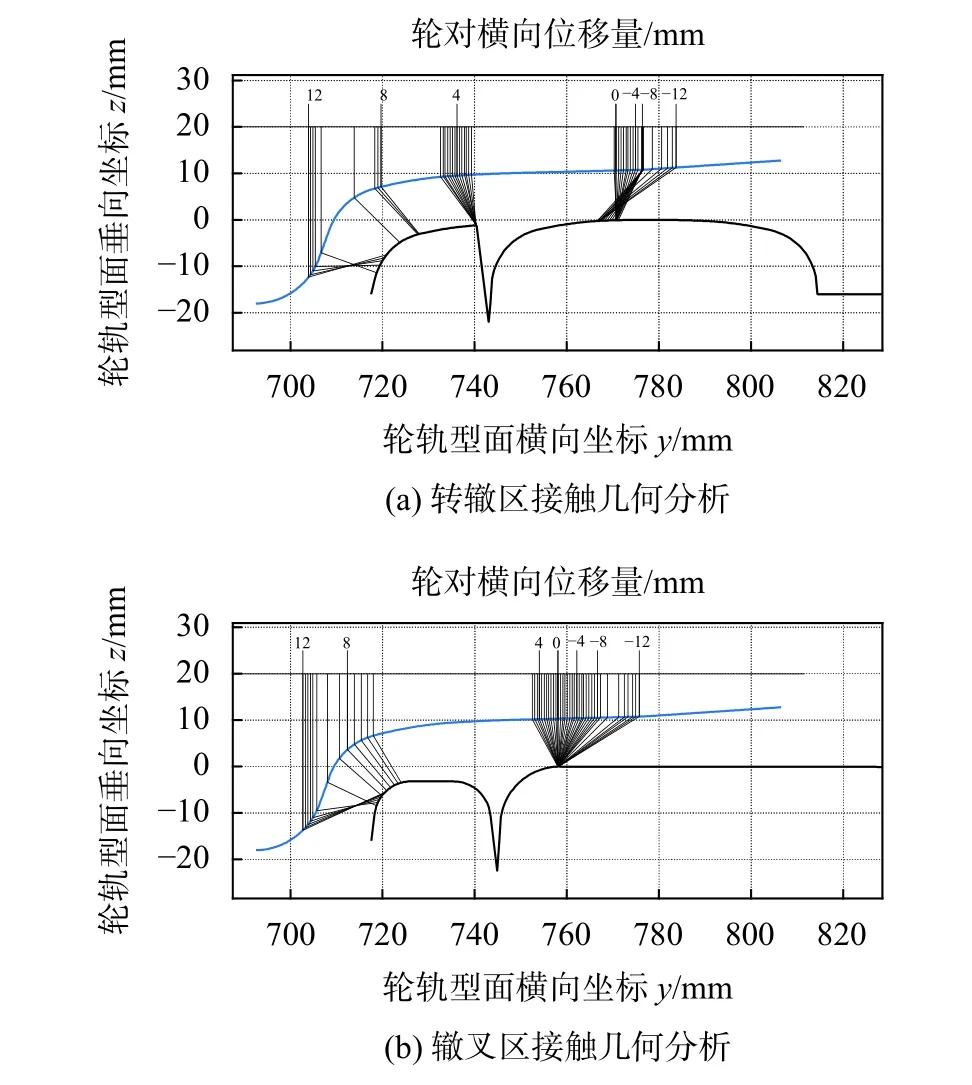
图3 道岔区的轮轨接触几何随轮对横移量变化

2 故障车辆蛇行模型验证

2.1 二系横向减振器故障分岔验证

CRH380A车辆服从亚临界Hopf分岔类型，轨道型面为CN60/kg钢轨截面。使用降速法分析车辆系统极限环，由此计算该模型标准工况下的非线性临界速度为405 km/h，如图4所示。高于该速度时，车辆系统充分激振会处于约为9.5 mm幅值的等幅震荡极限环。在低于该速度行驶时，蛇行运动收敛，不会出现小幅蛇行发散的蛇行失稳。随后使用Roci Loci法计算线性临界速度，为641 km/h。当车辆运行速度处于非线性临界速度与线性临界速度之间时，车辆可能产生不稳定的小幅极限环，表现为构架监测的加速度幅值低的小幅蛇行运动，也可能演变产生稳定的大幅极限环运动，表现为蛇行失稳，也可能演变为小幅蛇行收敛，这符合亚临界分岔的车辆系统的蛇行运动特征。验证了模型的分岔准确性。

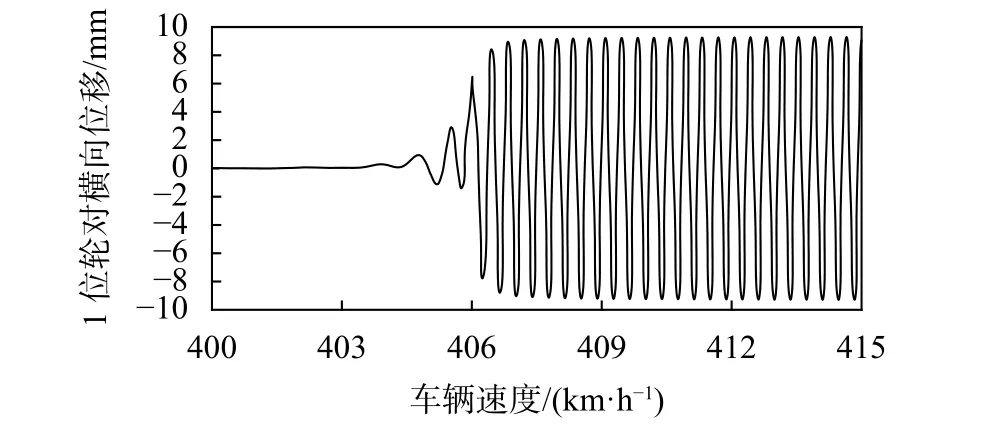
图4 无故障车辆的降速法极限环计算

为了模拟二系横向减振器故障对车辆运行的影响，本文调整二系横向油压减振器的阻尼特性为10%。随后同样进行上述计算，如图5所示。故障车辆在从105 km/h至235 km/h的速度区间内，会在光滑平直轨道上产生约5 mm幅值的稳定的极限环。当列车处于235 km/h至390 km/h速度下时，车辆不能在理想的光滑平直轨道上形成稳定的极限环幅值。当速度处于390 km/h时，极限环跃变至9.5 mm。这说明当二系横向减振器被破坏之后，故障车辆服从于一种复杂的分岔状态，类似于多个亚临界分岔的组合。

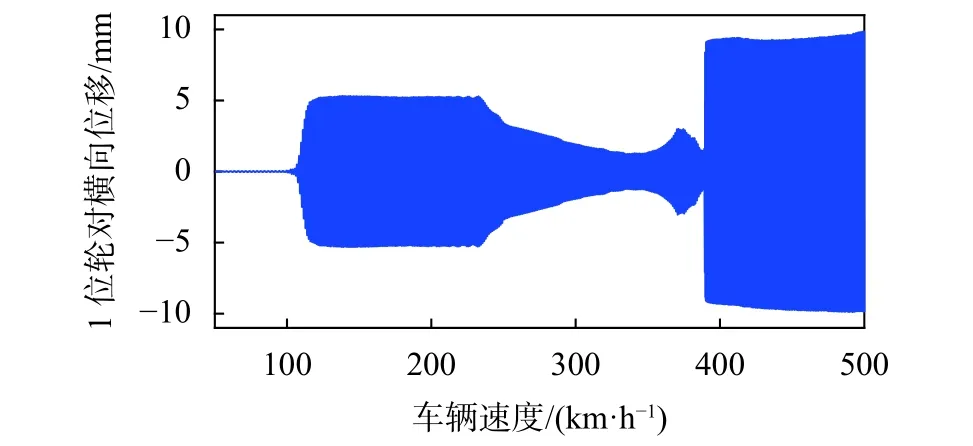
图5 故障车辆的降速法极限环计算

2.2 故障车辆过岔蛇行振动信号验证

再对车辆-道岔仿真模型的横向振动加速度信号进行与实测数据对比的验证。首先基于该列车的运行路况引入对应的实测轨道激励、线路曲线以及道岔组，使用标准与故障的车辆模型进行仿真，对比构架测点的横向加速度数据。图6可以看出在正常车辆的实际运行情况下，在非岔区路段上加速度信号幅值低于2 m/s2，岔区产生小幅的2～8 m/s2振动后收敛，仿真车辆的信号与该特征一致。图7可以看出未更换故障减振器的车辆在非岔区路段上的加速度信号长时间处于2～8 m/s2的幅值区间，由于轨道不平顺激励作用，车辆处于不稳定极限环状态。当车辆进入道岔后，小幅蛇行演变为蛇行失稳。由图可知仿真模型的小幅蛇行演变特征与实际情况相同。

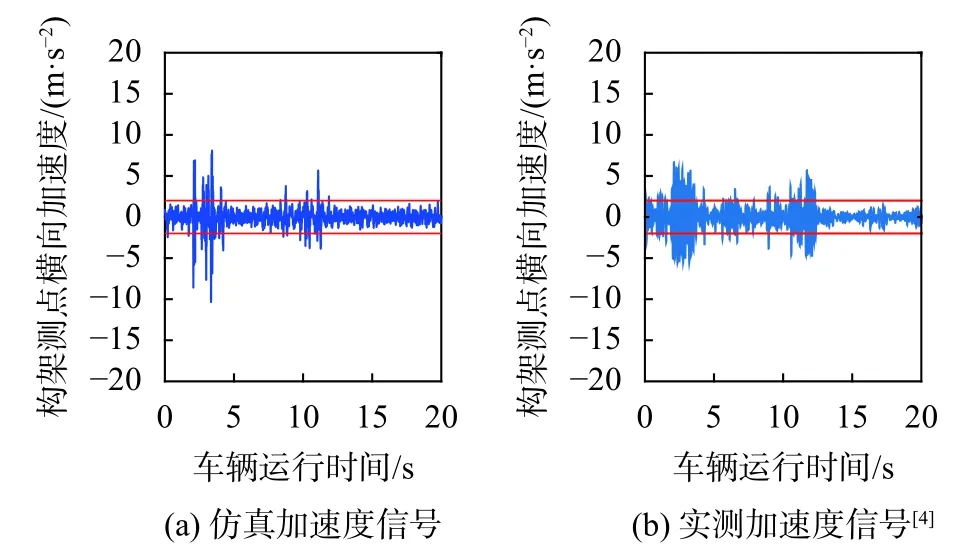
图6 正常车辆仿真与实测过岔信号对比

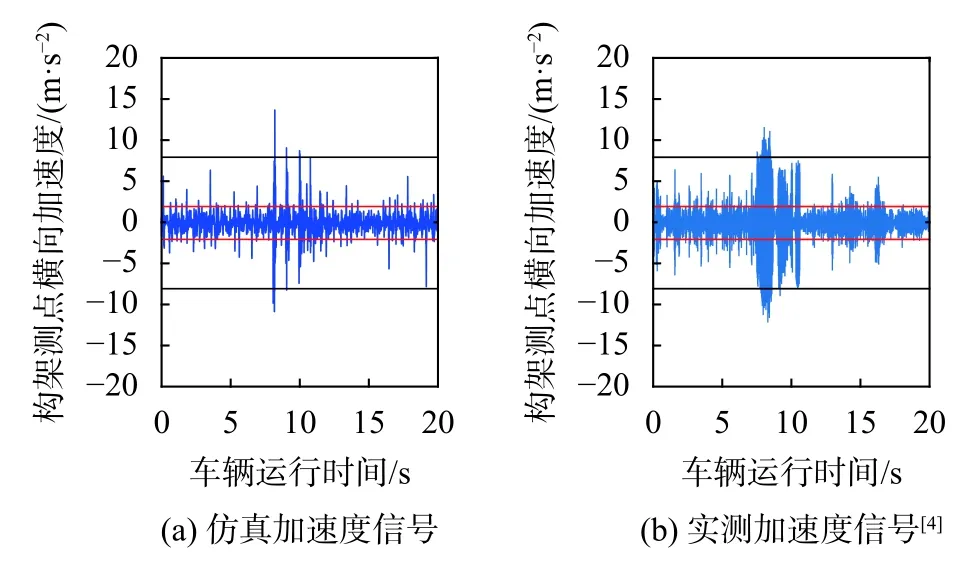
图7 故障车辆仿真与实测过岔信号时域对比

轮对振动频率范围，其上限为自由轮对的22 Hz，下限为刚性轮对的1 Hz[1]。分析该频段信号，由于列车横向振动信号为非平稳信号，故以2 s为步长将故障车辆的全程仿真与实测信号的小幅蛇行部分分割成18对样本进行对比验证。其中绘制一组样本的FFT频域图对比如图8。利用互信息分析计算18对信号样本中，仿真信号与实测信号的互信息MI均大于0.75，仿真信号对实测信号的还原程度达到计算要求。综上，本文建立的故障车辆过岔模型符合要求，在小幅蛇行与失稳演变上的横向稳定性能与实际故障车辆案例相近，可以用于小幅蛇行过岔演变机理的研究。

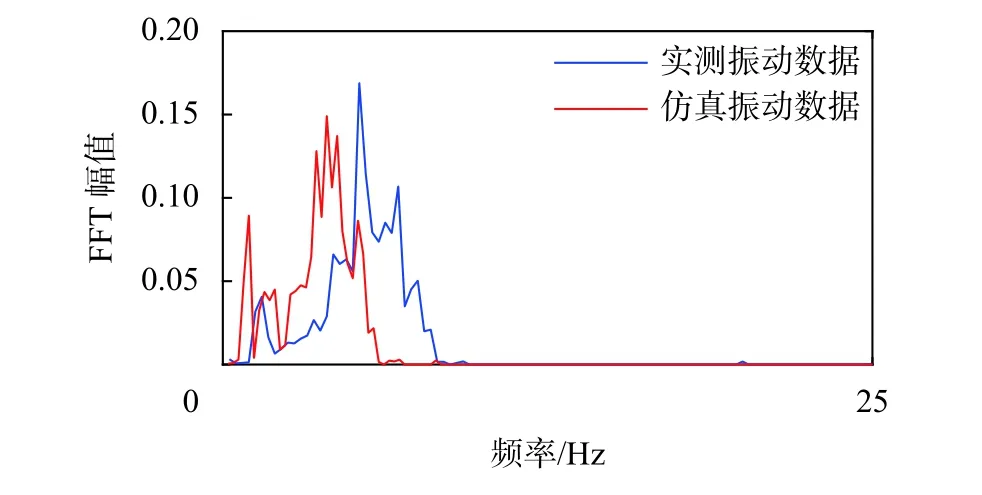
图8 故障车辆小幅蛇行信号仿真与实测频域对比

3 道岔对小幅蛇行极限环的影响

3.1 蛇行失稳临界速度分析

当车辆系统部件处于等幅极限环震荡时，以1位轮对的横移量可以对轮对蛇行运动的极限环进行表征[15]。首先，为了分析不同激扰下的车辆失稳临界速度，采用以下方法观测车辆系统的极限环特征：先设置一段含实测轨道不平顺激励的普通轨道，随后是一段待分析的激励轨道，分别设置普通轨道、转辙区、辙叉区及全道岔激励，最后接上一段足够长的理想光滑平直轨道。让列车匀速通过上述全部轨道，在第一段中使其被正常激振后，进入待分析轨道段使其受到激扰，在理想轨道上观察车辆系统在何种速度下产生稳定的极限环，此速度为该激扰条件下车辆系统的蛇行失稳临界速度。利用上述方法实验得到的结果如图9所示。在普通轨道、转辙区、辙叉区、完整道岔激扰下，故障车辆的蛇行失稳临界速度分别为205 km/h、187 km/h、173 km/h与166 km/h。对此结果进行分析可知，即使可动心轨道岔已消除有害空间，但其激扰仍将降低车辆的蛇行失稳临界速度。辙叉区的作用比转辙区更剧烈，这是因为转辙区尖轨曲率小于辙叉区长短心轨。在岔区的多点接触状态结束后，轮轨接触斑的跳变等效于一种瞬时、大幅的轨道横向不平顺，辙叉区产生的这种等效的不平顺更大。右开道岔作用于右轮，这种瞬时激扰使得车辆系统偏离平衡位置。

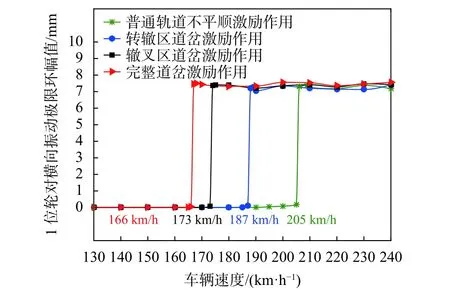
图9 不同激扰下车辆系统极限环计算

随后研究车辆在不同初始轮对横移量的小幅蛇行状态下通过道岔激扰的情况。轨道设置与上部分相同，第二段线路保持完整道岔激励不变，在车辆初始运行时调整1、2、3、4位轮对的初始横移量，模拟不同的轮对小幅蛇行运动幅值进入道岔后的情况。由于轮缘的对中作用，车辆极限环在高速情况下不会超过9.5 mm，低速情况下不超过8 mm。因此分别采取2 mm、4 mm、6 mm与8 mm的初始横移量进行仿真计算，得到的极限环计算结果如图10。为了便于比较普通轨道激励与道岔激励在重复上述实验下的不同表现，以及对比不同初始横移量下轮对蛇行运动产生稳定极限环的临界速度，得到的结果如表1所示。其中v0是普通轨道激励工况，vT是道岔激励工况。可以看出列车进入道岔前，若处于较大的初始轮对蛇行横移幅值，经道岔激扰后，车辆蛇行震荡产生稳定极限环的临界速度更低。由于小幅蛇行幅值可能无法引起构架加速度信号报警，在进岔前减速可能无法使已处于较大不稳定极限环幅值的小幅蛇行状态的车辆演变为避免蛇行失稳。

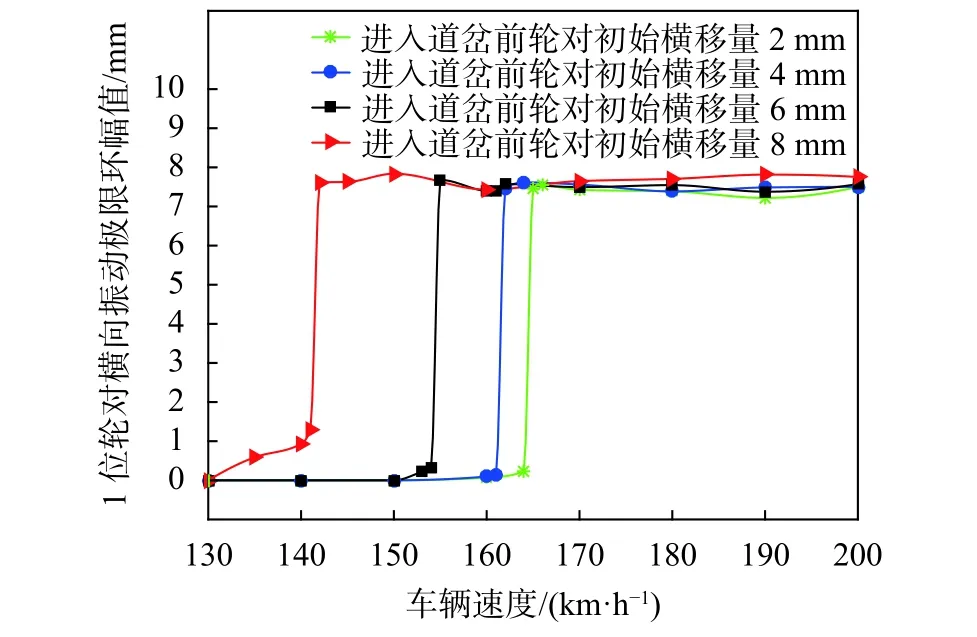
图10 不同轮对横移幅值进岔后的极限环计算

表1 不同条件下的蛇行失稳临界速度计算 km/h

3.2 基于相轨迹的极限环演变分析

基于上文的仿真实验，可以得到车辆系统经激扰后在理想轨道上的轮对横向振动的数据。将1位轮对横移量与横向振动速度构成相平面，对轮对横移的相轨迹进行分析，可以观察到轮对在出现大幅度极限环之前，在理想轨道上短暂出现了一个不稳定的极限环。当极限环发散时，不同条件下极限环演变状态不同。根据上一节可知，当进入道岔的初始轮对横移量小于4 mm时，它对车辆的临界速度影响很小。所以选取普通轨道产生的极限环数据为对照，再选取初始轮对横移量为0，4 mm与8 mm的轮对横向运动的数据绘制相轨迹图如图11所示。

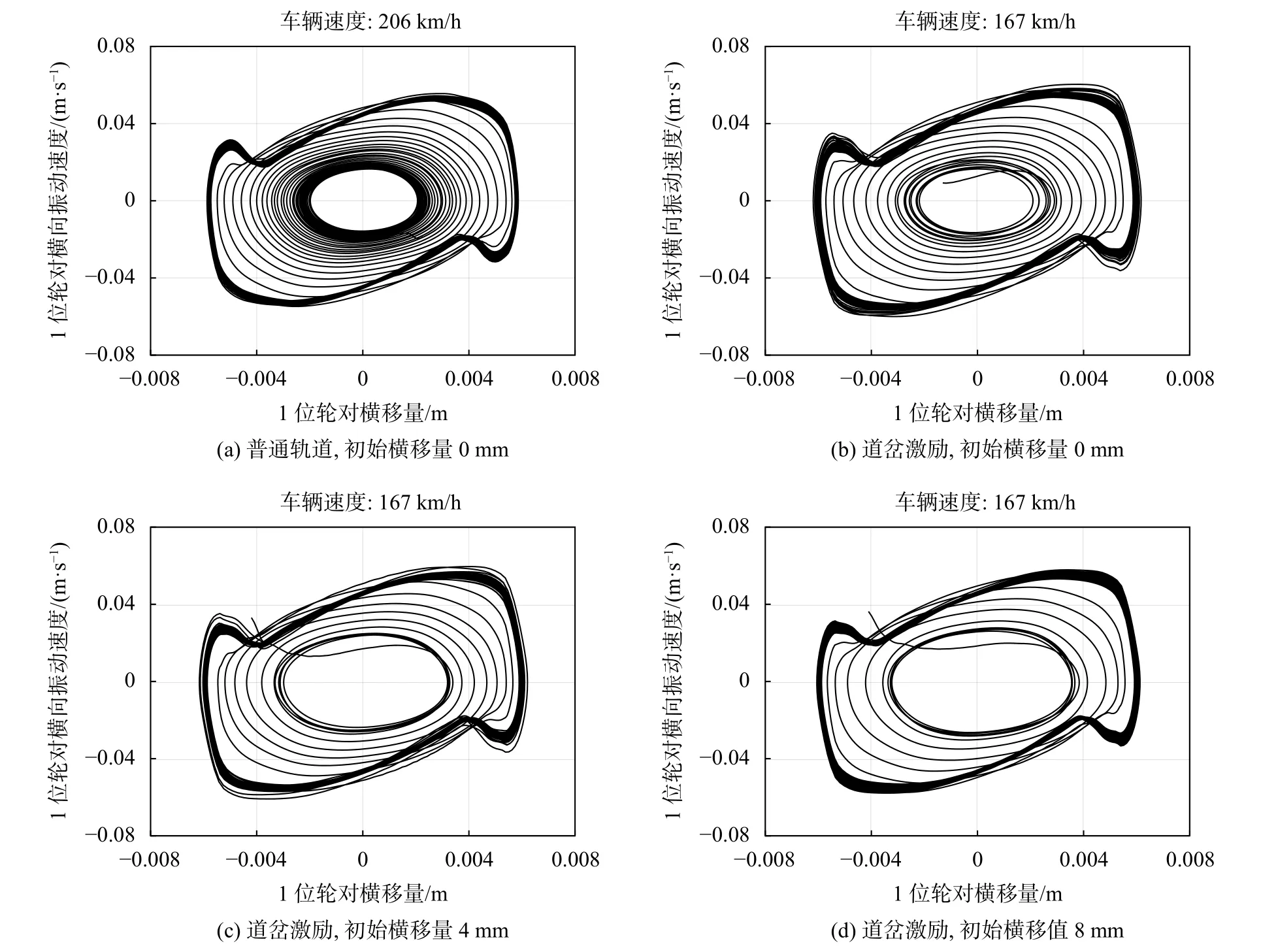
图11 故障车辆系统极限环的相轨迹图

对于图11，首先对比图(a)与图(b)，轮对在道岔上出现小幅蛇行的不稳定极限环发散为稳定的大幅值极限环的临界速度更低，演变速度更快。通过对比不同初始轮对横移量进岔时的轮对横移相轨迹图(b)、(c)、(d)可以发现，在相同速度下，轮对初始横移量越大，轮对相轨迹在相平面内发散为蛇行失稳运动的速度越快，不稳定极限环转变得也更快。

4 结束语

本文根据实际的故障车辆以小幅蛇行状态下通过道岔时，小幅蛇行极限环发散为蛇行失稳稳定极限环的现象，建立了相符的故障车辆过岔模型。本文对极限环的演变受道岔激励的影响与小幅蛇行自身的初始轮对横移幅值的影响进行了分析，得到了如下结论：

1）二系横向减振器的失效，将使服从亚临界分岔的车辆在较低速度下运行出现受激励影响的不稳定的极限环。道岔对车辆系统的激扰相比普通路轨激扰将降低车辆系统产生稳定震荡的极限环的临界速度，从而使得故障车辆在低速下由小幅蛇行演变为蛇行失稳，仿真表征为小幅不稳定极限环演变为大幅稳定极限环。

2）道岔的固有结构影响了道岔区的轮轨关系，从而在列车过岔时，产生较大的横向外部激励，使得在道岔激扰下车辆系统蛇行失稳临界速度更低，极限环演变得更快。同时进岔前车辆小幅蛇行振动幅值的增加同样会降低车辆蛇行失稳临界速度，提高极限环演变速度。所以在车辆在线监测中，应当对根据轮对进道岔之前的小幅蛇行运动特征而相应地进一步降低进岔速度。

3）本文的仿真分析仅考虑进岔前车辆蛇行的横移量影响。由于在线监测存在延时，监测到的小幅蛇行状态可能会在进岔前进一步演变，且蛇行状态除了横移量外还有初始横移加速度与横移速度等条件影响，所以故障车辆在进岔时的速度应当根据小幅蛇行状态监测结果进一步降低。除此之外，可以在后续研究中引入车-岔柔性体耦合振动分析及轮轨动态磨耗模型的分析。