地面简谐运动作用下双自由度体系鞭梢效应的影响因素研究

李明瑧,郭长青

(1.南华大学 土木工程学院,湖南 衡阳 421001;2.南华大学 数理学院,湖南 衡阳 421001)

0 引 言

质量和刚度在竖直方向上变化很大的建筑结构，在地震作用下可能发生鞭梢效应，造成严重的后果，因此鞭梢效应受到了广泛的关注和研究。

钟万勰和林家浩[1]是国内最早开始进行建筑鞭梢效应研究的学者，他们从耦合振子的动力特性出发，建立一个双质点模型，用逐步积分法，指出增大顶部突出部分的刚度不一定有利于减小鞭梢效应，应在设计阶段通过动力计算来检验结构是否容易产生鞭梢效应，并按计算结果来调整结构的刚度或质量分布。武际可[2]以鞭子为例谈到了鞭梢效应，指出发生鞭梢效应的原因在于，鞭梢部分的移动速度远大于主体部分。刘铁林[3]对双自由度无阻尼体系进行了动力计算，指出当突出物的固有频率接近主体结构的固有频率，且其质量远小于主体结构的质量时，是该突出部分的结构受震害破坏的原因之一，在设计时应给予注意，并指出建筑物的突出部分虽然自身容易受震害破坏，但它对主体结构有一定的保护作用。阎石等[4]研究了仅考虑剪切变形时的双自由度无阻尼体系的自由振动和双自由度体系在主体结构上受一个简谐荷载时的受迫振动，指出当建筑物上部突出部分的质量和刚度远小于主体结构的质量和刚度，且其固有频率与主体结构固有频率相接近时，突出部分的振动反应最为强烈。赵永生和贾栗[5]研究了在地面位移为简谐荷载的情况下，在只考虑地面运动的卓越频率的情况下，得出当上下两部分的自振频率接近且与地面卓越频率相近时，鞭梢效应最为强烈，当上下两部分自振频率比值趋向于0或无穷大时，鞭梢效应减弱或消失。曲淑英等[6]通过研究多自由度无阻尼体系在地面运动为简谐荷载的受迫振动，指出当突出物某一自振频率与整体结构的固有频率相同且与地面运动扰频相近时，结构最易发生鞭梢效应。郑以微和彭德喜[7]通过研究高层建筑在强风作用下的鞭梢效应，指出鞭梢效应的强弱跟突出部分和主体部分的固有频率比值有密切关系，当其比值接近于1，并与强风卓越频率接近时，最易发生鞭梢效应。近几年的动力鞭梢效应研究主要以通用有限元软件建模设计分析为主，且理论分析多采用无阻尼模型。G.Chen[8]对无阻尼多自由度系统进行研究分析其自振频率与鞭梢效应的关系，结果表明，突出物的自振频率影响着鞭梢效应的强弱，当突出物的自振频率和主体频率相近时，突出物的鞭梢效益最为明显。Y.Su和E.L.Liu[9]采用有限离散单元法对冰川在地震作用下的动力鞭梢效应进行分析。文献[10-13]以实际工程建筑为例建立有限元模型进行分析，分别对进水塔排架、吸热塔、超高扬程升船机顶部机房、某水电站进水塔、混合结构吸热塔、高耸钢结构电视塔进行抗震和鞭梢效应分析，结果表明，当突出物和主体结构的质量与刚度差异较大时，鞭梢效应对主体结构动力响应影响较小。

尽管诸多学者对结构的鞭梢效应机理进行了一定的分析，但是并未对众多影响因素进行深入的研究。本文以双自由度体系的上部结构与下部结构绝对位移的振幅比作为鞭梢效应的表征量，系统研究了外激励频率与上部结构自振频率之比、上部结构与下部结构的质量比和刚度比、结构阻尼比四种参数对其的影响。

1 无阻尼体系受迫振动分析

图1所示为双自由度无阻尼体系的计算简图。

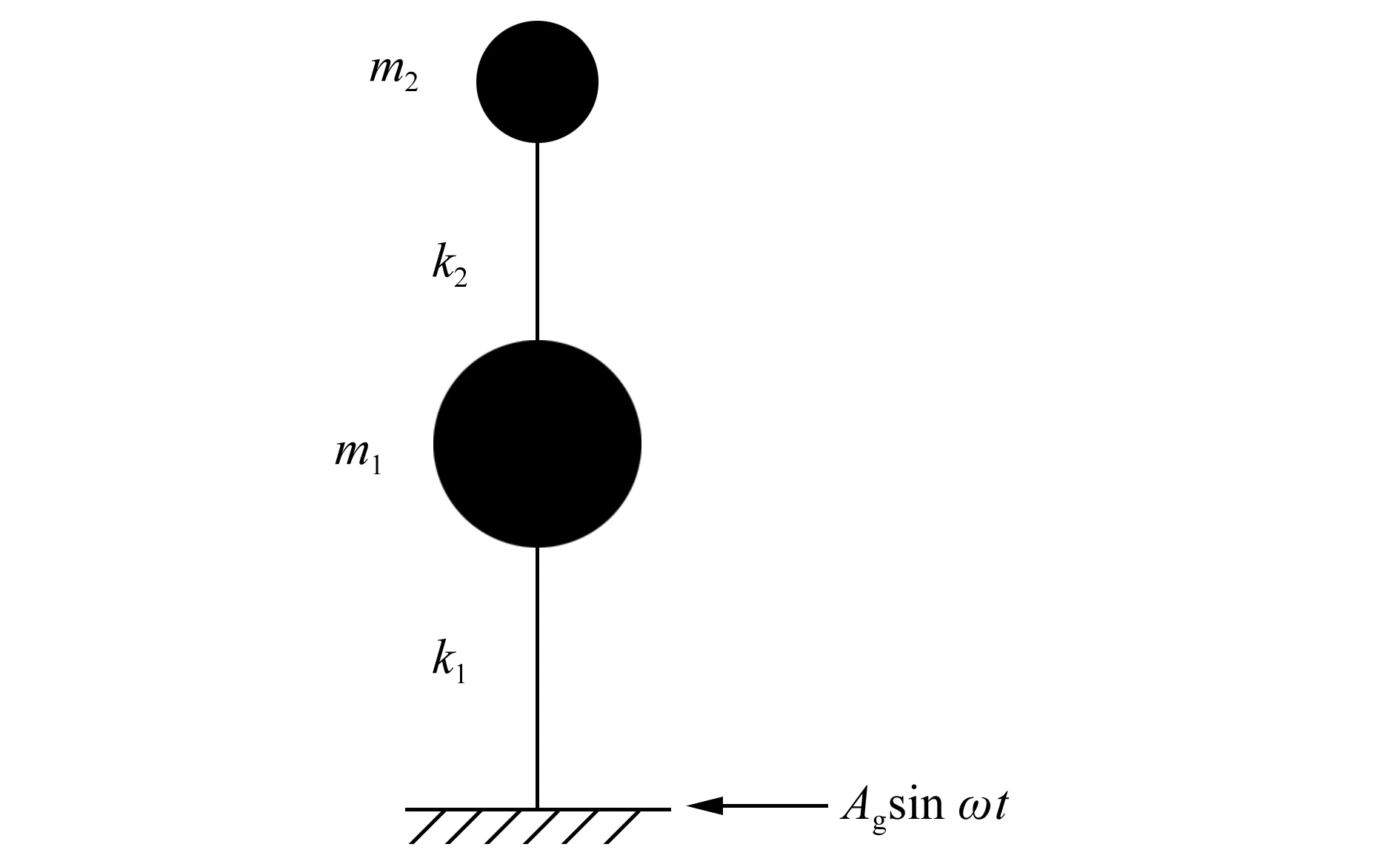
图1 结构计算简图Fig.1 Structural calculation sketch

体系在地面简谐运动作用下的运动方程为：

(1)

其中m1，m2分别为下部结构与上部结构的质量，k1，k2分别为它们的刚度。x1a、x2a分别为它们的绝对位移，xg为地面简谐运动位移：

xg=Agsinωt

(2)

方程(1)左右两边同时除以上部结构的质量m2：

(3)

引入无量纲量质量比cm和刚度比ck：

(4)

及下部结构和上部结构各自的自振频率：

(5)

将式(4)、式(5)代入式(3)得：

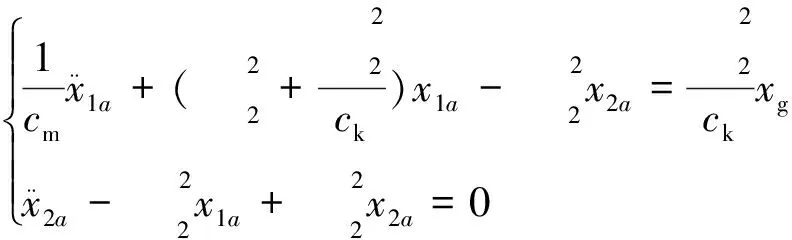
(6)

假设：

(7)

将式(7)代入式(6)经计算可得：

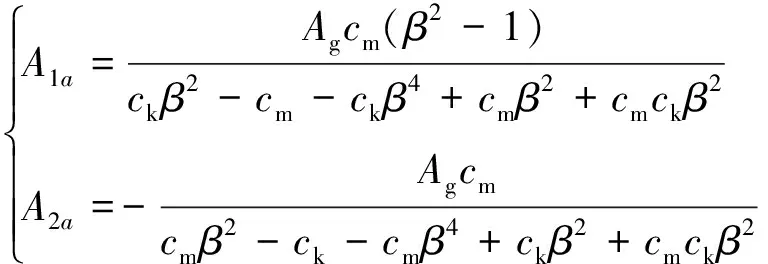
(8)

其中：

上部结构与下部结构的绝对位移振幅的比值：

(9)

由式(8)、式(9)可知，A1a、A2a与质量比、刚度比和频率比三者都有关，但它们的比值A2a/A1a仅与频率比β有关；当β→1时，A2a/A1a→∞，结构发生剧烈的鞭梢效应。

值得注意的是：式(8)与上部结构作为单自由度体系在简谐荷载作用下的动力放大系数公式在形式上完全相同，但有一个重要的不同点：当β=1时，A2a是有限的，导致A2a/A1a→∞的原因是A1a→0，这是一个很奇特的现象：下部结构自身不动，只在地面与上部结构之间起传递力的作用！可利用该现象对下部结构进行被动隔振。

2 有阻尼体系受迫振动分析

图2所示为双自由度有阻尼体系的计算简图。

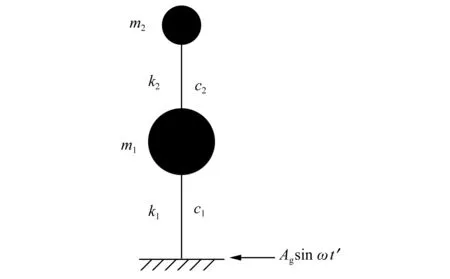
图2 结构计算简图Fig.2 Structural calculation sketch

为了便于对阻尼矩阵进行对角化处理，对有阻尼体系的分析先从相对运动入手，最后再叠加上地面运动求出结构的绝对位移。

结构在地面简谐运动作用下的受迫振动方程为：

(10)

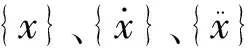
假设[φ]为双自由度无阻尼体系自由振动时的振型矩阵，令{x}=[φ]{q},代入式(10)得：

(11)

式(11)左乘[φ]T得：

(12)

其中：

振型矩阵取为：

(13)

结构的两阶自振频率与上部结构自振频率的比值分别为：

(14)

假设结构的阻尼矩阵可对角化：

(15)

则式(12)可转化为：

(16)

其中：

则：

(17)

其中ζn为结构的振型阻尼比。

假设：

qn(t)=Cnsinωt+Dncosωt

(18)

代入式(16)经计算可得：

(19)

其中：

再由{x}=[φ]{q}求得结构的相对运动位移为：

(20)

结构的绝对位移为：

(21)

最终结可表示为：

(22)

其中：

3 有阻尼体系幅频特性分析

图3为刚度比等于0.1，质量比取不同值时的结构幅频特性曲线。图4为质量比等于0.1，刚度比取不同值时的结构幅频特性曲线。图5为质量比和刚度比相等且同步变化时的结构幅频特性曲线。

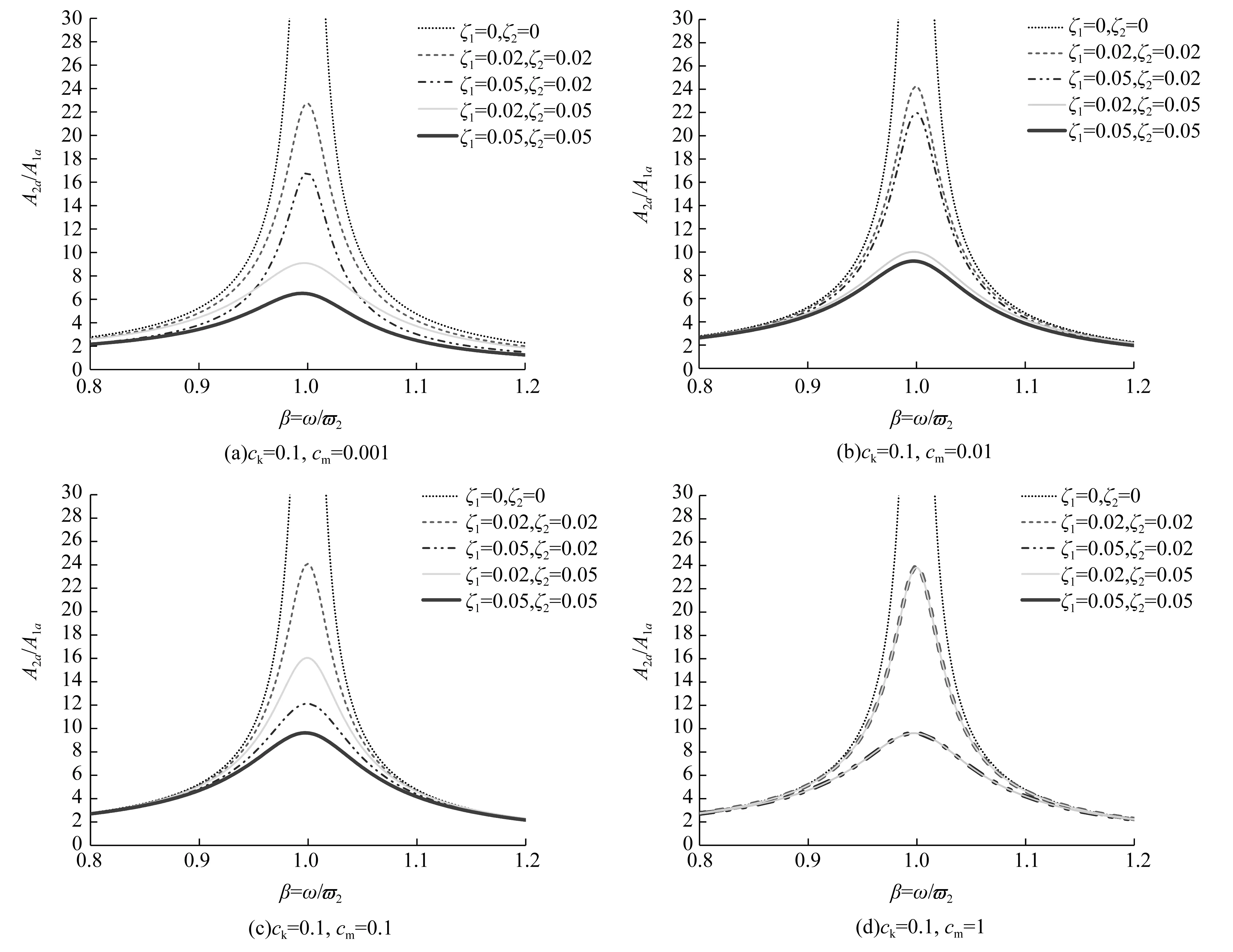
图3 相同刚度比不同质量比的幅频特性曲线(刚度比为0.1)Fig.3 Amplitude-frequency characteristic curve with the same stiffness ratio and different mass ratio (The stiffness ratio is 0.1)

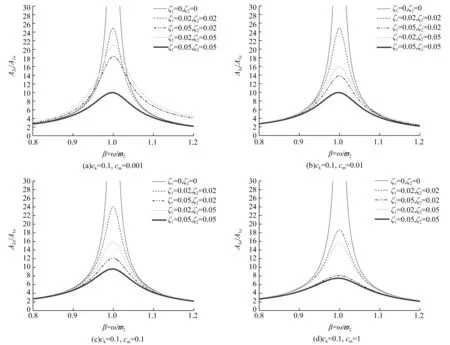
图5 质量比等于刚度比时的幅频特性曲线Fig.5 Amplitude frequency characteristic curve when mass ratio is equal to stiffness ratio

综合分析图3、图4和图5，可总结出以下几点规律：

2)当结构一阶振型阻尼比与结构二阶振型阻尼比相等时(ζ1=ζ2)，随着阻尼比的增大，鞭梢效应得到减弱，在阻尼比较小时随着刚度比ck、质量比cm的增大可以减小振幅比的数值如图5(d)，但从整体上来看对振幅比A2a/A1a的影响不大，规律并不明显。

3)当ck远大于cm(图3(a)、图3(b)，图4(d))时，振型阻尼比组合ζ1=0.02，ζ2=0.05的曲线峰值位于阻尼比组合ζ1=0.05，ζ2=0.02的曲线峰值之下，说明ζ2的影响比ζ1大，随着ζ2的增大鞭梢效应减弱；当ck=cm或ck小于cm(其他各图)时，则刚好相反，ζ2的影响比ζ1小，其中当ck远小于cm(图3(d)，图4(a)、图4(b))时，ζ1=0.02，ζ2分别取0.02，0.05时的曲线几乎重合，ζ1=0.05的两条曲线也几乎重合，说明此时ζ2的影响很小，几乎可以忽略不计，随着ζ1的增大鞭梢效应减弱。

4 结 论

本文针对双自由度体系鞭梢效的影响因素进行了系统的研究得出以下几点结论：

1)对于无阻尼体系，鞭梢效应仅与频率比有关，当外激励频率与上部结构的自振频率相等时，上部结构与下部结构绝对位移振幅的比值达到无穷大，引起强烈的鞭梢效应。

2)对于有阻尼体系，当结构的两阶振型阻尼比相等时，增大阻尼比可减弱鞭梢效应，刚度比和质量比对鞭梢效应影响不明显；若结构的两阶振型阻尼比不相等，当刚度比远大于质量比时，二阶振型阻尼比比一阶振型阻尼比对鞭梢效应的影响大；当刚度比小于质量比或刚度比等于质量比时，一阶振型阻尼比比二阶振型阻尼比对鞭梢效应影响大。