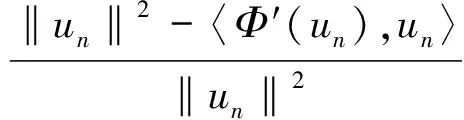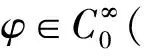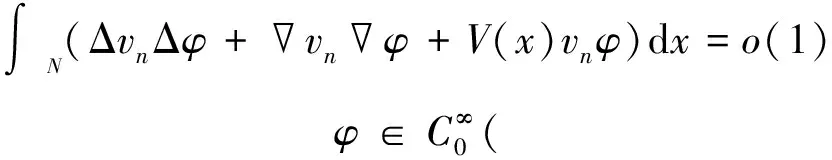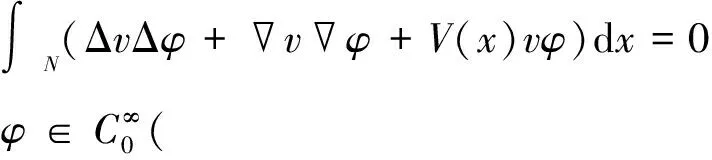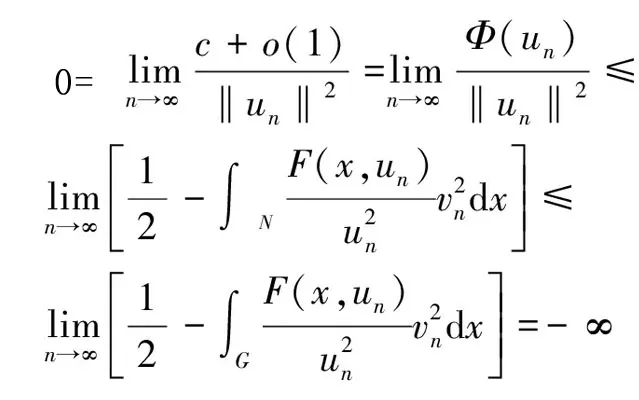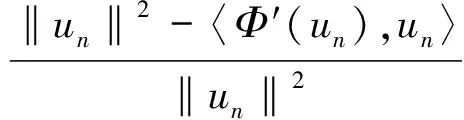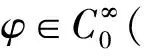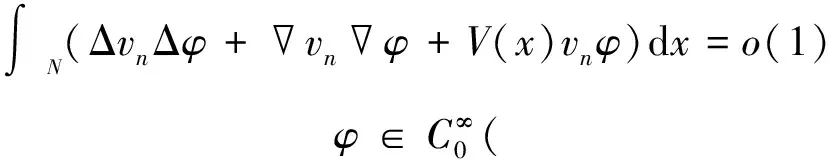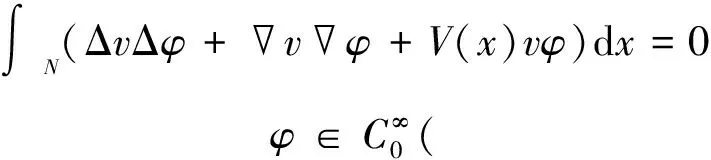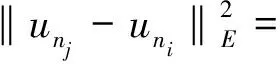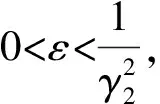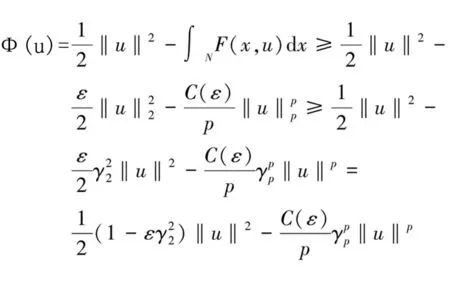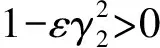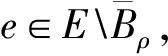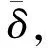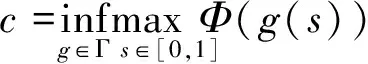一类四阶椭圆型方程解的存在性

阳 晃,陈会文,李家萌

(南华大学 数理学院,湖南 衡阳 421001)

0 引 言

考虑下列四阶椭圆型方程：

(1)

四阶椭圆方程产生于研究悬桥周期振动中的行波问题[1]和研究静态偏转的弹性板问题，大量应用于物理、化学等现象中，因此受到了广泛研究和关注。对于求解高阶椭圆型方程，运用变分法可以巧妙地将寻找方程解的问题化为寻找相应能量泛函临界点的问题。1973年A.Ambrosetti和P.H.Rabinowitz提出的山路引理为在变分框架下研究解的存在性及多重性提供了强有力的工具，随后各类四阶椭圆方程解的存在性和多重性等问题便成为学者们的研究热点之一，其中就有许多学者研究了四阶椭圆方程的解(参考文献[1-11])。确切地来说，Y.L.Yin和X.Wu(参考文献[4])研究了问题(1)，他们利用变分方法得到了下面定理。

定理1 若f满足下列条件：

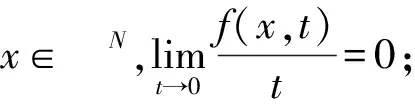
则问题(1)存在一个非平凡解。

定理2 若f满足(V),(f1)和(f2)以及下列条件:

则问题(1)存在一个非平凡解。

注1：(f3)和(f4)暗示了(f5)和(f6)，则定理1推广了定理2。

之后有学者引入参数λ研究了如下方程

例如J.Liu和S.X.Chen等人在文献[9]中假设V，f(x,u)满足类似文献[4]中的假设条件，同样利用变分方法得到了非平凡解的存在及多重性。

随后，Zhang和Tang等人在文献[10]中假设V满足下列假设条件：

(V1′)存在一个常数d0>0，有

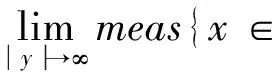
V(x)≤M}=0,∀M>0

本文对一类四阶椭圆方程非平凡解的存在性进行了研究，并对f(x,u)作新的假设条件，故将使用以下条件：

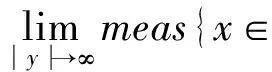
∀M>0

关于a.e.x∈G一致成立；

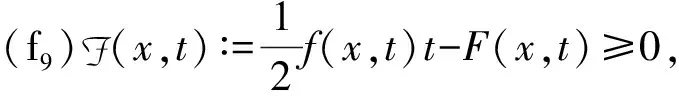
|t|≥R0且N>4

以及对一些κ∈(1,2/(1-σ)]

且N≤4。

定理3 假设满足(V′),(f1)和(f7)～(f9)条件，则问题(1)有一个非平凡解。

注2：很容易看出，(V′),(f8)和(f9)弱于(V),(f3)和(f4)，其中(f8)是局部超线性条件，由此建立了一个新的存在性准则。

例1：当N>4且F(x,t)=[sin(2πx1)+ |sin(2πx1)|]t2ln(1+t2)，

则

1 预备知识

在希尔伯特空间

其中内积表示为

相关范数为

‖u‖s≤γs‖u‖,∀u∈E

(2)

(3)

故有下列引理：

(4)

此外，Ψ′:E→E*是紧性的，E*是E的对偶空间，其中

(1)Φ(0)=0；

(2)存在常数ρ,α>0，使得Φ|∂Bρ≥α；

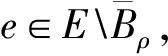
则Φ有一临界值c≥α，且

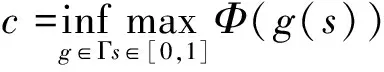
其中

Γ={g∈C([0,1],E):g(0)=0,g(1)=e}。

注记1 文献[16]的结果表明，从(C)条件下可以得到一个形变引理和一个指标理论，这是得到临界点定理的基础。在文献[15]中，可以证明如果采用(C)条件而不是(PS)条件，就可证明引理4仍然成立。故当任意序列{un}满足

I(un)→c,‖I′(un)‖(1+‖un‖)→0

(5)

2 定理3的证明

引理5 满足假设(V′)，如果Aω=-Δ2ω-Δω+V(x)ω，且ω|G=0，则ω=0。

引理6 假设满足(V′)，(f1)和(f7)～(f9)条件，{un}⊂E满足Φ(un)→c，‖Φ′(un)‖(1+‖un‖)→0，n→∞，则{un}在E中有界。

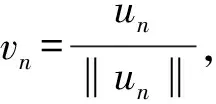
(6)

对0≤a

(1)考虑N>4的情况。

(7)

由Hölder’s不等式，(f9)和式(6)，存在正常数C2，可得

o(1)

(8)

结合式(7)和式(8)，可得

o(1)

故矛盾。

得到

(9)

又因为

(10)

其中C3,C4和C5为正常数。结合式(9)和式(10)得

(11)

因为vn⇀v(n→∞)，由式(11)可知

(12)

这表明Av=-Δ2v-Δv+V(x)v=0。根据引理5，可知v|G≠0，由(f7),(f8)和Fatou’s引理得

故矛盾。

(2)考虑N≤4的情况。

(13)

根据Hölder’s不等式，(f9)和式(6)，对一些κ∈(1,2/(1-σ)]，取κ′=κ(σ+1)/(κ-1)，存在正常数C7，有

(14)

结合式(13)和式(14)，可得

(1)

故矛盾。

得到

(15)

又因为

(16)

其中C8,C9和C10为正常数。结合式(15)和式(16)得

(17)

因为vn⇀v(n→∞)，由式(17)可知

(18)

这表明Av=-Δ2v-Δv+V(x)v=0。根据引理5，可知v|G≠0，由(f7),(f8)和Fatou’s引理得

故矛盾。综上所述，所以{un}在E中有界。

引理7 如果un⊂E满足Φ′(un)→0，且是有界序列，则un⊂E有收敛子序列。

证明：由引理2可知，{un}有一个{unj}子序列，且取点u∈E，使得‖Ψ′(unj)-Ψ′(u)‖E*→0，其中nj→∞，因此

〈Ψ′(unj)-Ψ′(uni),unj-uni〉≤

(‖Φ′(unj)‖E*+‖Φ′(ui)‖E*)×

‖unj-uni‖E+‖Ψ′(unj)-

Ψ′(uni)‖E*‖unj-uni‖E→0,

(i→∞,j→∞)

这就说明了{unj}是E中的柯西序列，由于E的完备性，可知{unj}在E中有收敛序列。

引理8 在满足假设(V′),(f1)和(f7)下，存在常数ρ,α>0，使得Φ|∂Bρ≥α。

|f(x,t)|≤ε|t|+C(ε)|t|p-1,

且

(19)

由(V′),式(2),式(3)和式(19)可知，得

证明：由(f8)可知，对任意的k1>0，存在T1>0，使得

F(x,u)≥k1|u|2,∀x∈G,|u|≥T1

(20)

对任意ζ>0，存在一个闭集G1和一个开集G2，使得G1⊂G⊂G2，且

meas(G1)>0,meas(G2G1)<ζ,

meas(GG1)<ζ

(21)

选取k1足够大的时候，则

定理3的证明：由引理6～引理9可知，Φ满足引理4的所有条件，则Φ有一临界值c≥α，且

其中Γ={g∈C([0,1],E):g(0)=0,g(1)=e}

因此，存在u*∈E，使得

Φ(u*)=c且Φ′(u*)=0

则u*是问题(1)的解。