课程思政融入线性代数课程教学的实践

张四保

（喀什大学 数学与统计学院，新疆 喀什 844006）

线性代数作为代数学的一个分支，是高等学校非数学专业理工科、经管类等各专业一门必修的专业基础理论课.它主要研究有限维线性空间与线性变换等相关的基本理论，以矩阵为基础，以行列式和矩阵的运算为工具，以向量组的线性相关性和线性方程组的理论为核心，着重解决了方阵可对角化和化二次型为标准型的理论与方法问题.通过本课程的开设，使学生掌握线性代数的基本概念、基本理论与基本方法，以培养学生的抽象思维能力、逻辑推理与判断能力、空间想象能力和数学语言及符号的表达能力，提高学生综合运用所学的基本概念、基本理论、基本方法分析问题和解决问题的能力，并逐步培养学生科学创新、严谨求实的作风.

课程思政，即将思想政治教育元素，包括思想政治教育的理论知识、价值理念以及精神追求等融入到各门课程中去，潜移默化地对学生的思想意识、行为举止产生影响[1].

2020 年5 月教育部发布的《高等学校课程思政建设指导纲要》明确指出，要把思想政治教育贯穿人才培养体系，全面推进高校课程思政建设，发挥好每门课程的育人作用，提高高校人才培养质量.在2021年2 月初教育部高等教育司印发的《教育部高等教育司2021 年工作要点》中，将全面加强高校课程思政建设列为2021 年工作要点，并明确要求要紧紧抓住教师队伍“主力军”、课程建设“主战场”、课堂教学“主渠道”，健全完善所有高校、所有教师、所有课程育人网络，使各类课程与思政课程同向同行，构建全员、全程、全方位育人大格局.如何高效地把思政元素贯穿于各个学科的课堂教学中，是一项创新与开创性的工作，也是在高校课堂中实施课程思政的困难所在[2].

全面推行课程思政建设是新时代高校思想政治工作的重要举措[3].在课程思政教育理念下，如何在课程教学中融入课程思政教育是一个值得教育工作者必须思考并在实践教学中严格落实的问题.本文就如何发掘线性代数课程的思政元素提出一些想法，以期对相关教育工作者有所启发与帮助.

1 基于特定的数字意义发掘思政元素

在课程课堂教育教学过程中，教师可以从一些特定的数字出发，巧妙地引入“民族团结”、“校史、校风”等思政元素，帮助青年大学生树立全国各民族大团结、爱校护校等思想意识[4].

校史是高等院校校园文化建设的一项十分重要的内容，具有重要的育人作用.从学校发展进程中一些具有特定历史意义的时间年份数字出发，深入挖掘课程思政内容.以喀什大学为例，在学习分块矩阵时，任课教师可构建类似的矩阵，在给学生讲解矩阵分块的同时，利用数字进行课程思政教育.按照行分块，矩阵A可分成6 个子块，每个子块都可构成一个四位数的数字，从而由这6 个数字引入校史、民族团结、校风等思政元素.

喀什大学办学始于1962 年，校名为喀什师范专科学校，是当时新疆维吾尔自治区5 所高等院校中唯一的高等师范院校，在新疆特别是南疆社会稳定、基础教育和经济社会发展等方面发挥了十分重要的作用.学校在1978 年升为本科院校，更名为喀什师范学院.在1994 年和2009 年两次被国务院授予“全国民族团结进步模范集体”光荣称号.学校在2015 年更名为喀什大学，2016 年被列为全国100 所转型发展试点高校之一.充分发挥课堂教学的引领作用，通过这些有关学校发展各阶段重要事件等思政元素的引入，培养学生作为喀什大学学子的自豪感与荣誉感，同时强化青年大学生民族团结意识，在日常的学习、生活中时刻践行民族团结，自觉地转化为他们的情感认同和行为习惯.

2 基于HPM 视角发掘思政元素

数学史对增强数学文化的渗透，弘扬优秀传统文化，感悟数学的价值，提升学生的科学精神、应用意识和人文素养等都有着十分重要的现实意义和深远的历史意义[5].HPM 是研究数学史与数学教育关系的国际教育组织[6]，它始于1972 年召开的第二届国际数学教育大会上成立的International Study Group on the Relations between History and Pedagogy of Mathematics，简称之为HPM.HPM 其功能在于通过数学史寻找数学教育的规律和经验，把数学知识的历史形态加工整理成教师和学生能够方便使用的教育形态，使数学史为生动活泼的数学教学服务.数学史是人类在数学研究与探索道路上奋进的历史，不仅包含着许多令人鼓舞、令人奋进、引人自豪的史料，也包含着许多重要的数学思想及方法[7].

2.1 基于知识点的相关史料发掘思政元素

在讲解线性方程组时，向学生介绍我国在方程组方面的巨大成就，如2020 年4 月被列入《教育部基础教育课程教材发展中心中小学生阅读指导目录（2020 年版）》初中段的《九章算术》《孙子算经》《数书九章》《方程论》（清代数学家梅文鼎著）等所涉及到方程组的内容，使学生感受我国劳动人民的伟大成就与智慧，以增强其民族自豪感与自信心，坚定文化自信，正如清代数学家梅文鼎向堪称数学大全的《数度衍》的作者方中通所说“方子精西学，愚病西儒排西算，著《方程论》，谓虽利氏无以难”，其大概意思是：我国古代在线性方程组的研究成果是西方数学界难以比拟的，我们完全没有必要在欧美学者面前妄自菲薄.

在线性方程组的研究方面，我国较欧洲至少早了1 500 多年.在大约成书于公元一世纪的我国古代数学巨著《九章算术》第八章方程组中，记载这样的问题：“今有上禾三秉，中禾二秉，下禾一秉，实三十九斗；上禾二秉，中禾三秉，下禾一秉，实三十四斗；上禾一秉，中禾二秉，下禾三秉，实二十六斗.问上、中、下禾实一秉各几何”[8-9]，对这一问题，在《九章算术》中给出了算筹图.

对于该问题，如果用现在的数学语言来表示就是三元一次线性方程组，式中：x，y，z分别表示上禾、中禾、下禾各一秉的实的数量；而所给出的算筹图就是现行教材中的增广矩阵.在《九章算术》采用分离系数的方法来表示线性方程组，这就相当于现行教材中的矩阵；解线性方程组所采用的是直除法，这与现行教材中的矩阵初等变换的原理一致.这是世界上对一次线性方程组的解法最早、最完整的刻画，而在西方，直到17 世纪德国数学家莱布尼兹才提出完整的求解线性方程组的法则.作为一部世界数学名著，《九章算术》早在隋唐时期即已传入朝鲜、日本，它已被译成日、俄、德、法等多种文字版本.

2.2 基于数学家的研究成果及历程发掘思政元素

在数学漫长的发展演变进程中，数学家所创造积累的光辉成就以及他们孜孜不倦地追求真理所表现的种种感人事迹和精神品质[10]，不仅展示了数学家开拓创新、追求真理的科学精神，也展现了数学家忠诚爱国、献身事业的高尚情怀[11]，这为大学生的精神文化塑造提供了良好的思政素材.

线性代数是一门高度抽象的数学课程.在学习的过程中，对某些具有一定计算量且繁琐的内容，如高阶行列式的计算、行数与列数较高时矩阵的乘法、多个未知数多个方程的线性方程组的求解、利用正交变换化二次型为标准形（或规范形）以及求一正交矩阵P，使P-1AP=Λ（A是一实对称方阵）为对角阵等，学生往往会产生畏难情绪，在一定程度上对课程学习失去兴趣与信心.在教学过程适时地引入我国老一辈数学家的轶事，使学生学习我国老一辈在逆境中潜心学习、忘我钻研的精神，提高学习数学的兴趣，以帮助学生逐步端正学习态度.

1742 年，德国数学家哥德巴赫提出数学界的著名猜想：任一大于2 的偶数都可写成2个素数之和，简称1+1.我国数学家陈景润院士在高中阶段，遇到了令他终生难忘的沈元老师.沈元见陈景润能够快速地解答“韩信点兵”问题，就鼓励他去摘取皇冠上的明珠——哥德巴赫猜想.为此陈景润立誓：长大无论成败如何，都要不惜一切地去努力.为了使自己梦想成真，陈景润不管是酷暑还是严冬，在那不足6 m2的斗室里，废寝忘食，潜心钻研，光是计算、推理用的演算纸就足足装了几麻袋.终于在1973 年《中国科学》期刊上发表了“1+2”详细证明，引起世界巨大轰动，这一结果被公认是对哥德巴赫猜想研究的重大贡献，是筛法理论的光辉顶点，国际数学界将这一重要成果称为“陈氏定理”，至今仍在哥德巴赫猜想研究中保持世界领先水平.陈景润的事迹在1978 年以后被广为传颂，对尊重知识、尊重人才风气的形成起到了重要作用，也让一大批青年学子深受鼓舞，坚定了科学报国的决心.2018 年12 月18 日，在庆祝改革开放40 周年大会上，陈景润被党中央、国务院授予改革先锋称号，颁授改革先锋奖章，并获评为激励青年勇攀科学高峰的典范[12].

3 基于自然科学方法论发掘思政元素

自然科学方法论是培养学生科学素质的有效指导理论.在教育教学过程中，自然科学方法论在指导学生学习科学知识以及培养学生科学精神等方面都有着积极的指导作用.在课堂教学过程中，教师应紧密结合课程知识点，运用科学方法论深入挖掘课程内容的思政元素，积极培养学生的科学素养.

案例n阶行列式的定义.

先介绍二阶行列式和三阶行列式的构造.

二阶行列式的构造为

由式（1）可以看出，二阶行列式的结构特点为：（1）二阶行列式为2=2!项的代数和，每一项都是2个位于不同行不同列的元素的乘积，若把每一项2 个元素的行标按自然排列，除不考虑符号外每一项都可以写成a1p1a2p2的形式，其中列标排列p1p2是1 与2 这2个数的一个排列，这样的排列共2 项.（2）由于每一项的行标排列都是自然排列，每一项所带的符号与行标排列无关，现只需考虑列标排列.项a11a22列标排列12 的逆序数为0，是一个偶排列，项a11a22带“+”号；项a12a21列标排列21 的逆序数为1，是一个奇排列，项a12a21带“-”号.

三阶行列式的的构造为

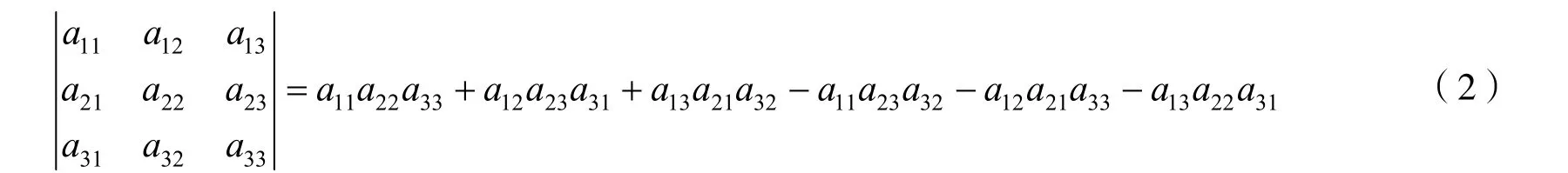
由式（2）可以看出，三阶行列式的结构特点为：（1）三阶行列式为6=3!项的代数和，每一项都是3个位于不同行不同列的元素的乘积，若把每一项3 个元素的行标按自然排列，除不考虑符号外每一项都可以写成a1p1a2p2a3p3的形式，其中列标排列p1p2p3是1，2，3 这3个数的一个排列，这样的排列共6=3!项.（2）由于每一项的行列排列都是自然排列，每一项所带的符号与行标排列无关，现只需考虑列标排列.项a11a22a33，a12a23a31，a13a21a32的列标排列分别为123，231，312，它们的逆序数分别是0，2，2，都是偶排列，则项a11a22a33，a12a23a31，a13a21a32带“+”号；项a11a23a32，a12a21a33，a13a22a31的列标排列分别为132，213，321，它们的逆序数分别是1，1，3，都是奇排列，则项a11a23a32，a12a21a33，a13a22a31带“-”号.

通过对二阶行列式、三阶行列式构造的分析，总结类推给出n阶行列式的定义.

n阶行列式等于所有位于不同行不同列的n个元素乘积的代数和，每一项都可以写成(-1 )τa1p1a2p2…anpn的形式，即

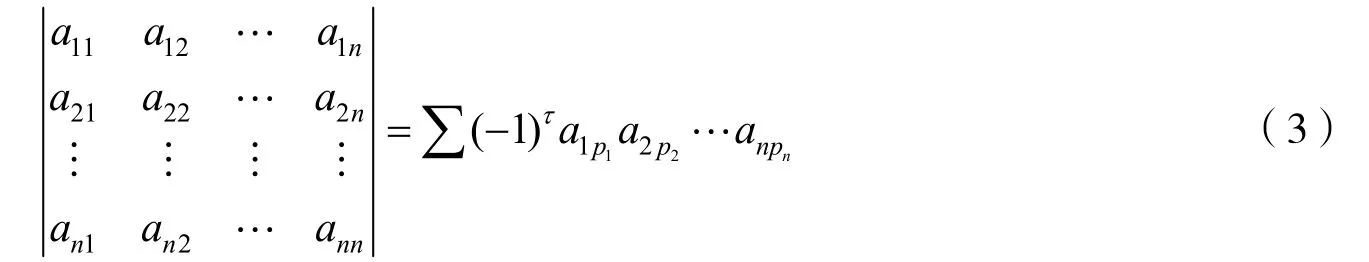
式中：列标排列p1p2…pn是1，2，…,n这n个数的一个排列，共有n!项；τ是列标排列p1p2…pn的逆序数.

对于以上的教学内容，在教学的过程中，教师可以提出2个问题让学生思考，以提高学生分析问题与解决问题的能力，培养其科学探索精神.

问题1在n阶行列式的定义（3）中，在考虑每一项所带的符号是“+”还是“-”时，是将每一项元素的行标按自然排列来进行考虑的.如果将每一项元素的列标按自然排列，那么项所带的符号该如何确定.试对二阶行列式和三阶行列式进行考虑，类推给出每一项元素的列标按自然排列时n阶行列式的定义或者表达式.

问题2在n阶行列式的定义（3）中，在考虑每一项所带的符号是“+”还是“-”时，是将每一项的元素行标按自然排列来考虑，同样也可以根据问题1 先将每一项的元素列标按自然排列来考虑.如果每一项元素的行标排列与列标排列都不是自然排列，那么项所带的符号该如何确定.试对二阶行列式和三阶行列式进行考虑，类推给出每一项元素的行标排列与列标排列都不是自然排列时n阶行列式的定义或者表达式.

通过案例的教学安排，用自然科学方法论有意识地培养学生充分利用循序渐进的方式与方法认识问题、分析问题的能力，帮助学生牢固树立起从点滴做起，积跬步以致千里的理念[13]，用科学严谨的方法分析问题和解决问题，提升自身的科学素养.

4 结语

线性代数课程的开设班级为理学、工学、管理、经济学等学科一年级本科生[14].而刚入校的学生相对来说年龄较小、思想活跃，易于接受与理解新思想，因而在线性代数课堂上讲好课程思政具有很重要的意义，对学生的世界观、人生观、价值观等的培养具有重要作用.本文针对线性代数课程中融入课程思政问题，从特定的数字意义、HPM 视角、自然科学方法论这3 个方面，阐述发掘课程思政元素相关做法.教学实践表明，这些措施有助于将传授知识技能与培育理想信念相结合，构建全课程育人格局，达到了立德树人的育人目标.