数学分析中开展课程思政教学的实践——以高阶导数的教学为例

邓宇龙，张建国

（长沙师范学院 数学科学学院，湖南 长沙 410100）

现代数学是以微积分理论为基础的分析数学，而数学分析研究的主要内容是微积分.数学分析课时长、教学内容多，是数学专业解决“为谁培养人”问题的第一基础课程，是很多后续专业课程的先导课程.因此，高校数学教师要用好数学分析课堂教学这个主渠道，把立德树人作为教育的根本任务，真正做到课程与思政同向同行.这必然要求在数学分析的课程建设中突出课程思政理念.

高阶导数是微分理论的重要组成部分，在函数的极值、凹凸性和拐点以及Taylor 公式等问题的研究中有举足轻重的作用.因此，高阶导数在数学分析中意义重大.高阶导数中蕴含有丰富的课程思政元素，高校教师可以在高阶导数的概念教学中培养学生的数学发散思维、演绎逻辑推理思维、归纳概括思维、应用思维和转化思维等基本数学思维；在高阶导数的计算和几个常用的高阶导数公式教学中引领学生健康的世界观和人生价值观；在高阶导数的Leibniz 公式教学中融入数学文化以及蕴藏的人文素养，激发学生学习数学的兴趣.本文以高阶导数的教学实践为例，论述高校教师如何在数学分析课程教学中开展课程思政.

1 在高阶导数的概念教学中培养数学思维

数学的重要性不仅在于它具有强大的工具性，还在于它具有强大的育人功能.数学知识承载着数学思维，是极好的思维训练手段，它的育人功能首先体现在人的思维能力培养方面[1].数学思维至少有2种：一种是逻辑思维，它保证了数学的严密性；另一种是应用思维，它把数学理论应用到实际生活中.人们通过数学思维的培养和训练，在遇到问题时，能够抽象概括并提炼出问题的实质，多方位开辟思维点，再根据条件的变化改变问题的思考方向，创新性地解决问题.

培养数学思维能力的过程是一个循序渐进的过程，在高阶导数概念的教学中可以逐步培养学生的数学发散思维、演绎逻辑推理思维、归纳概括思维、应用思维和转化思维等基本数学思维能力.按照数学分析课程内容的编排，学生在学习高阶导数时，已经完成了导数的概念和计算的学习以及对导数几何意义的理解[2].因此，在高阶导数课前10 min，可以利用学习通、云课堂等在线学习平台，精选发布5 个左右的选择、填空或者判断题，要求学生在规定的时间内完成.考虑到接下来的教学内容，课前练习的组题既要承接旧知，又要启发新知.例如：求某些函数的导数；求已知曲线的切线方程或斜率；利用导数的定义求一些未知的参数；导数定义的变形；求一些简单函数的高阶导数等.

这些组题既复习了导数的计算性质和几何意义，又回顾了导数的概念

和导数定义公式的变形，加深了函数在点x0的导数是一个数的认识，且学生应用所学知识解决实际问题的能力得到了较好的锻炼.由于选择、判断、填空题完成的时间较短，教师可以利用学习通、云课堂等在线学习平台即时反馈学生习题完成情况，还可以让完成速度快且质量好的学生分享解题的经验和心得.课前练习的反馈激发了学生学习数学分析课程的兴趣，训练了思维的敏捷性，体会到数学对实际问题解决的作用.这种寓教于乐的作业形式得到了学生的喜爱，学生在课前练习中得到了充分的展示机会，相互之间形成了良性的竞争，学风焕然一新.

为了启发学生对高阶导数概念的探索，可引导学生思考：如果一阶导函数f′(x) 还可以继续求导数，应如何给出这个定义.学生通过导数概念的复习，运用发散思维后可以很快地给出回答：若函数f(x) 的导函数f′(x) 在点x0可导，则有导函数的导数

依此类推，可以引导学生给出二阶导数的定义，并层层演绎出三阶导数等概念，归纳总结出高阶导数概念.

由此可见，高阶导数的定义是一个循序渐进的过程，通过对这个概念的层层解读，不仅培养了学生的数学发散思维、演绎逻辑推理思维、类比思维和归纳概括思维等基本的思维能力，同时，也让学生体会到了数学定义的严密、细致和逻辑推理的严谨性.

2 在高阶导数的计算过程中引领人生情感

“师者，传道、授业、解惑也”，这句话生动地概括了教师的2大职责——教书和育人.教师，在传授学生知识的同时，还要兼顾教导学生做人的道理.高阶导数概念晦涩难懂，给人“高大上”的错觉，但在高阶导数的计算和表达公式中也蕴含了一些人生哲理和为人处世之道.通过对高阶导数的计算和表达公式中隐含的人生哲理和为人处世之道的解读，不仅能活跃课堂气氛，提高学生学习兴趣，还能帮助学生明白做人做事的基本道理，实现教师教书和育人的宗旨.

根据高阶导数的定义可知，要求得函数的高阶导数，就需要对比它低一阶的导函数再求一次导数.因此，利用高阶导数概念来求解函数的高阶导数是最基本的方法.

例1求幂函数f(x)=xn（n为正整数）的各阶导数.

解由幂函数的求导公式可知，f′(x)=nxn-1，f′ (x)=n(n-1)xn-2，…，f(n)(x)=n!，f(n+1)(x)=0，….

显然，利用高阶导数的定义求函数的高阶导数是一个循序渐进、连续求函数一阶导数的过程.因此只需要利用一阶导数的求导法则，对函数逐阶求导即可.换句话说，要求函数的高阶导数，只能先求一阶导数，再求二阶导数、三阶导数等，依次类推，逐步地往上求解，才能得到函数的高阶导数，达到最终目标.这正如我们的学习、生活以及工作，无论做什么事情，都需要按部就班、脚踏实地地去做，没有捷径可寻，“三天打鱼，两天晒网”行不通，一蹴而就更不可能.

例2求函数f(x)=sin（x）的各阶导数.

这是基本初等函数求任意阶导数的问题.为找出其中的规律性，可以先具体求出若干阶导数.对于函数f(x)=sin（x），由三角函数的求导公式可知

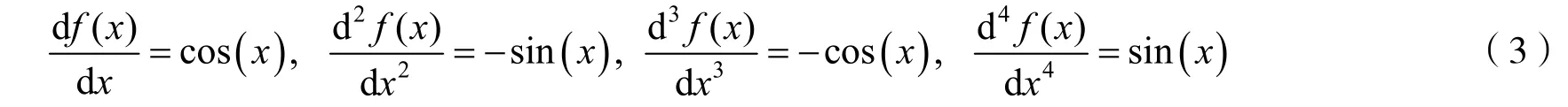
不难发现，sin（x）的高阶导数具有一种循环性，一方面涉及 sin（x）和cos（x）之间的互相转化，另一方面涉及符号交互转化.

还应注意到，当求解一个问题比较繁琐时，可以考虑转换一种思维方式.事实上，在求函数f(x)=sin（x）的各阶导数时，由(u+v)(n)=u(n)+v(n)，(Cu)(n)=Cu(n)可知

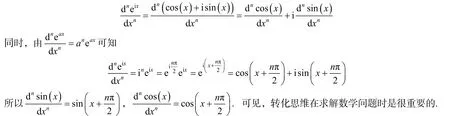
在教学中，经常用xn,ex,sin（x）,ln(1+x)作为求函数高阶导数的实例进行讲解分析.对于正整数幂函数xn，每一次求导，都能把幂次降低1.显然，第n次求导可得一个常数，而求导次数大于n时的导数都等于0；指数函数ex的各阶导数仍是ex；三角函数（x）sin 的高阶导数循环出现；对数函数的高阶导数却发生了改变.这正如人生的4 种态度，即消逝不见、始终不变、周期循环、改变目标.如果把每一次求导当成一次挫折，那么，到底是被挫折磨灭了意志，还是始终坚持初心，或者原地踏步徘徊不前，或者改变最初的理想，在经历几次磨砺后就面目全非亦或荡然无存.我们不禁会问，有没有像函数ex那样，虽历经磨难，但始终不忘初心、坚定信念、百折不挠、勇敢面对的一种誓言[3].

3 在求高阶导数的Leibniz 公式中渗透数学文化

在人们认识世界和改造世界的过程中，数学发挥了关键的作用.它不仅具有深邃的科学精神，还蕴藏着丰富的人文精神.纵观我国古今在数学上取得的丰硕成就，强烈的民族自豪感油然而生.在人类文明的发展进程中，数学是坚实的基础和重要的支柱.人们只有接受数学文化的熏陶和洗礼，才能真正地走近数学、了解数学、领悟数学和热爱数学.教师在教学过程中，应该挖掘数学分析课程蕴含的数学人文精神，帮助学生了解人类文明发展中数学分析知识所起的重要作用，形成正确的数学观.

高阶导数的Leibniz 公式不仅留下了数学家Leibniz 和Lagrange 奋斗拼搏的轶事，还蕴藏着丰富的数学思想方法.

Leibniz 公式用于求2个函数的乘积的高阶导数[4].由乘积求导法则可知

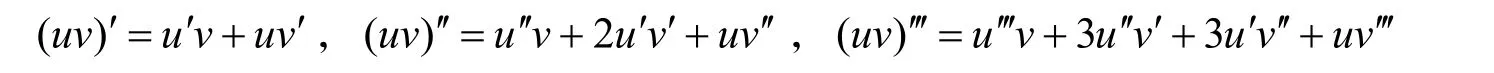
观察(uv)′,(uv)′ ′,(uv)′′′展开式中各项的系数公式，容易发现这是二项式系数.于是，人们通过类比，归纳总结出了Leibniz 公式.

Leibniz 公式若函数u,v有任意阶导数，则

Leibniz 公式在形式上与我国古代数学的杰出成果之一，即二项式(u+v)n展开式系数的杨辉三角相似.杨辉三角把二项式系数的表示图形化，直观地体现出了组合数内在的一些代数性质[5].通过这样的比较关联，既能让学生体会到数学的统一，又能激发学生的文化自信.

此外，教师在教学中还可以穿插数学家Leibniz 和Lagrange 的故事.Leibniz 在数学史和哲学史上都占有重要的地位，他所创立的微积分数学符号被广泛地使用，他的数学成果很多都是在往返于各大城镇的颠簸的马车上完成的.我们有整洁的教室和教学楼，窗明几净，因此更应该珍惜现在求学的好时光.

18 岁的Lagrange 曾独立地推出了Leibniz 公式，他兴奋地把论文寄给大数学家Euler.然而，Euler 却告之Leibniz 在半世纪前就已经得到了这个结果，这个“不幸”的消息非但没有使Lagrange 泄气，反而激发了他钻研数学的信心，给出了著名的Lagrange 中值定理.因此，在面对挫折时，更应该坚定信念，把挫折化作前进的动力.

总之，数学分析中的定理、公式，甚至于一个表达符号的背后都蕴含了动人的故事，包藏了满满的人文精神.教师在教学中融会贯通，挖掘隐藏在Leibniz 公式中的数学思维方法和数学家的故事，不仅能巩固学生对高阶导数知识点的掌握，还活跃了课堂气氛，提升学生学习高阶导数的兴趣.学生在不自觉中接受数学文化的熏陶，不但学习到数学家的奋斗精神，更容易理解和领悟Leibniz 公式在求解高阶导数中的作用.

4 在数学分析课程教学实践中融入课程思政元素的关键

从课程思政融入到高阶导数的教学实践来看，把课程思政渗透到数学分析的教学中，不仅有利于克服传统教学中概念、定理、计算公式罗列堆积的不足，还有利于培养学生应用数学思想分析问题、解决问题的能力，提升数学学习的趣味性，增强数学课堂引领作用.在数学分析课程的教学实践中融入课程思政元素，以数学知识吸引学习兴趣，以数学素养影响良好人格，以数学文化浸润美好心灵.

4.1 注重培养学生的数学精神和数学思维能力

高校数学教师要注重培养学生的数学精神和数学思想方法.数学思维能力是人脑按一定思维规律认识数学对象的数学内容的内在理性活动，是人们运用数学观点思考问题、解决问题的能力.它包括抽象概括能力、推理论证能力、空间想象能力、运算求解能力、数据处理能力、应用意识和创新意识等7个方面.

培养数学思维能力是数学教育的根本目的，也是最重要的课程思政.因此，数学教学改革的一个重要课题在于如何锤炼学生的数学思维能力，形成良好的数学品质.培养数学思维要遵循数学学科的特点，如果只讲知识，不讲精神；只讲技巧，不讲思想，学生就不能掌握数学的精髓，真正地领悟数学[6].数学基本概念、定理是进行数学论证的理论基础，因此，高校教师既要注重基本概念和定理的教学，又要理解蕴含其中的数学精神；既要注重数学的基本运算和应用技能的教学，又要引导学生思考蕴含其中的数学思维方法.

4.2 教师既要当“经师”又要当“人师”

高校数学教师既要当“经师”，又要当“人师”.为师之道，自古就有“经师”和“人师”之说.经师把教师职业当作谋生的手段，他们认真钻研业务，扎实掌握基本技能，严肃、严谨、严格对待教育和教学工作，对教育事业有着积极的推动.

然而，经师只是作为教师的起码要求，人师才堪称人类灵魂的工程师.人师把教师职业当作事业的追求和精神的享受，他们有高深的学问以及伟大的人格和高尚的修养，陶冶着学生的人格.中国教育的传统观念，要求教师除了有经师之范外，还要有人师的境界，以自身的人格魅力、德才情操潜移默化地感化和塑造学生人格.著名的无产阶级教育家徐特立老先生就提出过“经人合一”的教育思想.“经师”和“人师”正是教师职业传播知识和真理以及塑造灵魂和人格的职业定位，二者的统一就是专业知识和课程思政的有机融合.

4.3 注重用数学文化浸润学生的心灵

高校数学教师要注重用数学文化浸润学生的心灵.狭义的数学文化指数学思想、精神、方法、观点、语言以及它们的形成和发展；广义的数学文化在狭义的数学文化内涵基础上，还兼顾了数学家、数学史、数学教育、数学与人文的交叉、数学与各种文化的关系等[7].数学文化作为数学知识的载体，是连接感性认识和理性认识的桥梁，有深厚的数学教育内涵.数学文化由数学精神、数学思想和数学史组成.数学精神主要有数学理性精神、数学求真精神、数学创新精神、数学合作与独立思考精神等[8].数学中大胆的猜测、奇特的构思以及缜密的推理构成了数学思想的特质[9].数学精神和数学思维体现了对真理的探索精神.数学史蕴含了数学的思想、方法、精神及其发生和演进过程，揭示了数学家的文化活动以及数学在人类文明进步中的巨大作用[10].数学史揭示了数学知识的起源、产生和发展过程.可见，如果不了解承载了数学知识的数学文化，分裂地看待数学与现实世界，学生就会缺乏学习数学的积极性.在数学教学中融入数学文化，开展有效的课程思政，能最大限度地提升学生学习的主动性和积极性.

5 结语

值得注意的是，数学分析课程主要讲授的还是数学的经典知识，即以极限概念为基础的微积分知识.高阶导数作为数学分析课程的一个细微而重要的部分，课程思政元素在其中的渗透应该是相向而行、润物无声，而不能喧宾夺主，淡化了学生对高阶导数概念的理解和掌握，冲淡了学生对数学经典知识的学习.