运用磁悬浮小球改进PID 控制特性教学方法
陈琳琳,任元,王丽芬,刘政良
(航天工程大学 宇航科学与技术系,北京 101416)
PID 控制特性是学生学习自动控制原理课程必须掌握的一个基本控制规律,也是控制类专业学生必须掌握的知识.传统PID 控制特性的教学方法通过概念讲解加上理论推导为主[1-4],学生对PID 控制特性的理解较为肤浅,不能和实际工程应用结合起来,无法彻底掌握PID 控制特性在控制系统中的作用.
在磁悬浮小球控制系统“稳”“快”“准”控制的需求牵引下,本文首先建立磁悬浮小球的重力控制系统数学模型;然后,基于时域分析和频域分析等手段,分析PID 控制器的参数变化对磁悬浮小球重力控制系统性能的影响,实现对磁悬浮小球的重力控制.该教学模式能够引导学生以工程需求为牵引,引导学生伴问题而思考,化抽象为具体,调动学生对学习理论知识的兴趣,提升学生从物理问题-数学问题-科学问题-工程实践的分析问题和解决问题的能力.
1 磁悬浮小球控制原理
磁悬浮小球处于线圈绕组产生的磁场中,磁悬浮小球控制系统主要由铁芯、线圈、位置传感器、放大器、数字控制器和控制对象小球组成[5].当电磁铁上的线圈绕组通电时,小球靠近某个线圈时,会受到线圈产生磁力的吸引力;同时磁悬浮小球也会受到重力的影响,通过设计PID 控制器,将磁悬浮小球稳定在中心位置,且不出现振荡.
在磁悬浮小球系统中,调节电流,使小球的位置z始终保持在平衡位置.忽略小球受到的其它干扰力,小球在系统中只受电磁吸力和自身重力.小球在竖直方向的动力学方程描述为

式中:m为磁悬浮小球的质量,单位:kg;g为重力加速度,单位:m/s2;z为磁极到小球的气隙,单位:m;i为电磁铁绕组中的瞬时电流,单位:A;F(i,z)为电磁吸力,单位:N.经过拉普拉斯变换,根据式(1)推导出电磁铁线圈的传递函数G0(s)为


如果式(2)中的ki=1,m=1,kh=0.02,则电磁铁线圈的数学模型简化为

式中:Ks为气隙与电压的关系系数,单位:V/mm;Ka为功率放大器的增益.
2 P 控制
比例控制器的传递函数为[8-9]

式中:KP为比例系数;e(t)为误差信号(输入信号);uP(t)为输出信号.根据式(1)~(4),推导出磁悬浮小球重力方向控制系统的闭环传递函数Φ(s)为

根据式(6),从磁悬浮小球重力方向控制系统闭环特征根得出结论:当KP>0.02时磁悬浮小球处于临界稳定状态;KP<0.02时磁悬浮小球位置是发散的,即磁悬浮小球处于不稳定状态.式(6)可以进一步化简为

式中:ωn为振荡频率.根据式(7),当系统的输入为单位阶跃函数时,二阶系统的单位阶跃响应(c t) 为

当式(8)中KP分别取50 和0.1 时,系统稳态响应(c t)分别为

根据式(9)~(10),系统稳态响应的Matlab[10]仿真曲线见图1,当KP=0.1时,磁悬浮小球位置处于稳定状态,随着KP增大,磁悬浮小球振荡频率增大,但其振荡幅值减小;当KP=50时,磁悬浮小球处于振荡状态,同时系统超调也增加.
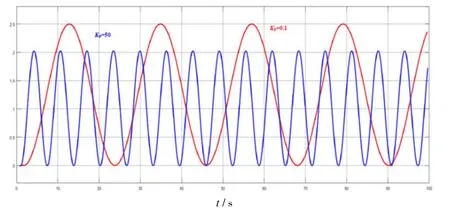
图1 KP 分别取50 和0.1 时系统单位阶跃响应曲线
3 PD 控制
为了解决P 控制下的磁悬浮小球系统的超调和振荡,需要加入微分控制.PD 控制的微分方程为[8-9]

式中:KD为微分系数;uPD(t)为输出信号.在磁悬浮小球控制系统的比例控制基础上增加微分控制,保持比例系数KP=0.3不变的情况,微分系数分别取KD=8,KD=50,系统稳态响应的仿真曲线见图2.
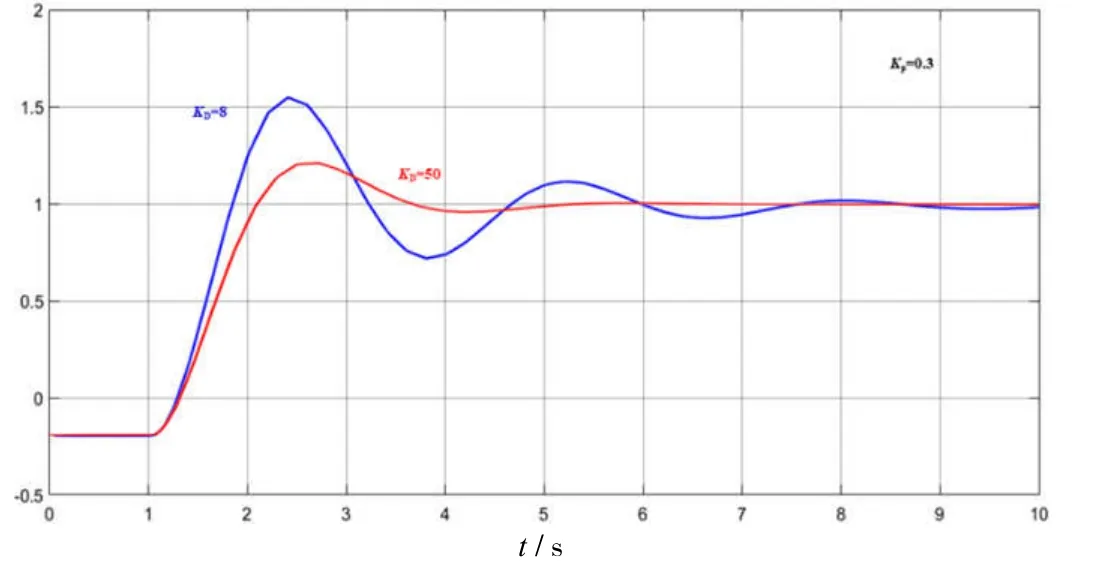
图2 KD 参数不同时系统单位阶跃响应曲线
从图2 中可以看出,微分参数增大,微分作用越强,输出响应的超调减小,调节时间缩短,但是上升时间和峰值时间增加,即系统的动态响应速度变慢.如果从频域方面分析,系统的截止频率增加和稳态裕度均增加,而稳定裕度增加,超调量、调节时间减小,与时域分析结果一致.
磁悬浮小球的位置稳态误差为
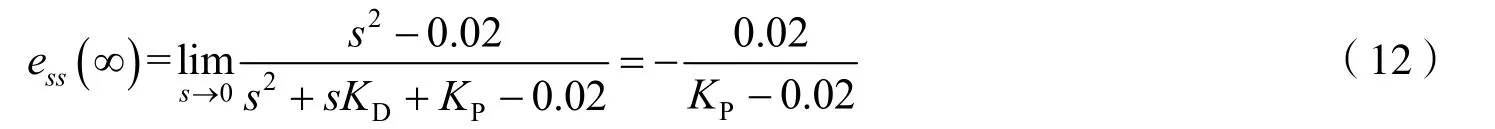
在PD 控制下,系统误差与比例控制器的系数有关,且系统稳态误差无法消除.
4 PID 控制
为了解决PD 控制下系统稳态误差无法消除的问题,需要引入积分控制.PID 控制的微分函数为[8-9]
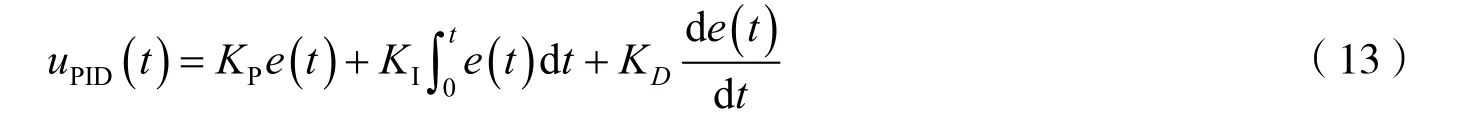
式中:KI为积分系数;uPID(t)为输出信号.磁悬浮小球控制系统在PD 控制基础上引入积分控制后,小球位置的稳态误差为
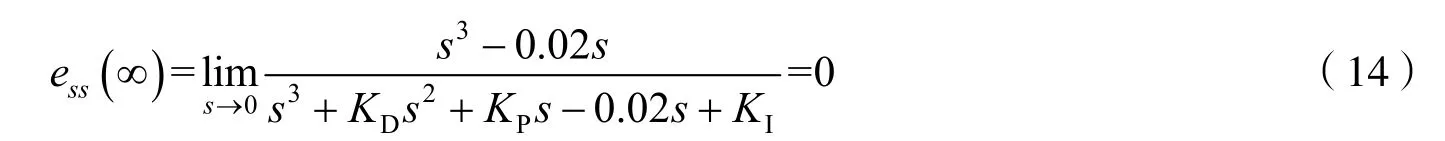
引入积分环节后,可以完全消除系统稳态误差,使小球稳定在平衡位置.在比例系数KP和微分系数KD不变的情况下,积分系数分别取KI=0.01,KI=2时,仿真曲线见图3.当KI太小时,稳态误差消除比较慢,随着KI增大,积分作用加强,稳态误差消除加快;但当KI太大时,系统的超调量增大,振荡加剧,稳定性下降.

图3 KI 参数不同时系统单位阶跃响应曲线
5 结语
本文基于磁悬浮小球控制系统“稳”“快”“准”控制的需求,首次将磁悬浮小球重力控制问题贯穿于PID 控制特性的课堂教学中,将物理问题转化为数学问题,分析PID 控制器的参数变化对系统性能的影响,实现对磁悬浮小球的重力控制.该教学模式能够引导学生以工程需求为牵引,化抽象为具体,调动学生学习积极性,开拓学生的创新性思维,提升学生利用PID 特性分析用于工程实践解决具体问题的能力.

