枢轴量选取对正态总体方差区间估计的影响

王晶，刘彭

（山东农业大学 信息科学与工程学院，山东 泰安 271018）

参数估计方法是基础的统计推断方法之一，此类方法在自然科学和社会科学各领域涉及到数据分析的问题中被大量使用.在实际问题中，人们感兴趣的问题往往与分布族中的未知参数有关.参数估计方法是在总体分布形式已知时，利用样本值对分布中某一个或某几个未知参数值进行统计推断的方法，一般分为点估计和区间估计问题.

在总体分布形式已知时，对于其分布中的未知参数θ，除了求出其点估计外，还希望估计出一个范围，使其以较大可信度包含参数θ的真值.这样的范围通常以区间形式给出，同时还给出其包含参数θ真值的可信程度，这种形式的估计称为参数的区间估计，而这样的区间称为参数θ的置信区间[1].

定义1[2]设总体X的分布中含有未知参数θ,若有来自总体X的一组样本（X1,X2,…,Xn）确定的2个统计量，使得对于给定的α（0＜α＜1），有，则称随机区间是参数θ置信度为1-α的置信区间，分别称为置信下限和置信上限，1-α称为置信度.

在经典统计学中，构造参数θ的置信区间最常用的方法是枢轴量法，其基本步骤可概括为：

Step1选取样本（X1,X2,…,Xn）的一个函数G（X1,X2,…,Xn;θ），其中只含所求置信区间的未知参数θ，且分布已知；

Step2对于给出的置信水平1-α，确定Step1 中分布的双侧分位点λ1，λ2，则有

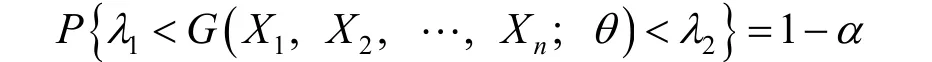
Step3利用不等式变形得到未知参数θ的置信区间.

构造置信区间的方法关键在于Step1 中所选取的函数G（X1,X2,…,Xn;θ）为枢轴量.关于枢轴量，在大部分概率统计教材中对其是这样描述的：选取合适的统计量，要求包括待检验的参数，不含其它任何未知参数，且统计量的分布已知[3]，满足这种要求的统计量即为在区间估计中所谓的枢轴量[4-5].而在参数的区间估计问题中，即使是对同一个未知参数求置信区间，满足以上条件的统计量也往往不是唯一的，此时就面临着如何选取枢轴量的问题.针对选择不同的枢轴量得到的置信区间其性质是否有差别，不同枢轴量下得到的同一参数的置信区间之间是否有优劣之分问题，本文以单个正态分布总体中方差σ2这一参数的区间估计问题为例进行讨论.

1 基于2 种不同枢轴量的正态总体方差区间估计

设总体X～N（μ,σ2），其中总体均值μ已知，（X1,X2,…,Xn）为来自总体容量为n的简单随机样本，则有

式中：X为样本均值.

2 2 种置信区间比较

2 种区间（3）（4）是基于不同枢轴量对单个正态总体方差σ2进行区间估计的结果，若要对其优劣进行比较主要基于可靠度和精度2个指标.在区间估计中，置信度1-α反映的是估计的可靠性程度，置信度越大，估计的可靠性程度也就越大；置信区间的长度反映的是估计的精度，置信区间长度越短，估计的精度也就越高.在样本容量n一定的情况下，这2个要求往往是互相矛盾的[6].在实际应用中，置信度一般按照应用需求直接给定，可靠性已经确定，此时可认为平均长度较小的置信区间精度较高，估计结果更好.

对于置信区间（3），其平均长度为

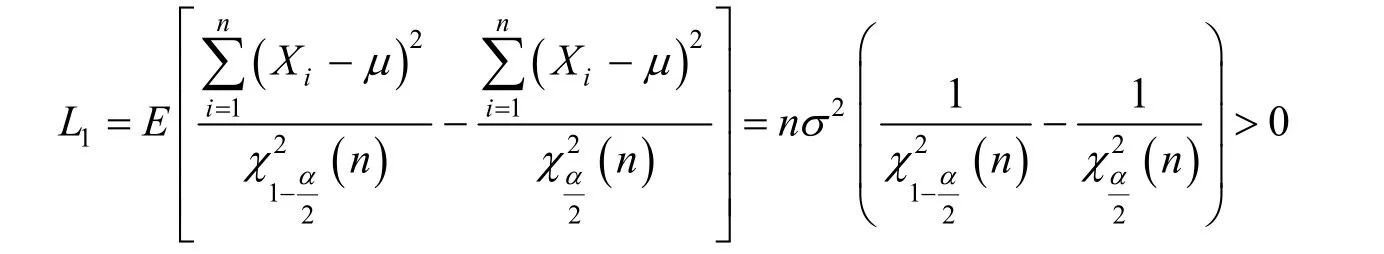
对于置信区间（4），其平均长度为

因此可构造两者比值，其为样本容量n的函数，记为

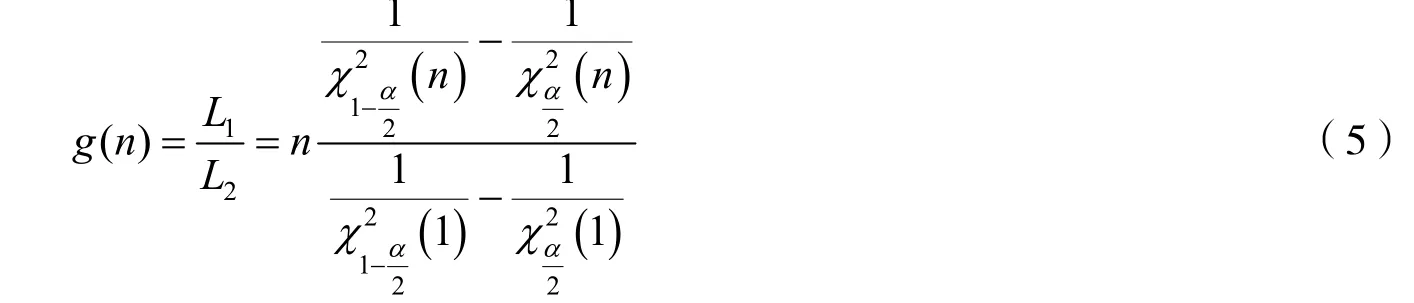
显然n=1 时，，此时L1=L2.当n＞ 1时，g(n)的部分结果见表1（α=0.05）.由表1可见，随着n的增大，置信区间对应g(n) 的差值逐渐减小，即随着样本容量增大，2种置信区间平均长度比逐渐趋于稳定.

表1 不同样本容量下2 种置信区间的平均长度比

在SPSS22.0[7-8]中得到样本容量n∈［1,20］及n∈［1,100］时函数g(n)变化趋势（见图1）.

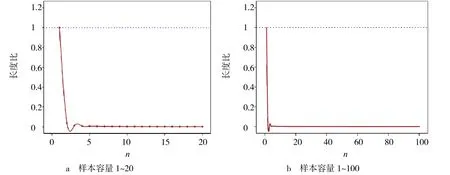
图1 置信区间长度比变化趋势

由表1 和图1可以看出，当n＞ 1时，g(n)的值随着n的增大持续变小，n＞ 5时变化趋于平缓，因此对任意样本容量n，总有g(n) ≤ 1，即L1≤L2，在相同的置信度下，置信区间（3）的精度优于置信区间（4）.在总体均值已知情形下，用枢轴量（3）对单个正态总体的方差σ2进行区间估计效果更好.

为了进一步对结论进行验证，可从特定正态总体中抽样随机模拟获得直观比较结果.设总体X～N(0,1），即参数σ2的真值为1.运用R 软件[9]，从此分布总体中随机抽取100 组容量为n的样本，根据式（3）～（4），由随机抽样结果分别计算σ2置信度为95%的100 个置信区间.n=10，n=100时100个置信区间的模拟结果分别见图2～3.

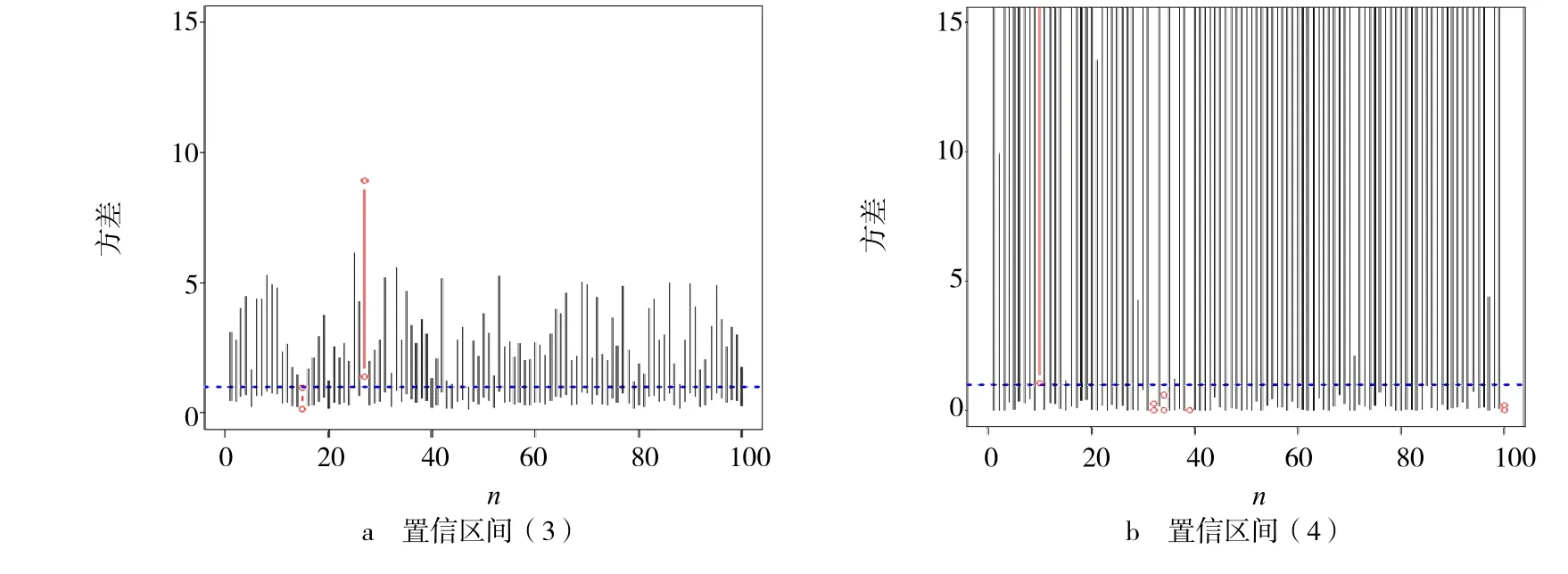
图2 样本容量为10 时的100 个置信区间

图3 样本容量为100 时的100 个置信区间

由图2～3 可以看出，2种情形下均有置信区间（3）的平均长度远小于置信区间（4）的平均长度.相比较下，用枢轴量对单个正态总体的方差σ2进行区间估计，置信区间精度较高，结果更好.

3 实例验证

利用2种方法在总体均值已知情况下，对正态总体方差σ2进行区间估计，通过具体实验结果的计算比较，也能看到置信区间（3）的精度较高.

例[10]发芽期随机抽取某种作物16 株，对株高进行测量，测得株高（单位：cm）数据分别为2.15，2.10，2.12，2.10，2.14，2.11，2.15，2.13，2.13，2.11，2.14，2.13，2.12，2.13，2.10，2.14.求株高标准差σ的95%置信区间（设总体X～N（2,σ2））.

解由实际测量数据，根据式（3）～（4）分别可计算得到株高方差σ2和标准差σ的95%置信区间，结果见表2.

表2 2种不同方法下株高方差和标准差的置信区间

对于该例题，在2种区间估计方法下，具体算得的置信区间差别比较大，显然此例中置信区间（3）的长度远远小于置信区间（4），说明其精度较高.在实际应用中，在可靠度一定的情况下，精度高的置信区间是应该优先选择的，而在经典教科书中对于此类均值已知情形下正态总体方差的区间估计均选用枢轴量进行构造，是有其深刻意义的.可见，枢轴量的选择是有其标准可言的.

4 结语

通过总体均值已知时单个正态分布总体方差σ2参数的区间估计问题，初步阐述了枢轴量的选取标准及其对置信区间结果的影响.在进行置信区间的评价时，可靠性和精度是2个基本标准，而它们也与样本容量n的大小有直接关系，在此不再深入探讨.需要注意的是当考虑置信区间精度这一标准时，应尽量选择区间平均长度小的置信区间.在讨论2种情况下置信区间的平均长度大小关系时，对不同样本容量n的进行了直观模拟.由于比值函数中包含χ2分布分位点，其值为χ2分布的分布函数的反函数值，其取值范围的严格证明仍需要进行更深层次的思考.