推倒一堵墙所需要的力和功

邵云，陶强

（1.南京晓庄学院 电子工程学院，江苏 南京 211171；2.南京市上元中学，江苏 南京 211100）

用力推倒一堵墙在生活中是一个十分常见的事件，但若认真思考，就会发现其中蕴含着不少物理知识.本文将就“力”和“功”2 个方面对其进行一定的解析.

1 推倒均质实心竖墙所需要的力和功

设某一堵均质实心竖墙的厚度为a（见图1），高为H，长为l（图中未显示），密度为ρ，质心在中心C点，右侧的水平推力F距离地面h高度，同时设该竖墙为刚体，它与地面之间的附着应力不构成抵抗因素（实际情况常常如此，见下文），可以忽略，而只有压力，则该堵墙的重力大小为

图1 力推均质实心墙截面示意图

以A点（边）为支点，根据力矩平衡知识有

则推倒该竖墙所需要的起始外力为

将式（1）代入式（3）得

可见，这个起始外力F与墙高H、墙长l成正比，而与墙厚a的平方成正比，与力臂h成反比.当h一定时，随着墙高H的增加，推倒墙所需的外力F也将同比增加，直至∞.

那么，推倒竖墙所需要做的功W是否会随墙高H的增加而趋于∞？

由图1 可知，要想推倒该堵墙，就必须克服墙的重力做功，使得墙的重心C能够到达支点A的正上方，因此，推倒这堵墙所需要做的功至少为

根据图1 有H=atanθ，将它代入式（5）得

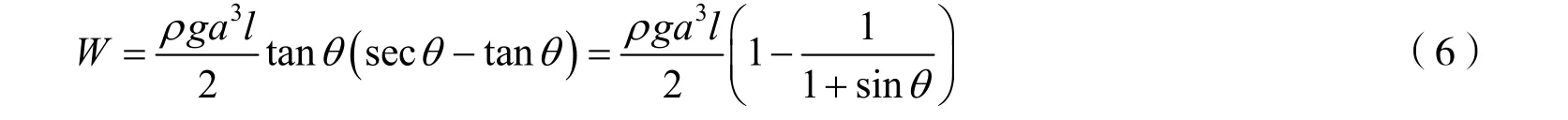
可见，随着墙高H的增加，θ将增加，推倒墙所需要做的功W也将增加.但是W却有个极限值，即当H→∞也即时有

这就是说，推倒无限高的墙所需要做的功并不是无穷大，而是有限值[1].

若墙体是由普通实心砖块建成，其密度ρ=2 ×103kg/m3，设墙长l=10 m，厚度a=0.3 m，则由式（7）可算得推倒无限高此墙所需要的极限功Wlim=1 323 J.这个功其实十分有限，仅相当于把一个67.5 kg的物体举高2 m 而已.

事实上，由式（6）结合图1 即可看出，墙体不用多高，θ角便能接近90°，式（7）所表达的极限功就几乎达到.根据式（5）及墙体参数作出W～H图（见图2），从图2 中可以看出，墙高只需2 m，推倒它所需做的功就几乎等于推倒无限高墙所需做的功.

图2 推倒某面墙所需做的功W 与墙高H 的关系

2 原理分析及思考

从式（4）和式（6）得到了2 个截然不同的结论：当墙的高度H→∞时，推倒墙所需的外力F→∞，但所需的功W却趋于一个定值.该结论出乎意料，通常的直觉是墙越高，推倒它所需要的功“一定同比增加”.究其原因在于，随着墙高H的增加，重力G确实也同比增加，但是推倒墙所需其重心上升的高度却越小（从图1 中的几何关系很容易看出），两者的乘积则趋于一个常量.

由此联想到建高大建筑必须深筑地基且用钢筋浇筑，使地面上、下建筑融为一体，像电线杆一样不易倾倒，同时采用整体的框架结构来扩大建筑的水平有效宽度（相当于本文墙厚a），极大地提升了式（6）（7）中的极限功Wlim（∝a3）值，从而显著地提升了建筑抵抗水平推力的能力.然而，公路旁的围墙通常都是用砖块由平地简单建起（见图3），并未使用钢筋混凝土贯穿地面上下浇筑.由上文可知，它实际上并不太安全，较容易倾倒.因此，当人们经过它时，有必要加以小心，尤其在刮风下雨的天气.

图3 人行道旁的危墙

3 吹倒一面墙所需要的风速

在上文中已经将水平推力F距离地面的高度h视作常量，故而得到所需推力F随墙高H同比增加的结论.实际上，从式（4）可以看出，若F的作用点（即h）随墙高H同比升高，那么所需推力F将保持不变.墙面受到的水平风力便近似属于这种情况，它的作用点近似在墙面中心.

根据空气动力学知识[2-4]，墙长l不很大的平面墙面的风阻系数可以近似视为1，因此墙面受到的风力大小为

式中：ρ空为空气的密度；墙面面积S=lH；v为风速.设ρ空=1.29 kg/m3，风力12 级即风速v=35 m/s，墙高H=5 m，墙长l=10 m，则得

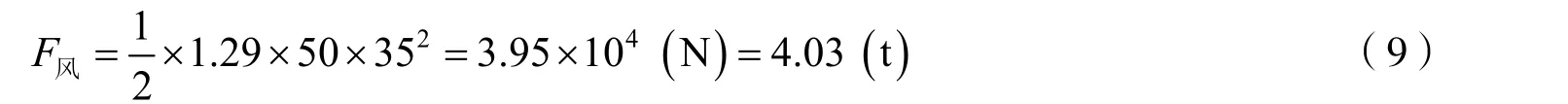
可见该风力十分巨大.

推导吹倒一面墙所需要的风速，将h=H/2代入式（4）即得吹倒一面墙所需要的风力大小

它与H无关.联立式（8）（10）并化简可得

可见，墙越高，吹倒它所需要的风速就越小；反之墙越厚，吹倒它所需要的风速就越大.不难理解，这里的v与墙长l无关.

同样以H=5 m，l=10 m墙为例，并设a=0.3 m，ρ=2 ×103kg/m3，将诸数据代入式（11）可得

经查表[5]，式（12）这个风速相当于9 级烈风（屋顶受损，瓦片吹飞）.类似可算出吹倒H=3 m的矮墙所需要的风速则为30.2 m/s，相当于11级暴风（损毁普遍，房屋吹走）.

这里所得结论的根本原因在于式（10）即F风=ρgla2，吹倒不同高度的墙所需要的风力竟然相等.

4 关于墙与地基之间粘结力影响的讨论

为简化处理，可将墙与地基粘结处的拉伸压缩应力近似看作呈线性分布[6-7]，D为零应力点（见图4）.

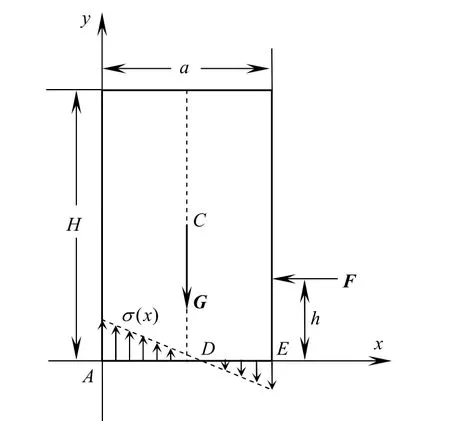
图4 墙与地基粘结处的拉伸压缩应力分布

当重力G与推力F关于A点力矩平衡时，可设应力的分布函数为

于是，根据y方向上的受力平衡以及对A点的力矩平衡有

将式（1）（13）代入式（14）（15），经计算整理可得

联立式（16）（17）解得

再将式（18）（19）代入式（13），即得此时的应力分布函数

右侧墙角E点处的拉伸应力则为

通常建筑材料的抗压性能远优于抗拉性能，因此图4 中墙与地基粘结处的断裂一定是从右侧拉断开始.因此σ(a)即式（22）便成了墙体抵御外界推力的关键.根据式（22）并结合相关数据，可作出σ(a)～H的正比例函数曲线（见图5）.

图5 右侧墙角处的拉伸应力σ（a）随墙高H 的变化

文献[8]指出，普通砂浆粘结的粘土砖墙砌体，沿通缝截面弯曲（类似于推墙）的弯曲抗拉强度规范值约为0.48 MPa.但是文献[9]又指出，若是考虑到实际的施工质量、砂浆质量（包括水泥质量与比例、河砂质量、石屑石灰替代等）、粘结处老化以及裂缝缺陷等因素，整堵墙面的弯曲抗拉强度的设计值大概只能取到规范值的1/3，也即0.16 MPa 左右.于是，对比图5 即可看出，当墙高H＜4 m时，图4 中墙与地基粘结处的拉伸应力确实能够帮助墙面抵御一部分外界推力；但是当墙高H＞4 m时，拉伸应力可能就帮不上忙了——在外力F所产生的力矩尚未与重力矩平衡时，E点处的拉伸应力可能就已经达到了它的设计极限值0.16 MPa.这是由固体内部的应力结构所造成的.

由此可见，本文忽略墙与地基之间粘结力的做法，对于推倒4 m 以下的墙而言，或存在低估，其中对于推力F，从图5 及式（22）可见，墙越矮低估得越多（具体数值读者可以按照上文思路自行建模估算，本文在此省略）；但对于推倒墙体所需要做的功W，则因墙根断裂处的形变极其微小，故而断裂所需要的额外功微乎其微，低估几可忽略.对于推倒4 m 以上的高墙而言，则无“低估推力”之忧，本文的讨论结果完全适用.

5 总结与说明

综上可见，推倒一面与地基之间粘结力几可忽略的老墙、劣质墙或石灰砌墙，所需要的（起始）水平外力F与作用点的位置有关，当作用点的位置固定即图1 中h固定时，F将随墙高H的增加同比增加直至∞；而当作用点的位置也即h随墙高H同比增加时，所需外力F则变成一个常量.水平风力恰好满足后者要求，因此吹倒上述墙所需要的水平风力墙高墙矮都一样，见式（10）即F风=ρgla2，这将导致“墙高招风”——单面墙越高越容易被吹倒.

推倒一面竖墙外力所需要做的功将随墙高H的增加而增加，但是很快就能达到其极限值（见式（6）及图1）.对于通常30 cm 厚的砖墙，推倒2 m 高与推倒无限高所需要做的功几乎相等（见图2）.

推倒一面质量良好的竖墙，对于4 m 以下的墙而言，由于墙根拉伸应力的抵抗作用，所需推力会有所增加，但是所需做的功则几乎没有变化（除非墙太矮）；而对于4 m 以上的高墙而言，由于墙根在外力矩与重力矩尚未达到平衡时就已经断裂，因此墙根处的应力对于推倒高墙不构成任何影响，无论所需外力还是功.

本文作为模型计算，目的并不在于具体的数值，而是在于揭示总体的规律性，为人们的日常生活及教学提供一些参考.从较深入的研究结果看，除了对于4 m 以下质量良好的墙体外，本文开始时“竖墙与地面之间的附着力不构成抵抗因素，可以忽略”的假设基本是合理的.