地表水力特性对植被过滤带中胶体迁移的影响
孙小璐,庾从蓉,2,孙钰峰
(1.河海大学 水文水资源学院,南京 210098; 2.水文水资源与水利工程科学国家重点实验室, 南京 210098)
1 研究背景
面源污染已成为地表水环境中最主要的污染源[1]。面源污染中常含有大量的胶体物质(直径<10 μm的颗粒物),由于胶体物质既具有以水体速率在土壤、地表中运移的溶解相特性,又具有吸附其他污染物的类似固相基质特性[2],很容易作为污染物的载体改变污染物原有的运动速率和运动范围。目前,植被过滤带(Vegetative Filter Strips,VFS)被视为防治面源污染应用最广、效果最好的措施之一[3-6],对泥沙[7]、氮磷[8]、胶体[9-10]以及微量元素[11]等污染物有较好的截留效果,因此研究胶体的运移规律对控制面源污染具有重大的工程意义。
目前研究胶体在VFS中的迁移规律主要基于胶体与多孔介质相互作用基本理论——胶体过滤理论(Colloid Filtration Theory, CFT),该理论广泛应用于地下水,描述外部条件变化(流速、胶体粒径、介质粒径、液体黏滞系数等)对胶体在多孔介质迁移过程中的影响。在多孔介质中,如地下水,水流速度非常缓慢,雷诺数低,水力特性对胶体的迁移影响不显著。该理论描述胶体沉积吸附在多孔介质上,表现为直接捕获(direct interception)、惯性撞击(inertial impaction)、扩散沉降(diffusional deposition)和重力沉降(gravitational deposition)4种形式[12]。但通过VFS的水流,流速快且植物的茎和枝把水流动能转变为湍流动能,增加了水流的流态和雷诺数。水力特性的改变也影响了胶体在VFS中的迁移沉积特性。将VFS对胶体的直接捕获作用分为2个步骤:①胶体和植物发生接触(用接触效率η0表示,即胶体与植物发生接触的速率与流向植物的胶体速率的比值);②胶体与植物接触后成功地附着在植物上(用附着效率α表示,即胶体成功附着在植物上的速率与胶体与植物发生接触的速率比值)。这样植株对胶体的直接捕获效率η表示为接触效率η0和附着效率α的乘积,即η=η0α。Palmer等[13]针对水生系统中常见流态(1≤Re≤1 000),对悬浮颗粒物在单个圆柱上的沉积作用的研究发现,当水流的雷诺数为50 本文利用仿真草模拟植被,构造饱和下垫面和降雨条件的VFS,并利用数值模型模拟胶体在不同雷诺数水流VFS中的迁移沉积状况,将胶体在VFS传输过程中的宏观迁移沉积现象和微观机理结合,探讨降雨径流雷诺数在50~500范围变化时,VFS中胶体的迁移机理、去除方式及去除效率。 本研究选用常见高岭土模拟胶体颗粒物,高岭土胶体在震荡静置7 h后粒径均匀且稳定性更高[17]。将20 g高岭土(天津市福晨化学试剂厂)粉末放入2 L去离子水中,使用磁力搅拌器搅拌均匀后,用紫外超声波振动器振动30 min,之后在室温下静置7 h,最后取1 L上层清液作为试验用胶体悬浮液,再测量胶体初始浓度。共15次试验的初始浓度基本一致(配置存在操作误差,有微小差异),平均初始浓度为3 319.8 ppm,初始浓度相对标准偏差为6.00%,所得胶体粒径约为2 μm。用尤加利叶仿真草模拟VFS,其具有绿色环保、密度可控和经济实用的特点,且柔韧性和强度适中,能代表径流中普遍植被形态。试验选取石英砂作为砂土的代表。石英砂购于南京宁磊石粉加工厂,石英砂直径在0.8 mm左右,由于石英砂多呈不规则形态,因此土层孔隙度在50%左右。 本研究中设计和制作了一个矩形有机玻璃水槽9.6 m×0.6 m×0.25 m(长×宽×高),并在水槽底部铺设约20 cm厚的石英砂,石英砂表面铺设尤加利叶仿真草,密度为1 715棵/m2,植株高度为8 cm。试验装置分为4个部分:降雨系统、入流控制系统、水槽主体、排水与尾水监测系统(图1)。其中降雨系统采用NLJY-10型人工模拟降雨系统,由南京南林电子科技有限公司进行设计施工。降雨设备尺寸为9 m×1.2 m×3 m(长×宽×高),主体为相连通的铜管,保证降雨装置中各部分压强相同,每个喷头流出水量相同。在水槽主体正上方中间分布有7组喷头,每组含3个喷头,以实现降雨均匀覆盖水槽主体。试验过程中降雨均匀度系数>0.81,有效降雨面积完整覆盖水槽主体。 图1 试验装置示意图Fig.1 Schematic diagram of experiment device 试验设计通过控制入流流量达到改变水力特性的效果,雷诺数经验计算公式为 Re=Udc/ν。 (1) 式中:U为试验平均流速(m/s);dc为收集器直径(m);ν为水的运动黏度(m2/s),本文选择常温25 ℃下对应的运动黏度(ν=0.897×10-6m2/s)。 通过调节流量控制流速至预计雷诺数,预试验中需要确定流速-沿程水位-雷诺数的关系。前人研究河流中植物对水流水力特性影响时,一般把植株简化为圆柱体[18-19]。针对胶体迁移过程的研究,也认为圆柱体近似于自然收集体(芦苇、互花米草等)[13],可以准确模拟胶体在植株上的沉积吸附过程[20-21]。考虑到植被的垂向形状变化对水流结构的影响明显,本文结合垂向植株(由茎向冠)的变化趋势,提出将单株植株(茎、枝和叶)概化为直径线性变化的圆柱体(圆台),即植株由茎向冠,圆柱的直径呈线性增加的趋势。该概化方式简洁地模拟了径流中植株对水流的扰动影响,且准确地描述了径流水位变化时植株对径流水力特性所造成的影响,以及试验中dc由单株尤加利叶仿真草的直径决定。当植株正常放置于水槽中时,垂直高度1.5 cm处开始均匀分布叶片,且上部叶片相互交错。在位置i处,当径流水深hi≤1.5 cm时,取d1(单株植株最小直径)=6 mm;当径流水深hi≥8 cm时(完全淹没植株),经测量,取d2(单株植株最大直径)=40 mm。植株整体dc由d1、d2加权平均决定,即为:当hi>1.5 cm时,dci=[(hi-1.5)×40+1.5×6]/hi;当hi≤1.5 cm时,dci=6 mm。 根据试验经验,选择雷诺数分别约为50、150、250、350和450,但由于入流水泵的开度存在控制误差,经过校正,最后确定本试验控制入流流量为0、275.04、672.48、1 013.04、1 463.76 L/h,对应雷诺数分别为65、146、258、315、486(表1)。试验中水位/沿程水深通过在沿程控制断面处左侧、中部和右侧分别用直尺竖直向下测量水深,以入流流量除以8 m控制断面处地表径流的截面面积(水深×水槽宽)代表8 m内平均流速。每个工况试验进行3次重复。 表1 试验工况Table 1 Test conditions 试验步骤如下: (1)准备。打开进水系统,待砂层饱和(观测到尾水槽中三角流量堰水位稳定),打开降雨系统,设置降雨模式为大雨(降雨强度为66.7 mm/h)。 (2)放样。将制备好的胶体悬浮液在0 m断面处瞬时地、沿断面均匀地一次性倒入水槽,并开始计时。 (3)采样。在1、2、4、8 m断面处采集样品,每断面均匀选取3个位置(左侧、中间、右侧)各采集1个样品,通过3个样品浓度均值反映断面平均浓度。使用10 mL离心管进行采样,每个样品水量>5 mL。 (4)测样。样品在采集后立即测量,样品经轻轻震荡、润洗比色皿后,倒入比色皿中,用紫外分光光度计测量样品吸光度,经标准曲线换算,获得样品浓度,记录各样品的位置、时间和浓度数据。 模拟胶体在饱和VFS中运移的模型主要分为2个部分:VFS中的降雨产流模型和胶体运移模型。通过Wolfram Mathematica软件建立模型并模拟计算。 2.3.1 水量平衡方程 本文参考Konstadinos等推算出的福克海默近似解析解[22],构建了水量平衡方程,其公式如下: (2) (3) (4) h=h0,x=L。 (5) 式中:H为入流水量引起的水层厚度(m);q为达西流速(m/min);R为降雨强度(m/h);h为沿水流方向水深变化(m);x为距离(m);W为试验水槽宽度(m);Q为前端入流流量(L/h);L为试验水槽长度(m);a、b为常数;h0为末端水深(m)。 本试验中,同种试验条件下H、R、W、L、Q均为已知。式(4)、式(5)共同描述试验中水流的边界条件,即在0 m断面处为入流流量,在8 m断面处,尾部地表径流自由出流。 2.3.2 胶体运移模型 胶体随径流的运动,主要包括水平维度和垂直维度的传输[23]。水平维度中胶体随地表径流迁移过程中在植株上发生吸附沉积;在垂直维度中由于径流和土壤水中胶体浓度差的存在,胶体在浓度梯度驱动下产生扩散过程。胶体在饱和植被过滤带迁移的概念模型如图2所示。 图2 胶体运动过程简图Fig.2 Schematic diagram of the process of colloidal movement 胶体运移方程如下: (6) (7) 式中:C1为地表水中溶质的浓度(mg/L);t为时间(min);C2为土壤水中溶质的浓度(mg/L);D为胶体在地表水中的扩散系数,表示为地表水中水平扩散系数(m2/min);x为地表水流方向距离(m);kd为高岭土沉积吸附效率系数(min-1);B为地表水层厚度(m);y为垂向距离(m);D*为胶体在流速干扰下向土壤水扩散系数,表示为地表水中垂直扩散系数(m2/min)。 在径流向土壤水扩散过程中,始终由高浓度侧向低浓度侧扩散,在土层扩散过程中,由于土层处于饱和状态,不存在非饱和侧向流动,且采样时间较短,因此忽略胶体在土壤水中的横向扩散,即仅考虑在土壤中胶体发生垂直方向扩散。垂直方向中,以水土交界面作为基准面,即水土交界面表示为y=0。据此,设定边界条件为 (8) 利用Wolfram Mathematica软件的ND Solve指令运算式(6)—式(8),可根据参数kd、D对胶体在各控制断面的实测渗透曲线进行初步模拟,并使用该软件的Find Fit指令求解该实测渗透曲线的最优参数组合。过程中参考由非线性最小二乘参数优化方法计算出的模拟值和试验值的最小化误差和,即可得参数kd、D的最优解。 胶体在不同水力特性、不同雷诺数(65、146、258、315、486)的地表径流中迁移至1、2、4、8 m处的穿透曲线见图3。观测浓度值C,通过初始浓度值C0进行归一化处理(C/C0)。观测点代表每种工况下3次重复试验的平均值,误差线代表重复试验的标准差。穿透曲线是各控断面处,不同时间点的相对浓度值,反映胶体浓度在各断面处随时间的变化过程,峰面面积反映各控制断面通过胶体总量。当雷诺数为65时,由于VFS的入流量为0,地表径流水位太低,没有稳定水位观测值,不满足模型模拟条件;雷诺数为146时,水槽中优先流现象导致坡面地表径流不均匀,径流模型运算不稳定、误差较大(图3中(a)和(b)只有实测值)。地表径流的雷诺数在258~486之间时,坡面流均匀,模型模拟效果佳(图3中的(c)、(d)、(e)),参数模拟结果的纳什效率系数均≥0.95(表2)。 图3 不同雷诺数条件下胶体观测-模拟浓度穿透曲线Fig.3 Breakthrough curves of test-simulated concentration of colloid at various flow rates 表2 各流速条件下高岭土胶体的参数模拟结果Table 2 Summary of simulation results of Kaolin colloid parameters under various flow rates 除图3(a)地表径流为降雨产流外,其他水力特性的地表径流中,胶体在各断面的穿透曲线均呈正态分布,随着迁移距离的增加,穿透曲线形状由高瘦型逐渐转变为矮胖型。随雷诺数的增大,由于流量增大,降雨的稀释作用与胶体扩散作用增强,相同断面胶体的峰值(1 m:0.20~0.074;2 m:0.169~0.054;4 m:0.052~0.037;8 m:0.028~0.024)均明显降低。 根据模型计算,模型参数D、kd变化趋势基本一致(图4),具体表现为两点:①随雷诺数增大,D、kd在各控制断面有增大趋势;②同一水力特性条件下,D、kd沿程减小。 图4 不同雷诺数条件下模型参数D、kd沿程变化Fig.4 Variation of model parameter D and kd under various velocity conditions 3.2.1 雷诺数增大,D、kd在各控制断面均增大 从水力特性变化分析,在黏性流体绕圆柱体流动时,随流体雷诺数的增加,圆柱体背部尾流表现出的流动特征如下:当5≤Re≤15和Re<40时,存在稳定的、对称分布的一对立式旋涡,附着在植株茎的后部,见图5(a);当40≤Re<150时,随Re增大旋涡出现有序的层状脱落,在植株茎的尾流中形成依次发放的涡街, 见图5(b);当150≤Re,尾流开始出现湍流效应;当Re=300,尾流湍流现象明显;当300 图5 5≤Re≤15,Re<40和40≤Re<150流线示意图[24]Fig.5 Streamlines when 5≤Re≤15,Re<40 and 40≤Re<150[24] 在本文研究雷诺数47≤Re≤500区间范围内,随着雷诺数的增大,水流中从稳定的漩涡到形成漩涡脱落[24],流场转变为震荡流场,且漩涡脱落规律性降低。一方面,使得植株上游侧胶体捕获窗口变宽,另一方面,扩大了植株背面沉积吸附位点,增加胶体在植株下游侧的沉积。Purich[15]利用表面涂有油脂的塑料棒(d=0.6 cm,h=16 cm)阵列模拟植被,当Re在235~640间逐渐增大,塑料棒背面沉积吸附量增加约2倍。 依据胶体过滤理论,胶体在收集体上的沉积吸附过程可以分为直接捕获、扩散捕获以及沉淀捕获。在本文水流状态下胶体颗粒物的沉积形式主要为直接捕获,本文只考虑直接捕获,忽略其他2种方式。针对悬浮颗粒物在单个光滑圆柱体收集体(模拟植被)的沉积研究中,建立了直接捕获效率η与圆柱体收集体雷诺数Re、粒径比Rc(粒径比表示胶体粒径与收集直径(dc,针对收集体为圆柱体)之比)的经验公式(η=0.224(Re)0.718(Rc)2.08)。该经验公式粒径比变化区间为0.86×10-4~0.031,在柱状分叉结构中,有良好的运用。本文中胶体粒径通过测量约为2 μm。虽然本文研究对象是片状收集体,但粒径比在此范围内,在我们将来的研究中也可以参考应用,在η~(Re)m(Rc)n关系中,经验系数m、n的值有待确定,但可推测该关系依然成立。在该研究中,假设所有的粒子-收集体接触都会导致粒子捕获(即α视为1),又有η=η0α,因此直接捕获效率η与接触效率η0相等。由于附着效率α主要受离子强度、离子种类和表面电荷密度等系统内化学条件的影响,本文试验中α可视为保持稳定,因此接触效率η0增大将表现为直接捕获效率η增大。所以有直接捕获效率η随雷诺数增大而增加,胶体的吸附沉积过程增强。 3.2.2 同一水力特性条件下,D、kd沿程减小 分析图3胶体沿程穿透曲线变化,胶体运移过程中随距离增加,胶体的相对浓度值C/C0逐渐降低。胶体运移过程由于沉积吸附过程、扩散过程,胶体浓度显著降低,使胶体整体表现出扩散量、扩散范围降低,扩散系数D减小。 由于电位、粒径等物质本身特性与流速变化无直接关系,于是只选用一组试验胶体,利用DelsaMax PRO Zeta电位与纳米粒径同步分析仪,测量VFS中尤加利叶仿真草、砂土、胶体的表面电势(表3)及沿程胶体的粒径、表面电势(表4)。 表3 胶体沿程粒径、表面电势变化Table 3 Particle sizes and surface potentials of colloid along the flow 表4 仿真草、砂土和胶体母液的表面电势Table 4 Surface potentials of simulation grass, sand and colloid’s mother solution 由表3可知试验中胶体有粒径沿程增大、表面电势沿程减小的趋势。粒径较小的胶体表面电势小,而且布朗运动更剧烈,沉积过程和扩散进入砂土过程更为明显。由于胶体的异质性,沿程运移过程中胶体颗粒与植被、土壤沉积过程发生概率不同,产生分选作用,使得胶体表现出的特性发生变化。由表4可知尤加利叶仿真草、砂土、胶体母液表面电势均为负电性,表明胶体吸附过程中始终处于不利吸附条件。结合DLVO理论,在不利吸附条件时,胶体与收集器之间的相互作用力取决于表面电势。表面电势绝对值越小,两者间静电斥力越小,总相互作用能为负,即对应第二能量势阱越深,胶体更容易被吸附[27]。本研究中由于表面电势绝对值小的胶体更容易沉积在植被表面,胶体中表面电势绝对值大的颗粒比例增大,沿程胶体表面电势绝对值有增大趋势,导致胶体与植被间第二能量势阱变浅,沉积吸附能力减弱。 随地表径流雷诺数的增加,胶体在植被上的沉积吸附效率增强,但是饱和VFS对地表径流中胶体的去除效率P却降低(图6)。 图6 各控制断面的去除效率随雷诺数变化情况Fig.6 Removal of colloid in each control section varying with Reynolds number 胶体在饱和VFS中的迁移过程包括水平维度、垂直维度2个方向。水平维度中主要表现为胶体在沿程VFS上的沉积吸附作用,垂直维度中主要表现为在浓度梯度的驱使下,胶体由地表径流扩散至饱和土壤水中。假设胶体向土壤水扩散系数D*随流速增加保持不变,但伴随着雷诺数的增加,地表径流流速也增大,从而减少了地表水中的高浓度胶体与土壤交界面的接触时间,同时由于后续无持续高浓度胶体与土壤界面接触,导致胶体扩散至土壤水中的量减少。本试验未模拟入渗,但通过分析表明,雷诺数增大过程中,胶体回收率(去除效率)与雷诺数变化呈正相关,胶体沉积吸附效率系数与雷诺数变化也呈正相关,可见胶体沉积吸附作用与总体去除效率P变化趋势相反,因此水平维度胶体在沿程VFS上的沉积作用不是胶体去除的主要方式。垂直维度中胶体由地表径流向饱和土壤水的扩散作用为胶体去除的主导机制。 通过构建室内饱和植被过滤带数值模型,探究降雨条件下地表径流水流特性对胶体在饱和植被过滤带中迁移、沉积的影响,得到以下结论: (1)随雷诺数增大,植被中绕流状态逐渐复杂,复杂的流态通过增强胶体在植株下游侧的沉积,以及增大胶体的直接捕获效率,最终增加了胶体在植被上的沉积吸附过程。 (2)同一水力特性条件下,由于胶体的异质性以及造成的分选作用,胶体沿迁移距离的增加,粒径增大、表面电势减小,沉积吸附能力沿迁移距离的增加而减弱。 (3)土壤饱和状态下,随着雷诺数增大,胶体滞留时间缩短,胶体在VFS中的去除效率降低。胶体向土壤扩散为VFS中胶体去除的主要方式。2 材料与方法
2.1 材料与装置
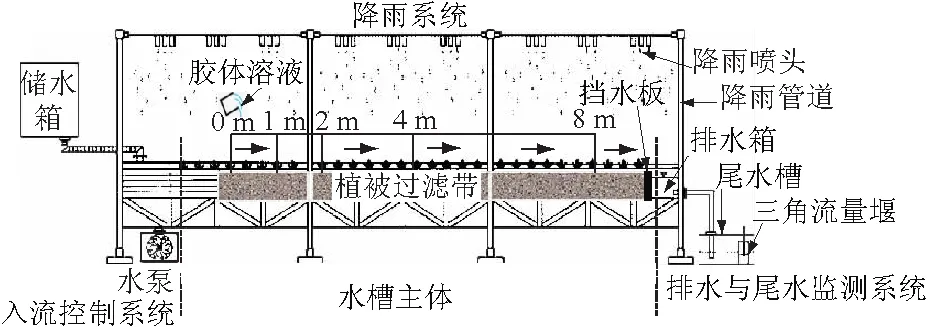
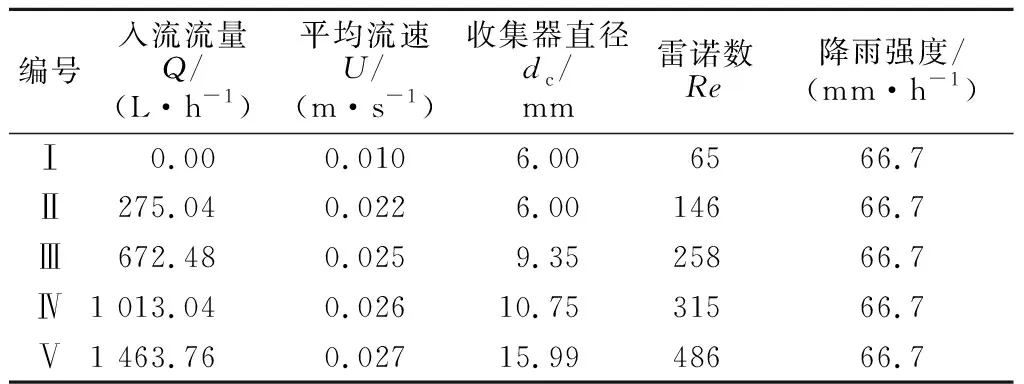
2.2 试验工况与步骤
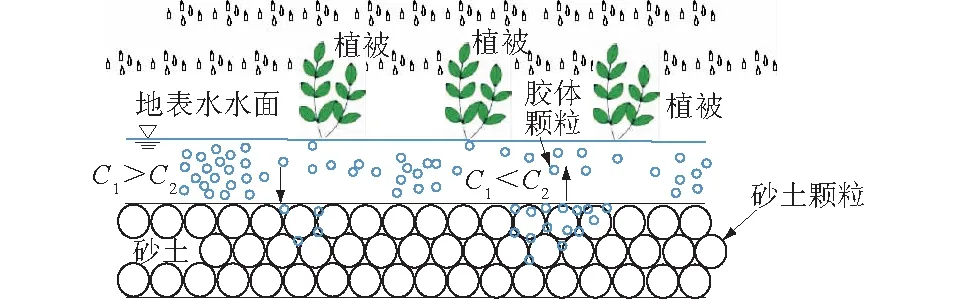
2.3 数值模型的建立

3 结果与讨论
3.1 不同水力特性地表径流中胶体在植被过滤带中的穿透曲线
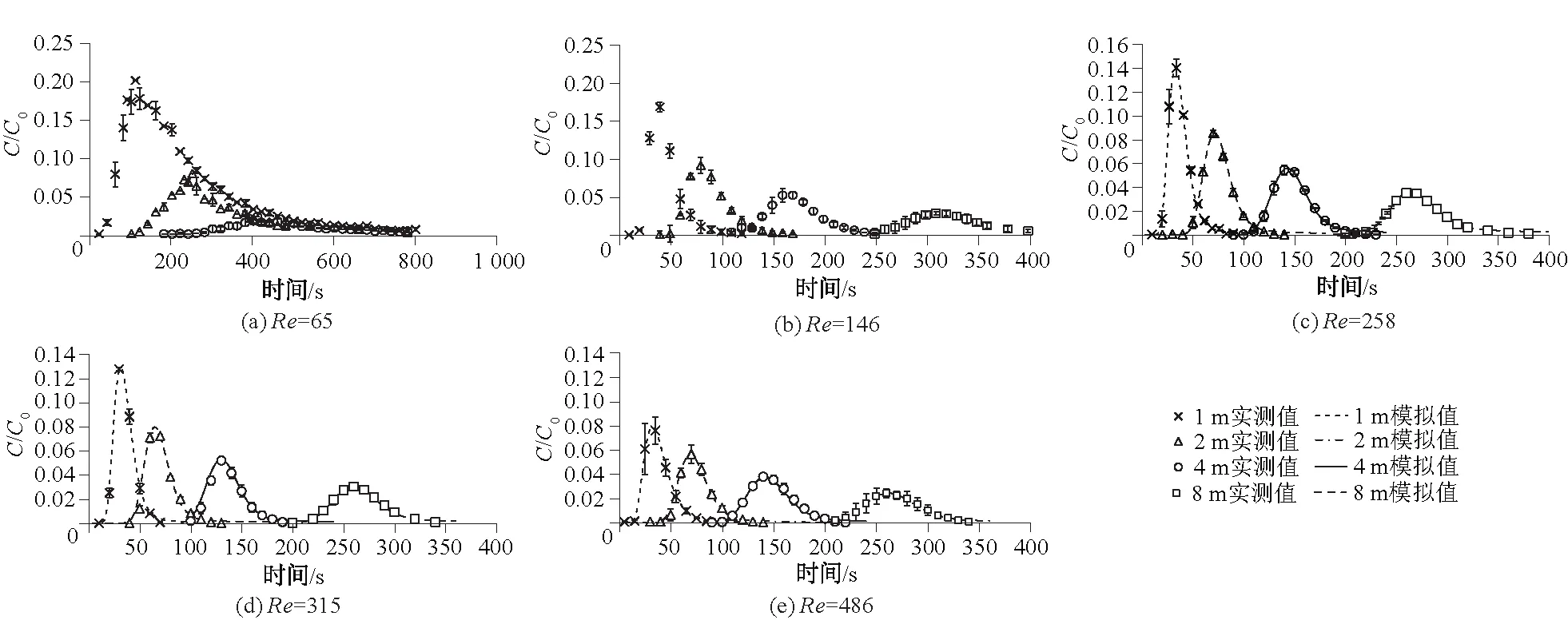
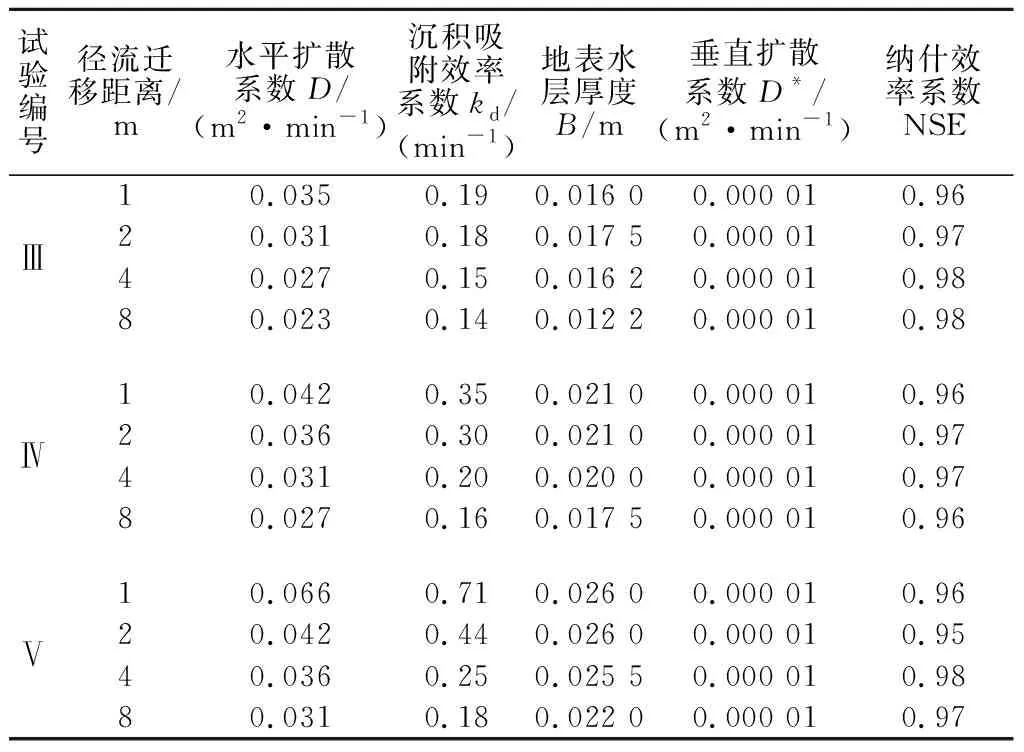
3.2 地表径流水力特性对胶体在植被上沉积的影响
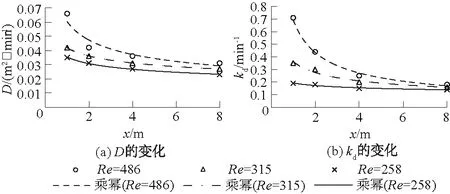
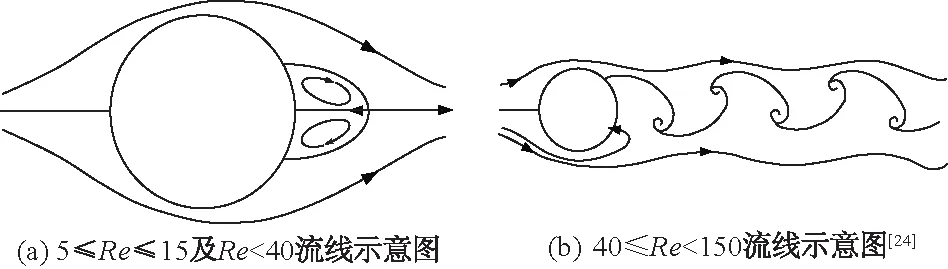


3.3 地表径流水力特性对胶体去除效率的影响
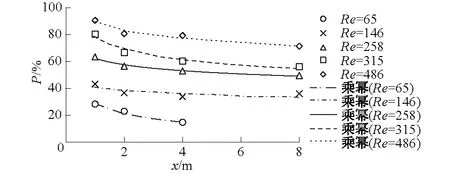
4 结 论

