软土变形指标与初始孔隙率的相关性分析

李雪梅，杨 敏，李卫超，上官士青，万嘉成

(1.同济大学 土木工程学院，上海 200092； 2.中交公路规划设计院有限公司上海分公司，上海 200092；3.同济大学 建筑设计研究院(集团)有限公司，上海 200092)

1 研究背景

基于临界状态土力学下建立的修正剑桥模型在岩土工程中有着广泛的应用，其中的模型参数λ是等向压缩试验的临界状态线在e-lnp′平面中的斜率，κ是正常固结土在等向回弹试验下卸载曲线在e-lnp′平面上的斜率。通过数学转换可得如下关系式：

λ=C′c/2.303 ;

(1)

κ=C′s/2.303 。

(2)

式中：C′c、C′s分别为等向压缩与回弹试验中压缩和回弹曲线在e-lgp′平面中的斜率[1-3]。但实际工程实践中，综合考虑工程结构安全可行、时间及经济等成本，很少开展等向压缩回弹试验，而是基于工程中常用的一维压缩回弹试验得到的压缩指数Cc和回弹指数Cs值估算对应的λ和κ。目前，国内外对等向和一维压缩回弹试验下的压缩指数与回弹指数值及二者之间的关系研究相对较少，且对基于一维试验得到的压缩指数和回弹指数估算修正剑桥模型参数λ和κ值的可靠性并没有统一的结论[4-6]。

压缩指数和回弹指数是表征土体变形特性的2个重要指标参数，而获得这些参数最可靠的途径就是开展土的固结试验，然后通过压缩和回弹指数得到对应的理论模型参数，但试验比较费时费力，且有些情况下很难有立即开展试验的条件。而大量的试验研究和统计结果发现，土的模型参数与土的物理性质指标之间具有很强的相关性，且对于软黏土而言，选择的物理指标主要集中在能够反映软土工程特性的天然含水率wn、孔隙比e0、液限wL和塑性指数Ip等。比如，Skempton[7]就发现原状土样和重塑土的压缩指数Cc与液限wL之间存在较好的相关性，该结论后来也得到了工程实践的进一步证实。Terzaghi等[8]用wn代替wL提出Cc与wn之间的关系式。Azzouz等[9]对700多个土样进行统计分析发现，与压缩指数Cc相关性较好的物理指标是wn和e0，其次为wL，且相对于采用单独的指标，多个物理指标参数联合的关系式的拟合效果并不会明显提高。通过对韩国东、南、西海岸1 200个土样进行单参数和多参数的相关性分析，Azzouz等[9]与Yoon等[10]得出的结论一致，即多参数并不能进一步提高压缩指数Cc与物理指标之间的拟合效果。柯文汇等[11]研究了结构性软黏土一维压缩变形特性与物理指标之前的数学关系。Nakase等[4]对重塑和原状黏土进行了一系列三轴和固结试验，建立了Cc与Ip之间的线性关系，针对搜集的饱和软黏土的试验数据，白冰等[12]也给出了Cc与Ip的经验关系。以上均是关于Cc与物理指标之间的关系，而关于回弹指数的讨论相对较少。因此，如何通过土体的基本物理性质指标(如天然含水率wn、孔隙比e0、液限wL和塑性指数Ip)估算模型参数是一项重要的研究内容。

研究人员在大规模的工程建设中积累关于上海软黏土丰富的研究资料，主要包括：第②层粉质黏土、第③层淤泥质粉质黏土、第④层淤泥质黏土、第⑤层粉质黏土，其中第③、④层为典型的软土。魏道垛等[13]对上海浅部土的应力历史的分析表明，上海地区第②层土为超固结土，而第③—⑤层基本可作为正常固结土考虑。Gao等[14]对上海地区浅部土进行了室内和原位试验，结果表明上海浅部黏土层位分布规律比较强，且Cc与物理指标之间存在着比较密切的相关性。近几年，针对上海软土物理力学性质特性的研究建立了Cc与天然含水率wn、初始孔隙比e0之间的关系，但不同的研究者给出的关系式仍存在一定的差异[15-16]。需要强调的是，这些研究均是基于一维固结压缩回弹试验结果，建立了一维条件下软土变形指标与物理性质指标的关系，鲜有基于等向压缩回弹试验结果得到的变形指标方面的研究，尤其是针对上海地区。

基于以上分析，本文针对上海地区不同深度软土的原状土样进行一维和等向压缩回弹试验，得到各自的压缩和回弹曲线。首先根据试验结果，得出对应的压缩回弹指数，其次讨论了不同试验条件下压缩与回弹指数与修正剑桥模型参数λ与κ之间的关系，并建立其与物理指标之间的相关性，得到对应的关系式。除本文开展的试验数据外，本文作者进一步搜集了我国沿海地区针对软土的相关试验数据，进一步建立了压缩指数与初始孔隙率之间的关系，并得到可适用于我国沿海大部分地区(广州、天津、深圳、温州、福州等)软土压缩指数计算的经验关系式。

2 一维和等向固结试验

2.1 土样物理性质

试验土样是上海地区典型的第②—第⑤层原状黏土，根据《土工试验方法标准》[17]与《岩土工程勘察规范》[18]进行一系列的室内试验，得到其基本物理性质指标如表1所示。图1给出了各层土的塑性图的位置[19]。如图1所示，各土样均位于A线上侧，B线左侧，属于低液限黏土。

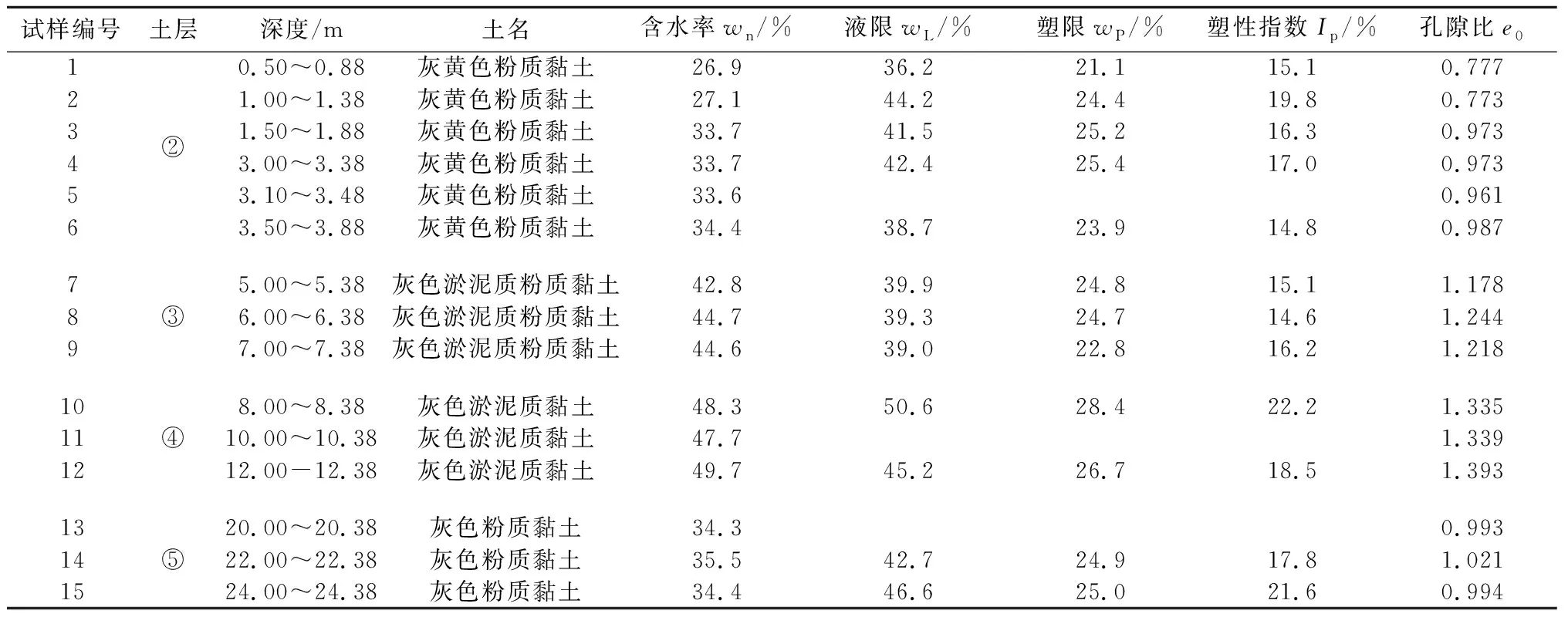
表1 土的物理性质Table 1 Physical properties of Shanghai clay samples

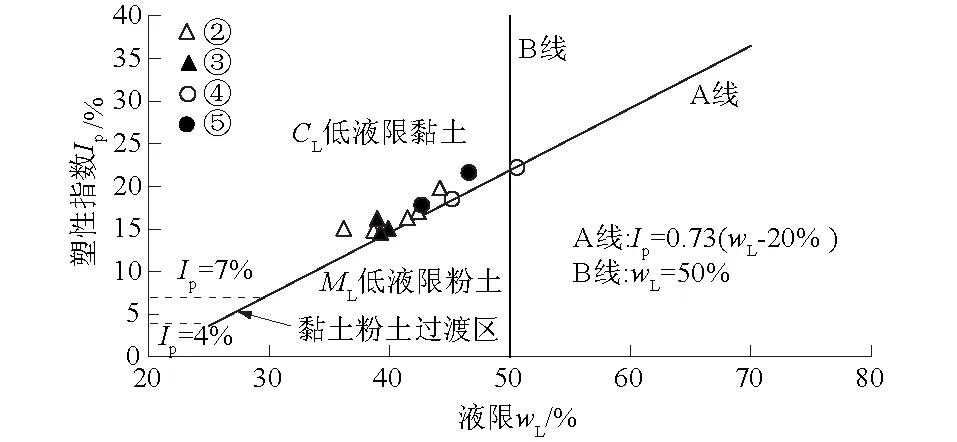
图1 上海浅部各层黏土在塑性图中的位置Fig.1 Plasticity chart of Shanghai clay samples of different layers

2.2 试验方法

一维固结试验采用GDS等梯度固结仪，环刀高22 mm、直径63.5 mm，采用分级加载，加载顺序为加载-回弹-再加载。为了避免荷载大小和加荷比的不同对试验结果的影响，加荷比均为1.0，固结压力25～1 600 kPa，在200、800、1 600 kPa压力下进行3次回弹试验，具体加载过程如图2所示，固结稳定标准为变形<0.005 mm/h。

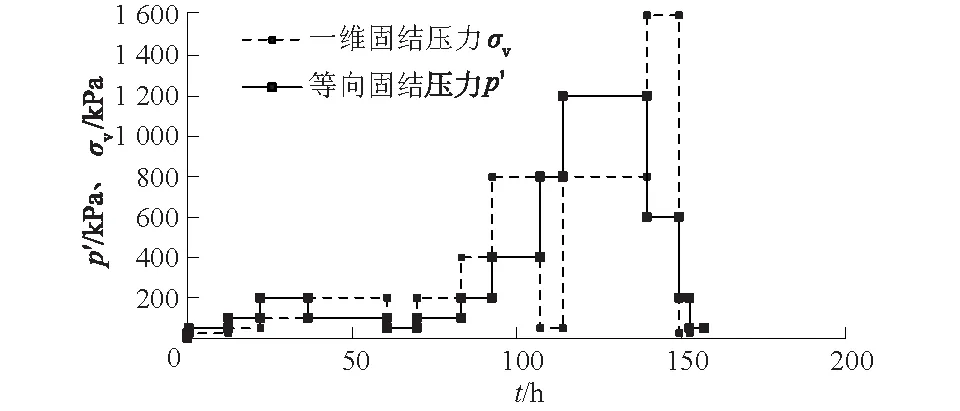
图2 一维固结和等向固结试验的试验方案Fig.2 Load steps of one-dimensional consolidation and isotropic consolidation

等向固结试验采用GDS应力路径三轴仪，试验尺寸与三轴试验相同，即高80 mm、直径39.1 mm的圆柱样。切好的试验土样装入压力室后，进行反压饱和，当Skempton系数B>0.96后，认为饱和完成，随后开始等向压缩、回弹试验。加载方案如图2所示，压力25～1 200 kPa，在200 kPa和1 200 kPa压力下分别进行回弹再压缩，加荷比为1.0，每级压力下的稳定标准为每5 min内的排水量<5 mm3。

2.3 试验结果分析

根据一维和等向固结试验结果整理分析，通过绘制对数坐标下的e-p曲线图的方式得到2种试验条件下Cc和Cs的值。图3给出了土样12分别在一维和等向压缩、回弹试验条件下得到的对数坐标下的e-σv(p′)曲线，根据该曲线得到加、卸载直线段的斜率，得到一维和等向固结试验下的Cc和Cs。采用同样的方法，得到表2中各土样的压缩与回弹指数值，见表2。

图3 上海第④层土固结曲线Fig.3 Consolidation curves of Shanghai undisturbed clay samples of layer ④

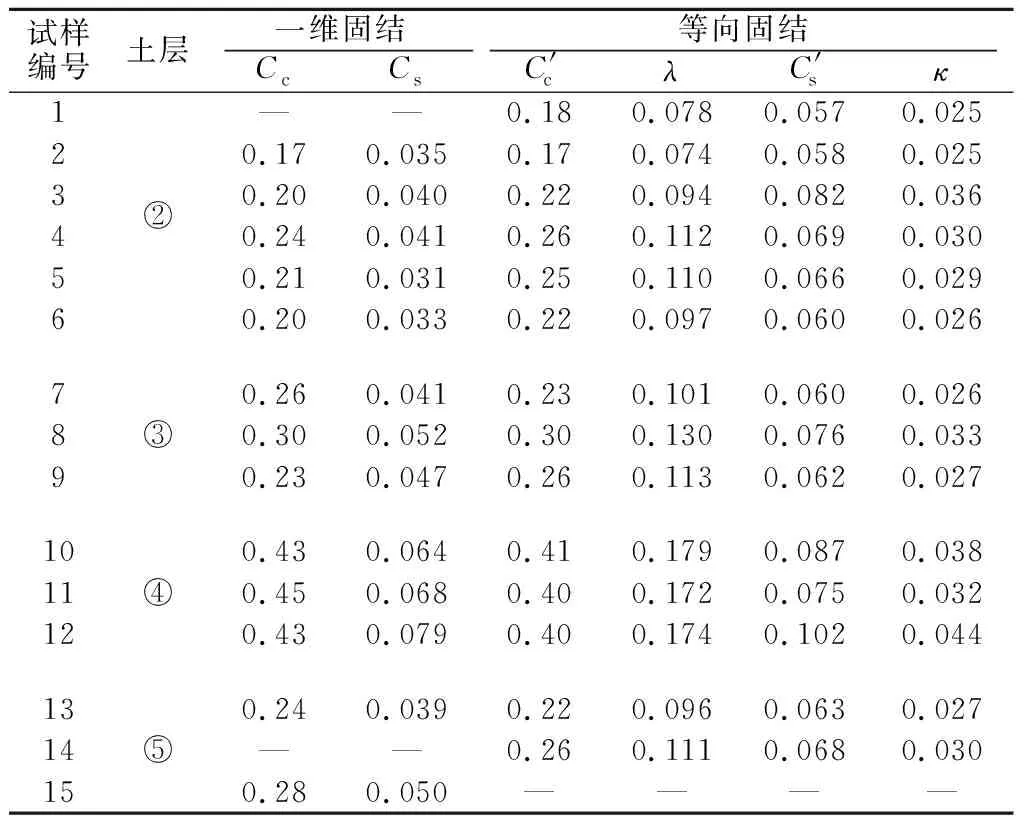
表2 一维和等向固结试验结果Table 2 Results of one-dimensional consolidation and isotropic consolidation

图4(a)给出了修正剑桥模型参数λ分别与一维和等向固结试验下的压缩指数Cc、C′c之间的关系。如图4(a)所示λ与Cc之间存在较好的线性关系，即

λ=Cc/2.351 。

(3)

决定系数R2为0.92，且式(3)与式(1)基本重合，故工程实践中采用一维固结试验下的压缩指数Cc来代替等向固结试验下的C′c计算模型参数λ，其结果是可靠的，即等向固结试验下的压缩指数C′c与一维固结下的Cc基本相等，且该结论与国内外其它地区软土在一维和等向固结试验下得到的结果一致[4,6,20]。

图4(b)给出了修正剑桥模型参数κ分别与一维和等向固结下的回弹指数Cs、C′s之间的关系。由图4(b)可知，κ与Cs之间存在较好线性关系，即

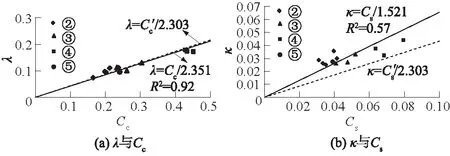
图4 上海软土修正剑桥模型参数λ、κ与一维固结下Cc、Cs之间的关系Fig.4 Relations between Cambridge model parameters λ and Cc, κ and Cs for Shanghai clay

κ=Cs/1.521 。

(4)

R2值为0.57，相比式(3)κ与Cs的相关性较差。因此，修正剑桥模型参数的κ值不能简单地用一维固结下的Cs估算，应该通过等向固结下的C′s进行计算，除了等向固结试验外，如何通过较为简单的方法估算C′s，后文将给出结论。

3 一维和等向固结试验结果与物理指标间的关系

根据前文所述，压缩指数与土的基本物理指标之间存在一定的相关性。本节分析了上海典型土层第②—第⑤层软土压缩指数Cc与wn、e0、wL和Ip之间的经验关系，并与一些已有的统计关系(表3)进行如图5所示的对比和分析。为了更加直观，表3中各关系式的序号与图5中的编号是相对应的。上文已经说明C′c与Cc基本相等，因此，关于等向固结下的C′c不做单独分析。

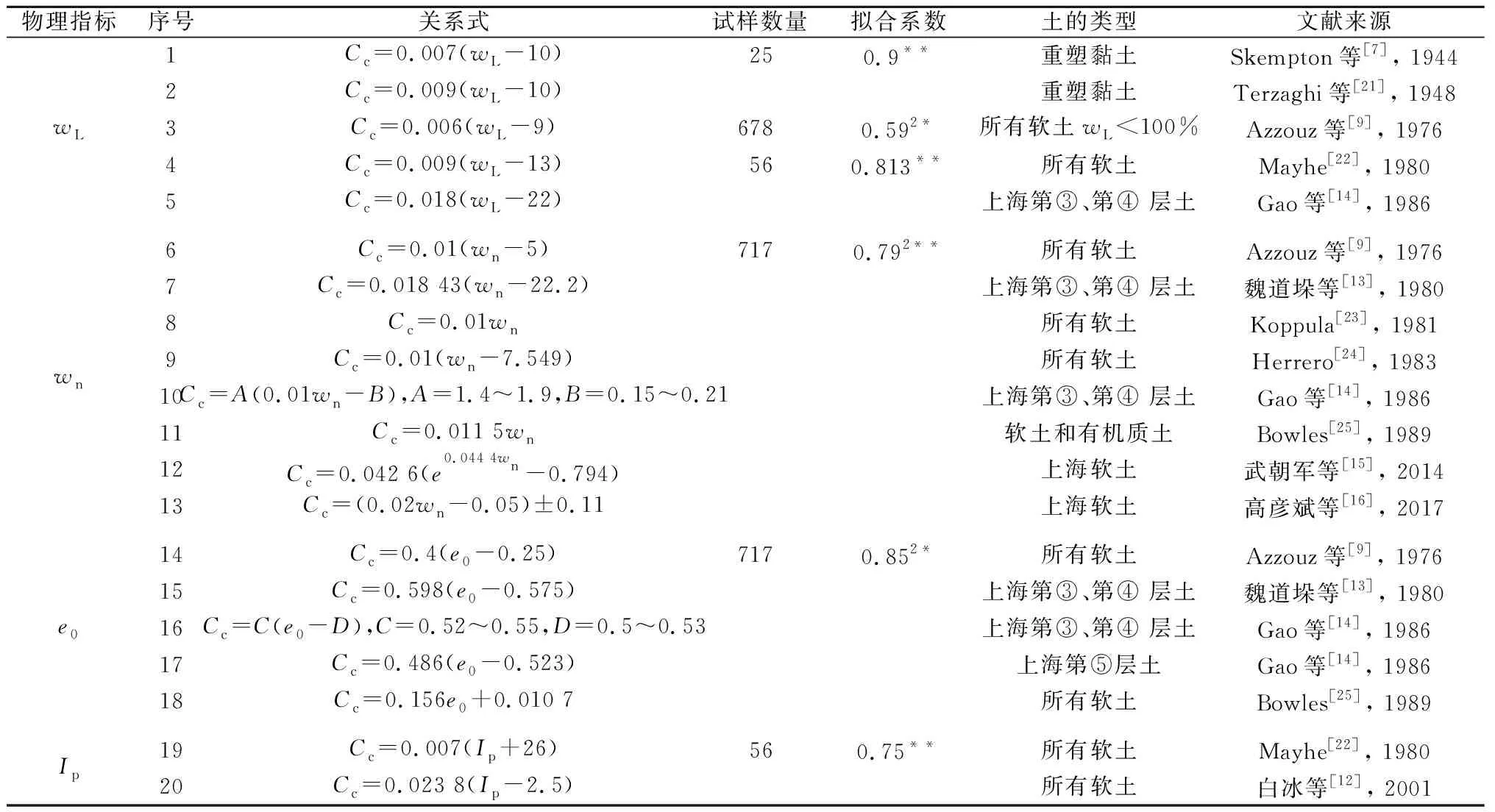
表3 软土压缩指数与对应物理指标的关系式Table 3 Empirical equations between compression index Cc and physical parameters of clay

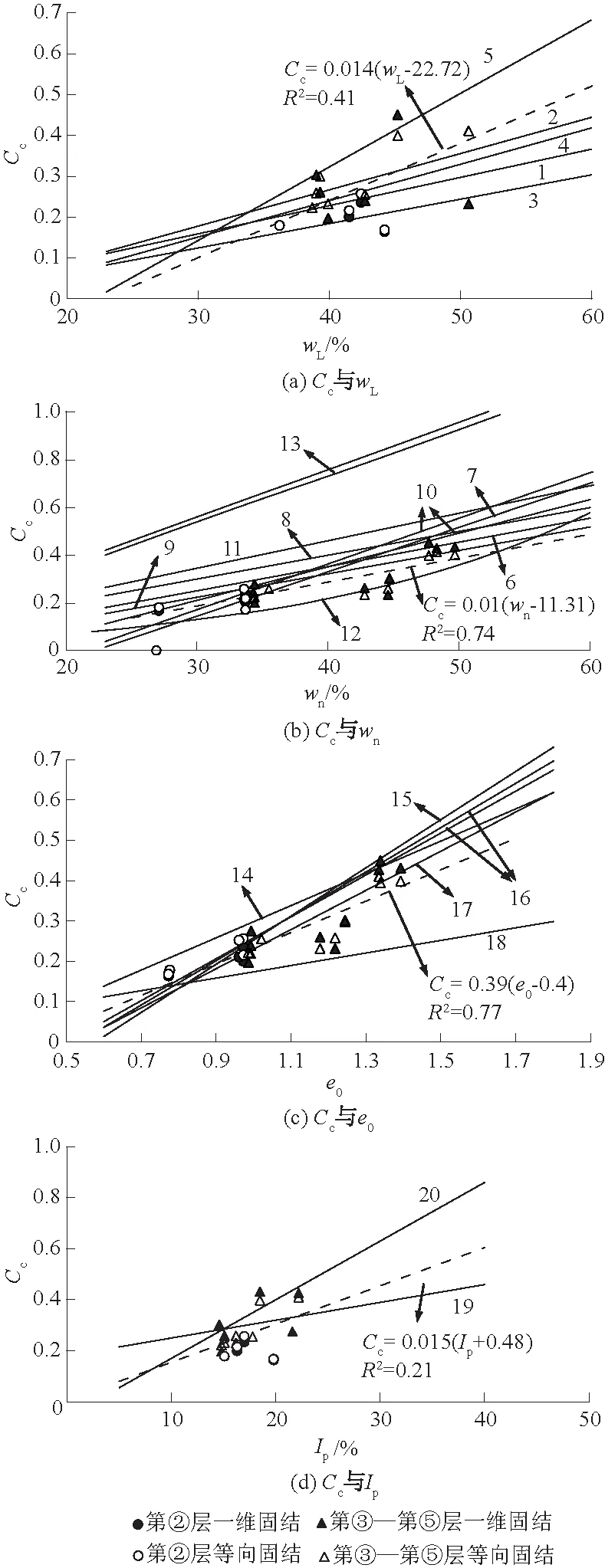
图5 压缩指数与物理指标之间的关系Fig.5 Relations of compression index against physical properties

从图5可以看出，Cc均随物理指标wL、wn、e0和Ip的增大而增大。如图5(a)和图5(d)可知，Cc与wL和Ip之间的相关性较差，决定系数分别为0.41与0.21；从图5(b)和图5(c)可以发现，Cc与wn和e0之间的相关性相对较好，决定系数分别为0.74和0.77，但不难发现试验结果与各个统计关系式之间还是较为分散。

由上文可知，Cc与基本物理指标之间经验关系的决定系数并不高。根据文献[26]发现日本典型原状土和重塑土的物理性质指标Cc/n0与Cc之间存在较好的线性关系，且其中土的物理指标与土层灵敏度无关。发现上海软土一维固结试验下的Cc/n0与Cc、Cs/n0与Cs之间均存在较好的线性关系(其中n0为初始孔隙率)，并给出相应的关系式[27]：

Cc/n0=0.014 3Cc+0.001 49 ,

(5)

Cs/n0=0.015 6Cs+0.000 141 。

(6)

式中n0=e0/(1+e0)，简化可得：

(7)

(8)

如图6所示，上海软土在一维和等向固结试验下Cc/n0与Cc、Cs/n0与Cs、C′c/n0与C′c、C′s/n0与C′s之间存在高度的线性关系。从图6(a)和图6(b)可知，上海第②—第⑤层软土一维固结试验下Cc/n0与Cc、Cs/n0与Cs之间的线性关系式与何平等[27]得到的式(5)和式(6)几乎重合，因此，上海地区第②—第⑤层软土一维固结试验下的Cc与Cs可根据式(7)与式(8)进行估算，但C′s的计算却不能简单地参考一维固结下Cs的计算方法进行确定。

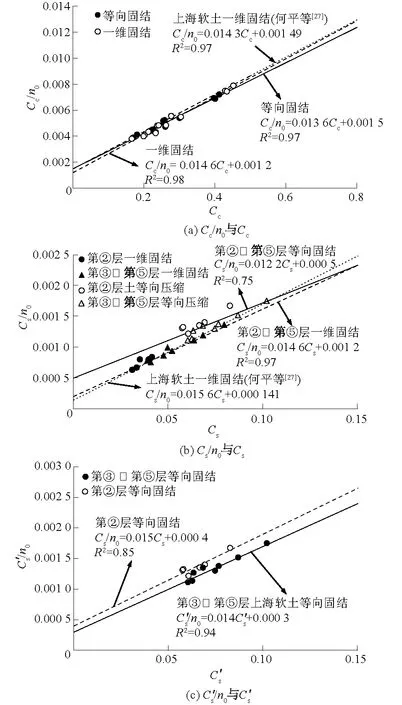
图6 上海软土Cc/n0与Cc、C′s/n0与C′s之间的关系Fig.6 Relations between Cc/n0 and Cc as well as C′s/n0 and C′s for Shanghai clay

为了能更简便地估算C′s，本文进行了进一步的分析，如图6(b)和图6(c)所示。从图6可以发现，等向固结下C′s/n0与C′s之间的离散性较大，而导致离散性较大的主要是第②层软土，前言部分已经介绍第②层软土属于超固结土。图6(c)给出了上海软土超固结土(第②层)和正常固结土(第③—第⑤层)软土等向固结下C′s/n0与C′s之间的关系，其线性决定系数分别为0.85和0.94，对比图6(b)中不考虑超固结特性时0.75的拟合系数，说明超固结特性对等向固结下回弹指数的影响较大。从图6(c)还可以看到，第②层超固结土层的数据点基本位于正常固结土C′s/n0与C′s拟合关系线的上方(图中虚线所示)，具体关系式如下。

第②层超固结土等向固结：

C′s/n0=0.015C′s+0.000 4 。

(9)

第③—第⑤层正常固结土等向固结：

C′s/n0=0.014C′s+0.000 3 。

(10)

由式(9)、式(10)进一步简化分别得到：

(11)

(12)

需要说明的是，n0最好<65%，否则离奇异点较近会引起负的压缩指数，上海地区典型土层对应的初始孔隙率n0一般不会超过60%。

4 中国沿海地区软土Cc与n0之间的关系

由于软土的压缩指数Cc/n0与Cc之间存在高度的线性关系，故针对图7所示的我国沿海地区海相沉积软土的Cc/n0与Cc之间的关系进行统计分析。除本文已有的上海地区软土的试验数据，还从十几篇文献中收集整理了中国沿海上海、福州[28]、深圳[29-32]、广州[20,33]、天津[34-38]、泉州[39]和温州[40-42]地区的121组具有代表性的软黏土的研究成果，且这些研究统计的数据点大多是通过几百组甚至近千组试样试验结果取平均值的方式得到的，比如温州(吴雪婷[41])的每组数据是分别通过312组试验结果取平均值得到，而泉州的每组数据则是分别通过对1 138个试样的试验结果取平均值得到的[39]。因此，统计结果具有较高的可靠性。文中涉及的这些地区基本涵盖了我国沿海的大部分地区，是一份较为详尽的统计资料。

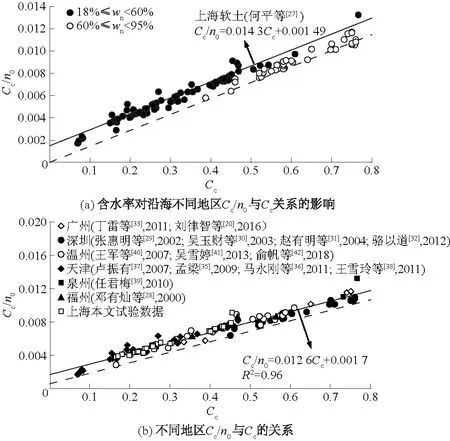
图7 我国沿海地区Cc/n0与Cc的关系Fig.7 Relationship between Cc/n0 and Cc in coastal areas of China

如图7(a)所示，按天然含水率取值大小排序后发现，含水率>60%的试验结果均位于何平等(2018)[27]给出的适用于上海软土的关系式(5)的直线下方，且有的数据点位于该关系式的奇点(n0=72%)处，因此，式(5)不适用于含水率>60%的其他沿海地区压缩指数的估算。如图7(b)所示，根据统计数据分析给出我国沿海大部分地区软土Cc计算的通用经验关系式，且这些地区Cc/n0与Cc关系呈高度的线性关系，决定系数高达0.96。由图7(b)中所有数据点下方的包络线(图中的虚线)不过原点可知，所有数据点均不在奇点处，因此，式(13)可用于中国沿海大部分地区软土压缩指数的估算，具体关系式为

Cc/n0=0.012 6Cc+0.001 7 。

(13)

简化得

Cc=n0/(588.24-7.41n0) 。

(14)

其中n0=e0/(1+e0)，n0最好<79%。

5 结 论

(1)通过对上海地区不同土层软土的一维和等向压缩回弹试验，得到不同土层在2种试验条件下的压缩指数与回弹指数。结果表明，实际应用修正剑桥模型参数λ的估算可参考一维固结下的Cc进行计算，因为2种试验条件下的压缩指数较为接近，但模型参数κ的计算则需要根据等向固结下的回弹指数C′s进行计算。

(2)对比当前研究给出的土体压缩指数Cc与其物理指标间的经验关系发现，虽然Cc与wn和e0间存在相对较好的相关关系，但离散性较大，而试验结果发现上海地区软土Cc/n0与Cc、C′s/n0与C′s之间存在较好的线性关系，决定系数R2分别达到0.97和0.94。同时发现等向压缩试验条件下得到的C′s值与土的超固结特性有关，并给出了超固结和正常固结两种情况下C′s的计算关系式，由此，上海地区软土变形指标可通过初始孔隙率进行估算。

(3)基于本文试验结果与搜集到的我国沿海其他地区试验数据，给出了能够适用于我国沿海地区(如上海广州、天津、深圳、温州、福州等)软土压缩指数与初始孔隙率之间的相关关系，且Cc/n0与Cc之间的线性决定系数R2值高达0.96。