基于月水量平衡模型的年径流模拟方法设计及应用
李 帅,杜 涛
(1.中国长江三峡集团有限公司,湖北 宜昌 443133; 2.长江水利委员会水文局,武汉 430010)
1 研究背景
河川长时段(月或年)径流量是流域水资源中长期规划及管理的关键指标[1]。因此,长时段径流量的准确模拟对于工农业长期规划、环境保护和水资源可持续利用显得十分重要[2]。目前,长时段径流量主要通过确定性水文模型[3]和随机模型[4]模拟得到。由于长时段水文过程已经概化掉存在于较短时段(时或日)水文过程中的随机不确定性因素,因此,长时段径流模拟遵循的原则是,在确保模拟精度的前提下,模型应尽可能简单稳健且参数较少[5- 6]。月水量平衡模型因其结构简单、物理意义明确、优选参数少,被广泛应用于水资源动态规划和管理[7],它以月降水量、月潜在蒸发量作为模型输入,结合流域中的土壤含水量,以质量守恒原理为理论基础,将各个水文过程或变量间的关系概化成经验公式,并通过该经验公式来模拟流域水文过程,最后以月径流作为模型输出[8]。
自20世纪40年代以来, 国内外学者为满足不同的研究需要, 相继提出了基于不同假设的月水量平衡模型, 如:TWBM[9](Thornthwaite Water Balance Model)、abcd[10]、VWBM[11](Vandewiele Water Balance Model)、TPWB[12](Two Parameters Water Balance Model)、MTPWB[13](Modified Two Parameters Water Balance Model)、DWBM[14](Danamic Water Balance Model)、RCCC-WBM[15](Research Center for Climate Change-Water Balance Model)等。这些模型结构简单,物理意义明确,曾被成功地应用于欧洲、美洲、澳洲以及亚洲的广大流域上,获得了满意的效果[16-20]。
作者也曾对比分析过8个国际上较为知名的月水量平衡模型的结构特点,并将其应用在中国南方50多个小流域的月径流模拟中,同样获得了满意的结果[8]。受此启发,本文首先将其中模拟效果较好的4种月水量平衡模型(即TWBM、abcd模型、VWBM和DWBM)应用在200个美国流域上,进一步检验其月径流模拟效果。然后,基于选定的月水量平衡模型的结构框架,设计一组年径流模拟方法,尝试通过改变模型输入的累积时长,对比分析不同模型基于不同累积时长输入的年径流模拟效果,以期为基于同一模型结构的不同时间尺度径流模拟提供一定参考。
2 月水量平衡模型介绍
水量平衡模型将流域不同水文过程描述为一连串水分储蓄和流动过程,主要包括实际蒸散发量、地下水补给量和径流量3部分。不同部分的物理机制解释和数学表示式不同,导致模型结构设计和复杂程度有所差异。本文选取的abcd模型、TWBM、VWBM、DWBM结构如图1所示。

图1 4种月水量平衡模型的结构示意图Fig.1 Structures of four monthly water balance models
月水量平衡模型结构的不同在于实际蒸发E和径流Q物理机制解释和数学形式表达[8],4个模型E和Q的计算公式如表1所示,图1和表1中涉及的变量符号及物理解释如表2所示。从图表中可以看出:①各模型处理E的方式不尽相同。除abcd模型将E处理为有效水量的非线性函数外,其他模型都将E处理为潜在蒸散发的函数,而VWBM和DWBM则进一步认为应同时考虑降水和流域前期蓄水量对E的贡献;② 4个模型均划分了直接径流和基流,区别在于abcd模型和VWBM的直接径流产生于有效水量经过土壤调蓄之后,而TWBM和DWBM则认为直接径流甚至在土壤没有饱和的时候就已经发生。

表1 4个模型实际蒸发量E和径流量Q计算公式Table 1 Formulas of E (actual evaporation) and Q (runoff) in four water balance models

表2 模型变量符号及物理解释Table 2 Variable symbols with physical explanations in four monthly water balance models
3 年径流模拟方法设计
本文基于月水量平衡模型的基本结构框架设计了一组共6种年径流模拟方法,分别记为ARS-1—ARS-6。其具体设计思路为:以L(L为12的约数,即L=1、2、3、4、6和12)个月的累积实测降水和潜在蒸发作为模型输入,通过模型模拟首先得到L个月的累积模拟径流,然后每12/L个等距离顺次分段相加得到模拟年径流量。由上述设计思路可知,ARS-1和ARS-3方法实际上是分别以实测月、季降水、潜在蒸散发作为模型输入,通过模型模拟首先得到月和季模拟径流,然后逐月和逐季累加得到模拟年径流;而ARS-6方法实质上是以实测年降水和潜在蒸散发作为模型输入,直接得到模拟年径流。
为了更加直观地体现这组年径流模拟方法的结构特征,以abcd模型结构为例,图2给出了基于abcd模型结构的年径流模拟方法的设计思路。从图2可以看出,本文设计的年径流模拟方法具有以下2个显著特点:

图2 基于abcd模型结构的年径流模拟方法设计思路Fig.2 Flowchart of annual streamflow simulation based on the structure of abcd model
(1)以月水量平衡模型结构为基本框架,在不增加额外参数的前提下,仅对月模型的输入和输出作时间聚集处理[21],最大程度保留了原模型的物理意义及径流模拟能力。
(2)以月模型为例子,提出了可变时间尺度的水文模拟方法,该方法不仅可以模拟年径流,还可以模拟季径流,方法简便、物理意义明确,为小时间尺度模型模拟长时间尺度径流提供了一个新的思路。
4 应用实例
4.1 资 料
本文以美国本土的200个MOPEX流域为研究对象,所用水文气象资料包括:1951—2000年的逐月降水量、潜在蒸散发量和径流量。MOPEX(Model Parameter Estimation Experiment)是模型参数估计实验的简称,它的主要目的是开发一种参数预估技术来实现水文模型和大气模型陆面过程的参数化策略[22]。MOPEX数据集不依赖于某一特定的模型,可以应用于绝大多数水文模型和陆面过程参数化方案的参数估计,并且范围和内容还在不断扩展和丰富[23]。MOPEX数据集向全球科研工作者开放,可以免费从MOPEX网站获取。世界各国科学家也可以向MOPEX提交满足标准的水文数据。MOPEX接收数据的标准非常严格,要求满足一定的空间和时间分辨率,并且经过整编。
美国本土面积广大,气候类型丰富多样,数据整编质量高。美国本土与中国纬度相近,有多种相似的气候类型,尤其是密西西比河流域与中国长江流域有很多共同点,可以为中国的水文研究提供参考[24]。
4.2 评价指标和优化算法
为了评价4种模型的整体表现,本文选用Nash-Sutcliffe效率系数NSE[25]、模拟总量相对误差RE[12]和Pearson相关系数CC[26]为精度指标对模型进行全面评价,它们的计算公式为:
(1)
(2)

SCE-UA算法是Duan等[27]于1992年提出的一种全局优化算法,由于SCE-UA算法简单,容易实现,一般能够很快达到全局最优,从提出至今在水文模型参数率定中得到广泛的应用和验证。SCE-UA算法的详细描述和计算步骤见文献[27]。
4.3 结果与讨论
为了全面检验abcd、TWBM、VWBM和DWBM 4种被选模型在美国本土流域水量平衡模拟中的效果,200个MOPEX流域近50 a(1951—2000年)的水文气象资料均被用来评价模型的总体表现。资料序列总长度的前2/3(1951—1983年)被用来率定模型参数,后1/3(1984—2000年)被用来检验模型。为了减小模型初始条件对模型模拟效果的影响,率定期的第1年被用来预热模型。
图3描绘了4种月水量平衡模型应用于200个MOPEX流域后的模拟精度(NSE、RE和CC)超过给定精度的流域比例。4种模型在200个流域上月径流模拟的平均表现如表3所示。从图3和表3可以看出,4种模型在MOPEX流域上均获得了较好的模拟效果,200个流域率定期和检验期的平均NSE均在0.7以上,平均CC均在0.85以上,且平均RE均在±0.05之间。其中,abcd模型的模拟效果最好,率定期和检验期的平均NSE分别为0.76和0.77,超过0.95的流域率定期和检验期的NSE>0.6;率定期和检验期的平均CC分别为0.87和0.89,超过0.95流域率定期和检验期的CC>0.7;率定期和检验期的平均RE均在±0.02之间,超过0.85流域率定期和检验期的RE落在±0.1之间。

表3 水量平衡模型月径流模拟平均表现Table 3 Means of evaluation indices of monthly streamflow simulation using the four water balance models in 200 MOPEX catchments in both calibration and validation periods

图3 4种模型月径流模拟精度≥给定精度的流域比例Fig.3 Percentage of catchments with values of the eval-uation indices (i.e., NSE, RE, and CC) calculated from 200 MOPEX catchments using 4 monthly water balance models greater than or equal to the values of given evaluation indices
表4给出了6种方法在200个流域上年径流模拟的平均表现。限于篇幅,图4仅描绘了基于4种月水量平衡模型结构框架的ARS-1年径流模拟方法在200个MOPEX流域上的模拟精度(NSE、RE和CC)超过给定精度的流域比例。

表4 基于4种月水量平衡模型的年径流模拟方法的平均表现Table 4 Means of evaluation indices of annual stream-flow simulation using the developed methods based on the structures of four water balance models in 200 MOPEX catchments in both calibration and validation

图4 ARS-1方法年径流模拟精度≥给定精度的流域比例Fig.4 Percentage of catchments with values of the eval-uation indices (i.e., NSE, RE, and CC) calculated from 200 MOPEX catchments using the ARS-1 method greater than or equal to the values of given evaluation indices
从图4和表4可以看出,随着模型输入累积时长的增加,年径流模拟方法在200个流域上的平均模拟精度整体表现出降低趋势,即ARS-1的整体表现优于其他5种。对于ARS-1而言,基于4种月水量平衡模型的年径流模拟方法在绝大多数流域上均获得了令人满意的模拟效果,200个流域率定期和检验期的平均NSE均在0.73以上,平均CC均在0.9以上,且平均RE均在±0.05之间。其中,基于abcd模型的年径流模拟方法模拟效果最好,率定期和检验期的平均NSE、CC和RE分别为0.9和0.84、0.95和0.95、0和-0.04。
为了测试不同月水量平衡模型在年径流模拟中的稳定性,图5给出了4种模型在200个流域上的年径流模拟平均精度(NSE和CC)与模型输入累积时长的关系。从图5可以看出,随着累积时长的增加,尽管4种模型的年径流模拟平均精度均表现出了一定的下降趋势,但DWBM下降速度最缓慢,表现最为稳定,其次是VWBM,再次是abcd模型,TWBM稳定性最差。
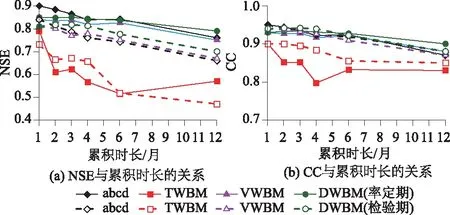
图5 基于4种模型的年径流模拟精度NSE和CC与模型输入累积时长的关系Fig.5 Relations of evaluation indices (i.e., (a) NSE and (b) CC) of annual streamflow simulation based on the structures of four models against accumulated time step L
5 结 论
(1)4个模型在200个MOPEX流域上的应用结果表明:无论是月径流还是年径流模拟,4个模型在绝大多数流域上均获得了令人满意的模拟效果,其中,abcd模型表现最优。
(2)随着累积时长的增加,4个模型年径流模拟精度均呈现出下降趋势,但DWBM的下降速度最缓慢,表现最为稳定。
(3)针对不同水文过程耦合存在的时间尺度匹配问题,基于月水量平衡模型的年径流模拟方法利用中小尺度上建立的水文模型进行尺度转换研究,为探讨较大尺度上的水文过程和规律提供了一种新思路。
(4)由于篇幅限制,本文仅采用了4种水量平衡模型和200个美国本土流域,未来可融入更多更新模型并应用到全球不同气候条件下的流域,进一步研究时间尺度与模拟精度的关系,对现阶段的结果进行验证。

