引江济淮凤凰颈泵站基坑降水方案优化

张国龙，范 越，张 伟，汪 啸，王金龙

(1. 安徽省水利水电勘测设计研究总院有限公司，合肥 230088；2.长江科学院 水利部岩土力学与工程重点实验室，武汉 430010)

1 研究背景

相较于传统的市政、建筑基坑，闸站基坑一般位于已有河道上，受季节和降雨影响，水位变动剧烈，对基坑施工影响较大。在闸站基坑施工过程中，为避免出现流土、管涌、坑底突涌等问题，需要进行基坑降水方案的优化研究。

优良的基坑降水方案应当是在保证基坑安全和地下水位降深满足要求的基础上，最大化施工便利程度，同时最小化基坑降水的总费用，包括降水井的建设费用和后期抽水的费用。数值模拟是基坑降水设计的常用方法，其基本流程是：根据场地的地质条件建立水文地质概念模型，在其基础上建立数学模型；结合地下水运动的初始条件和边界条件，对数学模型求解，可得地下水运移特征[1]；之后在模拟模型的基础上，调整降水井的布局和降水量，组成多个降水方案，并进行比对，得到基坑降水的优化方案。基于三维渗流模型进行基坑降水优化设计的研究有很多。张伟等[2]构建了江口水电站坝址区的三维渗流模型，论证了防渗帷幕和降水设计方案的渗控效果，采用有限元方法求解。骆祖江等[3]采用数值模拟方法，模拟了上海环球金融中心基坑场地多层含水层复合的地下水三维渗流场特征，以此确定基坑最优降水方案。陈华勇等[4]采用多目标模糊决策方法，对复杂地层与边界条件下的基坑降水方案作了优化设计。张伟等[5]通过一系列的降水试验，综合分析了基坑含水层渗透系数，并采用三维渗流模型复核验证了参数计算结果。Wang等[6]运用三维有限差分法对上海地铁9号线宜山路站深基坑降水进行数值模拟，结果显示止水帷幕和回灌的布置能减小基坑外地下水位的下降，有效地控制地面沉降。吴锐等[7]建立了三维渗流数值模型，将疏干井与减压井考虑在内，对基坑内承压含水层的降水效果进行模拟计算。王康达等[8]运用Modflow数值模拟软件研究了深基坑围护结构对减压井降水效果的影响。崔永高[9]模拟了基坑降水过程中不同工况下的渗流场，研究了在深厚强透水含水层中基坑降水的群井效应。游洋等[10]针对长江岸边某深大基坑降水方案进行了模拟计算，设计了2个降水方案，并进行了对比分析。

本文结合引江济淮重大工程，针对安徽芜湖凤凰颈泵站改造的基坑降水过程进行了优化研究，项目成果将为工程设计提供借鉴。该工程位于长江一级阶地上，地基呈典型的双层结构(二元结构)。上部由透水性弱的黏性土层组成，下部由透水性强的砂、砾、卵石层构成，且直接受江水充足地补给，进一步增加了基坑降水的难度[11-12]。

本文在前人研究基础上，综合运用“大井法”解析解和数值模拟2种方法计算了基坑涌水量，并将结果进行相互验证。基于构建的三维渗流数值模拟模型，对凤凰颈泵站改造工程基坑纯降水阶段的降水井数目、位置分布和井深进行优化研究，力求在满足基坑降水要求的前提下，减少基坑降水费用，降低基坑施工难度。通过对比多种方案的降水效果，总结了普遍性的降水井布置的经验和规律，对今后的闸站基坑降水具有一定的借鉴参考价值。

2 工程概况及水文地质条件

凤凰颈泵站位于安徽芜湖市无为县刘渡镇，是一座闸站结合、排灌结合的大型泵站，也是安徽省引江济淮的龙头工程。主要承担着巢湖流域防洪、排涝、农田灌溉、生态补水、水资源合理配置和高效利用、水环境改善等公益性任务。根据引江济淮工程设计要求，凤凰颈泵站需要进行改造重建，计划对原泵站前池底板进行拆除，将原泵房改造为重建泵站的进、出水通道及防洪闸。

本文针对工程第一阶段的基坑降水方案进行优化研究，在不建设防渗墙、仅依靠降水深井的条件下，要求将水位降至-6 m高程以下，以保证老站前池底板的顺利拆除。

工程区位于长江左岸，以河湖相冲积平原为主，主要地层分布见图1。根据勘探资料和室内试验成果资料分析，各土层主要参数建议值见表1。工程区地下水主要为孔隙承压水，水头受江河水位影响。地下水主要赋存于相对隔水层下部的②4层粉细砂、③层细砂和⑤2层中细砂夹砾石中。

表1 工程区各土层指标建议值Table 1 Suggested values of indices of soil strata in the project region

图1 引江济淮工程凤凰颈泵站FHP1-FHP1′地质剖面Fig.1 FHP1-FHP1’ geological profile of Fenghuangjing Pump Station of diversion project from the Yangtze River to Huaihe River

3 基于“大井法”解析解的基坑总流量估算

在进行三维渗流计算之前，本研究首先通过“大井法”解析解，初步计算了基坑降水的影响半径和涌水量。“大井法”是估算基坑降水流量的一种常用方法。把降水井群环绕下的基坑视作一个大的圆形的降水井，将地下含水系统概化为均质、各向同性且厚度均一的含水层。通过经验公式计算大降水井的井径和降水影响半径，将其代入相应的解析解计算公式，估算出基坑涌水量Q。大井法原理简单，计算便捷，在实际工程领域应用广泛[13-16]。

利用“大井法”计算基坑涌水量，首先要确定渗透系数K、大井井径r0和基坑降水影响半径R。工程区的主要含水层为：②4层粉细砂、③层细砂和⑤2层中细砂夹砾石层。根据等效渗透系数方法，工程区3层含水层的等效渗透系数由式(1)计算。

(1)

式中:Kp为等效渗透系数；Ki为第i层含水层的渗透系数；Mi为第i层含水层的厚度。计算得到本工程含水层的等效渗透系数为3.65 m/d，含水层深度为27.34 m。

工程区基坑形状近似为矩形，根据《管井技术规范》[17]中的式(2)估算基坑计算半径(大井井径)。

(2)

式中：η为形状系数；a和b分别为矩形的边长。

根据基坑设计图测量可得，基坑长和宽分别为152 m和126 m。基于基坑长和宽的取值，通过查表可知η取1.18。将上述值代入式(2)，计算得到基坑计算半径为82.01 m。

承压含水层的影响半径R为

(3)

式中:R为影响半径(m)；sw为降深(m)；K为渗透系数(m/d)。

初始水位取10 m，基坑水位降深需达到16 m，将水位降至-6 m高程。根据式(3)计算，降水影响半径为305.68 m。

结合工程实际条件，采用承压非完整井，半无限承压含水层的公式计算基坑降水预计的抽水量，即

式中：Q为基坑涌水量(m3/d)；M为含水层厚度(m)；r0为基坑计算半径(m)；l为过滤器工作部分的长度(m)。

工程区地表高程约10 m，上部主要含水层②4层的顶高程为-5 m。计算在不同降水井深度条件下，基坑水位降至-6 m的涌水量，计算结果见表2。

表2 不同降水井深度对应的基坑涌水量Table 2 Pumping volume of foundation pit corresponding to different dewatering well depths

从表2可以看出，在基坑降水深度一定时，降水井深度越大，相应的井管过滤器越长，基坑涌水量越大。根据计算结果，当井深为30～40 m时，基坑总涌水量在6 200～6 500 m3/d之间。

4 基于三维渗流模型的基坑降水方案优化

4.1 三维渗流模型的构建

图2 模型计算范围示意图Fig.2 Diagram of model computation range

模型四周边界均为给定水头边界。右侧边界BC给定为长江水位，并下切至-16 m高程，至③层细砂含水层。左侧边界，A点和D点为该处的地下水水位，取10 m，EF段水位取西河水位。长江和西河水位取枯水期10 a一遇水位，分别为9.85 m和8.55 m。根据钻孔情况，构建了工程区三维地质模型(见图3)，在此基础上构建了地下水数值模拟模型。其数学表达形式见式(5)。

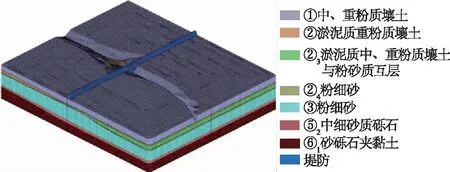
图3 工程区三维地质模型Fig.3 Three-dimensional geological model of the projectregion

式中:K为渗透系数(m/d)；H为地下水水位高度(m)；H(x,y,z)|Γ为三维流在边界Γ上点(x,y,z)处的水头值；φ1(x,y,z)为边界Γ上的已知函数。

采用GMS软件中的Modflow模块对三维渗流模型进行求解，共剖分14层，有效网格51.05万个。含水层渗透系数取值见表1。基坑范围与水位观测点位置见图4。

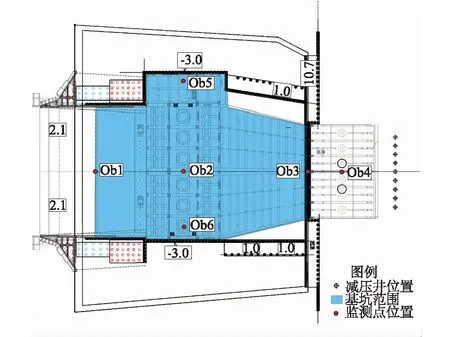
图4 基坑范围与水位观测点位置示意图Fig.4 Diagram of foundation pit scope and water level observation points

4.2 基坑降水方案优化研究

降水方案优化的主要目标有3个：①要保证基坑水位降至目标要求；②尽可能减少降水对基坑施工的干扰；③尽可能减少降水井数，降低总抽水量，以节约工程建设成本。

按照上述目标，首先复核了原设计降水方案(方案1)，共37口降水井，井深30 m，降水井布置见图5(a)。经计算，该方案可很好地满足降水要求，但方案布设的降水井数较多，有较大的优化余地。

其次，对降水井的空间布置进行了优化研究。在方案1的基础上，考虑抽水总量最小，将降水井集中布置在基坑内部，形成了方案2，共布置降水井30口，见图5(b)。经计算，该方案可以满足基坑水位降深要求。为了减小降水井布置对基坑施工的影响，考虑尽可能将降水井布置在基坑支护桩外侧，形成了方案3(见图5(c))。该方案将主要降水井均布置在基坑支护桩外，在基坑内布置补充降水井，以满足水位降深要求，共设降水井27口。经计算，该方案也可以很好地满足基坑各处的降深要求。该降水方案对施工影响小，需要布设的降水井数相对较少，各井抽水量分布相对均匀。因此，方案3可以作为候选方案之一。

最后，本次研究考虑了降水井的深度对降水效果的影响。将降水井深分别加至35 m和40 m，并对降水井的布置进行重新优化，形成方案4(见图5(d))和方案5(见图5(e))，研究井深变化对降水效果的影响。经计算，在井深35 m的条件下，仅需要基坑支护桩外围的18口降水井可以满足降深要求；在井深40 m的条件下，仅需要支护桩外围的12口井就可以满足水位降深要求。综合分析，方案4和方案5均可以作为候选降水方案。

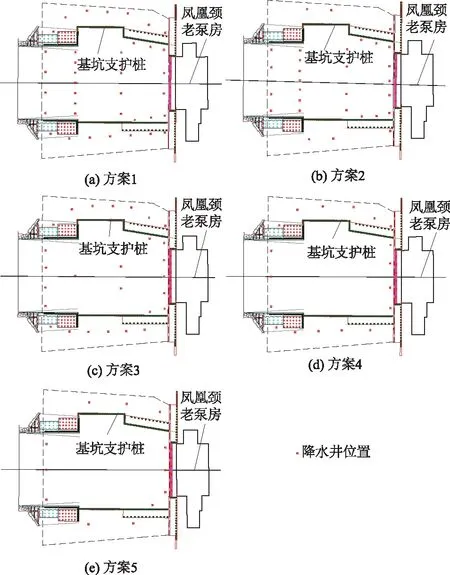
图5 方案1—方案5降水井布置示意图Fig.5 Layout of dewatering wells of scheme 1—scheme 5

各方案中观测点水位值和基坑涌水量的计算结果见表3。表3展示了各方案的统计指标。其中，单井抽水量极差为最大和最小单井抽水量的差值；单井抽水量相对极差为单井抽水量的极差与平均值的比值。在方案5条件下模拟得到的工程区平面及剖面水头值分布情况见图6(a)和图6(b)。方案5布设的降水井数量少，各井间抽水量分布更为均匀，利于水泵配购及降水过程控制，且降水井普遍布置在基坑支护桩外，利于基坑施工。综上，本次研究将方案5作为纯降水工况的推荐方案。

表3 降水方案计算结果综合对比Table 3 Comprehensive comparison of computation results of dewatering schemes

图6 方案5条件下在细砂层平面和基坑中心处剖面水头分布情况Fig.6 Water head distributions at the level of fine sand layer and the center of the foundation pit under the condition of Scheme 5

4.3 降水方案优化结果分析

4.3.1 基坑总涌水量计算结果分析

本次研究采用“大井法”解析解和三维渗流模拟2种方法计算了基坑总涌水量，表4统计了2种方法在不同井深条件下，基坑涌水量的计算结果。由表4可知，2种方法的计算结果相近，误差均在5%以内,甚至在井深为35 m和40 m的算例条件下，2种方法的计算结果误差<1%。2种方法相互验证，表明本次研究的计算结果可信度较高。

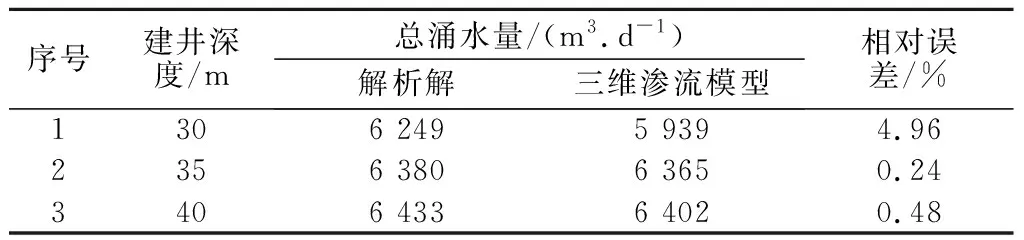
表4 2种方法计算结果对比Table 4 Comparison of computation results of the two methods

4.3.2 井深变化对降水井布置的影响

本节对比研究方案3—方案5这3个不同降水井深度的候选方案。在基坑范围内降深满足设计要求的前提下，分析降水井深度对布井数目、平均单井抽水量、基坑总涌水量等计算结果的影响。图7展示了降水井深度与布井数目、平均单井抽水量的关系。图8展示了降水井深度与基坑总涌水量的关系。

图7 降水井深与井数目、平均单井抽水量的关系Fig.7 Relations of dewatering well depth versus the number of wells and the average pumping volume of single well

图8 降水井深度与基坑涌水量的关系Fig.8 Relation of dewatering well depth versus total pumping volume of foundation pit

从图7可知，随着降水井深度的增加，需要布置的降水井数量逐渐减小，平均单井抽水量逐渐增加。降水井深度每增加5 m，平均单井抽水量增加约146 m3/d。而图8则表明，降水井深度越大，基坑总抽水量越大，但整体变化幅度不大。采用40 m的降水井比采用30 m的降水井，基坑总抽水量多463 m3/d，比采用35 m的降水井，基坑总抽水量多37 m3/d。

综合来看，当降水井深度增加，需要布置的降水井数目显著减少，单井出水量近似线性增加，基坑总涌水量变化幅度不大。因此，采用深度较大的降水井能在抽水费用基本不变的基础上，减少建井数目，节省工程成本。因此，建议采用深度为40 m的降水井。

4.3.3 布井均匀性和基坑总抽水量的关系探讨

本节综合对比了各降水方案，对布井均匀性和基坑总抽水量的关系进行了初步探讨。

由表3中的单井水量极差和相对极差这2项指标可以用来反映同一方案中，不同降水井之间的抽水量差异，从而量化布井均匀性。

结合各方案布井分布图可以看出，各降水井抽水量的差异越小，布井越均匀。在各方案中，方案5的单井抽水量相对极差最小，布井也更均匀一些。这表明，本次研究提出的推荐降水方案，能够将基坑内水位降至目标要求，同时兼顾布井的均匀性。

结合计算结果还可以分析布井均匀性和基坑总抽水量的关系。针对30 m井深条件下方案1—方案3，总抽水量最少的是方案2，最多的是方案3。结合图5(b)和图5(c)可以看出，方案2将更多降水井布置在基坑内部，因此井中水位降深能够有效影响到基坑内部，基坑总抽水量较少。反之，方案3将大量降水井布置在基坑外侧，这就使得降水井必须维持较大的水位降深，才能将基坑中心位置的地下水位降至目标要求，因此基坑总抽水量较大，带来了一定的抽水流量浪费。

因此，从减少基坑总抽水量的角度看，应将降水井主要布置在基坑内部；但另一方面，降水井设置在基坑内，会干扰基坑施工，并对工程安全造成不利影响。在实际工程中，应当综合考虑两项因素，选择合适的基坑降水方案。

5 结 论

本文基于“大井法”和三维渗流模型2种方法，对引江济淮凤凰颈泵站改造工程的基坑降水方案进行了优化研究，对比分析了降水井的空间布置和井深度变化对基坑降水效果的影响，并综合考虑了工程经济性和施工便捷性，提出了推荐降水方案。通过研究，本文得到了如下结论：

(1)采用“大井法”计算得到的基坑涌水量，与三维渗流模型计算得到的结果误差在5%以内。2种方法相互验证，表明计算结果可信度较高。

(2) 在基坑降水方案中，降水井空间分布越均匀，各井抽水量变化越小，更有利于抽水泵的配购。

(3) 在基坑降水满足降深要求的前提下，将降水井布置在基坑周边，对施工干扰较小，但会显著提高总抽水量。将降水井主要布置在基坑内部可以减少抽水总量，但同时会干扰基坑施工，并对工程安全造成不利影响。在实际工程中，应当综合考虑基桩内、外部布置两方面来设计基坑降水井的空间布局。

(4) 在基坑降水满足降深要求的前提下，降水井深度越大，总抽水量越大，需要布置的降水井数目越少。在实际工程中，应从含水层的条件、基坑降水工程的经济性、降水井深度与基坑总抽水量的相关关系等多个方面考虑，对降水井的优化方案进行决策。