垂直电场下扭转双层石墨烯光学吸收性质的理论研究*

周畅 龚蕊 冯小波2)3)†

1) (云南师范大学物理与电子信息学院,昆明 650500)

2) (云南师范大学,云南省光电信息技术重点实验室,昆明 650500)

3) (云南师范大学,可再生能源材料先进技术与制备教育部重点实验室,昆明 650500)

层间扭转角度是对石墨烯物理性质宽波段可调谐的一个新参量.本文采用2° ＜ θ ＜ 15°扭转角度下的连续近似模型,获得了不同扭转角度双层石墨烯分别在有、无电场下的能带结构,通过电子-光子相互作用跃迁速率,计算模拟了范霍夫奇点附近电子带内跃迁和带间跃迁所引起的光学吸收谱.结果表明,在无外加电场时,带间跃迁吸收峰的位置随着扭转角度的增大而发生从红外到可见光波段的蓝移,且吸收系数增大,带内跃迁的光学吸收系数相对于带间跃迁高出2 个数量级;而存在外加电场时,两个范霍夫奇点在波矢空间的位置发生偏移,带间跃迁吸收峰发生分裂,且两个分裂的吸收峰位置随着电场强度的不断增大而反向行进.上述研究结果对石墨烯材料在光电器件方面的应用有一定指导作用.

1 引言

石墨烯是由碳原子组成的二维蜂窝状层状结构材料,因其具有高的载流子迁移率、较强的电导率、高的透光性等优异的光电特性受到科学家的广泛关注[1-6].随着现代纳米合成技术的发展和化学加工工艺的不断丰富,可以控制石墨烯原子层间发生一定角度的扭转,构成扭转石墨烯材料[7].当层间扭转一定的角度时,会改变原有石墨烯晶格的周期性和对称性,晶格结构出现Moiré图案[8];层间周期性势场得到调制,从而改变了载流子能态,费米面附近的电子能态密度出现范霍夫奇点(van Hove singularities,VHS)[9,10];原有能带可能发生杂化而形成平带[11].因而在扭转石墨烯材料中会出现霍夫斯坦德蝴蝶、超导、量子化反常霍尔态等各种新奇的物理现象[12-15].扭转石墨烯体系的物理性质成为当前科学研究的前沿与热点问题之一.

扭转角度是对石墨烯光学性质宽波段可调谐的又一个新的参量.非扭转石墨烯材料由于其中心对称性原本不具有偶数阶非线性光学效应,但2020 年美国加州大学伯克利分校Yao 课题组[16]发现当扭转角度θ=6°时,扭转双层石墨烯(twisted bilayer graphene,tBLG)的非线性光学极化率可以达到2.8 × 105pm2/V,其数值已经可以和单层MoS2等具有很强光学非线性的材料相比拟;Xia 课题组[17]研究了小角度tBLG 在5—12 μm 波段的光学响应,发现当θ=1.81°时,光学响应可以达到26 mA/W;北京大学刘忠范研究组[18]测量了tBLG 与等离子体集成器件中的光电流,发现可以通过调节扭转角度达到跃迁共振,从而使光电流增强80 倍;韩国Yeom 研究组[19]测量了tBLG 材料中三次谐波效应的非线性光学极化率,发现比在单层石墨烯中增强了60 倍,并且利用调节扭转角度使三阶非线性光学效应得到增强.理论方面,Yu 等[20],Moon 和Koshino[21],Moon 等[22],Tabert 和Nicol[23],以及Stauber 等[24]分别采用第一性原理、连续近似模型或者紧束缚方法对tBLG 的能带结构以及光电导、光吸收等性质进行了理论研究,去探究扭转角度对石墨烯光学性质宽波段可调谐的物理机理.

从目前的研究结果来看,tBLG 是很好的光学材料,而光学吸收则是将其运用于光电器件的有效途径之一.外加电场是将石墨烯等光学材料应用于光电器件时对其性能调谐的有效手段.文献中已有报道,通过在双层非扭转石墨烯层间外加垂直电场,由于上下两个石墨烯层间电势不对称导致费米面附近抛物线型能带的带隙打开,且此带隙的大小受电场强度的控制[25-27],通过调节电场从而去调制光谱[28].对于扭转双层石墨烯,Yu 等[20]探测了tBLG 在不同栅电压控制下的光电导率,发现由于层间电位不对称破坏了原来的能带结构,共振峰的强度和能量随栅压发生变化.考虑到目前对于外加电场下tBLG 光学吸收理论研究的不足,为进一步从理论上弄清外电场结合扭转角度对双层石墨烯光学性质的调制机理,本文以tBLG 为研究对象,选取扭转角度范围2° ＜θ＜ 15°,采用连续近似模型计算了其分别在有、无外加垂直电场时VHS 附近发生光学跃迁的吸收系数,得到了不同扭转角度和外电场强度下的光学吸收谱,研究了扭转角度和外加电场对光学吸收性质的调制规律.研究结果表明,通过改变扭转角度可以实现对tBLG 的载流子带间跃迁光学吸收从可见光到红外宽波段的调谐,扭转角度增大,吸收峰发生蓝移,吸收系数增大.若外加垂直匀强电场,会使双层扭转石墨烯能带结构的对称性发生改变,从而导致可见光到近红外波段带间跃迁吸收峰发生分裂,且两个分裂峰间距随外加电场增大而增大,出现两个吸收峰随外加电场的增大而反向行进的现象.扭转双层石墨烯在外电场下的此项特性可以运用于制作可调谐双波段滤波器.

2 理论模型与计算

考虑AB 堆积的双层石墨烯层间发生θ角度的扭转,构成了tBLG.其晶格结构在某些特定的扭转角度下会呈现出具有周期性的Moiré花纹,如图1(a)所示.扭转也引起两个石墨烯原子层间发生一定程度的解耦,使得两个原子层各自的第一布里渊区发生相对分离,形成两个狄拉克点K和Kθ,如图1(b)所示.两个狄拉克点之间偏移量ΔK=KKθ,且与扭转角度相关[29,30],ΔK ∝sin(θ/2).当扭转角度θ较小时(2° ＜θ＜ 15°),晶格形成超胞的周期远远大于原子尺度,也远远大于非扭转体系的晶格周期,因而可以采用连续近似模型来研究其电子能态.早在2007 年Santos 等[31]就采用该模型成功描述了tBLG 费米面附近的电子能态.在无外加电场情况下,扭转双层石墨烯的有效哈密顿量可以描述为

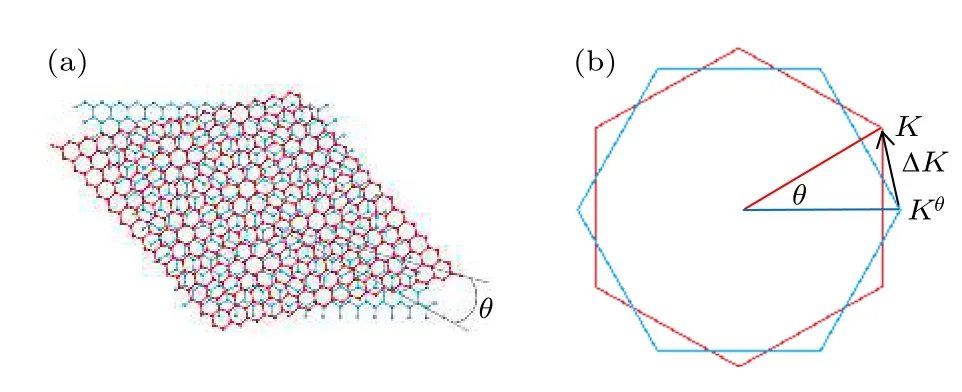
图1 (a) tBLG 的原子结构图,θ 为层间扭转角度;(b) tBLG的第一布里渊区,K 和 Kθ 为来自于上下两个单层石墨烯的狄拉克点Fig.1.(a) Atomic structure for tBLG,θ is the twist angle between layers;(b) the first Brillouin region of tBLG,where K and Kθ are the Dirac points of the upper and lower monolayers.

其中An和Bn表示第n层对应单胞中的两种不同的原子,r是单胞对应的位置矢量,0,G1和G1+G2是扭转形成的晶格超胞对应的倒格矢量,且其傅里叶分量为

其中φ=2π/3[33];是层间跃迁参数,它反映着扭转层之间的耦合强度,取值100 —150 meV[34].

当tBLG 上垂直施加一个匀强电场时,相邻两个石墨烯原子层之间会有一个电势差,它受到外加电场强度的调控[35].此时引入变量U表示层间能量差,得到外加垂直电场下的扭转双层石墨烯的有效哈密顿量如下:

基于上述得到的有效哈密顿量,通过将其对角化可以计算出扭转双层石墨烯的能带结构和电子能态.在计算中,层间跃迁项Htwist的傅里叶分量被统一简化为,这个简化的模型被证实仍然保持了原来哈密顿量的拓扑普适性和波函数的手性,且已在理论计算中被广泛采用[23,32].当频率为ω的光波照射到材料上,材料发生光吸收,低能态的电子吸收一个光子能量ℏω跃迁到高能态.单光子跃迁速率为

式中φi和φf分别表示电子跃迁过程中的初态及末态;Ei和Ef为对应的能量.根据经典电动力学,电子在光场中的正则动量为其中A=Ae是光矢量势,A是光矢量势的大小,e=(ex,ey)是矢量势方向的单位矢量.电子在光场中总的哈密顿量H可以表示为

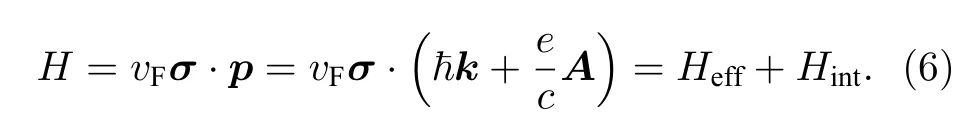
因而,光子与电子相互作用的哈密顿量Hint=(evF/c)A·σ,vF=106m/s 是费米速度,σ为泡利矩阵.材料的光学吸收系数与载流子跃迁速率有如下关系式:

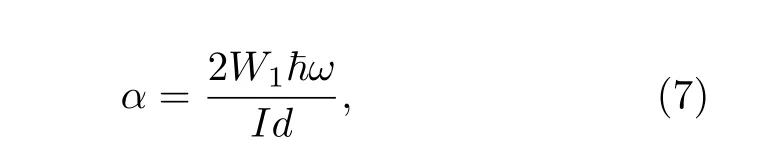
式中,d=0.335 nm 表示两个石墨烯原子层的间距,本文不考虑石墨烯由于层间扭转所导致原子层的褶皱,而认为每个原子层是一个二维平面.入射光强度,εω为光频介电常数.

3 计算结果与分析

为满足连续性近似模型的适用条件,选取了2° ＜θ＜ 15°范围内能够形成Moiré图案的几个扭转角度,通过将哈密顿矩阵中的波矢离散化以及哈密顿矩阵对角化,分别计算和模拟了tBLG 有无外电场时的能带结构以及相应的带内跃迁、带间跃迁光学吸收谱.这里要特别说明的是,对于极小的扭转角度θ＜ 2°,一方面考虑到层间杂化能对费米速度的影响,尤其是当扭转角为某几个特定值的时候(称之为“魔角”,例如θ≈ 1.05°[11,36]),费米速度为0,出现“平带”;另一方面,在扭转角度极小时,通过计算电子态密度发现晶格中处于AA 堆积区域的原子存在着局域化的电子态[37],而连续近似模型并不能够很好地描述这种局域化的状态,因此本连续近似模型不适用极小扭转角度(θ＜ 2°)的情形[38].至于稍大的扭转角15° ＜θ＜ 30°,tBLG的上下两个石墨烯层之间基本发生解耦,形成两个孤立的石墨烯单层[39],其费米速度近似等于单层石墨烯的费米速度,此时更加适用于Mele 模型[40].因而在连续近似模型下,无外场作用时,扭转3.89°的双层石墨烯能带结构如图2 所示,此时能带结构与无扭转时的零带隙双抛物线型结构有很大不同[41],两个分开的狄拉克锥在鞍点附近互相交叠发生能带杂化,形成了两个高能态密度的范霍夫奇点VHS1和VHS2,进而导致在鞍点附近电子能态有别于零带隙的狄拉克点K和K θ.

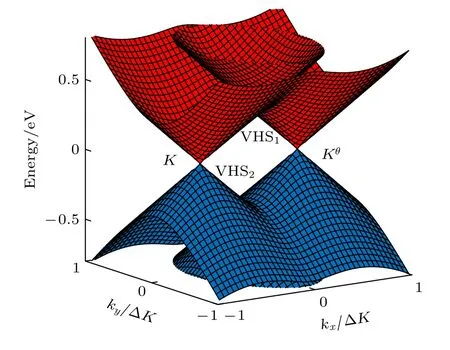
图2 无外电场时θ=3.89°的tBLG 三维能带结构图.K和K θ 为两个狄拉克点,VHS1 和VHS2 为两个范霍夫奇点Fig.2.The 3D band structure of tBLG at θ=3.89°without external electric field.K and K θ are two separate Dirac points,VHS1 and VHS2 are two van Hove singularities.

双层石墨烯层间扭转不同的角度对应的能带结构有所不同,如图3 所示.扭转角度发生改变时,两个范霍夫奇点均在同一个波矢点,不会因为扭转角度发生改变而改变,但两个范霍夫奇点之间带隙ΔEVHS随着扭转角度的增大而增大.范霍夫奇点源于两个分开的狄拉克点K和Kθ在其中点附近区域的杂化,当发生层间扭转时,狄拉克点附近的费米速度发生了重整[31],重整化的费米速度随着角度增大而增大,两个狄拉克锥对应的费米速度的增大使得在中点处杂化的能级位置逐渐远离费米面,所以两个范霍夫奇点之间带隙ΔEVHS被拉大,此时而在小角度近似下,vFℏΔK∝θ,即ΔEVHS与θ成正比[9].BE1和BE2表示距离VHS 最近另一个导带或者价带的带边.箭头显示了范霍夫奇点附近所有可能的光学吸收跃迁过程,包含了带间跃迁和带内跃迁两种形式,当初、末态能量之差Ef—Ei=ℏω时达到共振.值得注意的是,这里只计入了电子在非对称能带之间的跃迁(VHS2到BE1,BE2到VHS1),而对称能带之间(VHS1到VHS2,BE1到 BE2)不会发生跃迁,这已经被相关文献所证实[21].当扭转角度增大时,虽然两个范霍夫奇点之间的带隙ΔEVHS增大,但导带内或者价带内的VHS 和 BE 之间的能级间距数值几乎保持不变.VHS 和 BE 之间的能级间距与层间跃迁项有关,在本文中,取=110 meV[11].

图3 无外电场时四个扭转角度下tBLG 的能带结构图 (a) θ=3.89°;(b) θ=5.09°;(c) θ=7.34°;(d) θ=9.43°.其中红色(蓝色)箭头表示可能发生的带间(带内)跃迁,蓝色虚线为费米面Fig.3.The energy band structure of TBG at four twisted angles without electric field:(a) θ=3.89°;(b) θ=5.09°;(c) θ=7.34°;(d) θ=9.43°.Red (blue) arrow is the possible interband (intraband) transitions,and the dashed blue line shows the Fermi level.

考虑范霍夫奇点附近的光学吸收跃迁,分别画出了五个不同扭转角度下双层石墨烯发生带间跃迁和带内跃迁引起的光学吸收谱,如图4 所示.所有吸收谱均只有一个共振吸收峰.带间跃迁引起的吸收峰位于可见光到近红外波段,而带内跃迁引起的吸收峰则位于远红外波段(约11300 nm).对于带间跃迁,吸收峰的位置随着扭转角度的增大发生蓝移(从近红外波段蓝移到可见光波段),而带内跃迁吸收峰的位置并没有受到角度的影响.基于之前的能带结构随扭转角度的变化情况,非对称的带间跃迁仅当入射光子能量大于ΔEVHS时,电子才会从低能量的VHS2跃迁至BE1或者低能量的BE2跃迁至VHS2,进而产生共振跃迁吸收;ΔEVHS随着角度增大而增大,这导致了带间跃迁达到共振时所需入射光子能量变大,对应的峰值随之蓝移.实际上,范霍夫奇点的位置对应了电子能态密度(density of states,DOS)谱中在费米面附近能态密度峰所处的位置,两个对称范霍夫奇点的能量间隔相较于单层石墨烯范霍夫奇点的能量间隔更小,因此更容易发生载流子光学吸收跃迁,并且其能带间隔会随扭转角度的增大而增大,从而导致吸收峰发生蓝移[9].与带间跃迁不同的是,对于带内跃迁,在小角度范围内导带或价带内VHS 与BE 之间的能级间距几乎保持不变,故电子发生带内跃迁需要的入射光子能量不会随扭转角度改变.此外,不论是哪种跃迁模式,共振峰的数值都随着扭转角的增大而变大,这是因为吸收系数α与入射光子能量 ℏω成正比,所需要的入射光子能量随扭转角度增大,导致了吸收系数α的增大.从计算结果来看,带内跃迁引起的光学吸收系数比带间跃迁高了差不多2 个数量级.

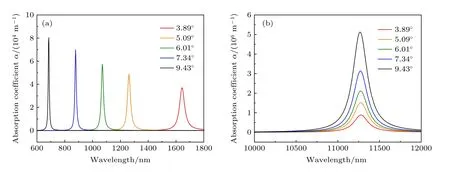
图4 不同扭转角度下tBLG 在范霍夫奇点附近的光学吸收谱 (a) 带间跃迁光学吸收谱;(b) 带内跃迁光学吸收谱Fig.4.Optical spectrums for tBLG around VHS with 5 different twisted angles:(a) Optical spectrums for interband transitions;(b) optical spectrums for intraband transitions.

若将tBLG 置于不同强度的垂直匀强电场中,其能带结构如图5 所示.通过对比可以发现,当施加垂直电场后,两个狄拉克点K和Kθ(kx/ΔK=±0.5)相对于费米面εF分别向上或向下移动,因而两个范霍夫奇点的位置不再在同一个波矢点,与两个带边顶点BE1和BE2一起往左或右偏移至k1和k2两点,使原来能带结构在波矢空间的轴对称性被破坏.综合图3 和图5,说明扭转角度只是改变了两个范霍夫奇点之间的能量差,不会改变其位置;而外加电场则会改变两个范霍夫奇点在波矢空间的位置,同时会改变相应跃迁能级差,具体数值见表1.在电场强度一定时,若改变石墨烯层间扭转角度,得到的光学吸收谱随扭转角度的变化规律与无电场时情况相似,且与Yu 团队[19]的研究结果吻合.

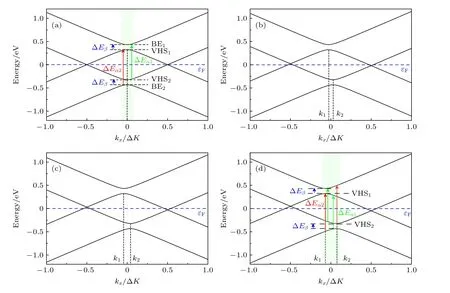
图5 不同外加电场下tBLG 的能带结构图(θ=3.89°) (a) U=0 meV;(b) U=40 meV;(c) U=60 meV;(d) U=100 meV.其中箭头表示可能发生的带间或者带内跃迁,蓝色虚线为费米面,黑色虚线表示范霍夫奇点的位置Fig.5.The energy band structure of tBLG at θ=3.89° with or without electric field:(a) U=0 meV;(b) U=40 meV (c) U=60 meV;(d) U=100 meV.The arrows are the possible interband (intraband) transitions,and the dashed blue line shows the Fermi level,and the dashed black lines are the positions of VHS.

表1 不同电场强度下tBLG 能带结构几个关键点的位置及带间能级差(θ=3.89°)Table 1.Positions of key points and energy level differences (θ=3.89°) in the band structure of tBLG under different electric field intensities.

为了探索外加电场强度对扭转双层石墨烯光学吸收的调制作用,描绘了层间分别扭转3.89°,6.01°和9.43°时双层石墨烯在不同外加电场强度下的光学吸收谱,如图6 所示.对于不同的层间扭转角度,其显著共同特性表现在以下两方面.1) 对于带间跃迁吸收谱,随着电场强度的增加,原本无电场时的单个光学吸收峰影响逐渐分裂为两个峰,并且这两个峰之间的间距会随着层间能差增大而逐渐拉大.这正是由于外加电场所引起能带结构对称性的破坏,两个范霍夫奇点处非对称能带间的能量差(ΔEα1和ΔEα2)一个减小,一个增大,导致了对应的吸收峰一个发生红移,一个发生蓝移,从而出现吸收峰发生分裂并随着电场强度的增大而反向行进.这个有趣的现象可以将双层扭转石墨烯用于可调谐双波段光波过滤器中.2) 范霍夫奇点处的带内跃迁所引起的光学吸收其吸收峰的位置和数值几乎不受外加电场的影响.通过表1 可知,外加电场的变化虽然可以改变范霍夫奇点的位置及其相应的能级差,但并不会大幅改变导带或价带内相应位置(VHS1到BE1,BE2到VHS2)的能量差ΔEβ.

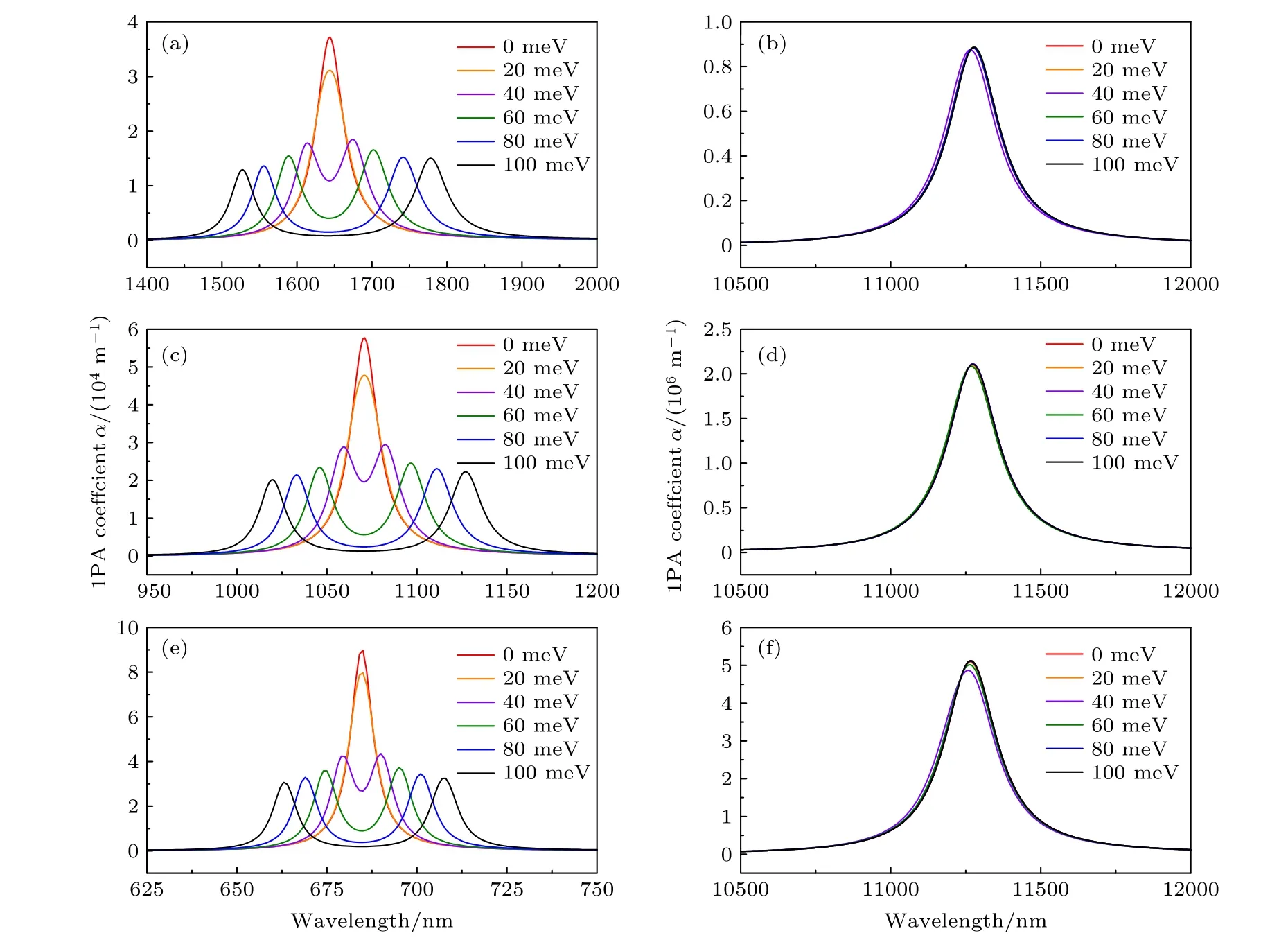
图6 不同电场强度下tBLG 范霍夫奇点附近的光学吸收谱,三种扭转角度下的带间跃迁吸收谱(左列)和带内跃迁吸收谱(右列) (a),(b) θ=3.89°;(c),(d) θ=6.01°;(e),(f) θ=9.43°Fig.6.Optical spectra for tBLG around VHS with different perpendicular electric field intensities,and optical spectra for interband transitions (left column) and Optical spectrums for intraband transitions (right column) under three twist angles:(a),(b) θ=3.89°;(c),(d) θ=6.01°;(e),(f) θ=9.43°.

4 结论

本文基于2° ＜θ＜ 15°扭转角度下的有效连续近似模型分别描述了有、无外电场作用下扭转双层石墨烯的能带结构,利用有效哈密顿量对角化后得到的本征值和本征函数进行了光学吸收系数的数值计算,得到了范霍夫奇点附近导带和价带的带内跃迁及带间跃迁所引起的光学吸收谱,分析了扭转角度以及外加电场强度对光学吸收的影响.研究发现:带间跃迁引起的光学吸收发生在可见光至近红外波段,带内跃迁引起的光学吸收发生在远红外波段,带内跃迁光学吸收系数比带间跃迁光学系数高差不多2 个数量级.无电场时,增大扭转角度不会改变两个范霍夫奇点的波矢位置但会带来该处的能级差增大,从而导致带间跃迁光学吸收峰发生蓝移;而带内跃迁的共振峰的位置几乎不受扭转角度的影响.外加电场时,会带来两个狄拉克锥的上下移动,从而导致范霍夫奇点左右移动,破坏了双层石墨烯能带结构原本的对称性.两个范霍夫奇点处的带间跃迁能级间隔一个变大一个变小,从而导致带间跃迁吸收峰发生分裂,并随着外加电场的增大而分别发生蓝移和红移,因而两个吸收峰间隔随外加电场强度的增大而增大;而带内跃迁吸收峰的位置和大小却完全不受外加电场的影响.本文理论计算结果可为进一步将扭转石墨烯应用于可调谐双波段滤波器等光电器件提供理论指导.