N 型局部有源忆阻器的神经形态行为*
王世场 卢振洲 梁燕 王光义
(杭州电子科技大学电子信息学院,杭州 310018)
局部有源忆阻器(locally-active memristor,LAM)凭借其高集成度、低功耗和局部有源特性等优点,在神经形态计算领域显示出巨大的潜力.本文提出了一种简单的N 型LAM 数学模型,通过揭示其非线性动力特性,设计了N 型LAM 神经元电路.采用Hopf 分岔、数值分析等方法定量研究了该电路的动力学行为,成功模拟了多种神经形态行为,包括全或无行为、尖峰、簇发、周期振荡等.并利用该神经元电路结构模拟了生物触觉神经元的频率特性.仿真结果表明:当输入信号幅值低于阈值时,神经元电路输出信号的振荡频率与输入信号强度呈正相关(即兴奋状态),并在阈值处达到最大值.随后,继续增大激励强度,振荡频率则逐渐降低(即保护性抑制状态).最后,设计了N 型LAM 硬件仿真器,并完成了人工神经元电路的硬件实现,实验结果与仿真结果、理论分析相一致,验证了该N 型LAM 具备的神经形态行为.
1 引言
随着大数据时代的到来,对计算系统的计算速度、集成度和能耗的要求也越来越高.面临这些挑战,传统基于冯诺依曼架构的计算结构逐渐难以应对[1,2].而神经形态计算因其高节能效率和大计算容量,显示出巨大的应用潜力.
近年来已经使用各种技术探索神经形态架构,如CMOS[3]、自旋电子[4]、忆阻器[5]等.其中,基于脉冲神经网络(spiking neural networks,SNNs)的神经形态计算架构能通过时间编码,获得更多的信息和更强的计算能力,因而被认为是强有力的候选者[6-8].目前已有将CMOS、忆阻器等技术应用至SNNs 的硬件电路搭建[7-13].MOS 管由于其物理限制和动力特性的缺乏,仅构建神经元电路就需要数十个器件.因此,构建复杂的神经网络,CMOS的体积和功耗限制了其发展和应用.文献[7,14]使用数十亿个晶体管构建一种非冯诺依曼架构,实现神经网络的应用.局部有源忆阻器(locallyactive memristor,LAM)具有高集成度、低功耗和局部有源特性等优点[15-23],使用较少器件就能实现人工神经元.文献[5]指出一个三阶Mott 忆阻器可实现多种神经形态行为,为忆阻器在神经形态计算领域奠定了基础.
忆阻器在神经形态计算中主要用于模拟突触和神经元.忆阻器渐变可调的阻态可模拟神经突触的可塑性.文献[24,25]利用忆阻器交叉阵列来存储神经网络的突触权重.文献[26]利用忆阻器作为电子突触,模拟出生物大脑内的放电时间依赖可塑性.
Chua 等[27,28]曾指出,复杂的神经形态行为存在于局部有源区域.因此,利用LAM 的非线性和局部有源特性,可以设计神经元电路,将其应用至神经网络.LAM 在其直流电压-电流(DC voltagecurrent,DCV-I)特性中具有负微分电阻(negative differential resistance,NDR)或电导区域,可分为S 型(电流控制)与N 型(电压控制).目前基于忆阻器的人工突触和尖峰神经元正被广泛研究以构建SNNs 的硬件实现.文献[29]使用忆阻器神经元和1T1R 忆阻器突触阵列整合SNNs,实现忆阻器突触阵列的权重到神经元振荡频率的转换.文献[30]提出并实验验证了基于NbOx忆阻器的尖峰神经元电路.文献[31]利用TiO2忆阻器开关特性来实现神经元电路.文献[32]首次提出并实验证明了一种基于NbOxMott 忆阻器的人工尖锋传入神经.然而,以上所有忆阻器件都是S 型LAM,目前N 型LAM 在神经形态计算中的应用报道较少.为此,本文将提出一种简单的N 型LAM 数学模型并展现了它的电学特性,设计基于N 型LAM 的神经元电路,定量研究了电路的动态特性,模拟了人工神经元的神经形态行为,数值分析其频率特性;给出了N 型LAM 的硬件仿真器以及设计的人工神经元电路的硬件实现及实验结果.
2 N 型LAM 数学模型及特性分析
根据蔡氏展开定理[33],一个通用电压控制型忆阻器可以表述为

其中i和v表示流经忆阻器的电流和忆阻器两端的电压;GM(x)为忆导函数;f(x,v)是关于忆阻器状态变量x和电压v的函数.基于 (1) 式,本文提出了一种简单的N 型LAM 数学模型,其表达式为

其中τ=10—5,α=9,d1=10—4,d0=2.4 × 10—3.
对上述N 型LAM 施加正弦信号v(t)=5 sin(2πft),得到该忆阻器的电压-电流特性曲线,如图1 所示.其中黑色、红色、蓝色曲线分别对应激励信号频率为10 kHz,50 kHz 和1 MHz.观察图1 可以发现,当激励信号是偏置为零的正弦信号时,该N 型LAM 展现出忆阻器特有的捏滞回环曲线,且曲线闭合面积随着频率的增大逐渐减小.

图1 N 型LAM 不同频率下的捏滞回环曲线Fig.1.Pinch hysteresis loop curves of the N-type LAM under different frequencies.
DCV-I特性对LAM 的动力学行为具有重要的意义.为得到该忆阻器的DCV-I特性,使输入电压v=V,即 (2)式可以转化为
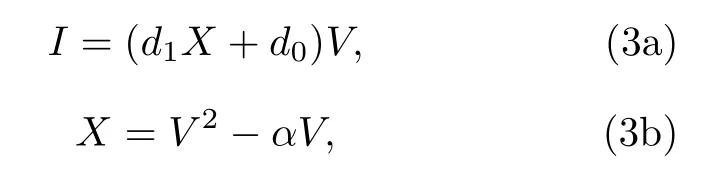
其中X,V,I为静态变量.将 (3b)式代入 (3a)式可得到该忆阻器DCV-I关系式、静态电导GM和微分电导σD的表达式分别为

根据 (4)式,当V以0.1 V 的步长从0 V 增至6 V,分别得到对应的电流响应I,电导值GM以及微分电导值σD,如图2 所示.图2 黑色、红色、蓝色曲线分别代表I,GM及σD随电压的变化规律.

图2 N 型LAM 电学特性曲线Fig.2.N-type LAM electrical characteristic curves.
观察图2 可知:该LAM 的DCV-I特性曲线呈N 型变化趋势,满足设计要求.在工作点A(2 V,2 mA)至B(4 V,1.6 mA)之间为NDR 区域,并在黑色和蓝色曲线上标记.在合适的直流偏置下,N型LAM工作在NDR区域,如Q点为(3 V,1.8 mA),可以产生周期振荡.
神经元在神经网络中负责处理树突端传来的信号并决定是否发放脉冲.因此为了设计基于N 型LAM 的人工神经元,需要设计一个动态电路,在施加相应激励后能够产生丰富的动力学行为,才能应用在SNNs 单元电路的搭建.为了搭建一个基于N 型LAM 的人工神经元电路,仍需要一种储能元件,即电感器或电容器.依据小信号分析法[23],可以推导出上述所提出的N 型LAM 数学模型的小信号阻抗函数等效为[34]

其 中a1=1,a0=1/τ,b1=d1X+d0,b0=[d1V·(2V—α)+d1X+d0]/τ.因 此,N 型LAM在NDR 区域的小信号等效电路如图3 所示,从而可以确定搭建神经元电路所需的另一种储能元件为电感.

图3 N 型LAM 小信号等效电路Fig.3.N-type LAM small-signal equivalent circuit.
3 人工神经元设计及理论分析
3.1 神经元结构
通过第2 节理论分析可知,一个N 型LAM 与电感串联后构成的二阶动态电路在施加相应外界激励后,可以产生振荡行为,因此该电路可应用于SNNs 单元电路的搭建.本节将设计并搭建一个基于N 型LAM 的神经元电路,以产生丰富的神经形态行为.图4 为基于第2 节提出的N 型LAM 搭建的人工神经元电路图,其中vD为神经元输入信号,忆阻器两端电压v为输出信号.

图4 基于N 型LAM 的神经元电路Fig.4.Neuron circuit based on the N-type LAM.
根据N 型LAM 的数学模型以及电感元件的伏安关系,将基尔霍夫定律应用于图4 所示电路,可以得到电路的状态方程为

3.2 霍普夫分岔分析
为了研究输入信号vD和动态元件电感L对图4 中电路动力学行为的影响,本节将采用霍普夫分岔分析和数值分析方法研究该电路产生周期振荡的条件和规律.
令 (6) 式中dx/dt=0,di/dt=0,可得该电路的平衡点为
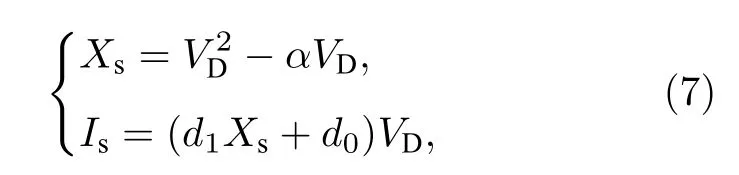
其中Xs,Is分别为N 型LAM 处于稳定状态下的状态变量以及流经N 型LAM 的电流.当VD=3 V时,可得电路的平衡点为(—18 V,1.8 mA).若该平衡点不稳定,x和i将围绕该平衡点产生极限环.
通过求解雅可比矩阵Jc(VD,Xs,Is)的特征值可得到平衡点不稳定的条件,即图4 中神经元电路的振荡条件[23].基于 (6)式,雅可比矩阵可表述为

使用Matlab 进行数值仿真分析,图5(a)给出了在30 mH≤L≤600 mH 范围内,雅可比矩阵Jc(VD,Xs,Is) 的特征值的轨迹,其中箭头指示了当L增大时,特征值轨迹的运动方向,蓝色与红色曲线分别代表雅可比矩阵的特征值λ1和λ2.
观察图5(a)可以发现,当Re(λ1,2)=0 时,L0=33 mH,该点即为霍普夫分岔点.根据霍普夫分岔点的定义,该点两侧会发生不同的动力学行为,即稳定点和极限环行为的分岔点.因此,当VD=3 V时,若图4 中电路要发生振荡,需要满足条件:L≥33 mH,即粉色划线区域.
为了研究不同电感值下电路振荡对应的直流激励范围,设置L以1 mH 的步长从35 mH 增至600 mH,求解不同电感下对应的霍普夫分岔点,得到振荡区域对应的直流激励取值范围,如图5(b)所示.

图5 (a) 在VD=3 V 且30 mH ≤ L ≤ 600 mH 范围下,雅可比矩阵特征值的轨迹;(b) 逐步增大电感,人工神经元电路可振荡条件下,VD 范围变化趋势Fig.5.(a) The trajectory of the Jacobian matrix eigenvalues with VD=3 V and 30 mH ≤ L ≤ 600 mH;(b) with the artificial neuron circuit can oscillate,the VD range changes trend whereas the inductance increase gradually.
观察图5(b)可知,随着电感的增大,电路可发生振荡的激励范围也更广,但始终保持在2 V≤VD≤4 V 范围内(因为只有在NDR 区域才可能发生振荡).经过以上分析可以得知,图4 中的人工神经元电路在合适的激励和L值下(图5 中的粉色划线区域),可以发生振荡行为.
为了进一步研究满足振荡条件后,不同工作点下振荡频率随电感取值的变化规律,设置VD分别为2.5,2.8,3.0 和3.5 V,电感L以1 mH 的步长,从45 mH 增至600 mH,得到振荡频率f随电感的变化趋势,如图6 所示.

图6 不同直流激励选择下,逐步增大电感时振荡频率变化曲线 (a) VD=2.5 V;(b) VD=2.8 V;(c) VD=3.0 V;(d) VD=3.5 VFig.6.The oscillation frequency change curves when the inductance is gradually increased under different DC excitations:(a) VD=2.5 V;(b) VD=2.8 V;(c) VD=3.0 V;(d) VD=3.5 V.
观察图6 可以发现:随着电感L的增大,振荡频率始终保持减小的趋势.当L较小时,振荡频率的下降速度较快;当L较大时,振荡频率的下降速度开始减缓.
4 人工神经元的神经形态行为
4.1 全或无放电行为
在神经细胞中,瞬时的单一激励只要达到一定强度,就会引起神经细胞产生一个尖峰信号,而这个能引起反应的最弱刺激称之为阈强度,只要刺激低于阈强度,神经细胞就无反应,这个过程也称作“全或无定律”.在图4 所示电路中,输入两个幅值分别为1 V 和3 V,持续时间均为0.1 ms 的脉冲信号,得到该神经元电路的“全或无”放电行为,如图7 所示.
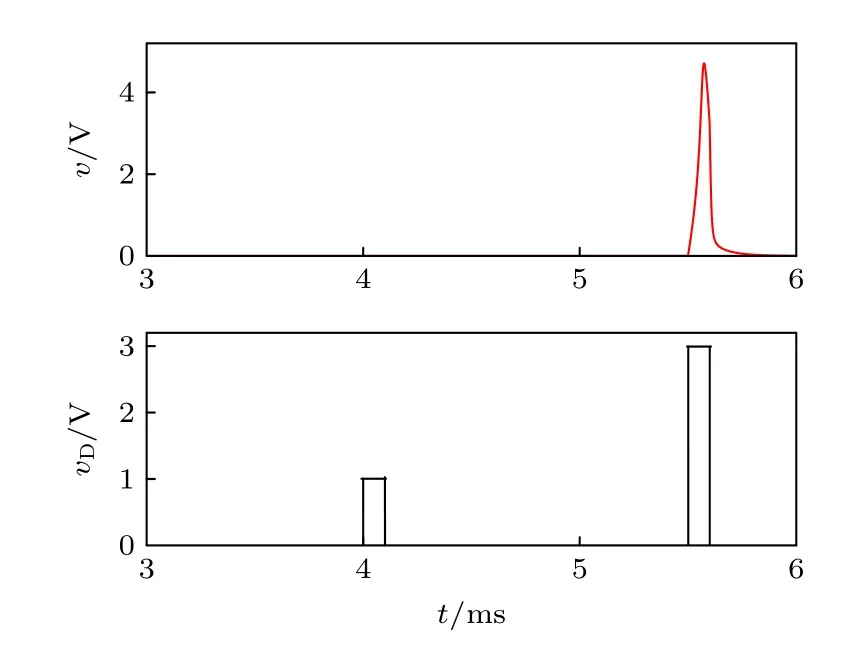
图7 N 型LAM 神经元电路的“全或无”行为Fig.7.The“all-or-nothing”behavior of N-type LAM neuron circuit.
图7 表明,当输入脉冲幅值为1 V 时,电路并不能产生尖峰信号,即“无”行为;当脉冲幅值为3 V 时,由于超过阈强度,神经元电路开始产生尖峰信号,即“全”行为.
4.2 尖峰、簇发、周期振荡
神经元在接受刺激后传递信号,传递一次信号,就称之为一次发放,也就产生一个尖峰.因此,脉冲发放也被认为是神经元最基本的神经行为.模拟神经元的脉冲发放行为,设置幅值为3 V,频率为2 kHz,占空比为0.01 的脉冲波作为激励信号,得到神经元电路的输出波形,如图8(a)所示.观察图8(a)可以发现,由于脉冲宽度过小,电路产生的尖峰幅值过小,神经元处于静息状态.为了更全面研究神经元传递信号的行为,设置输入脉冲占空比分别为0.1,0.4,0.6,0.8 和1.0,绘制不同脉冲宽度下,神经元电路输出信号的瞬时时域波形如图8(b)—(f)所示.
观察图8(a)—(f)可知,占空比为0.1 时,神经元电路产生了一个尖峰,尖峰幅值为2.5 V;随着占空比升至0.4,神经元电路一个周期内产生了两个子脉冲,且主脉冲的幅值升至4.7 V;当占空比增至0.6 时,电路在单周期内产生了3 个子脉冲;当占空比为0.8 时,神经元电路在1 个周期内产生了4 个子脉冲.这种单个周期内呈现为多个子脉冲的现象称之为“脉冲簇”.根据图8(b)—(e)可以发现,脉冲簇中子脉冲的数量与激励脉冲的脉冲宽度成正比,脉冲宽度越大,子脉冲的数量越多,且每个子脉冲的幅度不尽相同,但时间间隔相同、分布均匀.当激励脉冲的占空比增至1.0 时,此时的激励脉冲相当于直流输入电压,神经元电路产生了周期振荡现象,并且围绕着Vs=3 V 这一平衡点附近振荡,振荡频率为11.11 kHz.

图8 不同占空比的脉冲激励下,神经元电路的发放行为波形 (a)占空比=0.01;(b)占空比=0.1;(c)占空比=0.4;(d)占空比=0.6;(e)占空比=0.8;(f)占空比=1.0Fig.8.The firing behavior waveforms of the neuron circuit under pulse excitation with different duty ratios:(a) Duty ratio=0.01;(b) duty ratio=0.1;(c) duty ratio=0.4;(d) duty ratio=0.6;(e) duty ratio=0.8;(f) duty ratio=1.0.
事实上,当激励脉冲幅值在一定范围内取值,N 型LAM 神经元电路都可以得到相似的发放行为.脉冲幅值的选取与N 型LAM 的局部有源工作区间有关,需设置在(2 V,4 V)区间内.
4.3 触觉神经元的频率特性
生物感受器在接收到外界刺激后会产生电压经过传入神经进入大脑皮层,当刺激强度低于大脑最大承受强度时,外界刺激信号使得感受器进入兴奋状态,此时神经元的振荡频率与刺激强度成正相关;而一旦刺激强度超过“阈值”时,大脑会启动保护性抑制机制,继续增大刺激强度,触觉神经元的频率会随着刺激强度的增大而减小,大脑进入抑制保护状态.图9(a) 展示了生物感受系统结构示意图.将4.1 节提出的N 型LAM 神经元电路用于模拟生物感受系统中触觉神经元的频率特性,图9(b)给出了该触觉神经元的结构示意图,根据刺激强度的不同幅值,进而改变输出信号的频率,其中压力传感器可将外界刺激转换为电压信号VD[32].
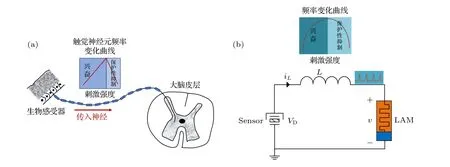
图9 (a)生物感受系统结构示意图;(b)基于N 型LAM的人工触觉神经元结构图Fig.9.(a) Schematic diagram of the biological sensor system;(b) the structure diagram of the artificial tactile neuron based on the N-type LAM.
根据3.2 节分析可知,电感值过小会导致产生振荡行为的激励取值范围过小.为了能够在较大的激励范围内观察所设计触觉神经元的频率特性,设置串联电感L=300 mH,令直流激励VD分别为2.1,2.5,2.9 和3.5 V,分析不同直流激励对振荡行为的影响规律,仿真结果如图10 所示.

图10 L=300 mH 时,不同直流激励下人工神经元电路中N 型LAM 两端电压v 的瞬时时域波形Fig.10.The instantaneous time-domain waveforms of the voltage across the N-type LAM in the artificial neuron circuit under different DC excitations with L=300 mH.
观察图10 可以发现,在可振荡的直流激励范围内,N 型LAM 两端电压总是保持在VD附近振荡,与理论分析一致.当VD=2.1,2.5,3.0 和3.5 V时,LAM 两端电压v的振荡频率分别为2.17,2.83,3.00 和2.71 kHz.因此,v的频率随着VD的增大,先增大后减小.为了进一步验证以上规律,图11 绘制了当L分别为300 mH 和500 mH 时,直流激励VD从2.1 V 增至3.85 V 时振荡频率的变化规律,图中箭头表示频率的变化方向.
观察图11(a)可以发现,随着直流电压的增大,振荡频率从f1=2.15 kHz 处先增大后减小,并在电压VD=2.92 V 时达到峰值,此时fmax=3.01 kHz;此后不断降低直至f2=2.22 kHz.图11(b)与图11(a)频率变化规律相似,峰值频率fmax=2.13 kHz,其对应的电压值VD=2.93 V.

图11 不同电感下,递增直流电压下振荡频率变化曲线 (a) L=300 mH;(b) L=500 mHFig.11.Oscillation frequency varies as a function of DC voltage under different inductances:(a) L=300 mH;(b) L=500 mH.
以上仿真结果说明本文所设计的人工神经元电路输出信号的频率随激励强度的变化规律与生物感受系统中的触觉神经元极为相似,验证了所设计电路的可行性与正确性.
5 硬件实现
5.1 N 型LAM 电路仿真器
为了证实基于N 型LAM 人工神经元的可行性,本节给出了N 型LAM 的硬件电路仿真器,原理图如图12(a)所示,其中包括4 通道TL084 运算放大器(U1A,U1B,U1C),用于实现加减法和积分计算;AD633 乘法器(U2,U3)用于实现乘法计算;AD844运算放大器(U4) 用于实现电流传输.图12(b)展示了实验设备图,包括示波器,可调直流电源,信号发生器和N 型LAM 硬件电路仿真器.图12(a)中①部分使用AD844 使流入N 型LAM 的电流i与vw成正比;②部分实现 (2) 式中状态变量x的求解,输出端vx的值与状态变量x成正比;③部分实现了电导GM的运算,输出端vG与电导值GM成正比;④部分执行乘法运算;最后vw连接在Rin的另一端,流入N 型LAM 的电流i满足:

基于图12(a)中的硬件仿真器结构图,可以得到各个端口的输出信号表达式为
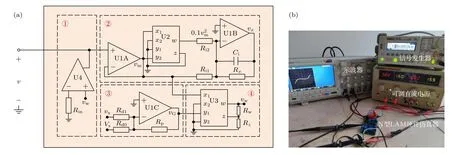
图12 (a) 基于N 型LAM 的硬件仿真器原理图;(b) 实验设备图Fig.12.(a) Schematic diagram of hardware emulatorof the N-type LAM;(b) diagram of experimental equipments.

表1 中给出了硬件仿真器中各器件参数配置.将表1 中参数代入 (11) 式计算可得τ=10—5,α=9,d1=10—4,d0=2.4 × 10—3,与 (2)式完全一致.

表1 硬件电路参数数值Table 1.Hardware circuit parameter value.
为了观察该N 型LAM 仿真器的NDR 区域,在N 型LAM 两端直接施加一个中低频三角波信号,以1 kHz 的频率从0 V 逐步增至6 V.由于端口电压vw与电流i成正比,因此通过测量电压vw可以间接获得忆阻器电流测量数据.通过测量端口vm与vw,得到如图13(a) 所示准静态DCV-I特性曲线;另外测量端口vG,得到如图13(b)所示电导随电压变化曲线.
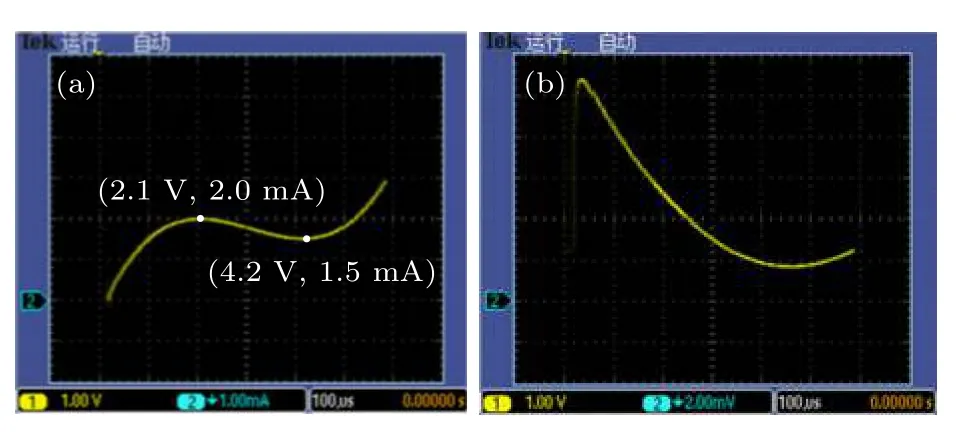
图13 (a) 实验测量N 型LAM 硬件仿真器的DC V-I 特性曲线;(b) 实验测量N 型LAM 硬件仿真器电导变化曲线Fig.13.(a) Experimental measurement of the DC V-I characteristics curve of the N-type LAM hardware emulator;(b) experimental measurement of the conductance change curve of the N-type LAM hardware emulator.
观察图13(a)可以发现,实验测量的NDR 区域为2.1 V<V<4.2 V,1.5 mA<I<2 mA,图13(b)中电导变化曲线与图1 仿真分析基本一致.与数值分析相比,尽管该实验结果存在一定的误差,但该误差在可允许范围内,证实了该N 型LAM 仿真器的可行性.实验误差可能源于电子元器件误差和电子设备的测量误差.
5.2 神经元动力学行为
为了硬件实现基于N 型LAM 的人工神经元,需将N 型LAM 仿真器与电感、电压激励串联,如图14 所示.

图14 人工神经元仿真器电路结构图Fig.14.Circuit structure diagram of artificial neuron emulator.
当输入信号vD包含两个幅值分别为1 V 和3 V,脉冲宽度为0.1 ms 的脉冲信号,实验测量得到人工神经元的“全或无”行为,如图15 所示,图中蓝色和黄色曲线分别为输入脉冲和神经元电路输出波形.

图15 实验测量得到人工神经元的“全或无”行为Fig.15.Experimentally measured the“all-or-nothing”behavior of artificial neuron emulator.
观察图15 可以发现,输入脉冲幅值为1 V 时,由于低于阈强度,电路输出信号幅值过小;脉冲幅值为3 V 时,电路产生1 个尖峰.与仿真结果相比,在1 V 脉冲信号激励下,仿真结果观测不到电压变化是因为脉冲信号持续时间仅为0.1 ms.如果略微增大激励脉冲持续时间,如0.2 ms 和0.3 ms,在仿真结果中也能观测到小的波动.因此,仿真与实验的误差是响应时间上的差异造成的.硬件仿真器采用电路元器件对模拟信号进行实时处理,而数字仿真的运算速度受计算机处理器影响.因此,硬件仿真器与数字仿真相比,具有实时性优势.
模拟神经元的脉冲发放行为,设置激励vD为幅值3 V 的脉冲信号,逐步增大脉冲宽度,实验结果如图16 所示.

图16 增大脉冲宽度,实验测得神经元的发放行为波形 (a)占空比为0.15;(b)占空比为0.40;(c)占空比为0.65;(d)占空比为0.85Fig.16.Increasing the pulse width,the experimentally measured neuron firing behavior waveforms:(a) Duty ratio is 0.15;(b) duty ratio is 0.40;(c) duty ratio is 0.65;(d) duty ratio is 0.85.
观察图16 可以发现,脉冲激励的占空比为0.15,0.40,0.65 和0.85 时,神经元电路发放的脉冲簇中分别有1,2,3,4 个子脉冲.与仿真分析相比,产生的簇放现象是一致的,验证了神经元电路的可行性.
采用直流电压源VD代替图9(b)中的压力传感器,进一步实验验证人工神经元的可行性.选取直流激励VD=3 V,令电感分别为30,39,47,100,200 和300 mH,观察不同电感下,人工神经元电路输出波形,实验结果如图17 所示.
观察图17 可以发现,当直流激励VD=3 V时,电感为39 mH,电路无法产生振荡;电感增大至47 mH 时,电路起振.实验测得的可振荡电感范围与理论分析结果具有一定的偏差,这与电阻的精确性以及实际电感器件中存在寄生电阻相关.电路元件值的误差,导致仿真器的模型系数发生了偏差;实际电感中存在的寄生电阻会对电路中的信号造成衰减,因此产生实验结果误差.图17(c)—(f)表明,随着电感的增大,振荡频率始终保持减小的趋势,这一结果与图6 中的仿真结果相对应.
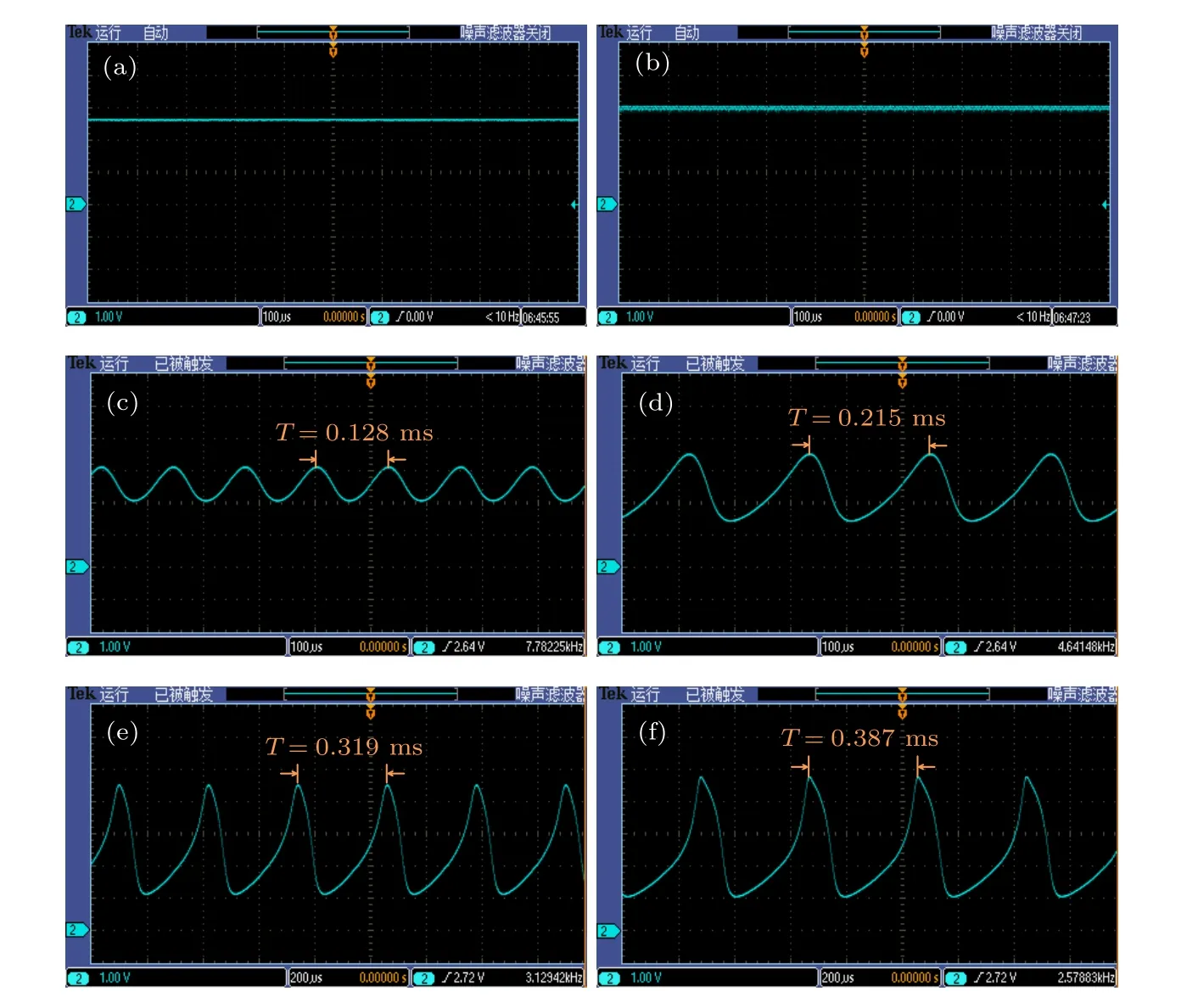
图17 直流偏置VD=3 V 时,不同电感选择下实验测得人工神经元电路输出v 的瞬时时域波形 (a) L=30 mH;(b) L=39 mH;(c) L=47 mH;(d) L=100 mH;(e) L=200 mH;(f) L=300 mHFig.17.The experimentally measured instantaneous time-domain waveforms of the artificial neuron circuit output v under different inductances with the DC bias VD=3 V:(a) L=30 mH;(b) L=39 mH;(c) L=47 mH ;(d) L=100 mH;(e) L=200 mH;(f) L=300 mH.
为了进一步验证该电路的频率特性,电感取值300 mH,分别选取直流电压VD=2.5,2.8,3.5,4.0,4.4,4.8 V,实验测量得到输出信号v的瞬时时域波形如图18 所示.
观察图18 可以发现,增大直流激励,v的频率先增大后减小.为了更加直观地验证仿真分析中频率变化特性,电感取值分别为330 mH 和470 mH,直流激励以0.05 V 的步长逐步增加至电路不发生振荡,利用实验测试所得频率值,通过Origin 绘制出v的频率变化曲线,如图19 所示.

图18 电感L=300 mH 时,不同直流偏置选择下实验测得N 型LAM 两端电压v 的瞬时时域波形 (a) VD=2.5 V;(b) VD=2.8 V;(c) VD=3.5 V;(d) VD=4.0 V;(e) VD=4.4 V;(f) VD=4.8 VFig.18.The instantaneous time-domain waveforms of the voltage v across the N-type LAM measured under different DC bias selections with the inductance L=300 mH:(a) VD=2.5 V;(b) VD=2.8 V;(c) VD=3.5 V;(d) VD=4.0 V;(e) VD=4.4 V;(f) VD=4.8 V.
观察图19 可以发现,当电感为330 mH 时,电路产生周期振荡对应的激励范围为2.61—4.45 V;当电感为470 mH 时,激励范围为2.33—4.30 V.由于图9(b)电路中电感L存在分压,导致激励范围超过NDR 区域.在两种L取值下,v的频率变化趋势与仿真完全一致.当直流激励超过一定阈值时,电路会产生保护性抑制行为;继续增大激励强度,振荡频率与其呈负相关.随着电感L的增大,电路产生振荡时对应的激励范围更广,但振荡频率却逐渐减小,该特性与仿真分析结果一致.因此,上述实验结果证实了基于N 型LAM 人工神经元的可行性.

图19 两种电感选择下,递增直流激励实验测得v 的频率变化曲线 (a) L=330 mH;(b) L=470 mHFig.19.The experimentally measured frequency characteristics increasing the DC excitation gradually under two different inductances:(a) L=330 mH;(b) L=470 mH.
6 总结
本文提出了一种简单的N 型LAM 数学模型并给出了其电路实现,通过数值仿真和硬件实验验证了其N 型NDR 特性并确定了其局部有源区间.通过对N 型LAM 串联电感,进一步构建了二阶人工神经元电路,并通过仿真分析和实验验证了所设计方案的可行性.研究结果表明:基于N 型LAM的二阶神经元电路可模拟生物神经元的神经形态行为,如全或无、尖峰发放、簇放和周期振荡.此外,该神经元电路的频率特性与生物触觉神经元具有较高的一致性,存在“保护性抑制行为”.因此,本文工作为N 型LAM 在神经形态计算中的应用奠定了一定的理论基础.

