一种近似最优的大规模MIMO检测算法

周 围 陈星宇* 马茂琼 冉静萱 彭 洋

1(重庆邮电大学通信与信息工程学院 重庆 400065)2(重庆邮电大学移动通信技术重庆市重点实验室 重庆 400065)

0 引 言

随着移动用户数量每年都在急剧增长，用户渴望更快的互联网接入速度以及即时访问多媒体服务，这就需要更高效的传输速率、更高的频谱效率以及更好的移动性[1]。因此，研究人员提出了5G网络来解决上述问题，应用高效的技术[2]部署在5G网络中，例如设备对设备(D2D)通信、超密集网络(UDNs)、频谱共享、毫米波(mmWAVE)和大规模多输入多输出(MIMO)。第五代(5G)通信系统在6 GHz以下采用经典的大规模MIMO技术，在无线电信道中具有散射和多径传播特性。由于天线的尺寸较小，较大的阵列更容易在更高的频率实现和封装[3]。因此，大规模MIMO检测技术适合在厘米波或者毫米波系统中发挥作用。

最早的大规模MIMO检测器可以追溯到2008年，Vardhan等[4]提出了一种基于似然上升搜索的大规模MIMO检测器。使用大量天线导致的直接问题是涉及高复杂度计算量，在接下来的几年里，一些研究者提出使用局部搜索和置信传播算法来实现接近ML的性能。

近年来，大规模MIMO[5]渐渐进入研究者们的视线中。文献[6]表明，在发射天线数量较多的情况下，可以利用信道硬化现象来抵消小尺度衰落特性，当接收天线数N远大于发射天线数K时，信道的每一列渐近正交，信道矩阵逐渐变为对角占优矩阵，信道硬化现象占主导地位。因此，一些传统的算法如ML、MMSE又成为研究热点[7]，ML算法是具备理论性最优性能的算法，但其穷尽搜索的方式应用在大规模矩阵时复杂度会随着天线数增加而剧增，而MMSE线性检测涉及到高维度的矩阵求逆运算。近些年来，针对如何避免MMSE检测涉及到的矩阵求逆方案分为三类。

第一类为梯度搜索的方法，如共轭梯度[8]等，这类利用每一层进行梯度搜索的方法，优点是性能较好，但每一次迭代需要计算相应的梯度，极大地增加了计算量。第二类是多项式展开逼近近似解的方法，如诺伊曼级数展开[9]，利用诺伊曼级数展开项近似逆矩阵，此类方法当级数展开(i>2)时，算法的复杂度仍然很高。第三类是通过迭代的方式一步步逼近近似解的方法，如牛顿迭代[10]、高斯-赛德尔迭代[11]、超松弛迭代[12]等。牛顿迭代的方法在满足文献[10]的条件时，能实现快速的收敛，但在初始估计时需要更多的计算。高斯-赛德尔迭代的方法在基站与用户单天线数比值为1时，依然具有良好的性能，但由于算法内部顺序迭代结构，很难并行实现。超松弛迭代的方法复杂度低，在基站天线数与用户数为较大比例时依然具备最优性能，缺点与高斯-赛德尔相似，很难并行实现，并且有一个不确定的松弛参数。

本文提出了一种近似最优MMSE线性检测算法，不需要进行复杂的矩阵求逆运算，与高斯-赛德尔和超松弛检测不同，提出的加权两阶段信号检测由两个半迭代组成，然后通过加权系数将两个半迭代合并在一起，得到迭代解，从而降低了算法的复杂度，并通过SD算法良好的搜索性，优化WTS方案的收敛速度，有效地减少了多用户干扰。数值结果表明，优化后的WTS方案在误码率以及收敛速度上都优于传统的高斯赛德尔和超松弛类算法。此外，通过少量的迭代可以获得最佳的性能。

1 系统模型

假设大规模MIMO基站(BS)端服务于K个单天线用户。BS处设置N根接收天线，K个用户与N根BS处天线之间的信道增益构成矩阵Hc∈CN×K，该矩阵为平坦瑞利信道，满足独立同分布。对K个用户的信息位进行编码，sc=[s1,s2,s3,…,sK]T为从用户端发送K×1维的符号向量，其中sk∈Q是第k个用户发送的符号向量，Q是调制符号集。令Hc∈CN×K为独立且同分布的信道矩阵，因此BS处收到的N×1维信号矢量表示为：

yc=Hsc+nc

(1)

式中：nc为加性白噪声向量，其项满足高斯分布均值为0，方差为σ2IN。本文的重点在上行链路检测，将复信道矩阵转化为相同的实信道矩阵得到：

y=Hs+n

(2)

2N×1维的实数接收、发送、噪声矢量分别为y=[{yc}T,{yc}T]T、x=[{xc}T,{xc}T]T、n=[{nc}T,{nc}T]T，H表示2N×2K维的等效信道增益矩阵：

(3)

MMSE检测的主要思想是最小化传输的符号s与估计信号HHy之间的均方误差，信号检测的目的是在BS处对信号矢量y无差错地经过判决恢复出发送信号矢量s，实验证明，用MMSE检测算法对所有K个单天线用户的发射信号向量进行估计，效果是最优的。表达式如下：

(4)

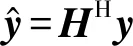
W-1=(G+σ2IK)-1

(5)

式中：G=HHH为gram矩阵。将接收到的信号向量代入式(2)，得到第i个用户发送的估计符号为：

(6)

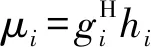
(7)

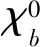
2 方案设计

2.1 WTS方案

在大规模MIMO系统中，信道矩阵H的列是渐近正交的，因此W为正定的Hermite矩阵[13]。为了避免复杂的矩阵求逆，加快收敛速度，本文提出了一种WTS信号检测方案，采用两个半迭代，并将两个半迭代与一个加权系数相结合，迭代求解如下：

1) 由于W是严格对角占优的Hermite矩阵，并且W的对角占优程度越高，收敛速度越快，我们将W分解为W=D+L+LH，其中L和D分别为严格的下三角矩阵和对角矩阵。为了加快迭代收敛性，本文首先提出两个不含松弛参数的对称半迭代：

(8)

(9)

前半段迭代可写为：

(10)

后半段迭代可写为：

(11)

D+LH和D+L是针对三角矩阵求逆变换，比直接求逆更简单。

2) 为了减少近似误差，提高收敛性能，将式(10)、式(11)合并，得到：

(12)

式中：θ为加权系数，通过数次模拟实验，本文将θ设置为θ=(K/M)2；i为方案迭代次数；s(0)为K×1维的初始解。

本文提出WTS的信号检测方案可以迭代地逼近MMSE所需复杂矩阵求逆，优点是更快的收敛速度以及更低的复杂度。现有的GS迭代、NS展开、SOR迭代利用类似的方法避免矩阵求逆，然而本文提出的WTS方案与现有的一些迭代法不同，相互对称的迭代矩阵中不需要松弛参数，这说明该方案在实际应用中更具备鲁棒性。此外，与GS和SOR算法相比，WTS方案更具备灵活性，当加权系数θ=0时，为SOR迭代，当加权系数θ=1时，为GS迭代。

2.2 改进的WTS方案

最速下降搜索[14]作为一种梯度搜索的方法，优点是在迭代初期会有很好的逼近解的趋势，作为优化算法对低复杂度的WTS方案进行优化处理，在不增加复杂度的背景下对本文所提方案进一步加快收敛速度，并且实现逼近MMSE误码率曲线的性能，改进的WTS方案如下所示：

步骤1设置初始解，根据矩阵的对角近似原理，W为正定Hermite矩阵，随着天线数的增加，呈逐渐对角占优趋势，因此设置初始解为：

(13)

因为D-1为对角矩阵求逆，所以矩阵求逆复杂度降低，把s(0)作为最速下降法的初始解。

步骤2将本文提出WTS方案第二次的前半次迭代用SD算法来表示，第二次WTS前半次表示为：

s(1)+(D+L)-1r(1)

(14)

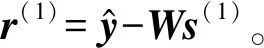
r(0)-μp(0)

(15)

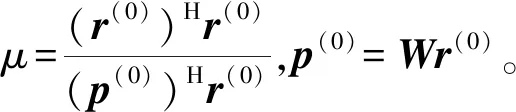
s(3/2)=s(0)+μr(0)+(D+L)-1(r(0)-μp(0))

(16)

接下来将优化后的前半次迭代的解代入后半次迭代：

(17)

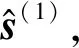
步骤3进行(i-1)次WTS方案，此处可以根据实际情况设置不同的i，如下所示：

(18)

(19)

(20)

2.3 近似对数似然比的计算

优化后的WTS方案通过迭代得到最优解向量，代替MMSE直接求逆运算，实现了复杂度从O(K3)下降到O(K2)的变化。为了解码得到精确值，可以通过在信道译码时使用LLR软信息。通过式(6)不难发现，第一步为了算出SINR，须对矩阵W进行求逆，复杂度又一次提高，下一步是降低求逆带来的计算量。因为信道发生硬化，利用矩阵主对角线占优的特性，用W-1化简为D-1来做下一步运算，信道增益以及方差可以表示为：

(21)

(22)

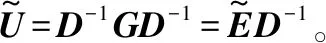
3 复杂度与仿真结果分析

3.1 复杂度分析

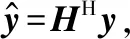
(1) 初始解与第一次迭代。初始解需要2K次实乘运算，首次迭代分别计算r(0)、p(0)、μ需要4K2、4K2、4K次实乘运算，结合式(16)及式(17)，初始解与首次迭代合计需8K2+10K的实乘运算。

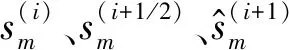
改进的WTS方案所有实乘次数由以上三部分组成，共需(12K2+12K)+(i-1)(2K2+4K)次乘法。 因此，提出的改进的WTS方案的总复杂度为O(K2)。

3.2 仿真结果分析

为了进一步证明提出方案的性能以及可行性，以直接矩阵和对角元素求逆的MMSE检测误码率性能为比较基准，在MATLAB R2016b软件上进行了仿真实验。假设CSI已知，表1为仿真背景。

表1 仿真背景

图1为本文提出WTS检测方案与Neumann级数展开检测、MMSE检测、Gauss-Seidel检测之间的复杂度比较。可以发现，当i=2时，WTS方案的复杂度明显低于MMSE检测算法，略低于Gauss-Seidel检测算法。当i=4时，WTS方案的复杂度与Gauss-Seidel检测基本相同，并且明显优于Neumann级数展开法与MMSE检测。

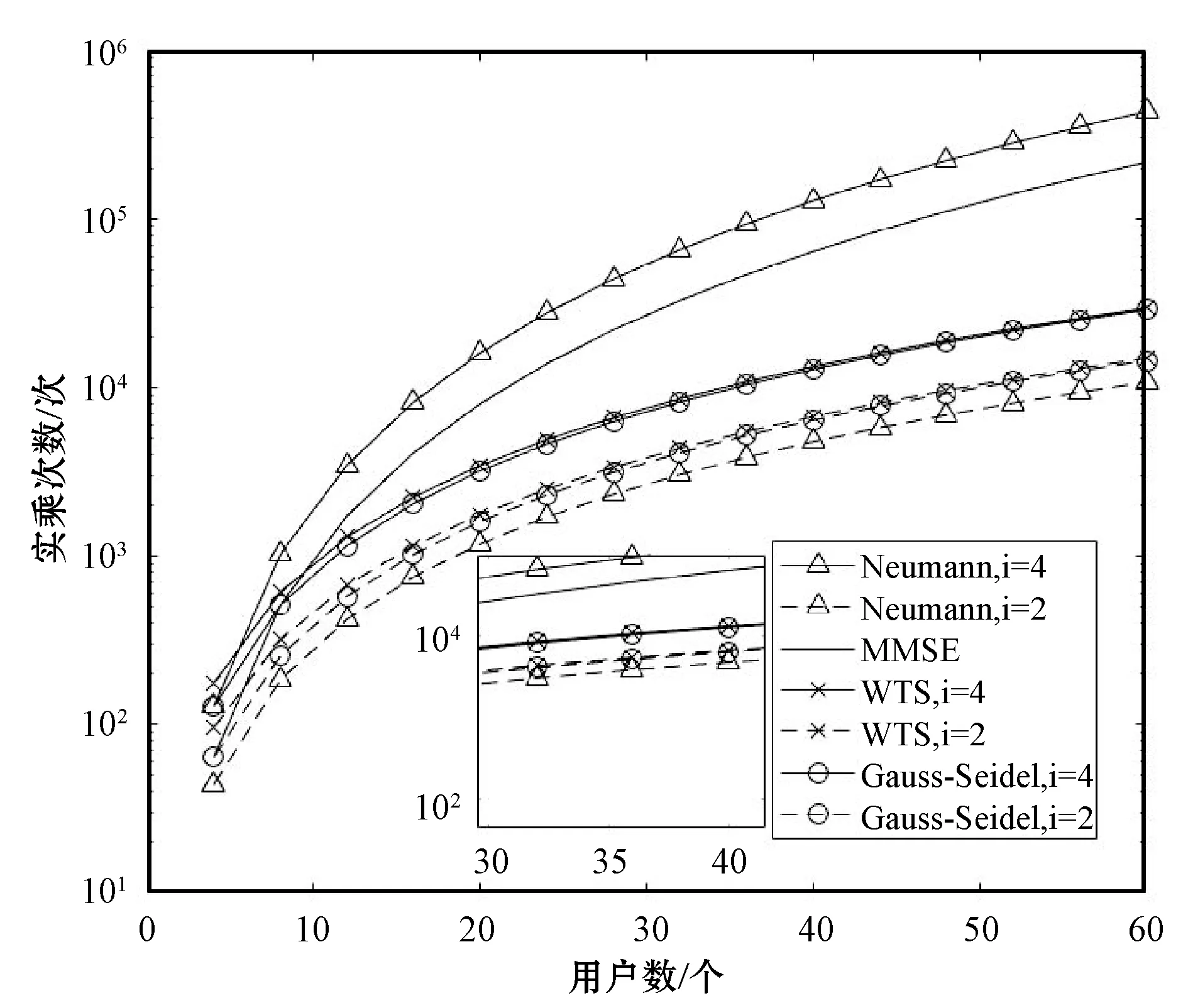
图1 算法之间复杂度对比

图2设置收发天线数为128×16规模的阵列，下图为差错性能BER(Bit Error Rate)曲线，对比了Neumann级数展开检测、Gauss-Seidel检测、MMSE精准求逆和本文提出的WTS方案在软判决中的性能。可以看出，本文所提方案不仅收敛快，BER性能同样优于Gauss-Seidel检测以及Neumann级数展开检测，当i=2时，逼近MMSE最优性能。

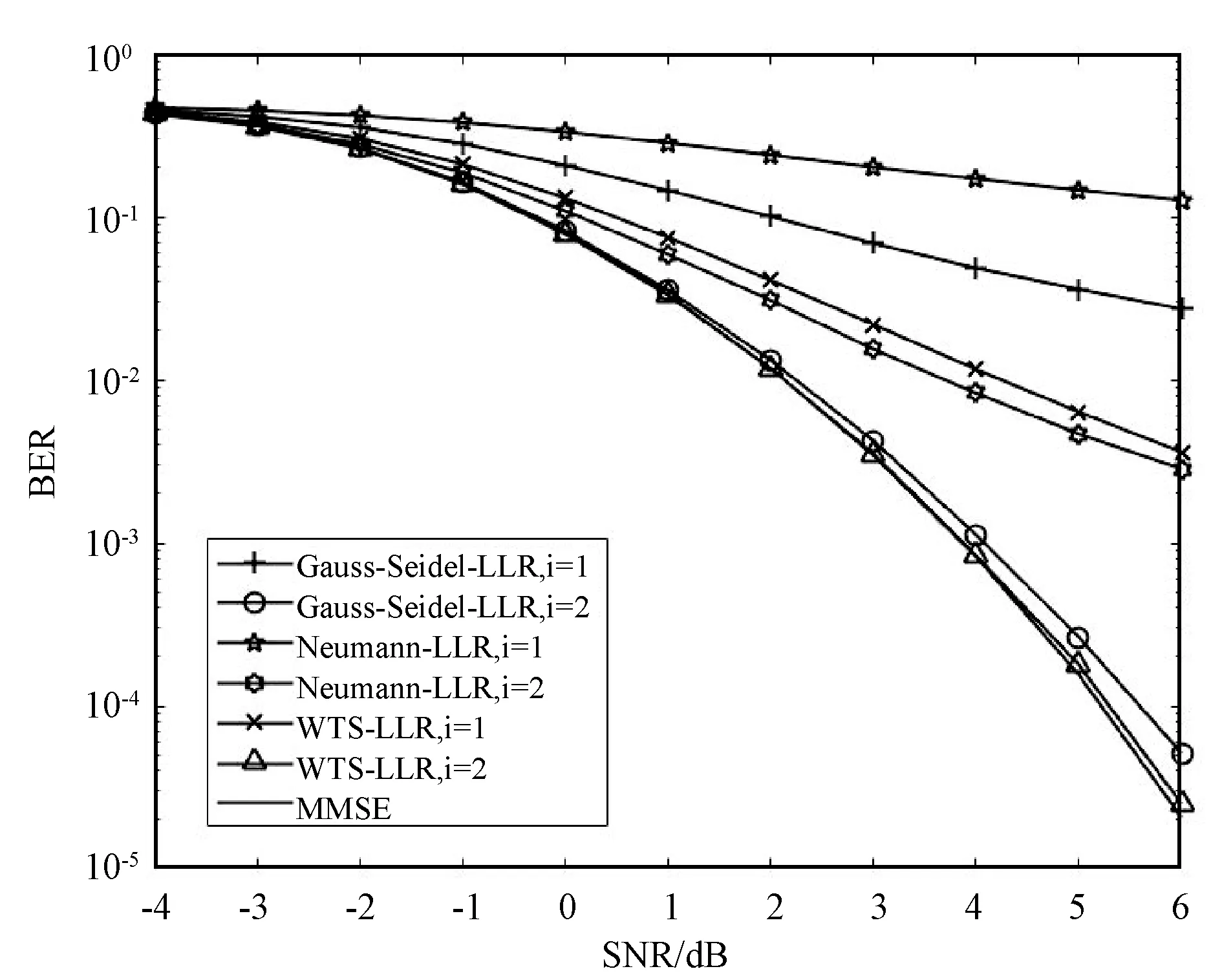
图2 WTS方案与不同算法软输出BER比较

图3中仿真规模同样设置为128×16根天线，列举了各种方案与MMSE算法的BER比较，并在信道译码中采用软判决。采用优化后的WTS方案与传统的检测算法做比较，如图3所示，当迭代次数增加，基于Neumann级数展开的信号检测器、基于Gauss-Seidel的信号检测器以及优化后的WTS方案的误码率性能都有所提升，并且提出的方案性能明显优于其余算法。当SNR=6 dB且i=1时，优化后WTS方案的BER能达到2.6×10-5，从图2可知，未优化的WTS方案在相同仿真背景下BER仅能达到3.6×10-3左右，优化后的WTS方案在性能上有极大的提升，通过一次迭代就逼近MMSE检测曲线，与MMSE检测BER只相差0.1×10-4左右。当i=2时，优化后的WTS方案已经与MMSE曲线基本重合。与图2中的未优化WTS相比，优化后的WTS方案明显收敛速度更快了。容易得出，优化后的WTS方案不仅比WTS方案更快收敛，而且BER性能优于Neumann级数展开法以及Gauss-Seidel迭代等传统算法，不超过两次迭代就能逼近MMSE的最优检测。

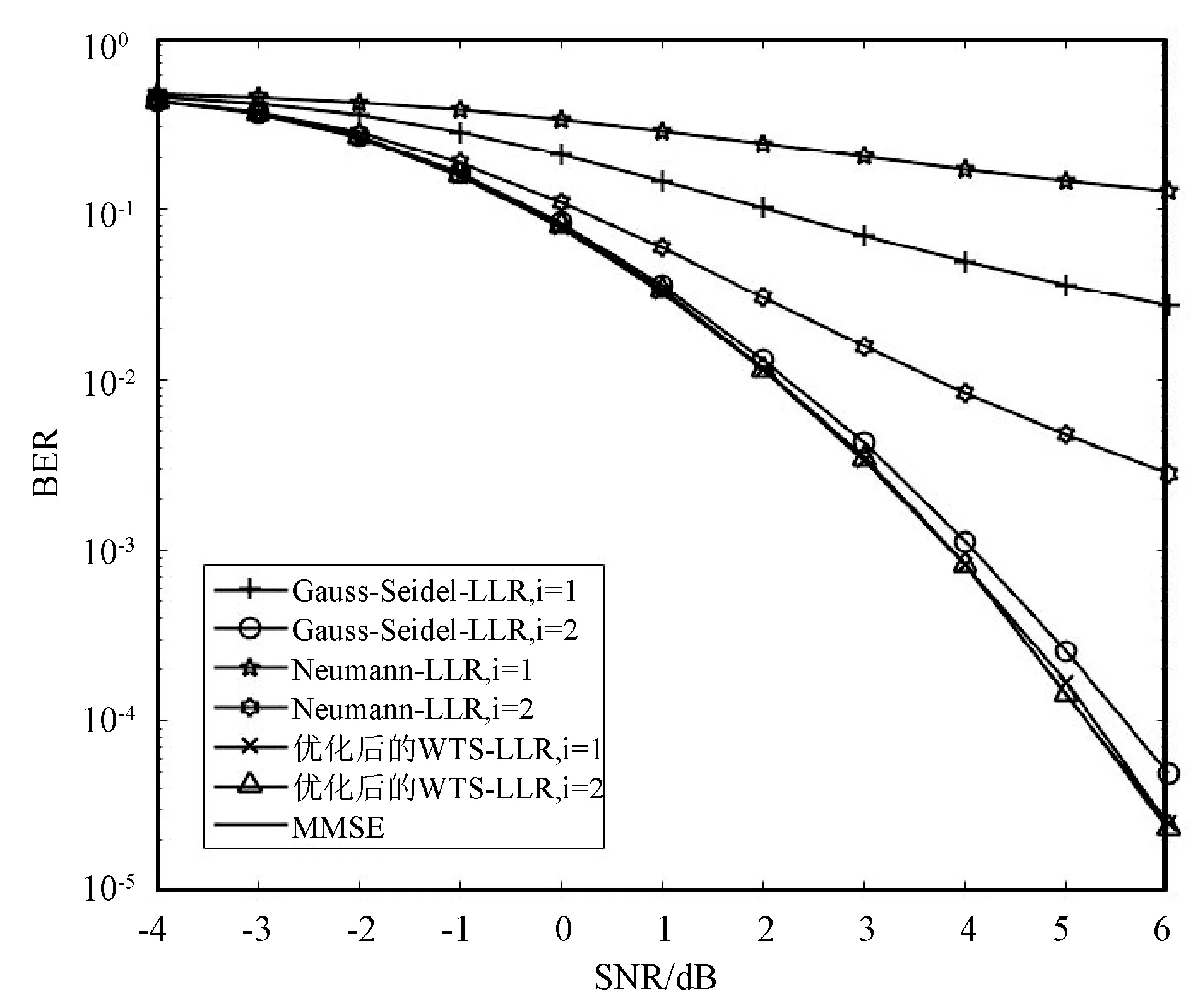
图3 优化后WTS方案与不同算法软输出BER比较

图4为提出的优化WTS方案与未经优化的WTS方案之间收敛性能比较，即误比特率BER在定量分析SNR的情况下与迭代次数的关系。可以看出，当信噪比逐渐提高，本文提出的两种方案的BER有明显的变化，未经优化的WTS需要2～3次迭代达到平稳，而优化后的WTS方案仅仅通过1～2次迭代便接近最优性能，收敛速度得到明显的提升。

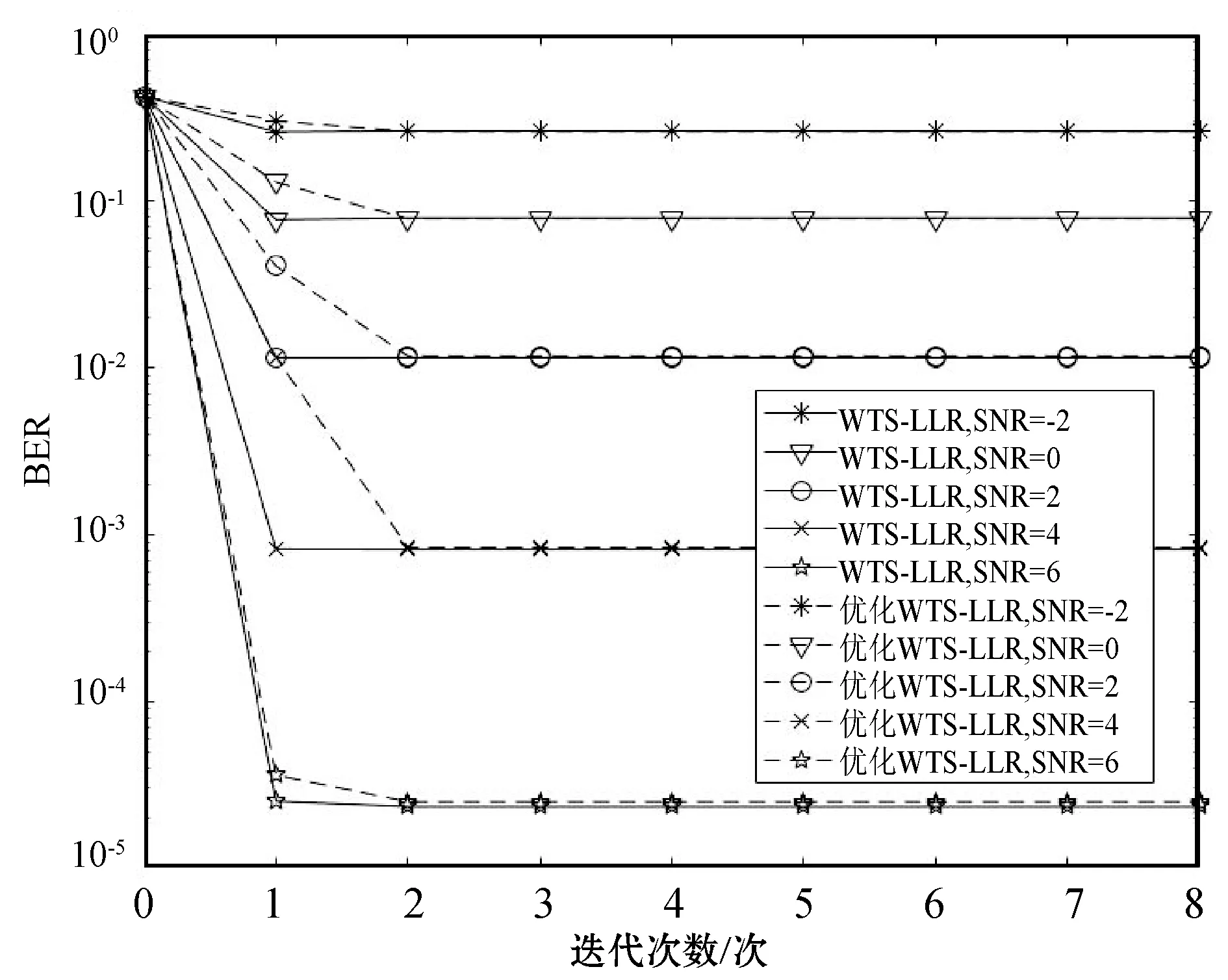
图4 不同SNR的两种方案与迭代次数的关系

4 结 语

本文首次把WTS方案应用于大规模MIMO软输出信号检测，通过加权系数将两个半迭代合并在一起，并利用SD算法的快速收敛性对WTS算法进行进一步改进，在算法的收敛性与复杂度之间进行新的权衡，代替了MMSE算法中的直接求逆运算，复杂度从O(K3)下降到O(K2)。本文对提出WTS方案进行优化，进一步提升了算法的收敛性，再将优化后的WTS方案采用近似对数似然比的方法应用在软判决中，最后对BER性能以及收敛性能仿真，并与一些传统算法作对比。结果表明，本文提出的改进的WTS方案在保持较低复杂度的前提下，仅通过少量迭代就能达到最优的MMSE线性检测性能。