基于Voronoi 序列采样的加筋壁板优化设计
于宝石,王志祥,王 婕,李海阳,张大鹏
(1.国防科技大学空天科学学院,长沙 410073;2.空天任务智能规划与仿真湖南省重点实验室,长沙 410073;3.北京宇航系统工程研究所,北京 100076)
薄壁加筋结构由于其较高的比刚度和比强度而广泛应用于航空航天结构[1⁃2],如运载火箭的燃料贮箱[3]、导弹的级间段[4]等。此类结构在受载时失稳破坏往往先于强度破坏,所以其稳定性问题一直是研究的热点。薄壁加筋结构直接关系到航空航天结构的服役安全和轻质化水平[5⁃6],特别作为主承力结构,轴压载荷下其结构分析与轻量化设计对降低飞行和发射成本具有重要意义。
对于薄壁加筋结构的轻量优化问题,众多学者采用传统的梯度类优化算法求解并获得了较为理想的优化结果[7],但对于高维设计变量、模型复杂的结构,传统优化方法又面临难以收敛到全局解、计算量过高导致优化效率较低等问题。针对上述问题,具备快速预测和算法适用性强等优点的代理模型技术受到广泛关注,并被成功应用到结构优化设计中[8⁃10]。目前,常用的代理模型方法包括多项式响应面、Kriging 模型以及径向基函数(Radial ba⁃sis function,RBF)等。Jin 等[11]详细对比了多种常用的代理模型方法,指出径向基函数较好兼顾了计算效率与计算精度。Gutmann[12]对径向基函数进行了更为详细的介绍。Mullur 等[13]为进一步提升模型近似精度,提出了一种改进的径向基函数。Wang 等[14⁃17]基于径向基函数近似模型对薄壁加筋柱壳后屈曲优化设计开展了大量的研究。郝鹏等[2⁃3,18⁃22]结合代理优化方法与等效刚度模型,对加筋柱壳进行优化设计,后续又基于缺陷敏感性分析开展优化研究。但上述研究的优化方法均依赖初始近似建模的全局精度,针对多极值问题,容易陷入局部最优解。龙腾等[23⁃24]针对飞行器多学科设计优化中传统静态代理模型方法难以保证全局近似精度与计算效率较低的问题,提出了一种动态径向基函数代理模型的优化策略。王志祥等[25]将径向基函数与多岛遗传、非线性二次规划算法相结合,提出一种序列近似优化方法,并在蒙皮桁条结构的优化中取得理想结果。上述研究的序列采样策略均未有效兼顾全局近似精度与局部开发效率,实现局部与全局加点的动态平衡。然而,针对复杂结构,如何进一步提升基于代理模型序列近似优化方法的全局最优性与优化效率,仍是当前研究的重点。
Voronoi 法是计算几何领域内一种重要的几何结构,常常被应用于全局区域检测与路径搜索[26⁃27]。Jiang 等[28]将Voronoi 法引入优化流程中,提出了一种分步辅助序列采样方法,具有较好的全局近似精度。Xu 等[29]提出了基于Voronoi 法和交叉验证的稳健误差追踪序列采样方法,并对比几种序列采样方法,具有更高的优化效率与鲁棒性。上述研究均表明,Voronoi 法在改善样本点空间分布均匀性,进而提高近似模型全局近似精度方面具有显著优势,但将Voronoi 法应用到基于代理模型的序列优化中的研究相对较少。
为综合平衡序列采样的探索和开发性能,提高近似模型优化效率,本文开展了基于Voronoi 法序列采样的研究,并成功应用到加筋壁板的优化设计中。首先,对轴压载荷下加筋壁板结构的屈曲特性进行分析,基于Python 语言建立了结构参数化模型,分析了在不同腹板高厚比下网格规模对结构屈曲特性的影响规律,根据分析规律,结合结构自身特点,依据腹板高厚比动态调整网格划分,平衡了计算精度和优化效率。然后,基于Voronoi 法与径向基函数代理模型,提出了一种序列近似优化方法,针对加筋壁板结构,获得了可行的优化解。最后,对比文献[19]中的优化方法,结果表明本文方法具有更高的优化效率与全局精度。
1 加筋板有限元建模与优化问题
1.1 加筋壁板有限元建模与分析
如图1 所示,加筋壁板模型主要由蒙皮、桁条与端框构成。蒙皮外侧沿纵向分布3 根“几”形桁条,内侧上下两端分布“L”形端框,桁条与端框截面形式及参数如图2 所示。基于Python 语言对高600 mm、宽600 mm 的加筋壁板结构进行参数化有限元建模,为模拟结构板壳特性,采用壳单元划分网格。为获得轴压作用下结构的极限载荷,分别建立“L”形弹性边界与端框对接。分别建立参考点与上下弹性边界节点进行刚性耦合,下参考点固支约束,上参考点约束除轴向位移外的其他自由度。匀速施加10 mm 强制位移,综合考虑分析效率与计算精度[30],将加载速度设置为200 mm/s。轴压载荷作用下,加筋壁板的破坏形式为对应载荷最高点结构的失稳模式,失效载荷即为位移⁃载荷曲线最高点处的极限载荷。模型采用钛合金材料,其密度为4.45×106kg/mm3,弹性模量为110 GPa,泊松比为0.3,屈服应力825 MPa,强度极限895 MPa,延伸率为10%。基于传统工程设计方法,加筋壁板初始设计结构参数如表1 所示。表中M、Fcr0分别表示初始设计结构质量和极限载荷,其他变量含义如图2 所示。精度与效率之间的平衡,成为结构优化设计中不可忽视的问题。针对上述问题,本文对加筋壁板结构进行网格无关性分析,总结分析网格规模对结构承载性能和失稳模式的影响规律,进而实现兼顾计算效率与分析精度的动态有限元建模。

图1 结构有限元模型Fig.1 Structural finite element model

表1 加筋壁板初始设计及变量取值范围Table 1 Initial design of stiffened panels and range of variable values

图2 加筋壁板结构组件截面尺寸Fig.2 Section dimensions of stiffened panel structural assemblies
图3 与表2 分别给出了不同蒙皮单元大小时位移⁃载荷曲线、结构失稳云图、极限载荷以及计算耗时。随蒙皮单元尺寸的减小,极限承载能力逐渐降低并收敛到一稳定值。当蒙皮单元尺寸小于15 mm×15 mm 时,结构失稳波形基本相同,继续加密网格对极限载荷的影响小于0.224%,而计算耗时增加

表2 不同蒙皮网格尺寸下结构整体失稳情况Table 2 Overall instability under different skin mesh sizes

图3 不同蒙皮网格尺寸下结构的位移-载荷曲线Fig.3 Displacement-load curves of structures with different skin mesh sizes
针对薄壁板壳结构,单元网格划分的疏密程度将严重影响结构轴压载荷与失稳模态的分析精度[31]。如何在大规模的优化计算中保持模型计算71.8%。因此综合考虑计算精度与效率,在后续的优化计算中蒙皮单元尺寸确定为15 mm×15 mm。
对应结构优化迭代过程中尺寸参数的变化,若采用统一的网格划分精度将会造成个别样本参数下网格过疏或过密,相应地导致仿真误差较大或计算成本较高。基于上述问题,以表1 所示的初始结构尺寸为基准,在不改变桁条腹板横截面积下(即hfb×tfb不变),分析不同腹板高厚比(αfb=hfbtfb)下网格密度比对加筋壁板承载能力和失稳模式的影响规律。
图4 为不同网格密度下结构承载能力随桁条腹板高厚比变化曲线及结构整体失稳时桁条位移云图。其中U 为桁条位移。由图可知,在αfb≤52时,不同网格密度下结构承载能力与失稳模态基本相同。但随αfb继续增加,结构承载能力下降,桁条腹板出现失稳波形。这主要是因为,在αfb较小时,增大腹板高度即提升了桁条横向弯曲刚度,桁条临界失稳应力提高,桁条呈现整体失稳模式。而当αfb逐渐增大后,轴压下桁条腹板抵抗面外变形的刚度降低,桁条腹板会先于整体发生局部失稳,从而使得结构承载能力下降。且随着腹板单元层数Nfb增多,承载能力下降趋势更加明显并趋于收敛。这进一步说明在αfb较大的情况下,较少的单元层数会导致计算精度严重下降,无法反映出极限承载力变化规律与桁条局部失稳模态。

图4 不同网格密度下结构承载能力随桁条腹板高厚比变化曲线Fig.4 Curves of structural load-carrying capacity with height-thickness ratio of webs under different mesh densities
基于上述分析,在优化历程中根据桁条尺寸参数在桁条腹板高度方向上进行网格划分如下

式中:Nfb表现为随αfb变换的分段函数。当αfb≥52时,较少的单元划分存在较高的计算误差;当αfb≤52 时,3~5 层单元足够满足计算精度,过度的划分又会降低计算效率。对比设定单一网格密度,依据腹板高厚比的网格划分兼顾了计算效率与分析精度,为后续的优化迭代节约了大量计算成本。
1.2 优化问题
以桁条、端框截面尺寸参数及蒙皮厚度等13个结构尺寸参数为设计变量,以满足设定承载能力为约束,开展加筋壁板轻质优化设计。其中,设计变量均为连续变量。针对本结构的优化问题,其数学模型可表示为

式中:x表示结构设计参数,取值范围参考表1。M(x)及Fcr(x)为结构参数取值x时对应的结构质量和极限载荷。F∗cr为目标极限载荷,设定为1.13×106N。
2 序列近似优化方法
针对上述加筋壁板的后屈曲轻质优化,考虑到问题具有多变量、高耗时等特性,本文以径向基函数近似模型为主干,提出了一种基于探索和开发并行采样的序列近似优化方法。
2.1 径向基函数近似模型
不失一般性,单位立方体空间Ω=[0,1]m中,给定一组训练样本集

具体建模过程可参考文献[20,35]。基于此径向基函数近似模型,可较为准确地反映加筋壁板结构参数与极限承载性能的近似映射关系,进而开展后续优化设计。
2.2 序列近似优化方法
序列采样策略的基本思想是根据当前样本点及近似模型相关信息,获得下一个(组)采样点,以期提高近似模型全局/局部近似精度,引导近似优化算法高效快速搜索到最优解。基于此思想,本文提出了基于Voronoi 法的序列采样策略。其中,基于Voronoi 法的探索策略通过动态识别稀疏样本点区域并添加采样点,进而提高近似模型的全局近似精度;基于近似模型与组合优化算法的开发策略通过在潜在最优点处加点,并利用近似最优解加速算法收敛,进而提升近似模型的局部近似精度。
2.2.1 基于Voronoi 法的探索策略
基于Voronoi 法的探索策略可以归纳为以下几个步骤:


式中:dom(xi,xj)是被点xi与xj之间连线的中垂线分割的封闭区域,点xi称为多边形ci的中心点,多边形ci中任意一点距其中心点xi的距离都是最近的。
(2)识别加点最稀疏的泰森多边形cs。泰森多边形的边界一般不规则,很难准确描述其形状,Voronoi 法通过Monte Carlo 法构造泰森多边形。向设计空间Rm内生成NRP个随机点,NRP取值为

当Voronoi 图为二维图形时,识别cs过程如图5 所示。其中,cs区域随机点数量最多,覆盖区域最大。

图5 二维Voronoi 图识别cs 示例Fig.5 Two-dimensional Voronoi diagrams identify cs exam⁃ples
(3)在cs中确定新加点xn+1。如前所述,多边形cs可以用一组随机点Ps描述。因此,新加点xn+1可以按照一定的采样准则从随机点集Ps中选取。为尽可能多地获得关于目标函数的信息,cs中采集新点xn+1应距中心点xs尽可能远,即


2.2.2 基于近似模型与组合优化算法的开发策略
基于近似模型与组合优化算法的开发策略可以归纳为以下步骤:
(1)利用当前训练样本集S,采用2.1 节中的数学方法构造RBF 近似模型。
(2)采用多岛遗传算法(Multi⁃island genetic algorithm,MIGA)与非线性二次规划算法(Non⁃linear programming by quadratic Lagrangian pro⁃gramming,NLPQLP)进行内层迭代优化,对RBF模型进行寻优,迭代收敛后获得一个近似最优解x∗以及对应的近似最优目标函数值f͂(x∗),并计算近似最优解x∗的真实响应f(x∗),即

式中:M̂(x)为结构质量的近似模型;F̂cr(x)为极限载荷的近似模型。
(3)将近似最优目标函数值f͂(x∗)与真实响应值f(x∗)代入收敛判断,满足收敛条件则结束优化,否则将此近似最优解x∗作为新采样点,与其真实的响应值一起更新到样本集中,即S=S∪[x∗,f(x∗)]与n=n+1,进而提高近似模型的局部近似能力。
2.3 算法整体框架
本文提出的序列近似优化方法基于径向基函数近似模型,在每轮迭代中通过探索与开发策略序列采样,以期不断提高近似模型的全局与局部精度,并通过并行计算新采样点,实现加快算法搜索效率与缩短计算时长的目的。算法整体框架如图6 所示。

图6 序列近似优化流程图Fig.6 Flowchart of sequence approximate optimization method
利用初始样本点构建的近似模型需进行精度检验,通过检验模型的均值与R2值等确定满足精度要求的最小初始样本规模nmin。不满足精度要求则增大样本集规模重新采样,直至构建出满足近似模型精度的初始样本集。在优化策略收敛判断中,满足如下任一条件时,停止优化。
(1)第k次与第k-1 次迭代的采样点处有限元计算值之间的相对误差,第k次迭代采样点处近似模型预测值f͂(x∗k)与有限元计算值f(x∗k)之间的相对误差,均满足给定的收敛标准ε,如式(12)所示。

(2)序列采样达到最大迭代次数kmax。在迭代过程中,基于Voronoi 法全局加点侧重于改善样本点在空间中的均布性及填充性,进而提高了近似模型全局近似精度。RBF 近似模型预测潜在最优加点侧重于进一步开发局部最优值区域,以期提升近似模型对该区域的局部近似能力。本文所提优化算法综合利用了二者优势,实现全局探索与局部开发的平衡,有效地提升了优化效率。
3 加筋壁板结构轻质优化设计
根据2.2 节所述的序列近似优化方法对加筋壁板结构开展轻质优化。本文采用优化拉丁超立方实验设计方法生成30 个初始样本点(即nmin=30),然后计算对应样本点的极限载荷与结构质量,以此构建初始近似模型。考虑到初始近似模型在最优点处预测不够准确,采用第2 节所述方法进行序列加点。
在相关优化算法的参数设置上,为提高MIGA种群多样性与收敛速度,多岛遗传算法中设置岛数为20,各岛种群数为20,进化代数为40,交叉率为1.0,变异率与迁徙率均为0.01;为提高NLPQLP收敛精度,非线性规划算法设置最小步长为10-4,最大迭代次数为50。
为了验证本文方法的有效性,将本文方法与Wang 等[18⁃21]提出的序列近似优化方法相对比。图7 所示为两种方法在迭代过程中载荷相对误差eFcr和质量相对误差emass。其中,图7(a)为本文方法误差收敛曲线,在迭代20 次后,极限载荷与质量的相对误差均小于0.01,误差趋于收敛。对比图7(b)文献方法误差收敛情况,在迭代32 次后,相对误差趋于收敛,说明了本文优化策略能在迭代过程中更快的收敛,具有更高的优化效率。
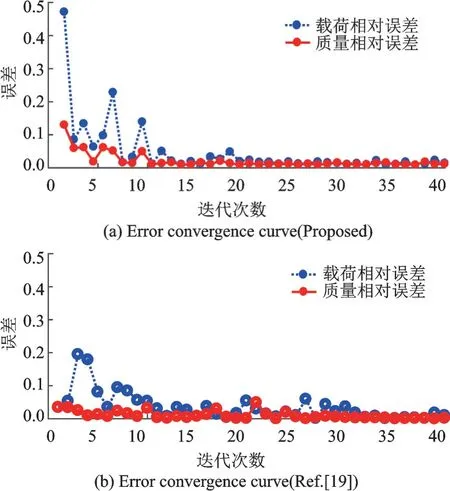
图7 优化历程中的误差Fig.7 Error in optimization process
图8 所示为目标函数与性能约束函数的迭代历程曲线,本文方法在经历25 轮迭代后,结构极限承载能力满足设计需求,且结构质量也趋于收敛。对比文献方法,在得到几乎相同的优化结果的情况下,本文方法收敛更快,进一步验证了本文序列近似优化方法具有更高的优化效率。

图8 加筋壁板结构质量及极限载荷迭代历程Fig.8 Iteration curve of structural mass and limit load
图9 为两种优化方法中近似最优加点与已有样本点的最小距离随迭代次数的收敛曲线。对比曲线收敛情况,文献[19]的优化方法在局部区域内迭代加点并快速收敛,而本文优化方法在每次迭代时先向样本点分布稀疏区域加点,再于迭代中快速收敛到局部区域。这说明基于Voronoi 法动态序列加点策略有助于跳出局部最优区域,是在全局搜索后再预测最优解,有效提高了模型的预测精度,具有更好的潜在最优区域开发能力。

图9 两种优化方法新加点与已有样本点最小距离迭代曲线Fig.9 Iterative curve of minimum distance between new point and existing sample point in two optimization methods
经本文序列近似优化后,在轴压载荷加载到4.7 mm 时,结构整体失稳破坏,对应的极限载荷为1.134×106N,得到结构质量为9.810 kg。在承载力满足设计要求下,结构减重4.742 kg,减轻初始设计结构质量的32.6%。表3 列出了所提方法和文献方法得到最优设计的比较结果,采用本文优化策略,只经过25 次迭代,结果收敛,较文献方法优化效率提升了40.5%。在最优解方面,两种方法最优解相对误差仅为0.028%。且由于本文方法具有更高的全局近似精度,在初始样本点的选取上,仅选取了30 个样本点,相较文献中的优化方法减少了40%,进一步节约了计算成本。
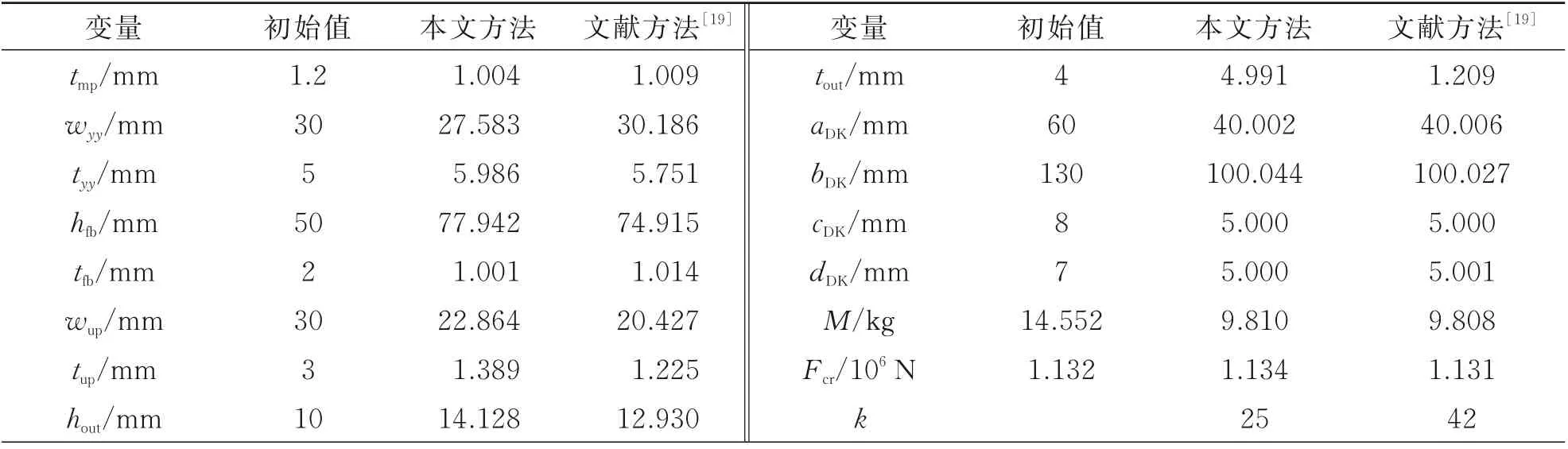
表3 设计变量初始值与最优值Table 3 Comparison of initial desing and optimal variables
结合图10 与文献方法最优解处轴压位移⁃载荷曲线及整体失稳时位移云图对比情况,由图可知,两条曲线的线性前屈曲段与非线性后屈曲段几乎重合,极限载荷近似相同,且结构整体失稳模式也基本相同。表4 对比了两种方法获取的优化结构在整体失稳时的应力S云图与等效塑性应变(Equivalent plastic strain,PEEQ)云图,本文方法获得的结构应力分布与塑性形变与文献方法得到的基本一致,桁条与蒙皮连接处应力较大,最大应力分别为961 MPa 和935 MPa,蒙皮中心与桁条局部区域进入塑性形变,蒙皮最大等效塑性应变分别为0.8%和0.7%,中间桁条最大等效塑性应变分别为2.2% 和2.3%。两种方法对比结果验证了本文提出的序列近似优化方法的有效性。

表4 加筋壁板结构整体失稳时应力云图与等效塑性应变云图Table 4 Stress and equivalent plastic strain cloud diagram of completely buckling stiffened panel

图10 加筋壁板结构轴压位移-载荷曲线及整体失稳时位移云图Fig.10 Loading-displacement curve and displacement cloud diagram of completely buckling stiffened panel
4 结论
本文以加筋壁板结构设计为研究背景,开展了基于Voronoi 法的加筋壁板高效序列轻质优化方法研究。主要工作与结论可总结如下:
(1)探究了加筋壁板结构蒙皮与桁条腹板网格划分对结构屈曲特性的影响规律,建立了网格划分方式与桁条腹板高厚比的对应关系,兼顾了建模精度与计算效率。
(2)提出了一种基于Voronoi 法的序列采样策略,实现了探索和开发动态平衡的并行采样。并将此方法应用于加筋壁板的后屈曲轻质优化中,结果表明,相较于初始设计,在满足极限载荷约束的情况下,优化后结构有效减重了32.6%,验证本文方法的有效性。
(3)将本文提出的序列近似优化方法与现有的仅添加近似最优点方法进行了对比,结果表明,本文方法提高了模型的预测精度,有效缩减了初始样本集的规模,降低了迭代次数,提升了优化的效率,并且具有更好的全局探索与潜在最优区域开发能力。

