PBX 炸药损伤本构模型及其工程运用

黄垂艺，时 岩，金朋刚，陈 凯

（1. 南京理工大学机械工程学院，江苏 南京 210094；2. 西安近代化学研究所，陕西 西安 710065）

1 引言

高聚物黏结炸药（（PBX）是一种以高能炸药为主体，与黏结剂、降感剂和增塑剂等辅助成分混合制成的高能钝感的混合炸药，其使用场景中受到多种载荷的作用，可能产生各种损伤，影响其力学性能和可靠性。PBX 材料是武器装备系统中最薄弱的环节。因此，对PBX 材料的力学性能及损伤特性进行研究，对武器装备的设计、可靠运用有着重要作用。

近年，世界相关学者对PBX 材料的研究报道主要集中在准静态及动态加载下的力学性能的研究与分析。张子敏［1］、屈可朋［2］、孙文旭等［3］通过准静态实验和霍普金森压杆（SHPB）试验获得了PBX 材料在一定应变率范围内的力学性能，并用相关本构模型进行描述。目前国内外对于PBX 材料研究的重难点在于其受到冲击载荷后的损伤特性及其演化规律，其中的困难在于PBX 材料内部的损伤难以捕捉与表征，以及由于工艺、设备、批次不同导致的初始损伤的无规律分布；此外，由于PBX 材料的损伤特性及其演化规律与应变率、温度有关，缺乏考虑全面的变量来表示其细观破坏与其宏观力学性能响应之间的关系。因此，目前对PBX 材料损伤的相关研究主要是采用专业仪器捕捉其破坏图像，并进行分析总结，增进对其破坏过程的认识［4］。陈鹏万等［5］对低速气炮加载后的PBX 炸药的冲击损伤形貌进行了显微观测；刘本德等［6］用X 射线限位层析成像、CT 图像序列结合数字图像处理算法对SHPB 冲击试验后的样本损伤裂纹进行提取、三维重构与分析。

目前对PBX 材料的研究与评估中，相比试验，数值仿真能展现更多细节信息，是一种效果更优的研究手段。同时，商业有限元软件给PBX 材料的研究提供巨大的便利性，如材料本构的二次开发。虽然PBX 材料的力学行为和损伤特性没有相应的模型可对其进行准确描述［7］，但由于宏观上PBX 材料的力学响应和橡胶材料、高分子材料及推进剂材料的力学响应相似，且对上述材料的研究更为深入和完整，可从上述材料的相关研究中参考有意义的部分对PBX 材料的数值仿真开展进一步研究。

本工作依托PBX 材料的动态力学性能试验结果，在有限元软件ABAQUS 中的材料子程序VUMAT 功能下，以相关学者运用较多的含损伤变量的Z-W-T 本构模型为框架对PBX 炸药进行研究，解决了前人研究存在的拟合参数非多应变率共用的问题；并对PBX 材料的动态力学性能及其损伤与演化过程的损伤变量进行了定义，得到了可以进行可视化损伤云图表示且具备应变率相关性的材料模型，并对PBX 材料进行带壳装药破片撞击仿真与分析，该材料子程序可为后续PBX 材料的力学性能数值实现、损伤表征数值实现及安全性数值评估、装药结构改进的研究提供基础。

2 含损伤变量的Z-W-T 本构模型

Z-W-T 本构模型是由朱兆祥、王礼立和唐志平根据有限粘弹性本构方程和Green-Rivlin 本构理论提出的适用于描述热塑性或热固性高分子材料非线性粘弹性行为的本构模型［8］，已被广泛运用于推进剂材料等粘弹性材料的力学性能表征。

Z-W-T 非线性粘弹性本构模型的积分形式为：

式中，ε为应变；fe(ε)为材料的非线性弹性响应项，E0、α和β是对应的非线性弹性常数，E0单位为Pa；式（1）第二项描述低应变率下的粘弹性响应，E1和θ1分别是其对应的低频Maxwell 单元的弹性常数和松弛时间；第三项描述高应变率下的粘弹性响应，E2和θ2分别是所对应的高频Maxwell 单元的弹性常数和松弛时间，弹性常数的单位为Pa，松弛时间的单位为s。低频和高频Maxwell 单元即为分别负责低应变率和高应变率的弹簧—粘壶组合模型。

早期在对Z-W-T 本构模型进行研究时，所研究的材料在应变达到一定值后，会出现微裂纹损伤。随着应变的继续增大，微裂纹损伤的数量增多，导致材料的抗变形能力削弱，引起材料的弱化和软化。因此对本构模型引入Kachanov 损伤变量［8］，得到：

式中，σ为无损伤应力，Pa；σr为含损伤应力，Pa；D为损伤变量，无量纲。Z-W-T 本构的模型的提出者与早期研究者对D的定义如下：

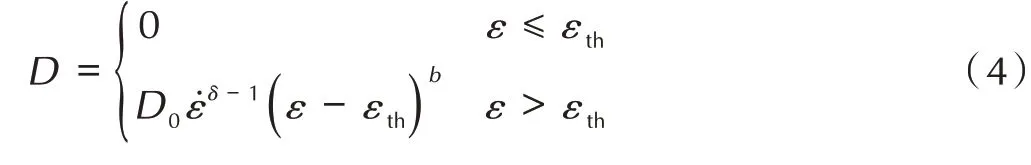
式中，εth为应变损伤阈值，当应变大于该值时出现微裂纹；D0为初始损伤因子；b为损伤应变指数因子；δ为率相关的指数因子；b和δ是材料参数。应变损伤阈值εth在以往的研究中一般定为固定值或0，但根据试验获得的材料本构曲线，该值应该与应变率相关，根据参考文献［9］，应变损伤阈值与应变率的关系应该满足：

式中，A和B为一般参数；ε˙为应变率。

近年来，研究PBX 炸药力学性能的学者在研究过程中将Z-W-T 非线性粘弹性本构模型运用在描述PBX炸药的力学性能中获得了比较好的结果［1-3］。

3 动态力学性能试验

3.1 试验装置

采用SHPB 作为PBX 炸药的动态压缩性能测试装置，如图1 所示。PBX 炸药强度较低，同时由于内部高聚物黏结剂的黏弹性使其具有吸能缓冲效果，导致应力加载过程较为缓慢，不同应变率下动态屈服强度相差不大，失效应变反而相差较大。要有效地获取其具有应变率相关性、非线性黏弹性及应变软化效应的力学性能，对试件应力均匀性、常应变率加载及信号测量准确性提出了较高的要求［10］。因此，从整形器与试件的设计方面加以考虑，设计了不同材料与尺寸的整形器与试件，通过试验筛选合适的组合以满足测试要求。因此，采用波阻抗较低的铝合金作为杆的材料，并采用半导体应变片测量透射信号及将橡胶作为整形器材料。所设计的整形器、试件、子弹及压杆的材料与尺寸见表1。

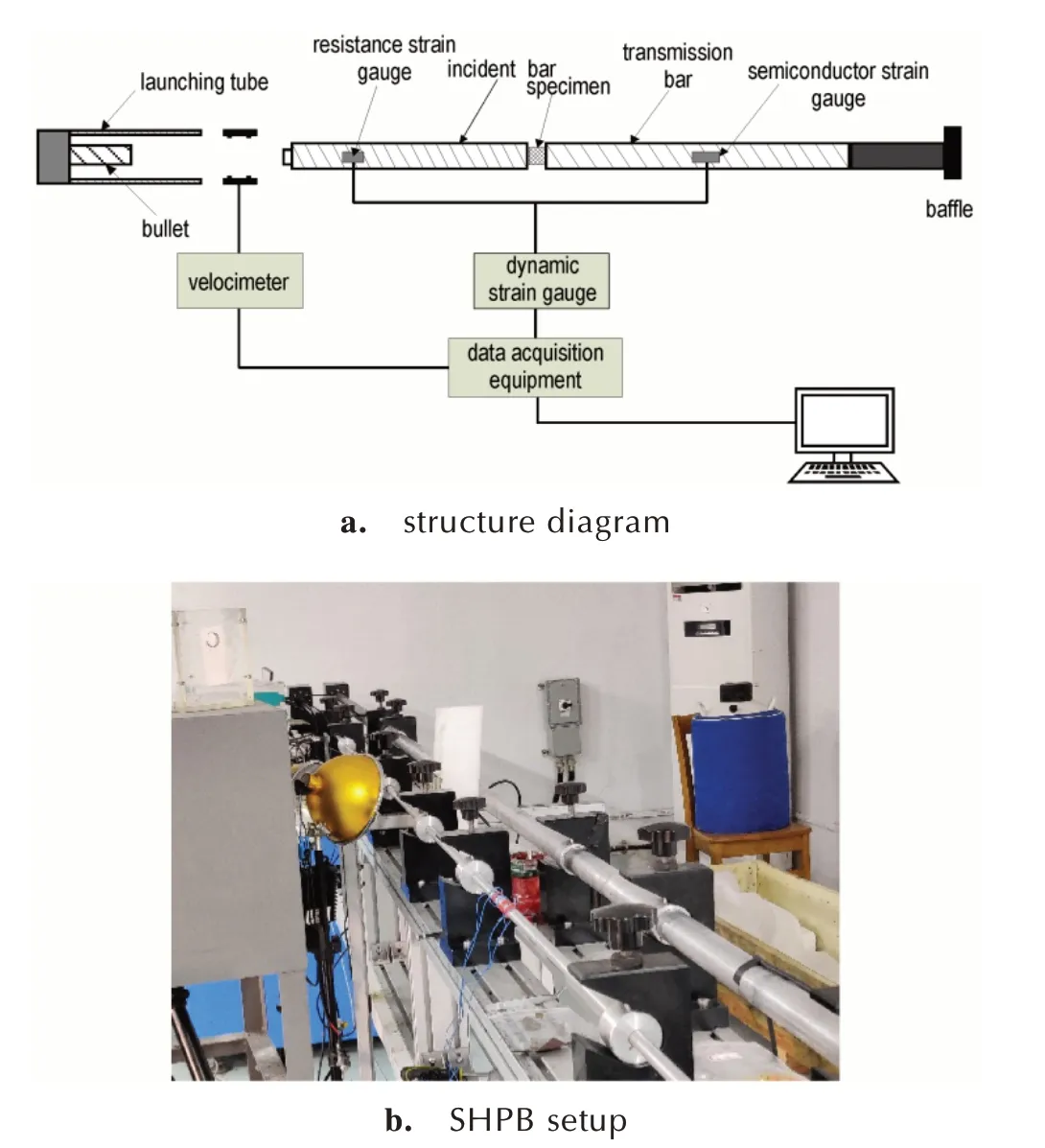
图1 霍普金森压杆（SHPB）动态压缩试验装置Fig.1 Hopkinson dynamic compression test device

表1 SHPB 主要设计参数Table 1 Main design parameters of SHPB

3.2 试验结果与分析

利用SHPB 测量得到入射波、反射波及透射波信号后，通过专门的数据处理软件计算应力-应变曲线及应变率-时间曲线。应力均匀性与常应变率加载是SHPB 准确获取动态力学性能的前提条件，图2 为试验测量得到的入射波、反射波及透射波信号，从图2 可以看出：（1）根据应力均匀性判别条件，试件已达到应力均匀；（2）半导体应变片准确地捕获到了强度较弱的透射信号，为应力、应变及应变率等力学性能参数的正确计算提供了保证；（3）反射波实现了平台波，标志着试件获得了常应变率加载，在图3 所示的应变率-时间变化曲线中得到了印证。

图2 PBX 炸药典型入射波、反射波、透射波信号Fig.2 Signal of incident wave，reflected wave and transmitted wave

图3 PBX 炸药典型应变率-时间曲线Fig.3 Strain rate vs. time curve

图4 所示为PBX 炸药在1300～6100 s-1应变率范围内的应力-应变变化曲线，从图4 可以发现：（1）随着应变率的增高，动态屈服强度从0.96 MPa（1300 s-1）增加到4.52 MPa（6100 s-1），反映了一定的应变率效应；（2）曲线开始阶段，表现出较强的非线性黏弹性，且应力上升较为缓慢。到达屈服后表现为应变软化效应，这是因为材料内部发生损伤及演化，承载能力降低。由于PBX 的非线性黏弹性与应变软化效应，导致其失效应变在应变率范围内变化较大，从1300 s-1冲击作用下的0.18 增加到6100 s-1冲击作用下的0.62，说明PBX 炸药具有较强的韧性与抗冲击破坏能力。

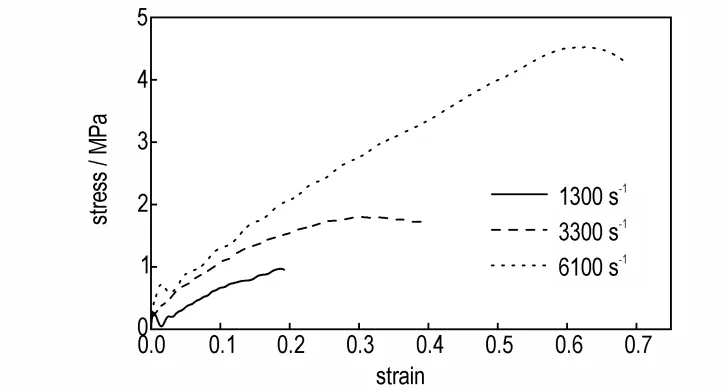
图4 PBX 炸药不同应变率下的应力-应变曲线Fig.4 Stress strain curves of cast PBX under different strain rates

3.3 本构模型参数获取

得到PBX 的力学性能后需要拟合合适的本构参数对其进行表征。Z-W-T 本构模型的相关研究表明，低频Maxwell 单元松弛时间θ1通常是10～102量级，高频Maxwell 单元的松弛时间θ2通常是10-4～10-6量级。本研究所进行的动态力学性能试验仅在10-4s 内完成，代表低频Maxwell 单元的部分没有足够的时间松弛，根据参考文献［2］中的处理方法，忽略代表低频Maxwell 部分的积分项，因此，式（1）可化为式（6）：

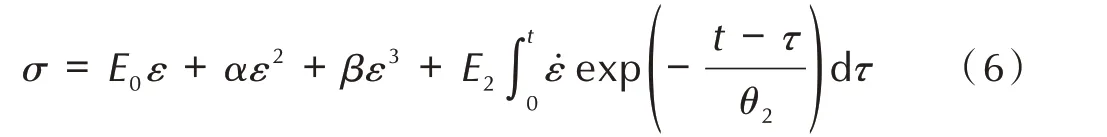
根据参考文献［11］中提及的内容及仿真软件的算例验证方法，作为有限元分析基础的材料应力-应变关系需要是全曲线准确的。试验获得的工程应力应变不能准确地反映材料的应力应变情况，需按照式（7）和式（8）将工程应力应变转换为真实应力应变。图5为转换后的真实应力-应变曲线。

图5 PBX 炸药在不同应变率下的真实应力-应变曲线Fig.5 Real stress-strain curves of PBX explosives at different strain rates

首先，在多个应变率达到损伤之前的真实本构数据基础上，运用Origin Pro 软件与Levenberg-Marquardt优化算法对式（6）中的5 个参数，E0、α、β、E2和θ2，进行多参数拟合，其中上述5 个参数为共用参数，而应变率作为独立变量不参与共用，拟合得到的参数见表2。同时，本研究采用的拟合方法解决了参考文献［12］中不同应变率下ZWT 非线性粘弹性本构模型的参数值难以恒定，无法使用统一本构参数描述材料力学行为的问题。拟合得到的结果为多应变率共用，可以描述PBX 炸药在不同应变率情况下的力学行为。

表2 无损伤本构参数Table 2 Undamaged constitutive parameters

图6 为运用拟合参数的Z-W-T 本构模型曲线与试验得到的PBX 炸药本构曲线。经过误差分析，Z-W-T本构方程对PBX 炸药力学性能拟合的相关指数可达0.95 以上。拟合参数可较好的表示未达到损伤前的PBX 炸药力学性能。

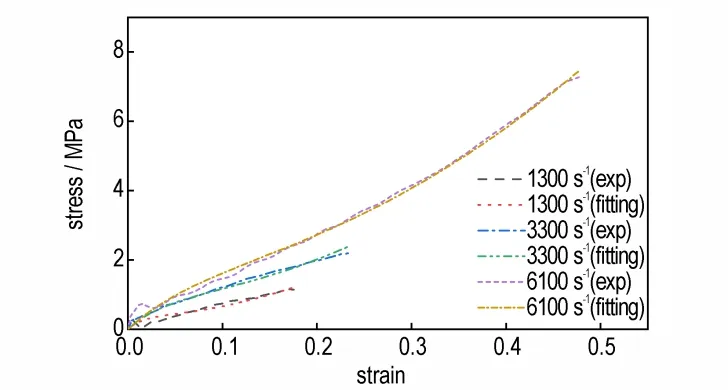
图6 拟合Z-W-T 本构曲线与试验本构曲线对比Fig.6 Comparison between fitting Z-W-T constitutive curves and experimental constitutive curves

其次，为了拟合损伤变量中的参数，将应变率在3300 s-1和6100 s-1条件下达到损伤的应变范围内的损伤应力σr与拟合得到的不含损伤的本构方程在相同应变范围内的无损应力σ相除，消除拟合方程中的自变量，得到式（9），并对其进行参数拟合：

D0初始损伤因子，根据所研究材料的真实条件测量评定得到，但目前对于PBX 炸药材料，该值的测量与评定方法不成熟，因此本研究通过限定施加合理取值范围进行拟合，得到损伤变量参数D0=0.2，δ=1.28031，b=1.01783。

拟合结果与实际结果的对比如图7 所示。由图7可见，拟合结果与实际结果较为吻合。

图7 本构损伤部分的拟合结果与试验结果对比Fig.7 The comparison between the fitting results of constitutive damage and the experimental results

最后，对如式（5）所示的Z-W-T 本构模型的损伤阈值与应变率相关关系，从试验得到的详细数据中，找到对应应变率条件下本构数据中出现损伤的数据点，即随应变增大对应应力开始减小的数据点，将该数据点的应变值作为损伤阈值。1300 s-1应变率对应的损伤阈值为0.18637；3300 s-1应变率对应的损伤阈值为0.29994；6100 s-1应变率对应的损伤阈值为0.62453；用以上三组数据对式（5）中的参数进行拟合，获得表示应变率与损伤阈值的关系，A=-0.12055，B=9.52536×10-5。

综上所述，对采用的Z-W-T 本构模型，所有的参数见表3。

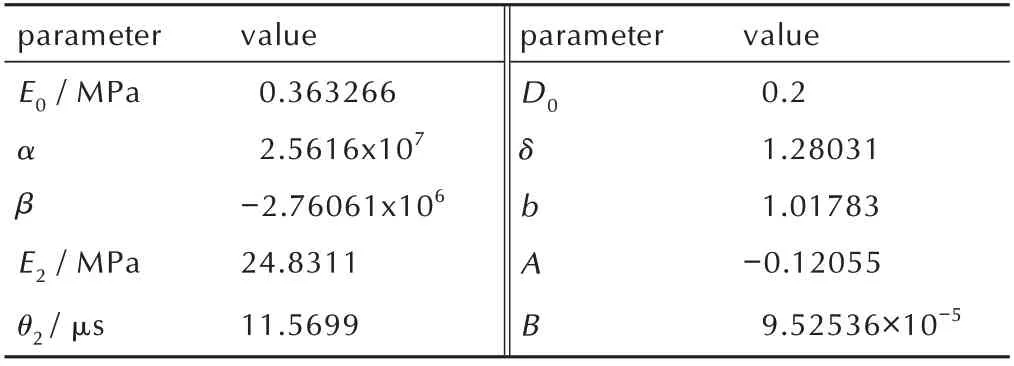
表3 带损伤Z-W-T 本构模型参数Table 3 Parameters of Z-W-T constitutive model with damage

4 数值仿真

4.1 含损伤变量的Z-W-T 本构材料子程序

获得合适的本构参数对PBX 材料的力学性能进行表征后，对其材料子程序进行编写。在大型商业有限元软件ABAQUS 中，为了满足多样化的本构模型需求，留有材料子程序的接口供使用者使用。本研究在高应变率条件下的PBX 炸药材料力学性能更符合非线性力学、瞬态响应分析的范畴与ABAQUS/Explicit模块的材料子程序VUMAT 的使用条件更为契合。根据VUMAT 材料子程序的开发逻辑，将带损伤变量的Z-W-T 本构模型从一维形式转变为三维增量形式是开发过程的重点和难点。

根据弹塑性力学，运用第二Poila-Kirchhoff 应力张量和Green 应变张量将式（6）变换为三维张量形式［13］：

式中，μ为泊松比。根据参考文献［14］和［15］对PBX炸药材料泊松比的描述可知，其泊松比与多种因素有关，不同情况下其值不同，本研究根据参考文献取值0.19。

将高频Maxwell 粘壶部分用Pij表示，当Δt足够小时，将t和t+ Δt时刻的Pij相减，可得到其在时间增量Δt内的增量式（12）：

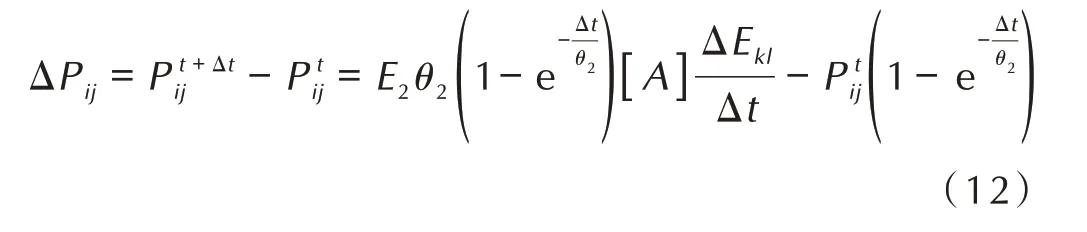
另外，对代表非线性弹性的部分直接进行差分，得到其在时间增量的增量形式：

结合式（12）和式（13），并且其中代表应力与应变的符号换为常用的符号，可得到不带损伤的Z-W-T 本构模型的三维张量增量形式：

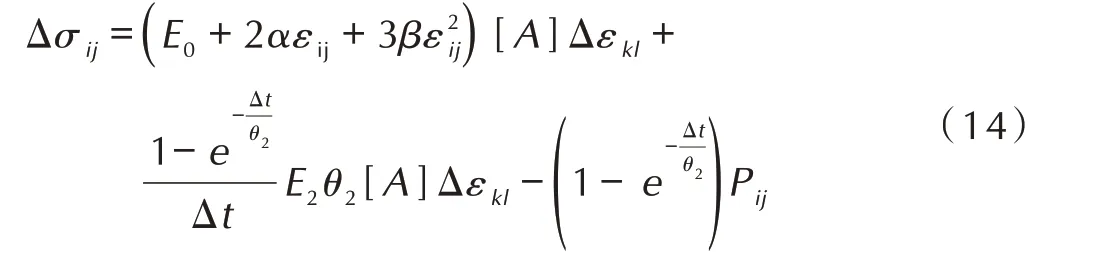
根据拟合出来的关系计算损伤阈值和损伤变量时，需要将三维张量形式的结果转换为等效形式进行计算。同时，本研究对损伤变量计算是假设其演化过程是各向同性的。等效应变的计算形式为：

根据式（5）计算应变阈值，当等效应变大于当前时间增量应变率对应的应变阈值时，运用式（16）计算损伤变量D的增量形式：

则t时刻的损伤变量为：

因此，损伤后的应力可按照式（18）计算：

严格按照ABAQUS/VUMAT 材料子程序的接口，按照以上逻辑完成材料子程序的编写。

4.2 材料子程序的验证

完成材料子程序的编写后，根据参考文献［16］中对二次开发材料本构模型的验证方法，验证其正确性。建立了图8 所示的模型，该模型是一个1 mm×1 mm×1 mm 的立方体，并且仅划分为一个单元，设置为C3D8R 单元类型，底面施加U2=UR1=UR3=0 的约束，即约束了y 方向的平移自由度、绕x 轴和z 轴的旋转自由度。为了便于控制应变量顶面施加指向底面的固定位移载荷，相当于对该单元进行了压缩受力仿真。可获得该单元的应力-应变曲线，并将其与实验结果进行对比。

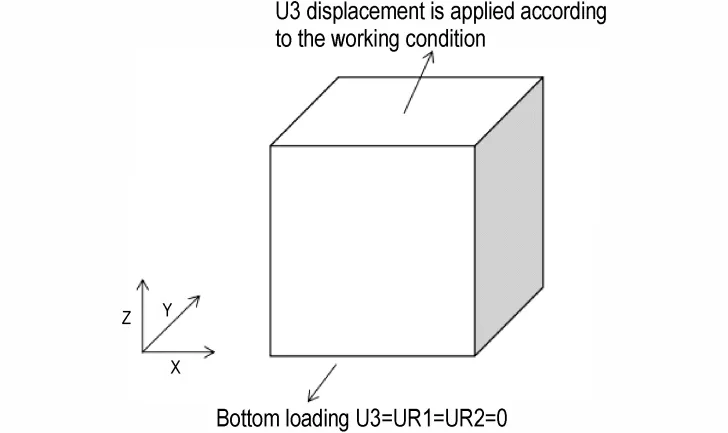
图8 验证子程序的计算模型Fig.8 Calculation model of verification subroutine

对模型进行的压缩工况仿真，并将其力学响应与试验结果进行对比。该仿真中通过定义不同大小的位移载荷控制应变量，通过定义相应的幅值时间控制应变率，由此进行不同应变率下的压缩工况仿真。仿真结果与试验结果的对比如图9 所示。从图9 可以看出，Z-W-T 本构材料子程序在仿真程序中对PBX 炸药力学性能的再现整体较为可靠，在低应变率与高应变率的损伤部分的误差会相对较大，总体结果良好。

图9 验证子程序的仿真结果与试验结果对比Fig.9 The comparison between the simulation results of the verification subroutine and the experimental results

4.3 带壳装药的破片撞击仿真

通过试验与材料子程序开发将PBX 炸药材料的含损伤力学性能嵌入到商业有限元软件后，对PBX 炸药材料进行典型冲击工况的仿真，分析其损伤演化。武器装备战斗部受到破片撞击是其在勤务过程中常见的意外情况，也是国内外学者研究的典型工况。目前大多数研究都集中在破片撞击作用下发生的燃烧、爆燃及爆轰等反应。而破片撞击导致的过度形变也会导致装备战斗部中的PBX 炸药材料产生微孔洞和微裂纹之类的损伤，对炸药的宏观力学性能、爆轰及安全性能产生影响。因此，利用本课题开发的材料子程序，进行带壳装药的破片撞击仿真，对损伤变量场进行分析。

实际情况中，破片多为不规则形状，由于成本、工作量的原因，根据参考文献［17］对物理模型进行简化，建立如图10 所示的物理模型。破片为典型的平顶圆柱，尺寸为Φ12 mm×20 mm，破片与壳体间有1 mm间隙；PBX 炸药尺寸为Φ70 mm×70 mm；战斗部壳体厚度采用飞鱼战斗部的壳体厚度为20 mm；为减少计算成本，进行四分之一建模。

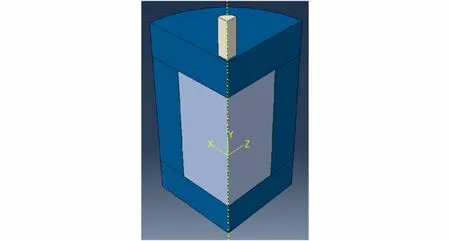
图10 带壳装药破片撞击仿真物理模型Fig.10 Simulation physical model of shell charge fragment impact

破片采用钢材料，战斗部壳体采用铝材料，用Johnson-cook 材料模型定义，破片和战斗部壳体的材料参数如表4 所示。

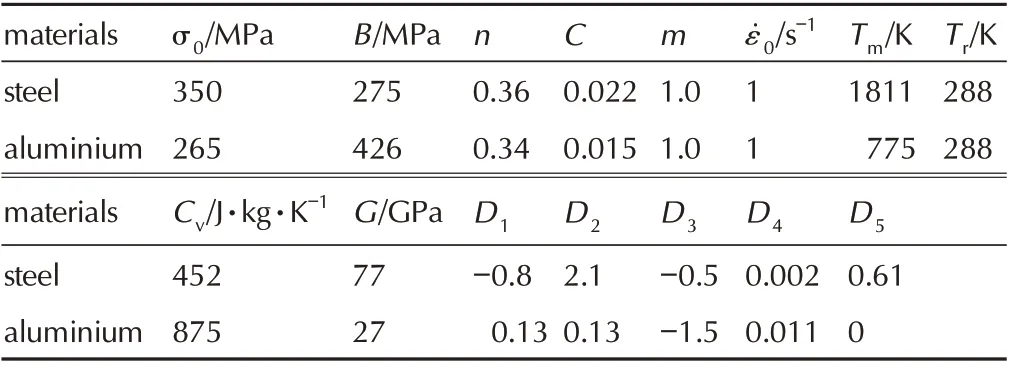
表4 钢和铝的Johnson-cook 材料模型参数［18Table4 Johnson-cook material model parameters of steel and aluminum

划分完网格的模型有55万个单元，根据参考文献［19］中的破片速度梯度，将破片分别赋予600，800，1000 m·s-1的速度，对这三个工况进行仿真。仿真结果如图11 所示。

从图11 可以看出，在破片撞击后，在与破片速度方向垂直的两个平面，由于外壳的形变与PBX 炸药的形变，这两个部位出现了较大的间隙。在冲击起爆的情况下，越大的装药间隙，越不容易形成爆轰反应，会残留越多的药量［20］，同时也会在一定程度内削弱爆轰波的强度［21］。从图13 战斗部装药损伤变量云图可以看出，PBX 炸药在直接遭受破片撞击的表面会出现较大范围的损伤，在直接撞击面的远端面的中心和边缘，也出现了损伤。对比图12 和图13，可以发现碰撞冲击产生的应力波经过传递及作用后，对比损伤变量值较高位置的应力与周围损伤变量值较低位置的应力，损伤值较高位置的应力值较小，说明损伤影响了材料承载能力。同时，600，800，1000 m·s-1工况的仿真输出结果表明：破片分别在80，84，90 μs 失去冲击力，发生回弹。结合图14 撞击侧单元D-t曲线中可以发现，直接遭受撞击部位并没有在一开始即出现损伤，而直接遭受撞击部位的边缘却在一开始出现了损伤。分析原因可能是直接撞击部位的应变率较大，损伤应变阈值较高在撞击瞬时并未达到其值；而撞击的边缘部位有一定大小的应变且应变率不大，因此在撞击后迅速出现了损伤。随着应力波在PBX 炸药材料中的作用，直接撞击部位的应变率降低后，应变并没有变小，则在直接撞击面就出现了大面积的损伤。

图11 带壳装药破片撞击仿真整体应力结果Fig.11 Simulation results of global stress of shell charging fragment impact

图12 带壳装药破片撞击仿真战斗部应力结果Fig.12 Simulation results of warhead stress of shell charging fragment impact

图13 战斗部装药损伤变量云图Fig.13 Damage variable cloud diagram of warhead charge

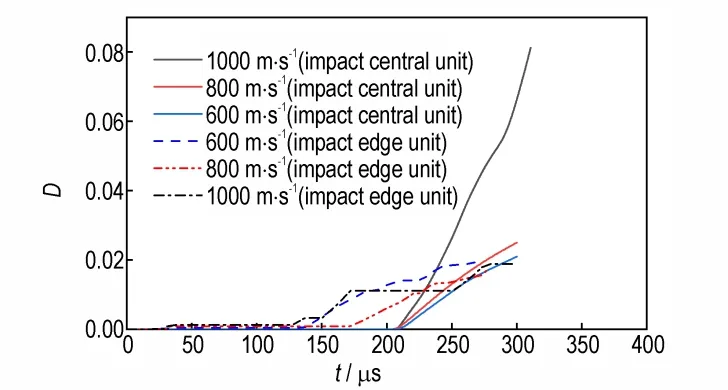
图14 各工况不同撞击部位单元D-t 曲线Fig.14 D-t curves of different impact positions under different working conditions

PBX 炸药带壳装药破片撞击变形图和PBX 炸药损伤变量云图分别从宏观与微观两个角度，反映了带壳战斗部装药在破片撞击情况下可能出现的对其爆炸性能及安全性能产生影响的区域，可为相关学者研究PBX 炸药损伤特性与其装药结构改进提供依据。

5 结论

对PBX 炸药材料从SHPB 试验获取本构、本构模型表征、有限元软件材料子程序二次开发和带壳装药破片冲击仿真进行了带损伤的PBX 炸药材料模型的研究，得到以下结论：

（1）通过SHPB 试验获得了PBX 炸药具有应变率效应且达到损伤范围的本构数据，可真实反映PBX 炸药的力学性能。

（2）基于试验获得的PBX 炸药本构数据和带损伤的Z-W-T 本构模型，采用分段、分步拟合的方法，拟合出了误差极小的本构模型参数，可准确表征PBX 炸药的力学性能；并基于此完成了有限元软件ABAQUS 材料子程序VUMAT 的开发工作，经过仿真验证满足实际工程的精度要求。

（3）调用编写的材料子程序进行的带壳装药破片撞击仿真的仿真结果从宏观变形与微观损伤两方面，对可能出现间隙、损伤微孔洞微裂纹的地方进行了预测；同时仿真结果也表明，PBX 炸药材料并不是在撞击最剧烈的时刻出现损伤；损伤常出现在后续材料内的应力波传递过程中。相关仿真结果和材料子程序对后续研究者观测其损伤部位与改进其装药结构提供了依据与工具。