多约束装配线平衡问题的知识驱动系统控制启发式算法

郑巧仙，肖晖，李明

(1.湖北大学计算机与信息工程学院，湖北 武汉 430062;2.武汉科技大学理学院；湖北 武汉 430065)

0 引言

装配线是一种生产系统，经常用于大批量生产标准化产品.在装配线上，未完成产品通过连续的工位，不同的工位执行不同操作，最终获得完整的产品.装配线平衡问题[1](assembly line balancing problem, ALBP)可以描述为:给定一个存在优先关系的操作集合与工位集合，将各项操作唯一分配至其中某个工位，最小化各个工位时间的差异，并且各个工位时间不能超过装配线的生产节拍.ALBP在制造业和其他流水线生产行业有很高的实用价值，是调度优化中的一类重要问题，也是离散约束优化中的NP难问题[2].

研究初期，ALBP的约束条件主要为操作间的优先关系约束，其后基于企业实际需求，其他约束如并行约束[3]、资源约束[4]以及时间和空间约束[5]等被相继加入；随着企业装配环境的进一步复杂化，对装配线的要求更高，更多更复杂的约束同时被引入，新增加的约束主要为位置约束、同步约束、消极区域约束等[6-7]，相应ALBP称为多约束装配线平衡问题(multiple constraints assembly line balancing problem, MCALBP).

作为离散约束优化问题[8-9]，MCALBP具有约束条件多、可行解空间离散以及可行解少等特点，求解的难度较大，问题是否存在可行解也难以确定，所以在求解前如果能够准确判定可行解的存在性，有重要的实用价值.目前对离散多约束优化问题可行解的存在性方面的研究很少，郑巧仙等对这一问题进行了分析和证明[10].而在求解算法方面，主要有爬山算法[11]、殖民竞争算法[12]和教与学算法[13-15].上述算法大都采用罚函数法处理问题中的主要等式约束，然而由于是近似算法，理论上无法保证所得的解是最优解，从而难以保证所有的等式约束得到满足，即难以保证所得的解为MCALBP的可行解.

本文中针对企业的实际需求，提出一种含有更多约束的MCALBP，然后基于各约束自身的特征以及相互耦合关系等知识，设计一种能主动控制所有约束得到满足的系统控制启发式算法，求解问题的近优解.

1 多约束装配线平衡问题模型

1.1 问题描述设MCALBP的操作集合为I={i|i=1,2,…,|I|}，工位集合为J={j|j=1,2,…,|J|}，装配线的生产节拍为C.集合I中操作i的操作时间为ti.记P=(Pi2,i1)|I|×|I|为一个0-1矩阵，用以表示不同操作之间的直接优先关系，如果操作i1是操作i2的直接前序，Pi2,i1=1；其余情况下，Pi2,i1=0，i1,i2∈I.通过直接优先关系矩阵P可以得到优先关系矩阵Q，记之为Q=(Qi2,i1)|I|×|I|.MCALBP所研究问题除优先关系约束外，还要考虑下面三类约束：

1)加强边约束：该约束要求一些存在直接优先关系的成对操作分配至同一个工位，并且在完成其中一项操作后马上开始另一项操作.称满足加强边约束的成对操作统为加强边操作.设问题有N对加强边操作，其中第n对的第l(l=1,2)项操作记为JQl,n(n=1,2,…,N)；

2)位置约束：该约束要求一些操作必须分配至指定的工位，可以帮助企业减少运营成本.相应的工位称为强位置工位，相应的操作称为强位置操作.设问题有|K| 类位置约束，其中第k(k∈K，K={k|k=1,2,…,|K|})类强位置操作集合记为Qtk，强位置工位集合记为Qsk.

3)消极区域约束：该约束要求两个集合中的操作不能分配至同一个工位，称相应操作为互斥操作.记问题的互斥操作集合为Tam(m=1,2)，其中集合Ta1(第1类互斥操作，所分配的工位称为第1类互斥工位)中的操作和集合Ta2(第2类互斥操作，所分配的工位称为第2类互斥工位)中的操作间存在消极区域约束.

本文中所研究问题以最小化装配线的生产节拍为目标，除此之外还要考虑到企业希望将一些操作尽可能分配至某些工位的实际生产需求，增加了相应的目标，称之为弱位置目标.弱位置目标中相应工位称为弱位置工位，相应操作称为弱位置操作.设问题存在|K′|类弱位置目标要求，其中第k′(k′∈K′，K′={k′|k′=1,2,…,|K′|})类弱位置操作集合和工位集合分别记为Rtk′和Rsk′.于是得到问题的优化目标为：最小化装配线的生产节拍和不满足弱位置目标要求的操作项数，称该问题为第2类多约束装配线平衡问题(MCALBP-2).

1.2 数学模型设xij(i∈I,j∈J)为0-1变量，若操作i分配至工位j，则xij=1；否则，xij=0.该问题的数学模型如下：

(1)

xi1j=xi2 ji1=JQ1,n;i2=JQ2,n;j∈J;n=1,2，…,N

(2)

(3)

xi3j+xi4j≤1i3∈Ta1,i4∈Ta2

(4)

(5)

(6)

(7)

其中，(1)式为去量纲化处理后所得的问题的目标，(2)式为加强边约束，(3)式为位置约束，(4)式为消极区域约束；(5)～(7)式为装配线平衡问题的一般约束，依次为优先关系约束、节拍约束和操作的分配约束.

2 知识驱动的系统控制启发式算法

MCALBP有多类约束，这些约束之间相互耦合、相互制约.若问题存在可行解，则可在先验知识的基础之上，系统地考虑问题的特性和各类约束的特征，提出一个面向所有约束的整体控制策略，以此为基础，设计启发式算法主动控制满足各类要求，求解问题的可行解.

知识驱动的系统控制启发式算法先对数据预处理，整合加强边约束操作的信息，处理后的数据满足加强边约束，并创建一个信息矩阵用于对强、弱位置操作分配定位.再依次对各工位基于各类约束操作的分配要求根据其优先级别生成相应的候选操作集合，并用所设计的操作选择规则[16]选择操作；根据当前工位的已被分配时间与所设定生产节拍之间的关系所设计的操作分配规则[16]，将操作分配至工位，得到各工位的操作分配方案，求得问题的可行解.最后更新信息矩阵，进行下一次的遍历搜索.遍历搜索过程依据定界规则[16]减小工位时间的变化区间[Lbbest,Ubbest].算法的主要流程如图1所示.

图1 知识驱动的系统控制启发式算法流程图

2.1 加强边约束操作的信息整合在MCALBP中，加强边约束要求一些存在直接优先关系的成对操作分配至相同工位，并且在完成其中一项操作后马上开始另一项操作.为满足此要求，算法在数据预处理时将这些操作的原序号保留，将操作时间集中在一项操作上，同时重新定义相关的优先关系和操作的特殊属性.

记i1,i2,…,im之中含有多对加强边操作(操作(i1,i2),(i2,i3),…,(im-1,im)间存在加强边约束)，对这些操作进行信息整合：

Step1：找到这些操作中的最前序操作.根据加强边约束的定义，操作(i1,i2),(i2,i3),…,(im-1,im)间存在直接优先关系，则最前序操作为i1.

Step2：将所有操作的时间集中在最前序操作i1上，更新操作时间，令ti1=ti1+ti2+…+tim，ti2=ti3=…=tim=0.

Step3：更新操作间的优先关系.找到im′(m′=1,2,…,m)的直接后继操作集合DSim′和直接前序操作集合DPim′，令所有加强边约束操作的直接前序和直接后继为每项加强边操作的直接前序和直接后继，即令Pi,im′=1,Pim′,i′=1,∀i∈DSc,∀i′∈DPr，其中，DSc=DSi1∪…∪DSim，DPr=DPi1∪…∪DPim.然后更新优先关系矩阵Q.

Step4：更新操作的各类特殊属性.进行信息整合后，加强边约束操作i1,i2,…,im被视为一项操作.若其中某些操作有特殊要求，对其他操作也增加相同要求，即对它们依据位置约束(消极区域约束)、弱位置要求的优先级从高到低依次增加属性，以此保证i1,i2,…,im被分配至相同工位.例如，当操作i1,i2,…,im中存在某类强位置操作时，其他所有操作都增加该类强位置操作；当操作i1,i2,…,im中存在某类强位置操作和弱位置操作时，其他所有操作都增加该类强位置操作.

2.2 位置操作的信息矩阵MCALBP的位置约束要求强位置操作必须分配至与之对应的某些强位置工位.为了保证此约束得到满足，算法将强位置操作的所有前序操作时间平均分配至此强位置工位的前序工位，称该分配原则为平均分配原则.平均分配原则，首先确定强位置操作(记为i)的可分配强位置工位的最小与最大的序号，初步定位操作i可分配的工位；再将强位置操作i的前序操作时间平均分配至其最小可分配工位的各前序工位中，保证强位置操作i尽可能分配至其最小可分配工位.

算法中的定界规则[16]设定了工位时间的上界，即装配线的生产节拍.当生产节拍较大时，平均分配原则很容易控制操作分配满足位置约束；但当生产节拍较小时，若强位置操作i的前序操作时间长度较大，平均分配原则可能无法保证在最大可分配工位到达之前将其分配完毕，于是此操作及其至少一项前序操作必须分配至最大可分配工位，在此情况下，如果这其中某项前序和操作i有互斥关系，算法就得不到可行解.

(10)

2.3 候选操作集合在MCALBP中，生成候选操作集合不仅只取决于优先关系，还需要考虑目前工位的强、弱位置属性和操作的强、弱位置属性，以及操作间的互斥属性.若工位j不是强位置工位，候选操作集合CA不能含有强位置操作；若工位j不是第k类强位置工位时，CA中不能含有第k类强位置操作，弱位置操作也有类似要求但不强制；若工位j中含有属于Ta1中的操作时，CA中不能含有属于Ta2中的操作；若工位j中含有属于Ta2中的操作时，CA中不能含有属于Ta1中的操作.候选操作集合的生成步骤如下：

Step1：基于优先关系，生成工位j的候选操作集合CA[16].

Step2：基于工位的强位置属性，更新CA.

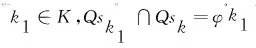
Step3：基于工位上操作间的互斥属性，更新CA.

1)若工位不存在Ta1或Ta2中操作时，保持CA不变.

2)若工位有只属于Ta1中的操作，为防止分配Ta2中与之相互斥的操作，更新CA为CA-Ta2.

3)若工位有只属于Ta2中的操作，为防止分配Ta1中与之相互斥的操作，更新CA为CA-Ta1.

Step4：基于工位的弱位置属性，更新CA.

若经过Step2和Step3，更新后CA为空集，那么表示有约束未得到满足，算法结束.

(11)

即已分配的工位平均前序时间长度大于等于理论的可分配工位平均前序时间长度，称操作i的已分配前序满足平均分配原则，其中已分配操作的集合为V.同理可定义分配弱位置操作的前序需满足的平均分配原则.

算法基于操作的属性为当前工位选择操作，设置各属性操作的选择优先级从高至低如下：

ⅰ)以当前工位为最大可分配工位的强位置操作及其前序操作；

ⅱ)以当前工位为最大可分配工位的弱位置操作及其前序操作；

ⅲ)可被分配至当前工位的强位置操作和弱位置操作、没有满足平均分配原则的强位置操作的前序操作；

ⅳ)没有满足平均分配原则的弱位置操作的前序操作；

ⅴ)其余强、弱位置操作的前序操作；

ⅵ)其余候选操作.

若在候选操作集合中，属于同一优先级的候选操作有多项，算法将从以下操作选择规则中选择合适的规则选择操作.

1)操作选择规则1：根据候选操作i的操作时间及其所有未分配后继的操作时间之和，即位阶权重[16]，选择其中权值最大的一项操作.

2)操作选择规则2：根据候选操作i的操作时间及其对未分配强、弱位置操作的贡献值大小Wi选择其中权值最大的一项操作.Wi可由式(12)计算得到，其中UV为未分配操作的集合.

式(12)中，若操作i是更多未分配强和弱位置操作的前序，并且这些强、弱位置操作的最小可分配工位序号越小，则表示操作i对分配强、弱位置操作的贡献值越大，所以应优先选择该操作.

3)操作选择规则3：若当前工位确定含有某类互斥操作，为尽可能将同一类互斥操作分配至此工位，在已有选择权值的基础上成倍增加候选操作中该类互斥操作的选择权值，然后再选择权值最大的操作.

操作选择规则仅为当前工位选择操作，决定所选择操作是否分配的是操作分配规则.操作选择规则的具体步骤如下：

(13)

否则，搜索操作i1在CA中的所有前序操作(记为i3)，根据式(14)更新CA，优先选择这些操作.

(14)

然后基于位阶权重计算各候选操作的选择权值，并进入Step7；若CA中不存在上述前序操作，进入Step2.

(15)

(16)

然后基于位阶权重计算各候选操作的选择权值，并进入Step7；若CA中不存在上述前序操作，则进入Step3.

Step3：若候选操作集合CA中存在可分配至当前工位的强位置操作(记集合为CA1)、弱位置操作(记集合为CA2)和未满足工位平均分配原则的强位置操作的前序操作(记集合为CA3)，更新CA为：CA1∪CA2∪CA3，其中：

集合CA中的所有操作(记为i).若i∈CA1或CA2，则根据位阶权重分别计算其选择权值；若i∈CA3，根据式(12)计算其选择权值，并进入Step7；若集合CA中不存在上述操作，进入Step4.

Step4：若候选操作集合CA中存在未满足工位平均分配要求的弱位置操作的前序操作，按式(20)更新CA，然后根据式(12)计算各候选操作的选择权值，并进入Step7；若CA中不存在上述操作，进入Step5.

(20)

Step5：若候选操作集合CA中存在强、弱位置操作的前序操作，根据式(21)式更新CA，然后根据式(12)计算各候选操作的选择权值，并进入Step7；若CA中不存在上述操作，进入Step6.

(21)

Step6：根据位阶权重计算集合CA中各候选操作的选择权值，并进入Step7.

Step7：根据操作选择规则3更新各候选操作的选择权值，并选择操作，结束操作选择.

2.5 信息更新若算法为工位j分配一项操作i后，除了更新工位时间、解、已分配操作集合等信息，还需更新以下所列举情形相对应的信息：若操作i属于Ta1(或Ta2)，更新工位相应的互斥属性；若操作i属于加强边约束操作，搜索与操作i进行整合的其他加强边约束操作，并将这些操作都分配至当前工位.

3 算例

表1～表3为某实际MCALBP的测试数据，其中表1为147项操作的操作时间，表2列出了操作间的192个直接优先关系(表中有序数对(i1,i2)表示操作i1为操作i2的直接前序)，表3给出了有特殊要求的所有操作及其相应要求，共含有7类强位置操作，8类弱位置操作，两类互斥操作和21对加强边约束操作，并设定装配线的工位个数为14.

表1 操作时间 s

表2 操作间的直接优先关系

表3 特殊操作及其要求

利用所提的启发式算法对上述多约束问题进行求解，求解的结果见表4，所得的操作分配方案见图2.实验(包括后续实验)在配置为CPU：Intel(R) Core(TM) i5-3337U@1.80 GHz，内存：4.00 G的计算机上基于Python软件完成，算法中参数的取值为5，最大迭代次数NC=100.

表4 对实际算例的求解结果

图2 实验算例的操作方案分配图纵坐标表示工位，横坐标为工位时间；标识表示强位置操作，表示弱位置操作(含第一类互斥操作)，表示第二类互斥操作(当此操作同时为强位置操作时，标识为)，表示其他操作，标识上方的数字为分配至该工位的操作序号，各工位最后的数值为此工位的工位时间.

比较图2的操作分配方案和表3的操作要求易知问题的所有约束，即位置约束、加强边约束和消极区域约束都得到满足，而8类弱位置要求也全部满足.算法所得的最小节拍为111，较算例的理论节拍仅大2，平衡率为97.55%，而计算时间不到5 s，都满足实际需求.

为进一步验证算法的有效性，将所提算法对目前已有的6个大规模标杆算例[17](相关信息见表5第1～4列)进行求解.表5中第4列为利用精确算法求解对应ALBP-2所得的最优节拍，第5～9列依次为所提算法求得MCALBP-2的节拍、所得解中未满足约束的个数和未满足弱位置要求的个数、所得解对应的装配线的平衡率以及算法的求解时间(秒).

表5 对标杆算例的求解结果

由表5的求解结果可知，对6个标杆算例，所提算法求得了所有算例的较优可行解，而对所有160个弱位置要求仅1个(算例Mukherjee中的弱位置操作83)没有满足，满足率为99.38%.所得解的平衡率均在90%以上，计算时间都不足10秒，满足实际需求.这说明所提启发式算法可快速、有效地求解MCALBP-2的近优解.

4 结论

本研究针对含有多类约束，在装配线运作过程中普遍存在的第2类多约束装配线平衡问题，提出了一种知识驱动的系统控制启发式算法，解决了多约束离散优化问题中一直存在的难以求得可行解的难题.与已有此类问题的求解算法相比，所提算法基于各类约束的特征以及它们之间相互耦合的关系等知识，系统设计，整体主动控制各类约束得到满足.由于目前多约束单边装配线平衡问题的研究还处于初步阶段，相关数据缺少，所以只用了6个含有多约束的标杆算例.接下来将对单边装配线平衡问题的标杆算例进行改造，增加文章所说的多种约束，得到更多的单边多约束问题的算例数据.