燃气轮机进气过滤系统维修周期经济性分析

金云峰，刘超*，邓高峰，关运龙，郝建刚，黄海舟，蒋东翔

（1. 清华大学能源与动力工程系，北京市 海淀区 100084；2. 建筑安全与环境国家重点实验室，北京市 朝阳区 100013；3. 华电电力科学研究院有限公司，浙江省 杭州市 310030）

0 引言

为保证进入重型燃气轮机内的空气品质，进气过滤系统通常被安装在燃气轮机压气机进口处，通过粗滤和精滤两级过滤，实现对空气中沙尘、盐雾、细小颗粒物等杂质的过滤和去除[1]。但是，进气过滤系统并不能完全吸附空气中的污染物，特别是随着进气过滤系统使用时间的累积，过滤效率发生退化，可能导致少量杂质进入燃气轮机流道内，引起叶片磨蚀、腐蚀、积垢、堵塞等多种类型的气路故障，导致燃气轮机输出功率与热效率下降[2-6]。研究表明，即使少量的杂质进入燃气轮机流道内，经过累积也会造成燃机出力下降与热耗率的提升。

进气品质引起的燃气轮机退化和故障问题中，发生频率最高、对性能影响最明显的是压气机积垢。有研究表明压气机积垢造成的性能损失占总损失的70%～85%[7]。因此压气机积垢造成的性能损失，也被当作是过滤系统效率下降带来的经济性下降和效益损失，是进气过滤系统维修经济效益中的重要考虑因素。

另外，进气过滤系统清除进气杂质的同时，进气系统引入了额外的空气阻力，导致压气机进口压力下降。由布雷顿循环的热力循环图可知，进气压力下降会导致输出功率的降低。研究表明，燃气轮机进气压力下降1 kPa，可导致输出功率降低1.42%[8]。压气机进口压力下降引起的燃气轮机经济性下降和效益损失，是过滤系统优化维修周期的考量因素之一。

为避免上述因素引起的损失，及时清洗及更换过滤系统部件可以有效保证燃气轮机进气质量、提高燃气轮机进口压力，对于燃气轮机运行的可靠性和经济性(热效率)有利。但不得不考虑的是，清洗和更换过滤系统部件会导致设备运维成本的增加(包括过滤系统部件更换成本、停机成本等)。因此，清洗和更换过滤系统部件的周期取决于上述几个方面的因素，各个因素之间相互影响、相互制约。为此，如何优化燃气轮机进气过滤系统的维护周期、提高进气过滤系统的运行经济性、降低运行维护成本、提高燃气轮机可靠性和经济性，受到了越来越多的重视[1,9-10]。

本文提出一种燃气轮机进气过滤系统维修经济效益分析模型，将总维修成本分解为初始成本、停机成本与性能下降成本3 部分；基于模型提出过滤器更换与压气机水洗维修周期的优化方式；最后，探究进气过滤系统异常退化条件下维修策略的调整方式。研究结果对于制定进气过滤系统维修策略、提高燃气轮机运行经济效益具有实用价值。

1 进气过滤系统经济效益分析模型

1.1 进气过滤系统构成

燃气轮机进气过滤系统一般包含：防风雨罩、过滤网、除水装置、预过滤器与高效过滤器等，其安装结构如图1 所示。本文所考虑的燃气轮机模型主要针对F级燃气轮机，其过滤器通常采用粗滤和精滤两级过滤。由于过滤器布置受到当地气候环境、污染程度等因素直接影响，不同地域和环境条件的燃气轮机进气过滤系统的配置不同，过滤器的寿命也有较大差别。为了便于对比分析，本文主要考虑同一地域燃气轮机维修策略优化前后的变化规律。在将来考虑不同地域的燃气轮机进气过滤系统维修策略时，通过对维修周期、维修成本等参数进行调整，即可获得相应的优化分析模型。

图1 燃气轮机进气过滤系统部件构成Fig.1 Components of gas turbine inlet filtration system

1.2 总体成本构成

燃气轮机及进气过滤系统年维修成本定义为Ctotal，其中包括了进气过滤系统维修所带来的直接成本(初始成本Cinit和停机维修成本Cdown)、进气过滤系统造成的燃气轮机性能下降带来的间接成本Cdeg。因此，Ctotal计算公式为

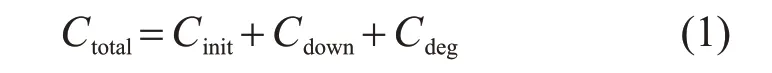
式(1)的构成基于以下简化假设：

1）忽略资金的时间价值。过滤器的维修周期在数千小时至上万小时，在严格的成本会计下需要考虑资金时间价值的影响；

2）除停机时间外，机组恒功率运行，且不考虑环境因素变工况的影响；

3）进气污染仅导致压气机积垢，未考虑其他气路故障(如透平热腐蚀等)对燃气轮机性能下降的影响；

4）压气机不进行在线水洗，且离线清洗可完全恢复燃气轮机性能；

5）不考虑严重故障(如叶片断裂)可能造成的成本。

1.3 初始成本

初始成本主要包括新更换过滤器的购买、运输、安装等成本，计算公式为

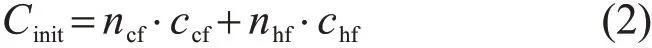
式中：ccf与chf分别为单组粗滤与精滤的初始成本；ncf与nhf分别为年更换粗滤与精滤的数量，由更换周期决定。

式中：tgen为燃气轮机年运行时间；tcf与thf为粗滤与精滤的更换周期。

1.4 停机成本

在燃气轮机进行更换过滤器、离线水洗压气机等维修时，需停机进行相关操作。维修所需的原材料、燃料等消耗以及停机导致的输出功率损失构成了停机维修成本。计算公式为

现实中单次停机可能同时进行多个维护操作，且对昼启夜停的调峰机组而言无需额外停机，在夜间即可完成维护。因此ndown有一定的优化空间，但在模型中进行了简单加和处理。

cdown的计算公式为

式中：Ngen为机组额定输出功率；tdown为单次停机时长；Wstart为启动过程折合耗电量；ce与cfuel分别为单位上网电价与度电气耗成本。

1.5 性能下降成本

由于压气机积垢导致燃机性能下降，如燃机出力减少、燃气耗率增加，因此带来性能下降成本。由于模型中假设燃气轮机恒功率输出，因此只考虑燃气消耗量相较于额定工况增加部分的成本。其计算公式为

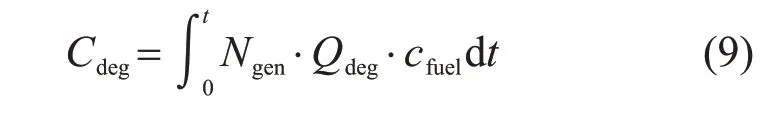
式中：Qdeg为由于性能下降导致的单位电量气耗率增加，其为运行时间t的函数，即Qdeg=Qdeg(t)。进一步地，可以将Qdeg(t)分解为3类退化因子的加和，表达式为

式中：Qfoul、QDPcf、QDPhf分别为压气机积垢、粗滤压差退化与精滤压差退化导致的燃气耗率增加。3 类退化因子均可以通过退化曲线求解定积分的方式，计算其所造成的性能下降成本。

在实际工程应用中，因压气机积垢、压差退化等因素导致的燃气耗率增加随时间变化的曲线应结合燃气轮机历史运行数据确定。本文中为简化模型，假设每类退化因子在对应的2 次维护操作期间，均随运行时间线性增长。因此，可确定公式(10)的具体表达形式为

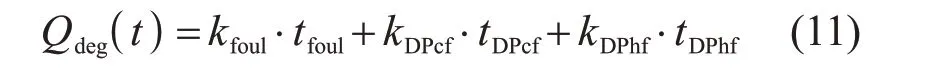
式中：kfoul、kDPcf、kDPhf为退化因子增长率；tfoul为t时刻距离上一次压气机水洗操作后的运行时间；tDPcf与tDPhf分别为t时刻距离上一次更换粗滤或精滤后的运行时间。

2 进气过滤系统维修周期优化

2.1 参数选取

由维修成本的构成可知，维修成本主要受粗滤维修周期、精滤维修周期、水洗周期3 方面影响。当粗滤维修周期、精滤维修周期、水洗周期延长时，维修成本降低，但性能下降带来的成本会显著提高。当上述3个维修周期缩短时，维修带来的初始成本与停机成本增大，性能下降带来的成本会显著降低。于是，整体维修成本优化需综合判断粗滤维修周期、精滤维修周期、水洗周期。

为此，本文选取3类维修周期作为决策变量，燃气轮机及进气过滤系统维修成本为目标函数，最大限度地降低维修成本。为便于对比分析，其余参数取为定值或遵循固定的函数变化规律[11-12]，如表1所示。

表1 维修成本计算参数选取Tab.1 Selection of maintenance cost calculation parameters

初始维修周期选取为tcf=2 200 h，thf=8 000 h，twash=2 000 h。经计算可知，优化前的年维修总成本为4 176万元。以此作为参照值，采用Python语言基于2.1节的成本计算方式，获得不同条件下的维修成本，并从压气机水洗周期优化、过滤器更换周期优化、维修成本优化前后变化3个方面进行分析。

2.2 压气机水洗周期优化

保持过滤器维修周期不变，改变压气机水洗周期，可以获得维修成本随压气机水洗周期的变化关系，如图2所示。

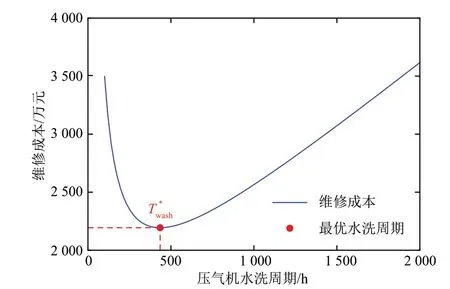
图2 压气机水洗周期与维修成本优化Fig.2 Compressor washing cycle and maintenance cost optimization

从图2 中可以看到，随着水洗周期的增加，维修成本先降低后增加，并存在最小极值点T*wash。由维修成本的构成可知，当水洗周期过短时，燃气轮机频繁停机造成的停机成本与水洗成本会迅速增加，导致维修成本的快速上升。而当水洗周期过长时，压气机长期运行在积垢状态下，燃气轮机的热效率较额定值明显下降，造成性能下降成本的升高。因此，在最优水洗周期下，即Twash=Tw*ash=467 h 时，各个子成本之间达到最佳平衡，从而实现维修成本的优化。可以看到，相比于原始2 500 h 的水洗时间间隔，随着水洗频率的增加，年维修成本存在约44%的优化空间。同时也应该注意到，最佳水洗周期的确定还与其他影响因素有关，如压气机性能对积垢的敏感程度、当地的污染水平、过滤器的精度等。

2.3 过滤器更换周期优化

与水洗周期优化类似，通过先后调整精滤与粗滤的更换周期，同样可以实现维修成本的降低。其变化关系如图3所示。

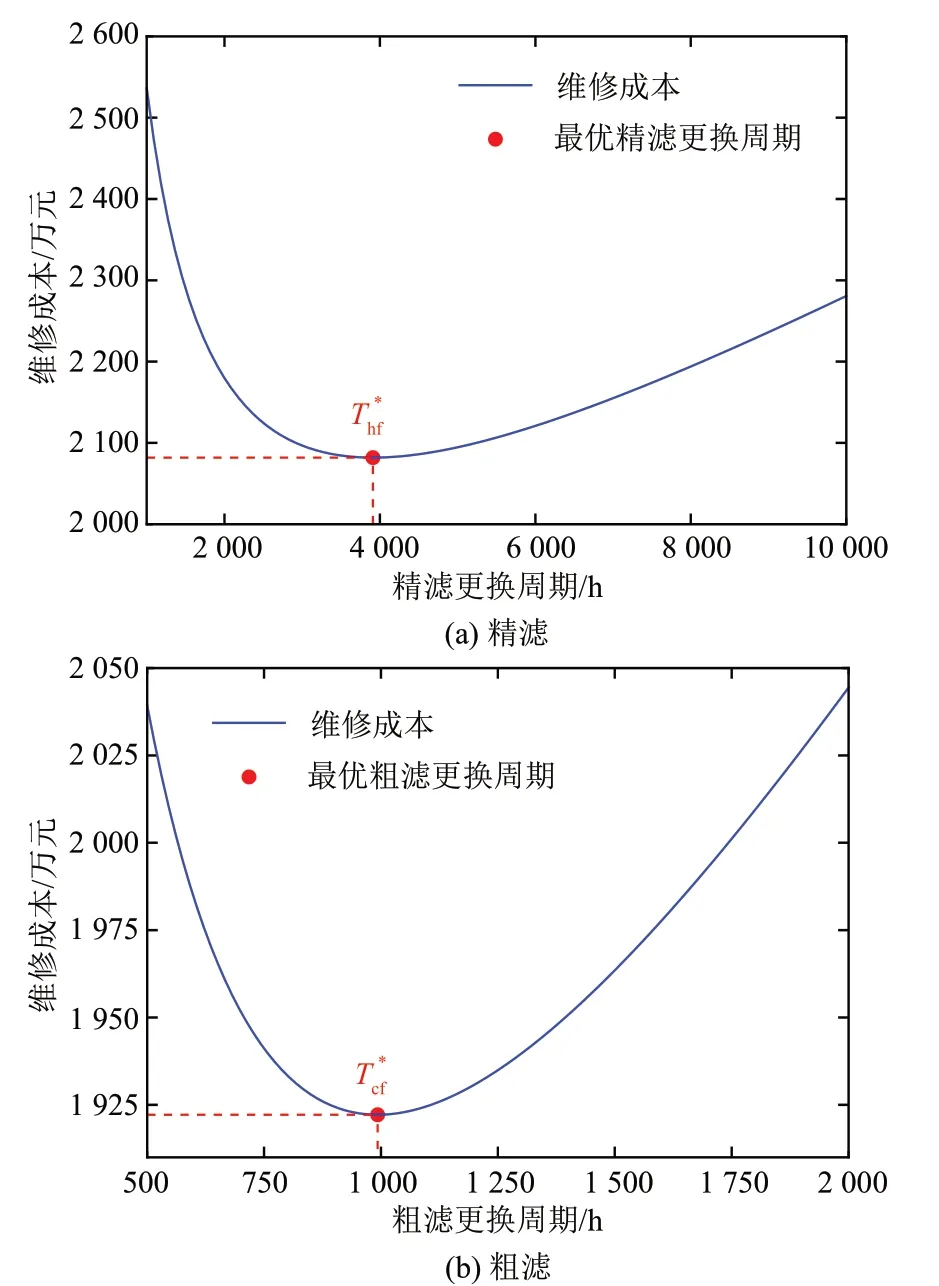
图3 过滤器更换周期与维修成本优化Fig.3 Filter replacement cycle and maintenance cost optimization

从图3 可以看出，过滤器更换周期优化与水洗周期优化规律基本一致，均存在着最优的极值点。但精滤与粗滤之间变化规律略有不同：精滤极值点右侧的曲线升高速率较为平缓，而粗滤右半部分的升高更为迅速。这表明延长精滤的更换周期对维修成本的影响并不十分显著，这是由于粗滤容纳了大部分的杂质，使得粗滤压差较精滤压差增长快约3.5倍，二者的时间尺度有明显差异。考虑到精滤初始成本远高于粗滤初始成本，这也是目前重型燃气轮机机组往往采用二级乃至三级过滤的原因。

2.4 维修成本优化前后比较

通过调整三类维修周期，完成了维修成本的优化，优化前后的对比如表2所示。

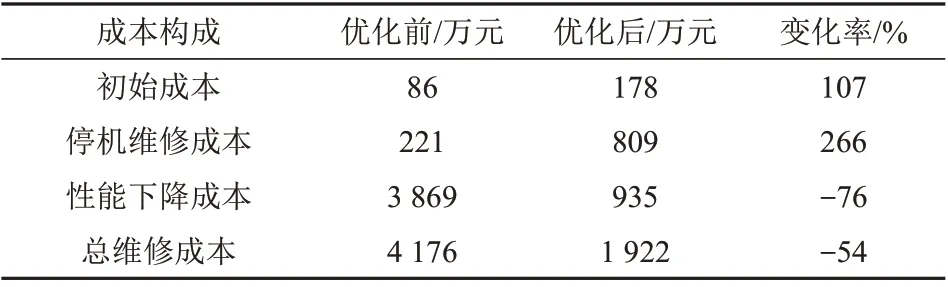
表2 优化前后维修成本对比Tab.2 Comparison of maintenance cost before and after optimization

从表2 可以看出，在优化前，性能下降成本占据了绝大部分的维修成本。而在缩短各个维修周期之后，尽管导致了初始成本和停机维修成本的上升，但性能下降成本显著减小。因此综合来看，通过调整过滤器更换与压气机水洗的维护周期，整体维修成本存在较大的优化空间。

3 进气过滤系统异常退化对最优维修周期的影响

前文讨论了通过选取维修周期实现整体维修成本的最小化，但是在燃气轮机机组实际工作过程中，往往因恶劣环境条件或异物撞击等，导致进气过滤系统出现异常退化，体现为过滤效率的大幅降低等。在这类情形下，维修策略也必须进行相应调整。

当过滤效率存在异常退化时，会造成压气机积垢速率的提升，相应地会使压气机等熵效率更快地下降到阈值下限，即剩余使用寿命下降。过滤效率异常退化下的最优压气机水洗周期如图4所示，其中，当DETAF=0时，代表过滤器处于正常状态，压气机积垢速率与表1 中数值保持一致。当DETAF=1时，过滤器发生密封泄漏，导致压气机积垢速率为正常值的2.5倍。DETAF在0～1时，假设压气机积垢速率为线性变化。

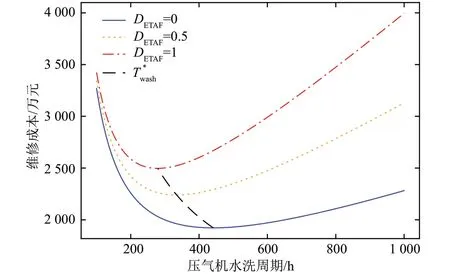
图4 过滤效率异常退化下的最优压气机水洗周期Fig.4 Optimal compressor washing cycle under abnormal filtration efficiency degradation

图4中，蓝色实线与标准状态下的维修成本曲线变化相同，而橘黄色与红色的点状线则代表不同程度的过滤效率异常退化。可以看到，随着异常程度的升高(即过滤器的局部泄漏面积增大)，曲线整体向左上方移动。将各状态点下的最优压气机水洗周期连接，如图4中的黑色虚线所示，表现为斜向左上方的一条曲线。这表明维修成本整体逐渐升高，对应的最佳压气机水洗周期缩短。

在过滤效率异常退化条件下，压气机水洗周期策略的调整方式与直观认识相一致，即当过滤效率低于正常值时，应当更为频繁地清洗压气机，且维修成本较正常过滤器更高。另外，从曲线图的左侧可以发现，当水洗周期减小时，不同DETAF对应的维修成本基本一致。这表明尽管过滤效率有所恶化，但通过频繁水洗压气机叶片，使压气机保持健康工作状态，燃气轮机运行期间即不会受到退化因素的影响，故性能下降成本趋于一致。但相应地，该类维修方式会造成初始成本与停机维修成本的显著上升。

4 结论

燃气轮机进气过滤系统和燃气轮机本体是相互联系的整体，部件之间相互耦合，在分析进气系统维修周期时，同样需要考虑燃气轮机本身退化规律的影响。为此，在已有监测系统的参数范围内，构建进气系统与燃气轮机的联合模型，分析不同部件退化过程，并进行实时识别和判断，从而用于进气系统维修周期的优化中。

1）通过选取粗滤维修周期、精滤维修周期、压气机水洗周期3类因素作为决策变量，以燃气轮机进气过滤系统维修成本为目标函数，实现了整体维修成本的最小优化。研究中发现，通过合理调整维修周期，因性能下降导致的成本显著减小，能够覆盖初始成本和停机维修成本的上升，从而优化总维修成本。

2）通过研究过滤效率异常退化情形下维修周期的调整策略，发现当存在过滤器密封泄漏等异常工作状态时，适当地加快部件的维修频率，可以减少该类异常条件造成的额外经济损失。

需要说明的是，针对燃气轮机进气过滤系统维修决策的分析引入了较多假设，其目的是使决策变量与目标函数之间的关系变化更直观清晰。下一步工作中将针对实际情况，结合燃气轮机实际运行的历史数据和检修记录，考虑变工况影响等因素，使分析结果更贴近实际。