阻尼对空爆荷载等效静载动力系数的影响*

耿少波，罗 干，陈佳龙，赵 洲

（中北大学土木工程学科部，山西 太原 030051）

易爆物品储存运输不当、燃气爆炸及暴恐袭击等时有发生，建筑结构在其服役期内遭受空爆荷载的概率逐渐增大。在进行结构抗爆分析时，抗爆设计规范普遍推荐采用无阻尼结构动力学体系，实现基于动力系数的等效静载抗爆分析。空爆荷载作用时长很短，可近似简化为三角形衰减荷载，这种简化可使不熟悉空爆荷载的结构设计人员完成抗爆计算。目前，民用建筑抗爆设计采用延性比等参数完成弹塑性抗爆分析，延性比为结构振动弹塑性变形最大值与弹性变形最大值的比。无阻尼自由振动体系没有能量耗散，是一种无休止的简谐振动。忽略阻尼作用，将放大结构振动各个阶段的位移幅值，而对延性比、动力系数等防爆设计参数的影响，还没有明确的理论结论。

认识到阻尼对结构振动响应存在影响，已开展了一些研究。在理论方面：Biggs采用等效单自由度（single degree of freedom, SDOF）进行抗爆分析时，提及阻尼对塑性阶段结构振动存在一定影响；Gantes 等分析空爆作用结构弹塑性振动时，指出阻尼对结构响应前几个振动周期存在一些影响；Riedel 等认为对于空爆作用下结构失效的情况，阻尼可忽略不计；方秦等建立并求解了端部有阻尼支承的梁体空爆作用下的振动方程，表明空爆荷载作用时长越短，端部的阻尼支撑对梁体的抗力提高作用越显著；郭东等采用杜哈梅积分方法，求解了空爆作用下弹性阶段含阻尼体系的等效单自由度动力方程，表明阻尼对反弹阶段的弹性位移振动影响显著，建议按30%进行位移折减，但未解决阻尼参数对塑性阶段响应的影响；陈万祥等求解了含阻尼的柔性边界支承下浅梁的振动方程，认为边界阻尼对结构的破坏模式不会发生变化；董彬等通过数值方法分析了含阻尼体系的梁体振动，表明加设阻尼器能有效控制空爆作用下的动力响应；杜志鹏等将船体结构简化为梁模型，分析了水下爆炸船体鞭状运动的阻尼效应，结果表明不考虑阻尼效应将高估运动响应幅值。由空爆作用结构试验可知，阻尼对冲击波荷载结束后的自由振动阶段确实存在影响：Liu 等分析了尺寸0.15 m×0.15 m×1.7 m 的钢筋混凝土梁在近场空爆作用下的破坏特征，实测位移显示，阻尼影响下结构在4～5 个振动周期后静止；Nassr 等完成了5 组工字型钢梁在远场空爆下的动力响应，4～6 个振动周期后结构静止；Zhang 等完成了50 kg炸药近场空爆作用下长2.5 m 钢管混凝土梁构件的振动效应，结果显示3～7 个振动周期后构件静止；Liu 等进行了尺寸0.22 m×0.3 m×2 m 的钢筋-玻璃纤维-混凝土梁构件在0.3～4 kg 当量炸药下近场空爆试验，发现梁体弹性振动、塑性振动、截面断裂3 种响应类型均在2～4 个振动周期后静止，塑性振动及截面断裂对应的阻尼明显偏大；Nagata 等、Syed 等、Ritchie 等、Shi 等和Foglar 等完成的结构空爆试验也充分说明阻尼对结构振动的显著影响。阻尼对空爆作用结构弹性阶段和塑性阶段强迫振动的影响、影响动力系数的程度、进而对抗爆设计的影响，试验上无法直接判别，也缺乏理论上的研究探索。

本文中，建立含阻尼的等效自由度体系振动模型，考虑空爆荷载作用时长与结构进入塑性振动时长的关系，将结构分为柔性结构、刚性结构、临界结构等3 种类型，进行各种类型下结构弹塑性振动方程的求解，结合延性比、动力系数等抗爆设计参数定义，以典型的阻尼比设计验算工况，对比现行抗爆设计规范的推荐公式，考查阻尼对动力系数的影响。

1 柔性结构空爆作用动力响应求解

1.1 弹塑性阶段动力方程

采用延性比的概念进行梁式及单向板结构空爆作用动力分析，且结构响应以弯曲振动分析为主时，等效单自由度方法具有良好的计算精度、简易的计算流程，被广泛采用，如图1 所示。

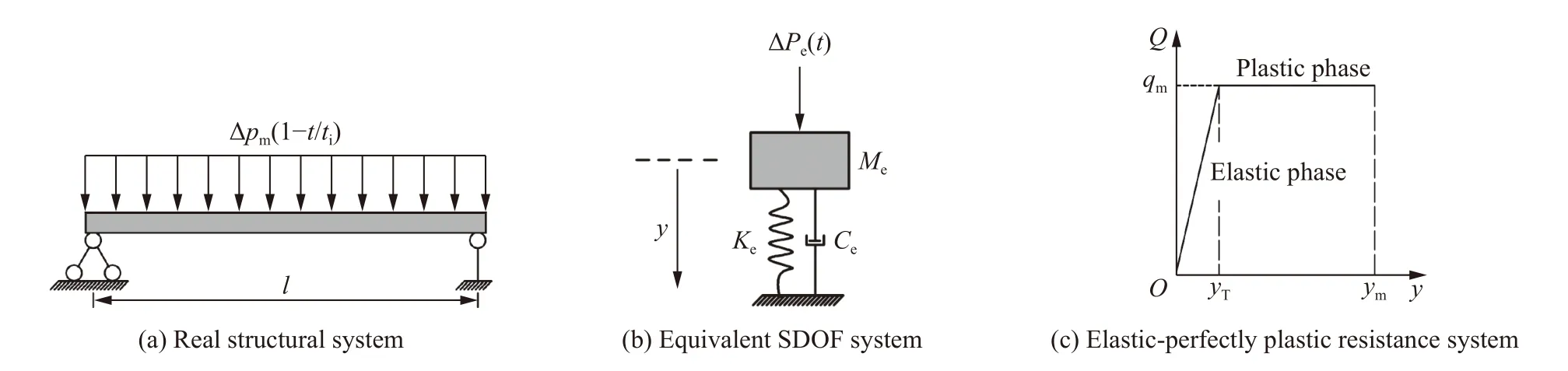
图1 理想弹塑性的含阻尼等效单自由度体系Fig. 1 Elastic-perfectly plastic SDOF vibration system with damping

考虑阻尼参数的弹性阶段等效单自由度振动方程为：

式中：为弹性阶段等效结构质量，为弹性阶段等效结构阻尼，为等效结构刚度，为与等效结构相等的、真实结构在典型位置处的振动位移，Δ()为等效结构承受的随时间变化的等效空爆荷载。各等效系数分别为：

式中：为结构每延米的质量，为结构跨长，ξ 为结构阻尼比，为真实结构刚度，为弹性阶段质量变换系数，为弹性阶段荷载变换系数。空爆荷载持续时间非常短，可简化为等冲量的线性荷载，GB 50038–2005《人民防空地下室设计规范》中，推荐采用等效空爆荷载：

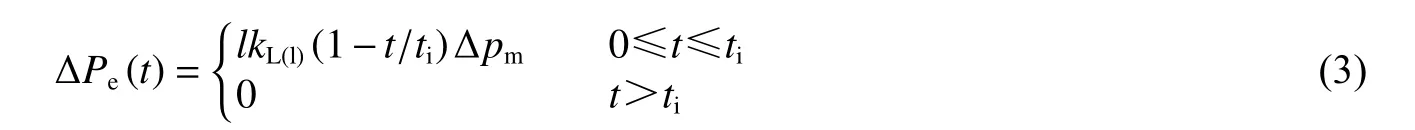
式中：为空爆荷载作用时长，为冲击波超压峰值，为弹性阶段荷载变换系数或塑性阶段荷载变换系数。

设结构弹性位移最大值对应的时刻为，对应的振动速度为，此为结构进入塑性振动的区分点，将弹性参数替换为塑性参数后，结构塑性阶段方程为：

式中：为塑性阶段等效结构质量，为塑性阶段等效结构阻尼，为结构最大抗力。各等效系数分别为：

式中：为塑性阶段质量变换系数。

1.2 结构分类及柔性结构弹性阶段动力响应求解

柔性结构指的是空爆荷载作用时长小于该结构振动从0 至最大弹性位移的时长，即＜；类似地，刚性结构指的是＞对应的结构，临界结构指的是=对应的结构。

求解空爆作用结构动力方程时，常采用杜哈梅积分方法，在求解过程中，会出现多次分部积分，计算过程复杂。根据微分方程理论：任意微分方程解答均可表示为通解与特解之和的形式，这个方法可一定程度简化本文动力方程的求解。

对于柔性结构，在弹性阶段且在荷载作用时长范围0≤≤，由初始位移和初始速度均为0，结合式(1)、(3)可求该强迫振动阶段解：

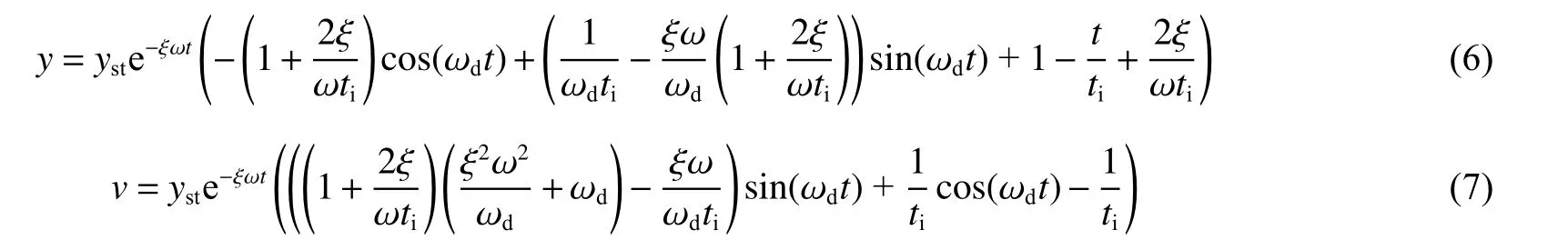
式中：ω 为无阻尼振动等效频率，ω为含阻尼振动等效频率，为超压峰值为静载时的结构位移。各参数计算公式为：

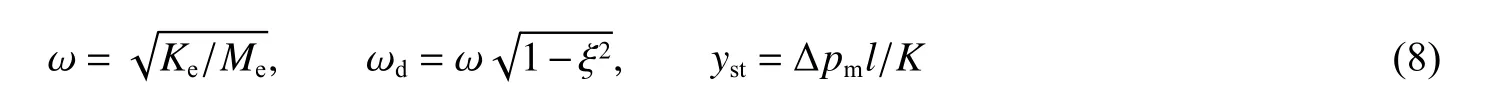
将代替代入式(6)～(7)，即可得到强迫振动结束时的位移、速度。当空爆荷载消去，这个阶段结构外荷载为0、以位移及速度为初始条件的含阻尼弹性自由振动（即当＜≤），可由式(1)、(3)求解：

式中：γ 为阻尼综合降低系数，θ、θ为结构时长参数。计算公式为：

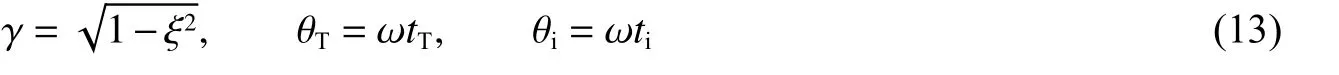
1.3 柔性结构塑性阶段动力响应求解

根据理想弹塑性理论假设，结构完成弹性振动后结构达到最大的抗力，在塑性阶段该抗力保持不变，此时为外荷载为0、以位移及速度为初始条件的含阻尼塑性阶段自由振动。由式(4)可得：

在达到弹塑性位移最大值时，此时振动速度=0。令式（15）右为0，得出：

将式(16)对应的时刻代入式(14)，得出结构弹塑性振动最大位移为：

代入等效单自由度体系对应参数，即将式(5)中、及代入(17)，可得：

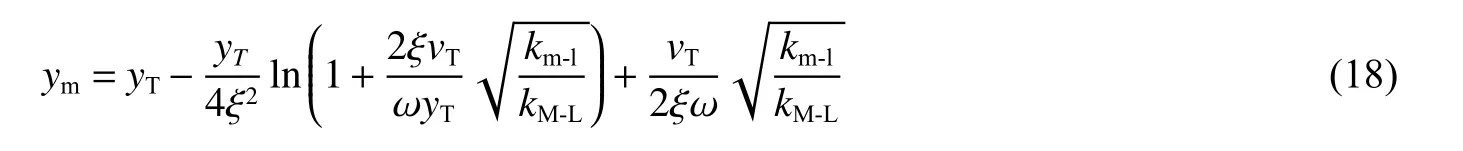
式中：、分别为弹性、塑性阶段质量变换系数与荷载变换系数的比。即：

由结构弹塑性理论及抗爆设计规范，弹塑性阶段抗力动力系数和延性比β 分别为：

将式(11)、(18)代入式(20)，且令：

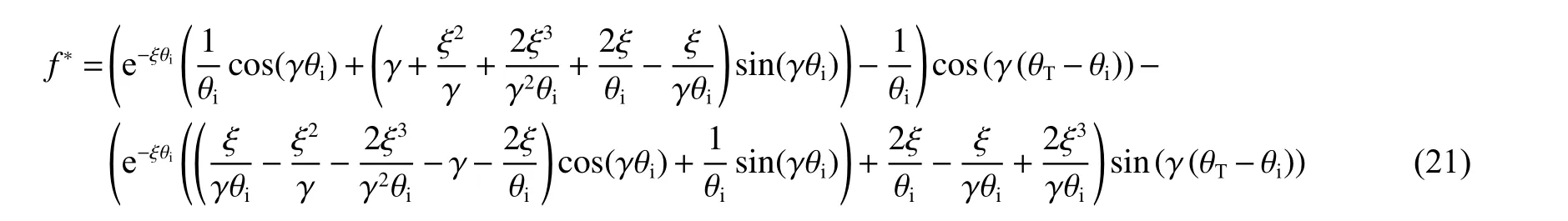
则得到柔性结构延性比β 关于抗力动力系数的表达式：

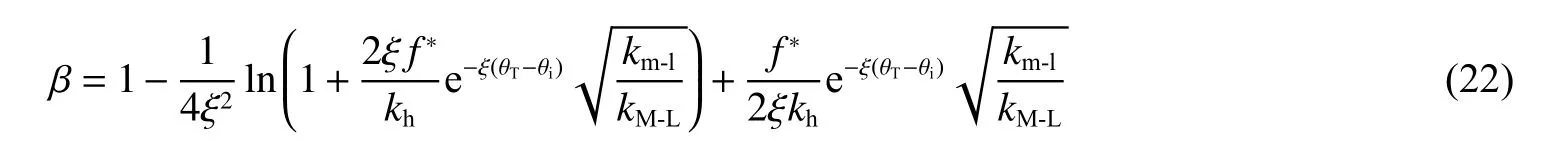
2 刚性及临界结构空爆作用动力响应求解

2.1 刚性结构弹性阶段动力响应求解

根据定义及理论分析可知，刚性结构弹性阶段（0＜≤）与柔性结构0＜≤时段的振动方程相同，将代入式(6)～(7)，可得时刻的位移和速度：

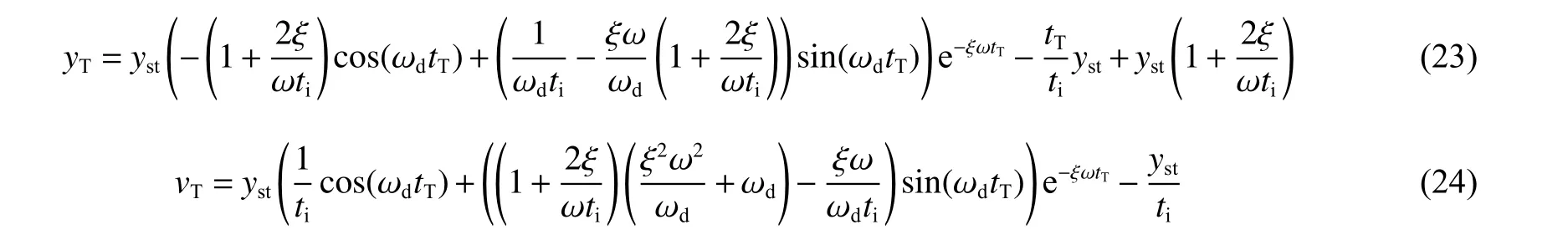
2.2 刚性结构塑性阶段动力响应求解

由定义可知，刚性结构从弹性振动进入塑性振动后，第1 个塑性响应阶段为外荷载不为0、以位移和速度为初始条件的含阻尼塑性阶段强迫振动，即在＜＜内，由式(4)求出其动力响应解答后，可得到时刻结构振动位移和速度分别为：

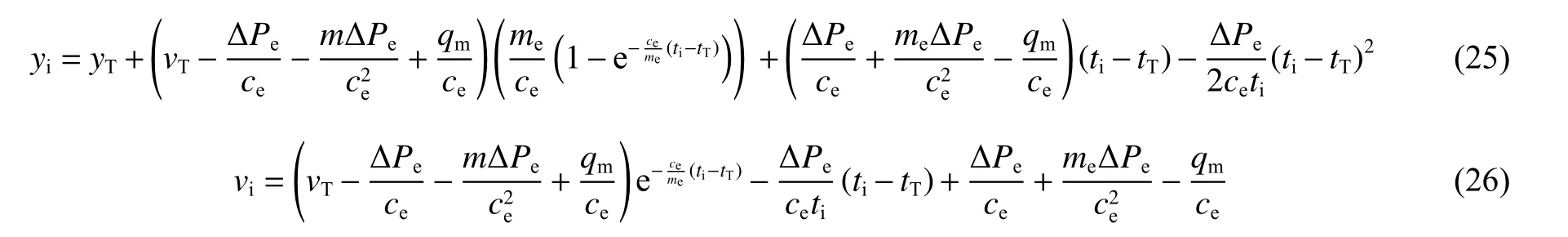
刚性结构振动＞时，为无外荷载、位移和速度为初始条件的含阻尼塑性阶段自由振动，即当＜≤时，该振动方程与柔性结构塑性阶段响应方程求解一致，将式(14)～(16)中用替换为后，便得出其解答，其中为：

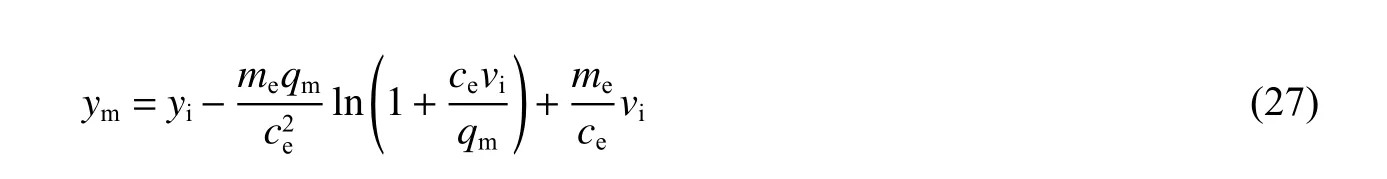
同理，将式(5)中、和代入式(27)后，可将等效单自由体系转变为原结构参数。为精简篇幅、清晰显示延性比对应的参数关系，本文中省略该化简过程。令：

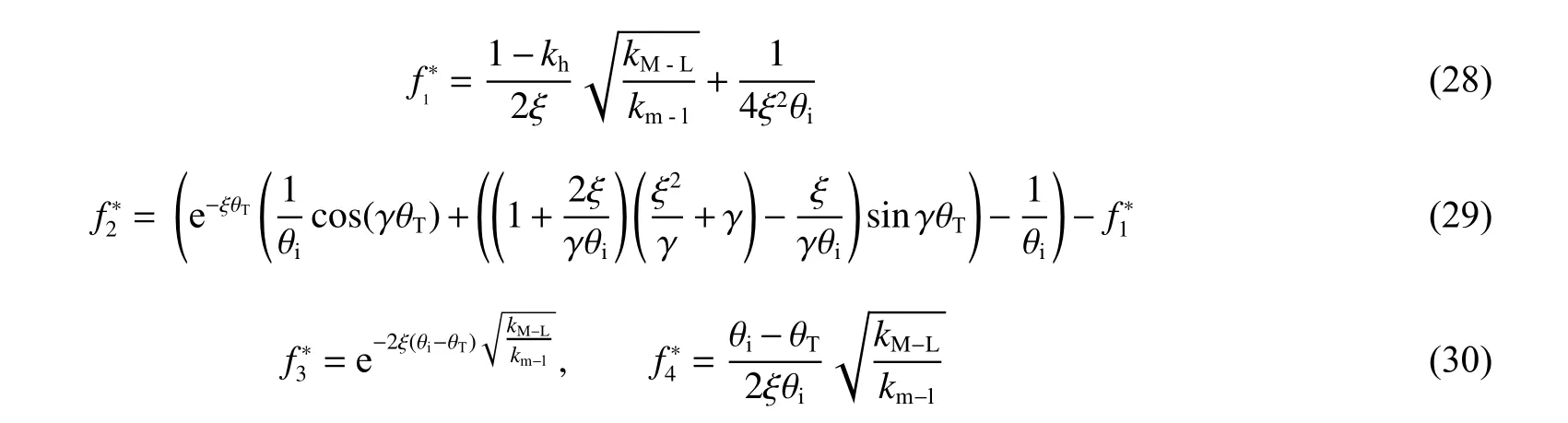
由式(20)、(23)和(27)可知，基于动力系数的延性比为：

2.3 临界状态结构动力响应求解

根据临界状态定义可知，空爆荷载作用时长与结构完成弹性振动时长恰好相等，即=。在弹性阶段且在荷载作用时长范围0＜＜，由弹性振动式(23)～(24)可得：

振动时刻大于时，外荷载为0、以和为初始条件的含阻尼塑性阶段自由振动，即当＜＜时，与柔性结构塑性阶段振动一样，即利用式(18)、(20)、(23)～(24)，且令：

可得临界结构基于动力系数的延性比：

由式(22)、(31)、(35)可以看出，将动力系数化解为关于阻尼比、延性比等参数的显性表达式难度很大，几乎不可能。因此，采用本文公式进行考虑阻尼的动力系数分析时，可根据结构类型的界定条件迭代计算。

3 算例验证

3.1 算例工况遴选

GB 50038–2005《人民防空地下室设计规范》中，推荐采用等效单自由振动动力系数计算方法。无阻尼、不含塑性参数的简化公式为：

为了校核本文公式的精准性，以式（36）为对比前提，以简支梁为结构选型，以文献[1]中推荐的钢筋混凝土构件允许延性比1～4 为计算范围，以文献[23]中推荐的空爆结构-荷载参数θ≤2.2 为参数范围；为了独立观察阻尼对动力系数的影响程度，选用典型的塑性参数，即弹性、塑性阶段等效质量系数与等效荷载系数之比、，由文献[5]取常数值0.78、0.66；在阻尼比为0.0001～0.1 时，选择5 种典型阻尼比，即0.000 1（接近无阻尼）、0.001（极小阻尼）、0.01（小阻尼，建筑钢构件可采用数值）、0.05（常用阻尼比，钢筋混凝土及砌体构件常采用数值）、0.1（较大阻尼，塑性阶段可能性数值）作为建筑物构件典型的阻尼比。共计20 种典型计算工况，见表1。

表1 典型工况Table 1 Typical calculation cases

为了查看动力系数与延性比、阻尼比的关系，考虑阻尼比后的20 种工况计算结果，与文献[1]中公式在延性比为1～4 时计算结果的比较，如图2 所示；各工况计算结果与文献[1]中公式计算结果的相对误差如图3(a)所示，与阻尼比为0.000 1 工况计算结果的相对误差如图3(b)所示。

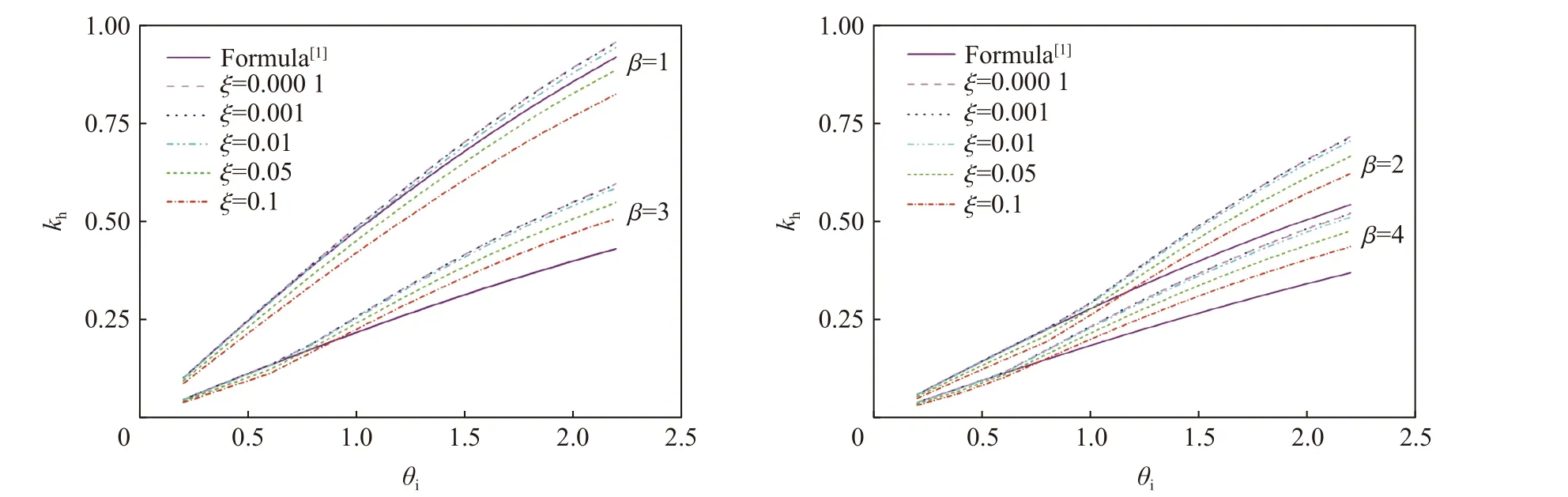
图2 本文工况计算结果与文献公式的比较Fig. 2 Comparison of the results from the calculation cases and from the code formula

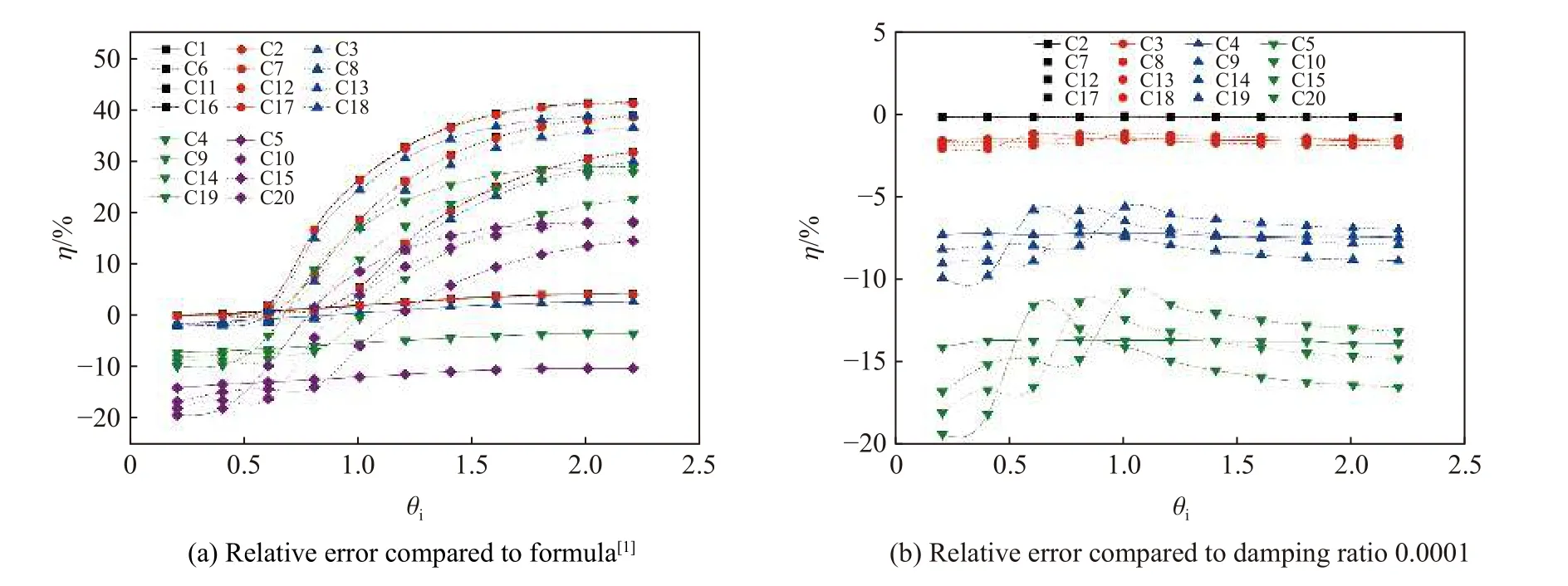
图3 本文工况计算结果的相对误差Fig. 3 Relative errors of the calculation cases

延性比β=1 表示弹塑性抗爆设计退化为弹性设计，此时各阻尼比的动力系数曲线均为光滑曲线。延性比增加表示结构的塑性变形比例增加，随着β 从2 递增到4，动力系数对参数θ的斜率从0.8 至0.6 附近发生转折。相同延性比数值下，阻尼比越大，动力系数越小，阻尼比为0.000 1（接近无阻尼）、0.001（极小阻尼）、0.01（小阻尼）的差异非常小。相同阻尼比情况下，随着延性比β 的增加，相同θ对应的动力系数降低。规范计算公式与柔性结构、临界结构计算结果差异很小，与刚性结构动力系数计算结果差异较大。

3.2 结果分析与讨论

由图2 可知，延性比β 为1 时：文献[1]中公式计算结果与阻尼比为0.0001～0.1 的计算结果差异均较小，低于阻尼比0.0001 的计算结果，最小为0.06%，最大为4.23%，平均为2.43%；文献[1]中公式计算结果位于阻尼比0.01 与0.05（常用阻尼比）之间，相差最小值为0.07%，最大值为2.63%，平均值为0.86%；阻尼比为0.1 时，差异变得显著，平均值为11.73%。可见，用文献[1]中公式进行弹性阶段抗爆设计具有很高计算精度和优势，可观察到增加5%以上的阻尼比，对抗爆设计具有明显的经济效益。

由图3(a)可知：延性比β 为2～4 时，文献[1]中公式计算结果与柔性结构、临界结构计算公式的计算结果差异很小，略低于阻尼比0.0001、0.001 的，略高于阻尼比0.01～0.1 的，其差异为0～4%，用文献[1]中公式进行柔性结构抗爆设计仍具有较高精度；而较大幅度低于本文刚性结构的计算结果，在阻尼比0.0001～0.1 下，延性比β=2 时最大差异为31.88%～14.52%，延性比β=3 时最大差异为38.83%～18.25 %，延性比β=4 时最大差异为41.49%～18.09%。这种差异与文献[1]中忽略阻尼比及塑性参数有关，也与文献[1]中拟合公式时选择的类型有关。

由图3(b)（以阻尼比0.0001 对应的动力系数为基准）可知：阻尼比为0.001 时，动力系数结果降低有限，其差异为−0.11%～−0.20%，基本可以忽略，说明结构阻尼比在0.001 以下，可按无阻尼进行结构抗爆设计；阻尼比为0.01 时，动力系数值略有降低，其差异为−1.49%～−2.08%，数值较小，在结构设计允许范围内，可忽略该阻尼比对结构的影响；阻尼比为0.05 时，动力系数值降低明显，平均值为−7.33%～−9.92%；阻尼比为0.1 时，对应的动力系数降低非常明显，动力系数值降低平均值为−13.42%～−19.43%；阻尼比大于0.05 时，临界结构的动力系数差异性明显低于柔性结构、刚性结构数值，即对于大多数抗爆结构，不应忽略此时的阻尼影响，可增设阻尼构造来降低抗爆设计的工程造价。

4 结 论

推导了空爆作用下柔性结构、刚性结构和临界结构等效静载动力系数的隐式函数表达式，通过典型计算工况，分析了阻尼比对动力系数的影响，得到以下结论。

（1） 阻尼比0.001、0.01 较阻尼比0.0001 的动力系数值降低幅度约0.20%、2.08%，即阻尼比小于0.01 时，数值差异性很小，即可忽略阻尼比小于0.01 对抗爆设计动力系数影响作用。

（2） 阻尼比0.05、0.1 较阻尼比0.0001 的动力系数值降低幅度约9.92%、19.43%，说明将抗空爆结构的阻尼比提高至0.05 以上，将产生有较大的经济效益，是一种良好的抗空爆设计手段。

（3） GB 50038–2005《人民防空地下室设计规范》中，空爆动力系数计算公式忽略阻尼比、塑性参数，对完成弹性阶段抗爆设计具有很高计算精度和优势。当进行弹塑性抗爆设计时，规范中公式较适用于柔性结构、临界结构抗爆设计，且误差在4%以内。运用于刚性结构时，规范中公式均小于本文中计算公式计算结果，且阻尼比越小误差越大，延性比β=4 时相对差异值可达18.09%～41.49%。