粗骨料粒径对混凝土动态压缩行为的影响研究*

王江波，丁俊升，王晓东，杜忠华，高光发

（南京理工大学机械工程学院, 江苏 南京 210094）

混凝土材料是一种由水泥砂浆基体与粗骨料颗粒组成的应变率敏感的工程复合材料，其动态冲击下的力学行为与准静态状况下有着显著的区别。随着应变率的增加，混凝土材料的抗拉强度与抗压强度都有明显的增加，这种率效应是由于水泥基体的微裂纹扩展和粘弹性特性引起的。SHPB 装置是研究混凝土材料动态力学性能最常用的试验装置，可以获得其应变率在10～10s范围内的冲击力学行为。粗骨料通常占混凝土混合体积40%以上，在混凝土的力学性能和物理特性方面起着重要的作用。事实上，与传统的金属材料不同，在材料动态力学性能测试试件的尺度上，粗骨料的影响是不可忽视的。

当前，土木工程领域的国内外学者分别对大尺寸混凝土试件静态力学性能和准细观尺寸效应开展了一些试验研究，研究表明：不同受力状态、不同截面形状、不同强度的混凝土准静态力学性能的尺寸效应非常明显，且该效应与试件尺寸、试件形状和材料强度耦合。同时，混凝土准静态三点弯曲试验、准静态压缩和拉伸试验表明，粗骨料尺寸和含量对混凝土准静态力学性能、破坏能量和裂纹扩展形态皆具有非常明显的影响。Hao 等对最大骨料粒径为4 和8 mm 的混凝土和砂浆试件进行了SHPB试验，试验结果表明：含骨料的混凝土试件动态增长因子总高于砂浆试件，并且随着骨料粒径的增大，混凝土的动态增长因子减小。Kim 等对最大骨料粒径为13、19 和25 mm 的砂浆和混凝土进行了SHPB 试验发现：纯率动态增长因子随着应变率的增加而增加，但不同最大粗骨料尺寸的总体结果对动态增长因子没有显示出很强的影响。Li 等对骨料最大粒径为7.5 mm的方形和圆柱形试件进行了SHPB 试验，结果表明圆柱体试件的动态抗压强度高于立方体试件，即试件形状对抗压强度也有一定的影响。Grote 等进行了骨料对平板冲击试验混凝土材料动态增长因子的影响，并对粗骨料体积率从0%增加到42%进行数值模拟研究，结果表明混凝土试件的动态强度得到了提高。Cadoni 等对含有粗骨料最大尺寸为25 mm 的混凝土试样进行Hopkinson 钢筋束拉伸试验，发现骨料的含量越小，试件的动态拉伸强度和能量吸收能力越高。

动态增长系数（动态增长因子，动态抗压强度与准静态抗压强度之比）常用来衡量混凝土材料的应变率效应。研究人员提出了各种经验公式来描述混凝土材料的动态增长因子与应变率的关系，其中使用最广泛的是CEB-FIP 方程。CEB 模型表明，在应变率为30 s时，动态增长因子和对数应变率(l gε˙)曲线中存在斜率的突变。Bischoff 等根据不同文献的研究结果对动态增长因子与应变率的关系进行了综合评述，认为在动态冲击下（约10 s），混凝土的抗压强度比准静态压缩强度高出85%～100%，但试验结果有很大的离散性。高光发等对近30 年相关文献中混凝土的动态压缩和拉伸试验数据进行总结，得到了混凝土材料在不同应变率区间的强度动态增长因子预测表达式。

1 试验方法

1.1 试验材料

试验材料为中强度砂浆和混凝土，试验原材料包括硅酸盐水泥、河砂、粗骨料、矿粉、水和减水剂，不同粗骨料粒径的混凝土与砂浆相比，除了增加相同体积分数的粗骨料以外，其它材料及配比完全一样。另外，为了保证强度达到设计要求以及试件的准确性，对粗骨料进行了水洗和烘干的预处理，减小其含泥量。由于本试验中研究不同粒径对混凝土力学性能的影响，故对粗骨料进行筛选，得到4～8 mm、10～14 mm 和22～26 mm 这3 个范围的粗骨料尺寸，可认为粗骨料等效平均粒径分别为6、12 和24 mm。

试验中加工了砂浆强度型号为M60 的砂浆试件，在此基础上制备出3 种不同粗骨料尺寸的C60 混凝土，配合比如表1 所示，需要说明的是，这里的C60 标号与传统的标号意义不一致，这里是指M60 砂浆添加粗骨料后的混凝土，其目的是为了研究粗骨料对混凝土力学性能的影响。同时选用3 种粗骨料，其粗骨料平均粒径分别为6、12 和24 mm，每种粒径的质量占比都相同。混凝土试件的命名规则为砂浆等级以及加入粗骨料的平均粒径，比如对于C60-G6 混凝土为M60 的砂浆和平均粒径为6 mm 的粗骨料均匀混合加工而成。

表1 不同材料试样的配比Table 1 Mix proportion of different grades of mortar and concrete

按照表1 的配合比制备尺寸为1 000 mm×1 000 mm×400 mm 混凝土和砂浆靶板，根据规定进行常规养护时间28 d，然后通过钻孔取芯切割的方法获取试件，对试件的两端面进行打磨，使试件的两端面平行度小于0.2°，打磨后的试件直径为68 mm，准静态和动态压缩试件长径比分别为2.0 和0.5。

1.2 准静态压缩试验

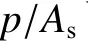
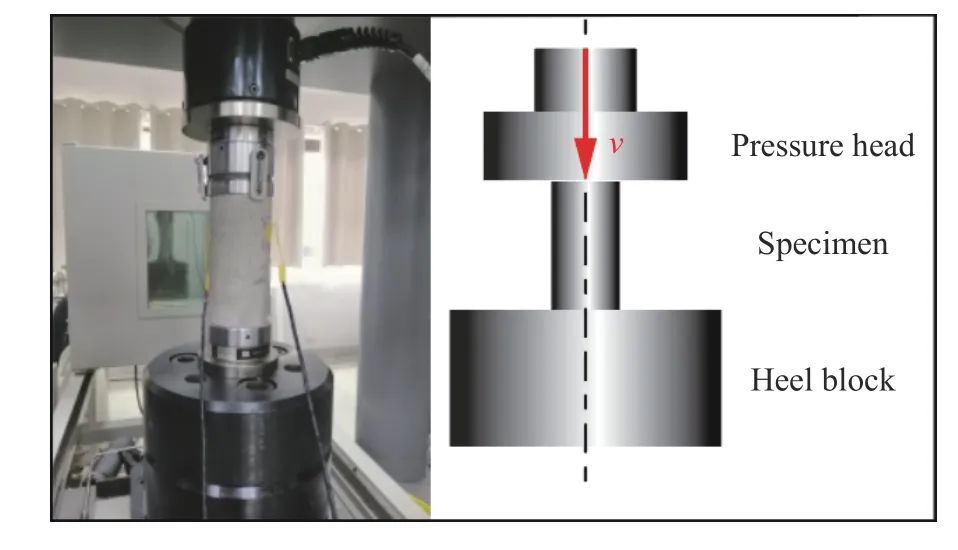
图1 准静态压缩试验Fig. 1 Quasi-static compression test

图2 为准静态压缩条件下不同类型试件的应力-应变曲线。需要说明的是，每种试件共获得3 条有效的曲线，准静态压缩的屈服强度应为其3 个有效数据的平均值，为了展示材料的应力应变曲线，选取应力峰值在中间的曲线为典型的应力-应变曲线。

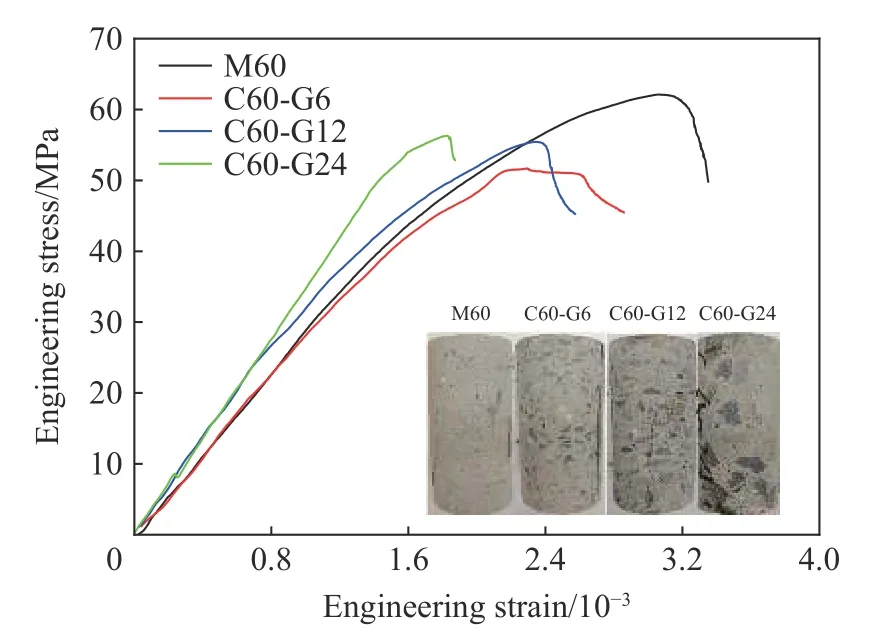
图2 准静态压缩下的应力-应变曲线Fig. 2 Quasi-static compressive stress-strain curves

1.3 动态压缩试验

1.3.1 SHPB 试验装置

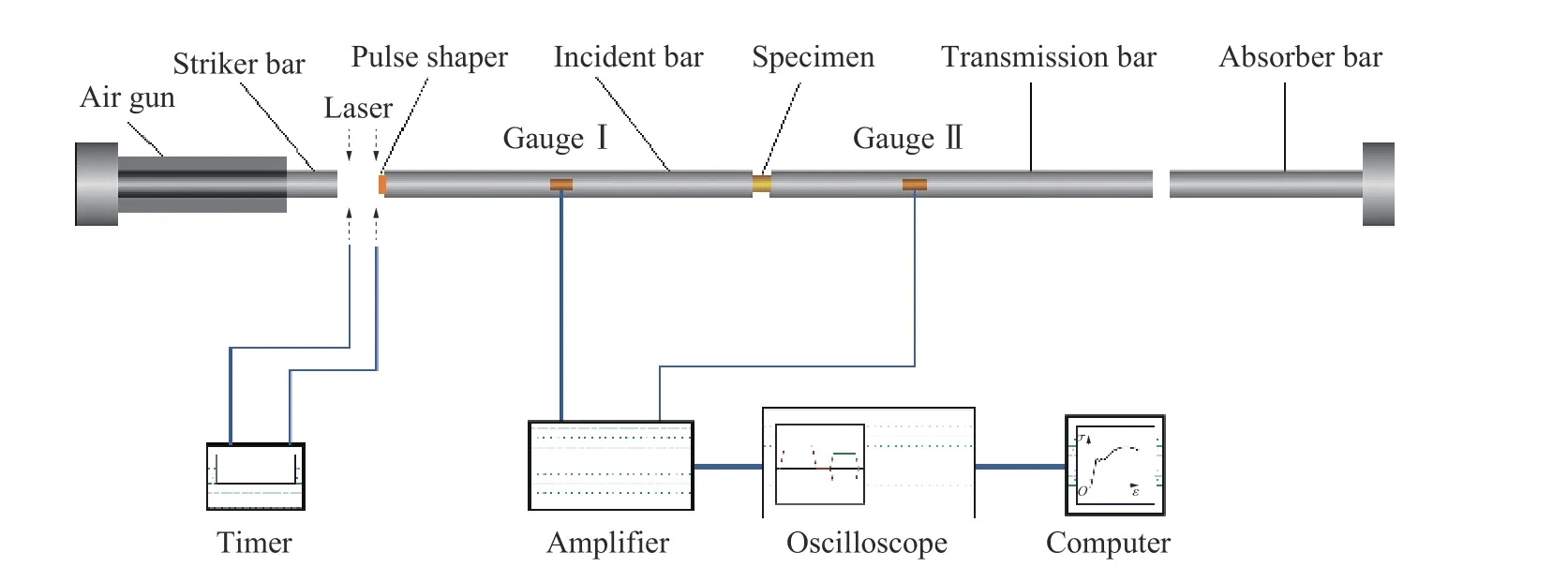
图3 SHPB 试验装置Fig. 3 Schematic of the SHPB test system

表2 SHPB 装置中部件的主要参数Table 2 Specifications of the SHPB experimental system

1.3.2 双脉冲整形器使用

混凝土的动态压缩破坏应变通常小于1%，因此需要缓慢升高的入射应力使试件内部应力均匀。然而，常规SHPB 试验（无脉冲整形器）产生的入射应力迅速增大，会导致混凝土试件在达到峰值应力之前发生破坏。为此，在SHPB 试验中采用了脉冲整形技术，以保证试件处于动态应力平衡和恒应变率加载状态。在本研究中，将直径为8～12 mm 和24～40 mm 的橡胶和T紫铜放置在入射杆的撞击端作为脉冲整形器，如图4(a)所示。试件放置于入射杆与透射杆之间（图4(b)），撞击杆冲击时，较小的橡胶首先变形，消除了入射脉冲中的高频振荡波，保证了试件端面与加载杆的充分接触。然后，较大的紫铜片对入射脉冲进行整形，产生加载脉冲，使试样失效。通过改变脉冲整形器的厚度和直径，可以调整入射脉冲的形状。

图4 试验时整形器与试件位置图Fig. 4 Position of the pulse shaper and the specimen in the experiment

1.3.3 应变率的确定

混凝土试件的SHPB 试验中整个加载区域内很难实现恒定的应变率，而关于应变率的取法也众说纷纭。有的文献对整个加载过程的应变率求平均值认为是代表应变率，然而，这种不能表征试件破坏时的真实应变率，可能导致得到的应变率大于实际情况。Kim 等将试件应力峰值达到最大点对应的应变率定义为代表应变率。但是这种方法只能代表试件失效时的应变率，并不能完全表征试件在整个压缩过程中的应变率。本文中，代表应变率采用应变率平台段初始至试件达到最大应力之间范围的平均值，并对此进行线性拟合，如图5 所示。这种应变率的选取方法可以表征试验过程中试件应力上升至破坏的整个过程。

图5 典型试件的试验结果Fig. 5 Typical test results of specimens

1.3.4 动态应力平衡

众所周知，利用SHPB 装置进行混凝土材料的动态力学性能测试时，必须保证试件在加载过程中的恒应变率变形和轴向的动态应力平衡。这是由于在SHPB 动态压缩试验时，试件的应力、应变和应变率计算都是基于一维应力波和轴向动态应力平衡假设。试件两端的应力可计算获得弹性关系：

所以，为了表征试件在破坏时是否达到动态应力平衡状态，一些学者定义了一个动态平衡因子]用来表示试件前后应力的差异，定义为：

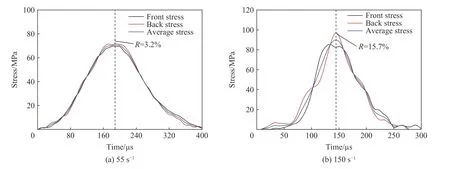
图6 试件的动态应力平衡状态Fig. 6 Dynamic stress equilibrium in the specimens

2 试验结果和分析

2.1 动态压缩应力-应变曲线

图7 为M60、C60-G6、C60-G12 和C60-G24 材料在不同应变率下典型的应力-应变曲线，并与准静态压缩试验下相应的应力-应变曲线进行了比较。从图中可以看出，4 种材料的应力应变行为具有明显的应变率效应，即随着应变率的增加，抗压强度逐渐增大；同时，4 种材料的应力-应变曲线呈现出相似的变化趋势，即初期应力与应变呈线性关系，随后为非线性阶段，当应力到达峰值以后急剧减小，使得试件破坏。应力应变曲线的下降阶段说明了峰值应力后的应变软化现象，试件开始出现不同程度的破碎。砂浆和混凝土试件的应力-应变曲线在动态和准静态压缩的初始阶段重合，这说明4 种材料的弹性模量没有应变率效应。

图7 不同应变率下试件的动态应力-应变曲线Fig. 7 Dynamic stress-strain curves of specimens at various strain rates

关于混凝土材料强度的应变率效应有不同的解释。Bischoff 等和Hao 等认为混凝土中的自由水在动态压缩时会产生Stefan 效应，即内部孔洞中自由水的运动会阻碍裂纹的扩展。Cotsovos 等认为这是SHPB 试验中试件端面摩擦效应引起的横向惯性效应，并不是真正的应变率效应。Ma 等认为在动态压缩试验时，试件内部裂纹的扩展速度远低于应力波的加载速度，裂缝并不只是沿薄弱区域产生和扩展，同时还会穿过粗骨料颗粒。短时间内试件内部的冲击能量累积增大，导致其强度增大。

2.2 压缩强度和动态增长因子

不同平均骨料粒径的混凝土和砂浆的动态抗压强度与应变率的关系如图8(b)所示，很明显，抗压强度随着应变率的增加而增加。图8(b)还显示，在相同的应变率范围内，C60-G12 混凝土的动态抗压强度最高，与准静态压缩状况有很大的差别（图8(a)）。这说明当加入了粗骨料后，混凝土的准静态压缩强度会随着骨料平均粒径的不同而出现差异，但总体都低于砂浆的抗压强度。然而，加入粗骨料后会增强混凝土的动态抗压强度。

图8 不同试件压缩强度与应变率的关系图Fig. 8 Relationship between the compressive strength and the strain rate of different specimens

现在已经广泛用于评价应变率效应对混凝土类材料的影响。研究表明：类混凝土材料的动态增长因子与应变率的对数呈线性关系。基于这些结果，学者们给出了混凝土材料抗压强度动态增长因子一些表达式，下面列出了几种被广泛应用的模型。

CEB 方程根据应变率、准静态应变率和准静态压缩强度给出了计算动态增长因子的经验公式：

Tedesco 等根据动态压缩试验给出了混凝土动态抗压强度的动态增长因子表达式：

式中：从低应变率敏感到高应变率敏感的过渡应变率为63.1 s，比CEB 模型中的要高出一些。

Zhou 等基于岩石材料的SHPB 试验结果拟合了动态增长因子与应变率对数的一个经验公式：

Hartmann 等基于文献中混凝土材料的动态压缩试验结果得到了动态增长因子经验公式：

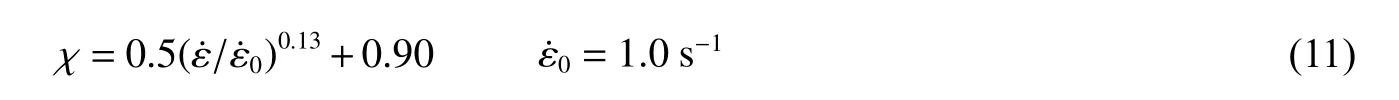
Lee 等提出了一种混凝土抗压强度动态增长因子与纯应变速率的经验公式，此公式中消除了试验中横向惯性效应对动态增长因子的影响：

Al-Salloum 等基于最小二乘法得到了抗压强度动态增长因子与应变率的多项式分布：

使用文献中模型的经验公式做出的曲线并和本文中试验所得的动态增长因子一同绘制在图9 中。图9 证实上面的公式都不能很好地描述M60 砂浆和不同粗骨料平均粒径混凝土的动态增长因子演变，这些模型一部分低估或高估了试件的动态增长因子，一部分对于临界转换应变率的定义不适用本文中的试验结果。究其原因，认为现阶段文献中动态增长因子的经验公式大多数都是基于混凝土类材料的强度来进行拟合的，并没有区分砂浆、骨料粒径以及含量等对动态增长因子的细致影响。因此，当进行研究时，会发现利用上面提到的模型会与本文中的结果有一定的差异。Bischoff 等建议混凝土材料的动态增长因子和应变率可以表达为：

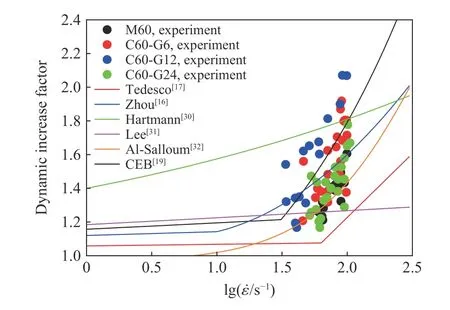
图9 试验动态增长因子与不同模型对比Fig. 9 Comparison of DIFs with different models

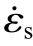
图10 不同骨料粒径的混凝土动态增长因子与应变率关系Fig. 10 Fitting curves of the dynamic increase factors and the strain rate for different aggregate sizes

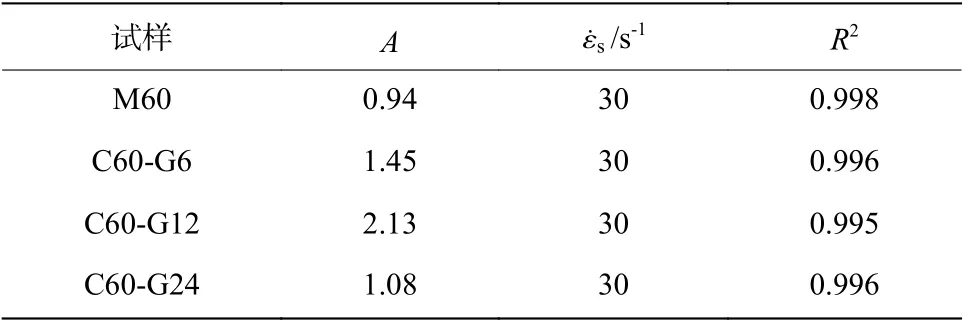
表3 不同试样的动态增长因子在公式中的拟合结果Table 3 Fitting results of dynamic increace factors of different samples in the formula

2.3 粗骨料粒径对动态增长因子的影响

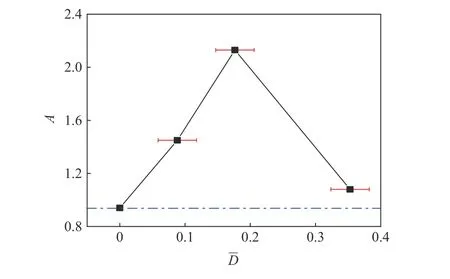
图11 无量纲粗骨料尺寸与应变率强化因子的关系Fig. 11 Relationship between the dimensionless coarse aggregate size and the strain rate strengthening factor

3 结 论

（1）在准静态压缩条件下，M60 砂浆的抗压强度高于C60 混凝土的抗压强度，且随着粗骨料平均粒径的增加，混凝土的抗压强度呈现出先增大后恒定的趋势；

（2）动态加载下，不同粗骨料粒径混凝土和对应砂浆材料的抗压强度都有明显的应变率效应，在本文的动态应变率范围内（40～110 s），C60-G12 混凝土的动态抗压强度高于其他类型的混凝土和砂浆；

（3）不同粗骨料粒径混凝土的动态增长因子均高于砂浆材料，表明粗骨料对混凝土材料的动态抗压强度具有增强作用，定义了粗骨料无量纲尺寸来评价粗骨料粒径的尺寸效应，即随着的增加，应变率强化系数呈现出先增大后减小的趋势。