先借再还巧解题
黄旭军

由于昨天的作业同学们完成得非常好,阿木老师进教室后大大地表扬了大家。阿木老师说:“大家表现这么好,这节课就讲一个故事吧!”同学们一听乐坏了。阿木老师清清嗓子,讲了一个国王出征的故事。
从前有位国王要领兵出征,出发前他想检阅一次军队。于是,他命令士兵按照每10人1排的方式排好,谁知排到最后缺1人。国王认为这样不吉利,就改为每9人1排,可最后又缺1人;改成每8人1排,仍缺1人;每7人1排又缺1人……直到每2人1排还是凑不齐。国王非常沮喪,以为老天跟自己过不去,不到3000人的队伍怎么也排不齐,只好收兵不再出征。
阿木老师这时停了下来,环顾四周,向同学们发问:“哪位同学能猜出国王的兵有多少吗?”同学们面露难色,不知如何算才好!
阿木老师得意地继续讲:“要想每排人站齐,总人数必须是每排人数的倍数。如果是10,9,8,7,…,2的公倍数,那么无论怎样排都是没有问题的。而国王的兵怎么排也缺少1人,如果先借1人……”。
阿木老师突然不讲了,这时算得快的同学已经有结果了。“老师,如果先借1人,总数就是10,9,8,7,…,2的最小公倍数。而10,9,8,7,…,2的最小公倍数是2520,再还1人就是2519。所以国王的兵有2519人。”数学王子迅速地说出了他的思路。
阿木老师哈哈一笑,说道:“这种‘先借再还’法,还可以解决更多难题。”同学们这才发现,原来不知不觉中又被老师“骗了”——什么讲故事,分明就是在学数学好吧!阿木老师趁机又出了2道例题。
计算 1
2+1
4+1
8+1
16+1
32+1
64+1
128 的结果。
直接通分,分母都变成128。
1 2+1 4+1 8+1 16+1 32+1 64+1 128
=64 128+32 128+16 128+8 128+4 128+2 128+1 128
=64+32+16+8+4+2+1
128
=127 128
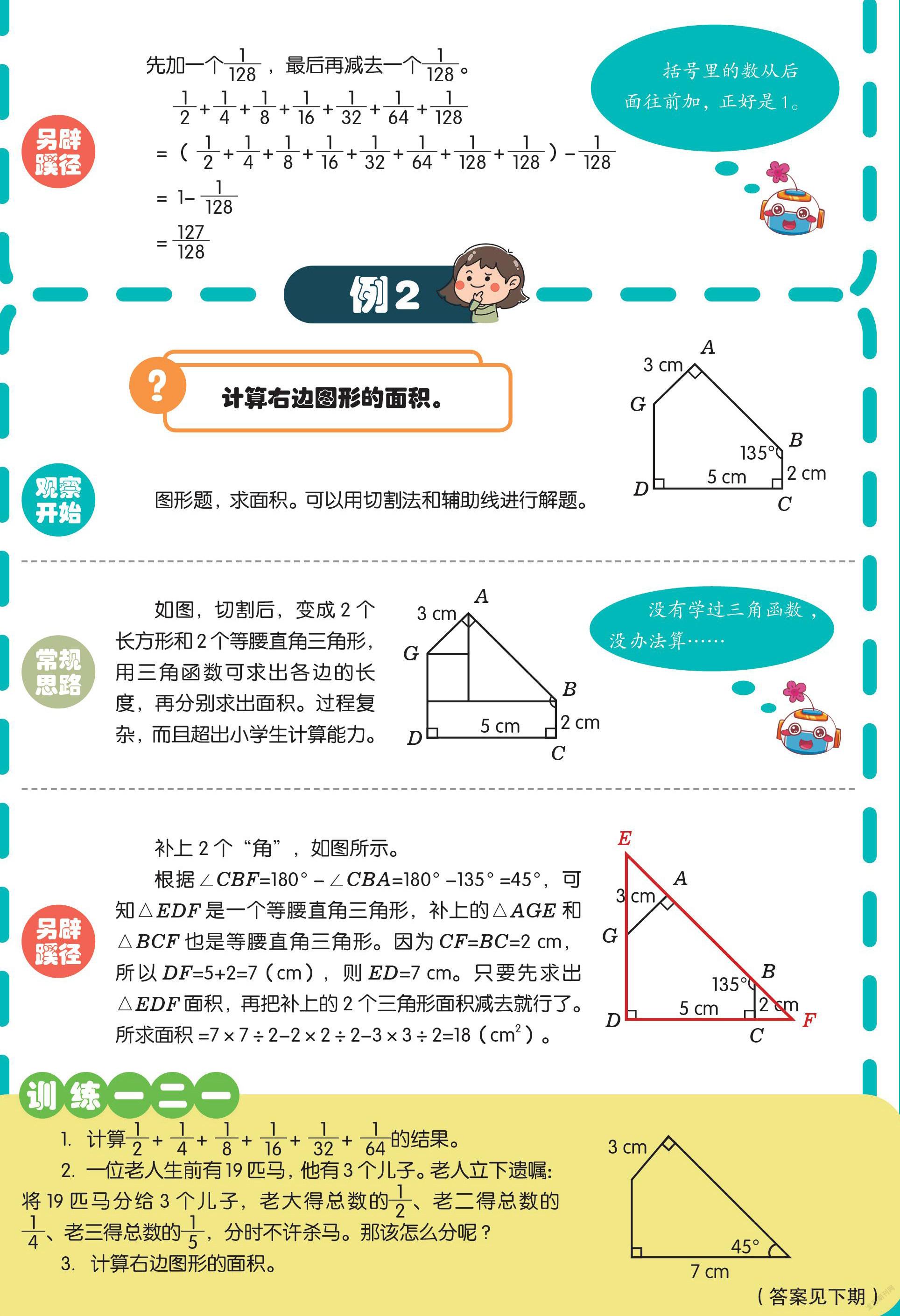
如图,切割后,变成2个长方形和2个等腰直角三角形,用三角函数可求出各边的长度,再分别求出面积。过程复杂,而且超出小学生计算能力。
补上2个“角”,如图所示。
根据∠CBF=180°-∠CBA=180°-135°=45°,可知△EDF是一个等腰直角三角形,补上的△AGE和△BCF也是等腰直角三角形。因为CF=BC=2 cm,所以DF=5+2=7(cm),则ED=7 cm。只要先求出△EDF面积,再把补上的2个三角形面积减去就行了。所求面积=7×7÷2-2×2÷2-3×3÷2=18(cm2)。
1.计算1 2+1 4+1 8+1 16+1 32+1 64的结果。
2.一位老人生前有19匹马,他有3个儿子。老人立下遗嘱:将19匹马分给3个儿子,老大得总数的1 2、老二得总数的1 4、老三得总数的1 5,分时不许杀马。那该怎么分呢?
3.计算右边图形的面积。
3864500316577

