化难为简数个数
秦浩然

周末,爸爸妈妈带我去海边玩。可是“天有不测风云”,台风光顾,我们的游玩计划泡了汤,只能窝在酒店里。
我百无聊赖地从酒店房间往外看,突然发现沙滩上有一块巨大的电子屏幕。仔细一瞧,原来整个大屏幕是由一些长方形的小屏幕组成的。我赶紧把这一大发现告诉妈妈。妈妈问道:“如果把一块小屏幕看成一个小长方形,你能算出这块大屏幕里一共有多少个长方形吗?”
这可难不倒我,我把这块巨大屏幕的大概样式画在纸上。
数图形要讲究“不遗漏、不重复”的原则。我可以先数1个小长方形,再数由2个小长方形拼成的长方形,然后依次数由3个小长方形拼成的长方形、由4个小长方形拼成的长方形……细想一下,这样一一列举也太麻烦了,有没有更加简单的方法呢?
我仔细审视着纸上的图形,发现图形的第1行是由5个小长方形组成的。
这一行里一共有5个单个的小长方形、4个由2个小长方形组合成的长方形、3个由3个小长方形组合成的长方形、2个由4个小长方形组合成的长方形和1个由5个小长方形组合成的长方形,这样第1行一共有5+4+3+2+1=15(个)长方形。大屏幕中一共有4行这样的图形,那就有15×4=60(个)长方形。
再把第1行、第2行合并看,如图1。
忽略这个图形中的虚线部分,那么和上述情况一样共有15个长方形。而整个大屏幕中像这样2行合并在一起的长方形有3个,即一共有15×3=45(个)长方形。
然后把第1行、第2行和第3行合并起来,如图2。
同样忽略图形中的虚线部分,那么和上面一样,也共有15個长方形。而整个大屏幕中像这样3行合并在一起的长方形有2个,即一共有15×2=30(个)长方形。接着,把4行合并起来,如图3。
同样把图形中的虚线部分忽略,数长方形的方法同上,共有15个长方形。这样,整个大屏幕中长方形个数的总和为60+45+30+15=150(个)。
我激动极了,但是生怕出错,想了想有没有更好的方法。对了!其实在探究过程中我们不难发现,这个图形每一行的长方形个数为15,正好是这些长方形的长的线段数。刚才我已经知道高为1行的长方形一共有4种,高为2行的长方形一共有3种,高为3行的长方形一共有2种,最后高为4行的长方形为1种。共有4+3+2+1=10(种)这样的长方形,这正好是这些长方形的宽的线段数。最后,长方形的总个数就是长方形的长的线段数×长方形的宽的线段数=15×10=150(个)。
哈哈,这样就更简单了!不算不知道,一算吓一跳,一个由20个小长方形组成的大长方形巨型屏幕竟然隐藏了这么多的长方形,真是太神奇了!这可能就是数学带来的惊喜吧!
指导老师 陆 霞
李 军 3月4日 11:19:32
浩然也太厉害了吧,去海边玩也能从周边的事物中发现一道数学题。果然,数学就是要靠仔细的观察和严谨的思考,这样才有机会像数学家那样想出一个个厉害的数学定理。
刘朵朵 3月4日 14:18:10
浩然给出了2种数图形的方法。一种是1行1行、2行2行……地数,另一种是利用线段的数量来数图形。其中,数线段的重要规律是:单条线上线段的总数,都等于从1开始的几个连续数的和(有几条独立线段就有几个连续数)。这个数线段的规律,也可以扩展到数图形上。
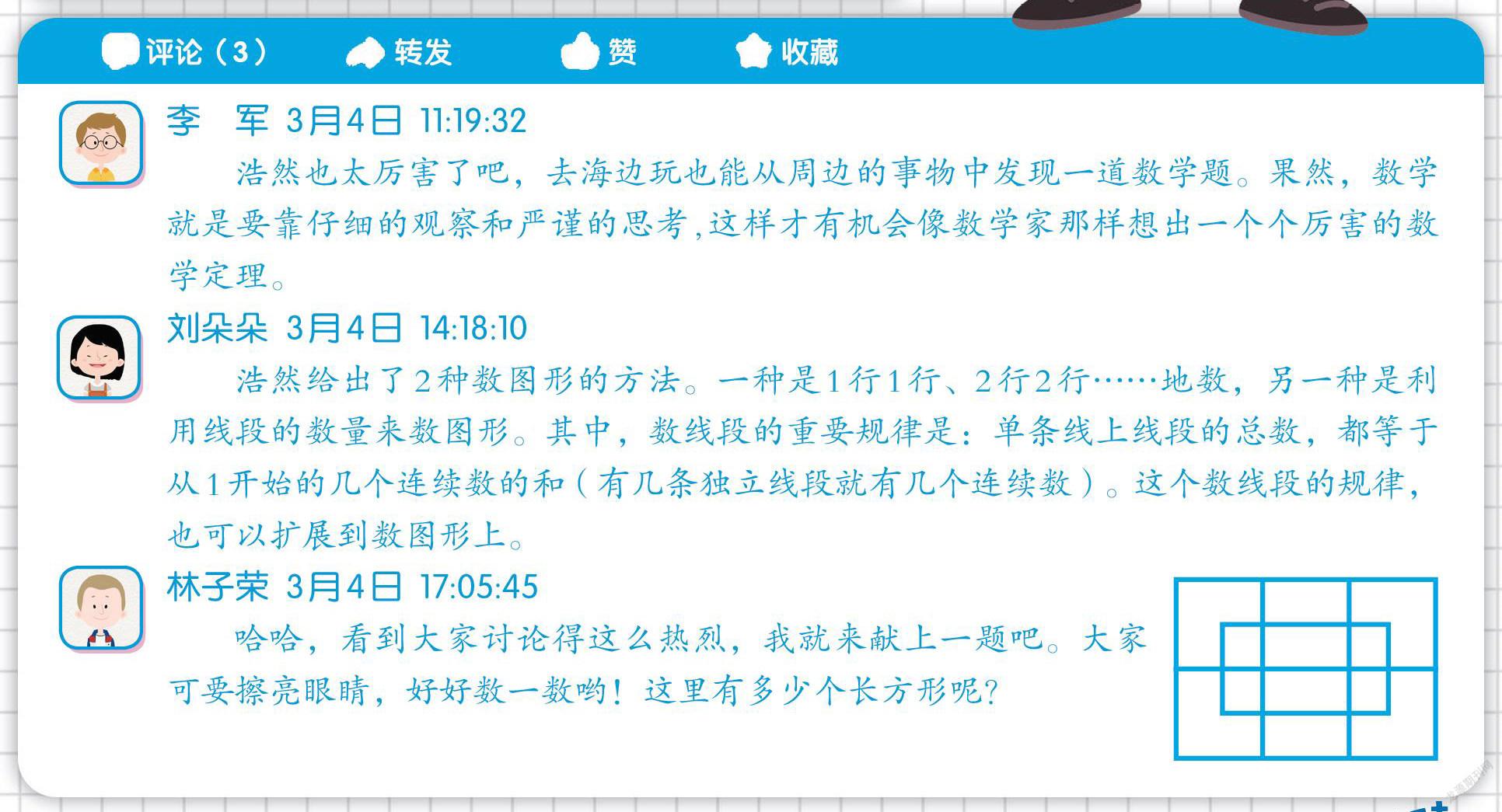
林子荣 3月4日 17:05:45
哈哈,看到大家讨论得这么热烈,我就来献上一题吧。大家可要擦亮眼睛,好好数一数哟!这里有多少个长方形呢?
3025500316546

