一种跨项目缺陷预测的源项目训练数据选择方法

盖金晶,郑 尚,于化龙,高 尚

(江苏科技大学计算机学院,江苏 镇江 212100)

在软件开发的过程中,需求分析、软件设计以及开发人员的编码实现,每个过程都有可能由于开发人员的经验不足而出现软件缺陷. 这些软件缺陷可能会引起意想不到的问题,严重的情况下会给公司造成不可挽回的损失. 在软件开发的过程中不可避免会出现软件缺陷,而越早发现缺陷并且越早修复它们,则付出的代价越小. 若软件发布后,修复缺陷的成本将大大增加. 我们希望在软件开发初期就能够有效地检测出缺陷.

跨项目软件缺陷预测(cross project defect prediction,简称CPDP)旨在软件开发初期通过其他项目的历史数据,来构建软件缺陷预测模型,再在当前项目上进行预测,从而得到可能存在的潜在缺陷.

近年来,越来越多的研究者开始关注跨项目软件缺陷预测. 主要围绕同构跨项目缺陷预测(homogeneous cross-project defect learning)和异构跨项目缺陷预测(heterogeneous cross-project defect prediction)两方面. 其中,同构是指所有源项目和目标项目具有相同的度量元,而异构是指源项目与目标项目具有不同的度量元,根据具体情况,源项目之间也可能具有不同的度量元. 而本文则是针对同构跨项目缺陷预测开展研究.

Jureczko和Madeyski[1]从代码所有权(code ownership)角度,考虑了3种不同类型(工业界、开源界、学术界)的项目,对CPDP的可行性进行了分析. 他们的研究结果表明,跨项目进行软件缺陷预测的结果并不理想.

Turhan[2]为了深层次分析研究造成CPDP性能不理想的原因,引入了数据集漂移(dataset shift)的概念. 他们通过对数据集漂移类型进行分析,推荐了两类解决方法:基于实例的方法和基于分布的方法. Zimmermann等[3]基于项目的上下文因素进行分析,共提出了40种不同的项目上下文因素来计算项目间的相似性. 他们的研究为源项目的选择提供了指引.

由于大量不相关的跨项目数据往往使建立高性能的预测模型变得困难. 为了克服这一挑战,许多研究人员专注于筛选与CPDP任务无关的源实例或特性.

Turhan等[4]提出了Burak过滤法,他们通过计算训练集与目标项目中实例的欧式距离,选出最近的K个实例添加到训练集中. 他们的实验结果表明,Burak过滤法能有效地提高CPDP模型的性能. He等[5]提出了一种两阶段的筛选方法TDS.第一阶段他们根据目标项目度量元的分布特征取值,通过欧式距离筛选出前K个候选源项目;第二阶段从前K个候选源项目中通过Burak过滤法或Peters过滤法[6]选出与目标项目最为接近的实例. 李勇等[7]随后提出了相似的两阶段筛选方法,他们根据余弦距离选出与目标项目最为相关的前K个候选源项目,随后借助Peters过滤法进一步选出相关实例.

除了上述基于实例选择的研究成果,国内外学者也对基于分布的跨项目缺陷预测开展了相关研究. Nam等[8]提出一种迁移学习方法,迁移学习通过调整源项目,使得源项目与目标项目的特征相似. 并且他们进一步拓展TCA,得到TCA+来提升跨项目缺陷预测性能.

Zhao等[9]提出了NN过滤器,他们通过删除那些不在目标项目数据的最近邻居中出现的源项目实例,这样使得源项目和目标项目在分布上更加相似. Ma等[10]提出了一种名为transfer naive Bayes(TNB)的方法,该方法首先通过data gravitation(DG)方法[11]对源实例进行权重调整,以削弱不相关源数据的影响,然后对这些权重调整后的源数据构建朴素Bayes分类器.

最近,一些研究表明,在目标项目中添加一定比例的标记数据,可能有助于提高CPDP的性能. Chen等[12]提出了一种新的方法(DTB),它在目标项目中使用少量的标记数据,同样使用DG方法初始化源项目数据的权值,然后利用TrAdaboost[13]建立预测模型,利用目标项目中有限数量的标签数据对源数据进行重估.

上述跨项目缺陷预测方法虽已经取得了一定的成果,但是仍有改进的空间. 具体来说,即基于相似性选取的方法仍不精确,同时盲目使用大量的训练数据所训练出的预测模型容易导致较高的误报率,因此,本文在一对一同构跨项目缺陷预测领域做了相应的改进工作:

(1)从数据分布的角度,利用JS散度测算找到与目标项目最相似的源项目,提升源项目选取的准确度;

(2)提出相对密度,对选定的源项目进行数据选择,提高预测模型的精度;

(3)通过实验验证,本文方法对不同项目的训练集和分类器的选择,皆表现出较好的性能.

1 相关概念

1.1 JS散度

JS散度也称JS距离,是KL散度的一种变形. Kullback-Leibler divergence(KL散度[14])又称为相对熵,信息散度,信息增益. KL散度是两个概率分布P和Q差别的非对称性的度量.典型情况下,P表示数据的真实分布,Q表示数据的理论分布、模型分布、或P的近似分布.那么离散变量KL散度见式(1):

(1)

由于KL散度不具有对称性,即KL(P||Q)≠KL(Q||P),为了解决这个问题,有人提出了Jensen-Shannon divergence(JS散度)[15]作为相似度度量的指标.现有两个概率分布P和Q,其JS散度公式如式(2):

(2)

在计算JS散度的过程中使用了蒙特卡洛[16]方法(Monte Carlo),蒙特卡洛法是一种用来模拟随机现象的数学方法,这种方法在模拟中能直接反映过程中的随机性.如公式(3)所示:

(3)

不同于KL散度,JS散度的值域范围是[0,1],相同为0,相反则为1. 相比较于KL,对相似度的判别更准确了. 同时其对称性能让散度度量更准确. 因此,本研究拟利用JS散度去衡量任意两个项目的相似性,即JS散度越接近,两个项目的分布也就越相似.

1.2 相对密度

经过JS散度选定与目标项目分布最为相似的源项目需要对其训练数据选择,以便构建预测模型. 一般来说,若能精确地测出每一个训练样本的概率密度,从噪声点和离群点中区分出具有重要信息的样本则变得比较容易. 但是,在高维特征空间中,获得精确的概率密度是极为困难的,要获取相对精确的概率密度也是十分耗时的. 因此,本文采用了一种避免概率密度测量的方法,即精确提取任意两个训练样本的概率密度的比例关系,我们称这种反映比例关系的信息为相对密度.

为了计算相对密度,本文使用了与基于K最近邻概率密度估计法(K-nearest neighbors-based probability density estimation,KNN-PDE[17])相似的策略. 作为一种非参数概率密度估计方法,KNN-PDE通过测量每个训练实例的K最近邻距离来估计多维连续空间中的概率密度分布. 当训练实例的数量达到无穷大时,从KNN-PDE获得的结果可以近似收敛到实际概率密度分布. 因此,本文提出的相对密度策略也采用了K最近邻距离估计相对密度.

图1 研究框架Fig.1 Research framework

(4)

显然,在相对密度方法中,K值的选择是十分重要的.若K值太小,则很难将低样本从普通样本中区分出来;若K值太大,则那些重要样本与低样本的区别便会变得模糊不清,而这些微小的差距将更难获取.因此,需要给参数K选择合适的值.

2 研究方法

文章以源项目数据选择为研究对象,从项目分布的相似性角度出发,首先利用JS散度进行源项目选择,其次提出相对密度进行训练数据选择,最后采用CPDP中常见的分类器对数据进行训练,并将模型用于目标项目的预测. 具体的研究框架和方法描述分别见图1和表1.

2.1 数据标准化

本文使用Z-Score标准化方法来处理数据. Z-Score标准化方法是常见的数据处理方法,通过将不同量级的数据转化为同一量级Z-Score分值进行比较.

表1 研究方法Table 1 Research method

该方法计算出原始数据的均值μ和标准差σ,对数据进行标准化处理. Z-Score标准化方法的公式可表示如式(5):

(5)

2.2 基于JS散度的源项目确定

本文在对候选源项目集使用Z-Score标准化处理之后,将进行JS散度的计算,进而完成源项目的确定.

根据前文描述,JS散度能够度量两个项目数据分布的相似度,且JS越小证明分布越接近. 因此,本节工作主要是计算所有源项目与目标项目的JS散度,并选取与目标项目最接近的源项目.

具体流程如表2所示. 首先,将候选源项目集和目标项目分别拟合混合高斯(Gaussian mixture model,GMM)[18]模型. 高斯混合模型可以看作是由K个单高斯模型组合而成的模型,这K个子模型是混合模型的隐变量(hidden variable). 一般来说,一个混合模型可以使用任何概率分布,这里使用高斯混合模型是因为高斯分布具备很好的数学性质以及良好的计算性能. 其次通过蒙特卡洛公式,计算候选项目集和目标项目的JS散度,其中JS(Si,T)表示为当前第i个候选项目与目标项目计算得出的JS散度值;并通过比较所得JS散度的大小,选取出与目标项目JS散度最小的源项目,即确定其为训练项目.

表2 源项目挑选流程Table 2 Source project selection

2.3 基于相对密度的源项目数据选择

挑选后的源项目仍包含少量的噪声或离群点样本,如若盲目选择将影响预测的效果. 为了筛选合适的训练数据,本文通过相对密度反映类别中每个实例的重要性,并有选择地截取数据,提高训练模型的精度. 具体的方法流程如表3所示.

首先,根据2.2选取的源项目,统计其所有样本数量,记为N;其次,计算每个样本与第K个最近邻的距离,获得相对密度;最后,根据相对密度进行重要性排序,同时设定阈值p(percent)选择合适数量的样本作为训练集. 由表3可以看出,参数K和p的设定将决定模型训练的质量,文中将在后续章节讨论两个参数的选择.

表3 源项目的训练数据选择Table 3 Training data selection of the source project

2.4 构建跨项目软件缺陷预测模型

为了证明我们方法的适应性,我们分别采取CPDP中常用的分类器逻辑回归(LR)、贝叶斯(NB)、支持向量机(SVM)、K近邻(KNN)训练预测模型,并用于目标项目加以验证,对得到的CPDP性能进行对比分析.

3 实验验证

3.1 数据集与评价指标

3.1.1 数据集

文中的数据集是来自Jureczko和Madeyski[19]收集的PROMISE库中的开源项目,其已经被广泛应用于跨项目缺陷预测研究. 表4展示了数据集的基本信息,包括项目名称、项目版本、实例数量和缺陷率.

表4 PROMISE数据集Table 4 PROMISE data sets

3.1.2 评价指标

在软件缺陷预测中,合理的评价指标能更好地评估预测结果,下文将介绍软件缺陷预测中的基本的评价指标.

软件缺陷可以看做是二分类问题,若将有缺陷的模块设置为正例,无缺陷模块为反例,则每个实例的分类过程中可能会出现以下4种情况:实际为有缺陷类被正确分类为有缺陷类,即真正例(true positive,TP);实际为无缺陷类被错误分类为有缺陷类,即假正例(false positive,FP);实际为无缺陷类被正确分类为无缺陷类,即真反例(true negative,TN);实际为有缺陷类被错误分类为无缺陷类,即假反例(false negative,FN). 在人工智能中,混淆矩阵是表示精度评价的一种标准格式,用n行n列的矩阵形式表示,如表5所示.

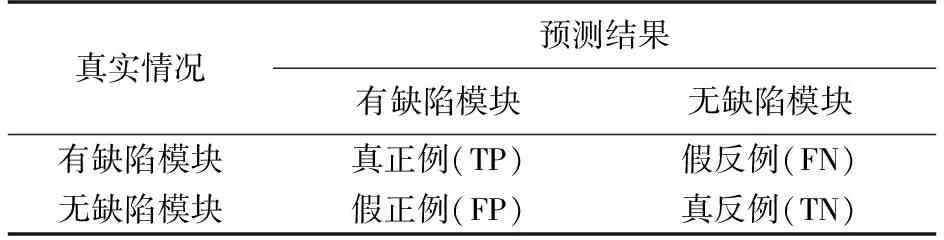
表5 混淆矩阵Table 5 Confusion matrix

根据上述描述,文章将采用F-measure作为本研究的评价指标,具体描述如下:

Precision:正确分类为正样本的实例数目与分类为正样本的实例数目的比率.

(6)

Recall:正确分类为正样本的实例数目与所有正样本实例数目的比率.

(7)

F-measure:对精确度和召回率的综合衡量.f值越高,表现越好.

(8)

3.2 实验设置与实验结果

本文为了确认本方法是否优于其他方法,我们在PROMISE数据集上与主流的跨项目缺陷预测方法以及设定的基线方法进行了对比.

首先,对8种方法进行简述,如下所示:

(1)DTB[12]方法:在目标项目中使用少量的标记数据,用来提高CPDP的效果.

(2)TrAdaboost[13]方法:构建预测模型,利用目标项目中有限数量的标签数据对源数据进行重估.

(3)TNB[10]方法:通过data gravitation(DG)方法对源数据进行权重调整,然后用权重调整后的源数据构建朴素贝叶斯分类器.

(4)TCA+[8]方法:转移成分分析方法,仅使用跨项目数据进行预测.

(5)NN filter[9]方法:通过删除非目标项目最近邻的源项目数据来对源项目数据进行筛选.

(6)KMM[20]方法:是KMM-MCW中的主要步骤,使用MMD最小化来对齐分布,降低域间差异,跳过概率密度估计,直接根据样本估计权重.

(7)KMM-MCW[21]方法:多分量权重(MCWs)学习模型来分析源项目中多个分量从而不断优化.

(8)基线方法:不做任何数据选择,直接对使用源项目训练模型进行目标项目预测.

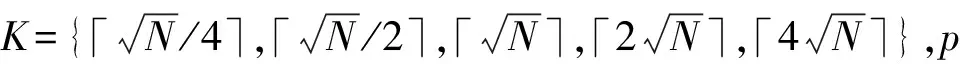
表6 各类方法的F-measure结果比较Table 6 F-measure comparison of various methods

除对比方法实验之外,本文为验证所提方法能够提高不同分类器构建的模型性能,在逻辑回归(LR)、贝叶斯(NB)、支持向量机(SVM)、K-近邻(KNN)这几种CPDP中常见分类器上也做了对比的实验,具体结果如表7所示.

表7 不同分类器下本方法获得的F-measure结果比较Table 7 F-measure comparison under different classifiers

根据表6结果可以发现,与其他方法相比,本文方法最终选取的训练数据在大多数项目上取得较高的F-measure,且整体结果的均值高于其他方法. 实验结果表明,本文方法能够在最大程度地利用源项目情况下,根据JS散度和相对密度选择合适的训练集构建预测模型,且获得较优的性能.

从表7可以发现,不同分类器结合本文方法在整体结果的均值都有了提升,且在大多数项目提高预测性能. 实验结果表明,本文方法能够适应于CPDP中常用的分类器,并提高模型性能.

4 参数讨论

图2展示了不同项目的K和p组合,相应的F-measure分布情况. 由图2可知,我们能够根据最优的F-measure找到合适的参数组合.

图2 不同K和p组合的F-measureFig.2 F-measure under different K and p

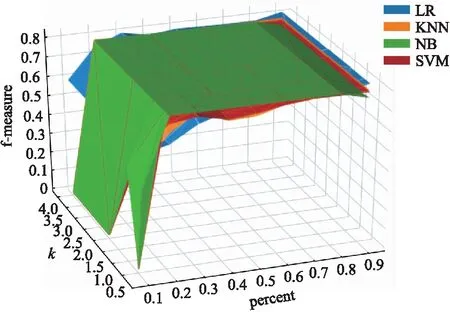
图3 xerces不同分类器的F-measureFig.3 F-measure of xerces under different classifiers

如图3所示,文章进一步讨论了K和p在相同数据集上的不同分类器下F-measure的值变化情况. 以xerces为例,图中结果表明,当F-measure值达到最高时,不同分类器在当前数据集上的K和p的组合基本保持一致,这说明经过本文方法所选择的训练数据已经达到最优,且能够适应CPDP中各类常用的分类器.

5 结论

本文围绕一对一的同构跨项目缺陷预测展开研究,主要针对源项目训练数据选择的问题,提出基于JS散度和相对密度的跨项目缺陷预测方法. 该方法首先利用JS(Jensen-Shannon divergence)散度选择与目标项目最相似的源项目;其次,提出基于相对密度的源项目数据选择方法;最后,采用CPDP中常见的分类器构建预测模型,并用于目标项目进行验证. 实验结果表明,在最大程度利用源项目的情况下,本方法不仅能够提高缺陷预测模型的性能,同时对不同分类器表现出较高的适应性.

后续工作中,我们将进一步在更多的软件缺陷数据集上验证方法的有效性,并对方法进行扩展,使其应用于多对一跨项目缺陷预测.