破产控制约束下组合投资:两阶段MiniMax模型

康志林, 王志焕

(1.华侨大学 经济与金融学院,福建 泉州 362021; 2.华侨大学 数学科学学院,福建 泉州 362021; 3.金融数学福建省高校重点实验室(莆田学院),福建 莆田 351100)

0 引言

自Markowitz的均值-方差模型诞生以来，理性投资者通常有两个目标：最大化收益和最小化风险。根据Markowitz组合投资理论，给定收益水平，通过最小化投资组合的方差可以获得最低风险；或给定投资者可以容忍的风险水平，通过最大化期望收益可以获得最高收益。除方差外，学者们从不同角度给出了投资组合风险度量方式，主要分为两类：一类是基于偏差-风险测度。如，Minimax风险测度[1]、下偏矩风险测度[2]。另一类是基于概率(分位数)-风险测度。如，在险价值(VaR)[3]。

在实际投资决策中，由于单期组合投资自身的局限性，自然地将经典的Markowitz均值-方差模型推广到多期情形，其中最具代表性的工作是Li和Ng[4]。此外，对投资者而言，要确认她的财富受益于多期投资组合策略，特别重要的一点是，在到达投资期限之前避免破产事件的发生。因此，破产风险控制是最优动态资产组合选择过程中需要考虑的一个重要因素。Zhu[5]提出了拓展的均值-方差模型，借以帮助投资者在收益-风险权衡意义下获得最优回报，且对破产具有良好的风险控制。Bielecki等[6]在连续时间框架下研究了破产控制约束下具有随机参数的均值-方差投资组合选择问题。在假定风险资产随机收益取决于随机市场的状态，并遵循马尔可夫链条件下，Wei和Ye[7]考虑了随机市场中带破产约束的多阶段均值-方差投资组合模型。徐维军等[8]基于可信性测度理论，根据Roy的定义给出了未来现金流量隶属三角模糊变量的控制破产风险的数学表达式，并构建了项目投资过程中受到破产风险因素影响的含破产风险约束的多项目投资组合决策模型。同样，Zhang和Liu[9]利用可信度理论，提出了具有破产控制的多阶段模糊投资组合选择的均值-方差模型。最近，Li等[10]研究了具有交易成本和破产约束的三阶段不确定多期投资组合选择问题，在模型中他们分别用不确定的期望值和方差来度量投资的最终财富和风险。易发现，除了徐维军等[9]，现有研究均基于均值-方差框架。本文拟在康志林和曾燕[11]基础上，类似文献Fu等[12](仅考虑两阶段)，对破产控制约束下两阶段MiniMax投资组合问题进行研究。

本文结构安排如下。第一部分，给出破产控制约束相关概念和多期MiniMax模型的数学结构。第二部分，在市场不允许卖空及含破产控制约束条件下，研究两阶段MiniMax模型的最优解析策略。

1 破产事件与多期MiniMax模型

考虑一个含n个风险资产Sj(j=1,…,n)的随机金融市场。投资者在零时刻以初始财富M0进入市场。投资者可以在接下来的T-1期将其财富按某一规则分配到n个资产中，并在第T期结束时获得最终财富。假设Rij为资产Sj在t期的随机收益率，rij为Rij的期望收益(t=1,,T,j=1,…,n)。定义向量Rt=(Rt1,…,Rtn)′和向量rt=(rt1,…,rtn)′，其中a′表示向量的转置。

设Vt-1为投资者在第t期开始时的初始财富，xij(j=1,2,…,n)为第t期开始时投资于第j个风险资产的金额。假设市场不允许卖空，即xij≥0。因此，财富演化方程可以表示为

(1)

(2)

当投资者的总财富在任何中间时刻或最后时刻低于预先设定的灾难阈值时，就会发生破产。如果投资者破产，由于其负债高、信用低，因而无法继续进行相应的投资。现记第t期的灾难阈值为b1，且将第t期的破产事件标记为BRt，则BRt事件发生的概率为[7]P(BRt)=P(Vt≤bt,Vi>bt,i=1,2,…,t-1),t=1,…,T。

P(BRt)=P(Vt≤0,Vi>0,i=1,2,…,t-1)

假设投资者是风险厌恶，即他或她希望最大化期末财富E(VT)，同时最小化期末总风险。这里，期末总风险定义为每项资产在一段时间内投资的最大绝对偏差之和，且从第1期到第期，每期的风险都不能超过给定的水平。因此，相应问题可以表述为一个具有两个相互冲突目标函数的优化问题:

min{wT,-E(VT)}

E(|Rtjxtj-rtjxtj|)≤εtE(Vt-1),t=1,…,T

通过引入风险厌恶系数λ∈(0,1), 将双目标线性规划问题转化为单目标参数优化问题:

2 两阶段MiniMax问题最优投资策略

E[f2(w2,V2)]

=λw2-(1-λ)E(V2)

s.t.q2jx2j≤z2,j=1,2,… ,n

定理1[11]对任意λ∈(0,1)，当

(3)

(4)

则问题(P2)的最优解为

(5)

(6)

其中，A12(λ),A22(λ)为拟投资的资产集。

由式(6)，易得

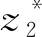
=V1a2

综上，有

=λw1+V1[λa2-(1-λ)·

=λw1-b2V1

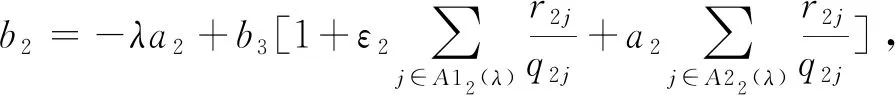
s.t.q1jx1j≤z1,j=1,…,n,q1jx1j≤ε1V0,j=1,…,n

s.t.q1jx1j≤z1,j=1,…,n

定理2对任意λ∈(0,1)，当

(7)

(8)

问题(P1)的最优解为

(9)

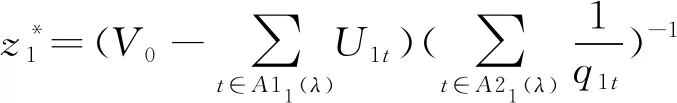
(10)

其中A11(λ),A21(λ)为拟投资的资产集，该集合由如下规则确定：

A11(λ)={n,n-1,…,n-k1},A21(λ)={m,m-1,…,1}，其中m=n-k1-1。

情形1当b2>0,如果存在整数k1≥0,k2≥0,k1+k2∈[0,n-3],n≥3使得

(11)

(12)

…

(13)

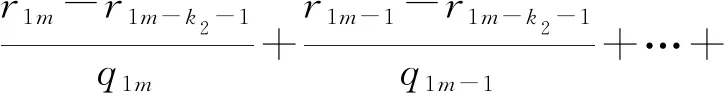
(14)

则A11(λ)={n,n-1,…,n-k1},A21(λ)={m,m-1,…,m-k2},其中m=n-k1-1。

情形2当b2<0，如果存在整数k1≥0,k2≥0,k1+k2∈[0,n-3],n≥3，使得

(15)

(16)

…

(17)

(18)

则A11(λ)={1,2,…,k1+1},A21(λ)={m,m+1,…,n-k2-1},其中m=k1+2。

3 期末总财富与总风险

根据式(1)、定理1和定理2的结论，可导出期末总财富E[V2]和总风险w2:

由于第t(t=1,2)期风险可表示为

因此，由式(2)可得第2期期末总风险