基于后悔理论的拼车决策问题研究

于晓娟, 邹正兴, 张千帆

(1.中南财经政法大学 工商管理学院，湖北 武汉 430073； 2.北京交通大学 经济管理学院，北京 100044; 3.华中科技大学 管理学院，湖北 武汉 430074)

0 引言

近年来，随着信息共享平台的普及，拼车引起了越来越多出行者的关注。拼车通常指相同路线的几个人同乘一辆车出行，或者车主在日常出行中捎带与自己行程相同或相近的乘客，车费可由乘客分摊。拼车出行通过共享的方式实现对车辆最大程度的利用，相当于提高了道路的有效通行能力，这在一定程度上降低出行成本并缓解交通压力。因此，对出行者单独驾车出行和拼车出行的决策行为进行研究具有重要意义。

早高峰拥堵的本质是高峰期出发时刻的选择问题。Vickrey[1]最早通过建立瓶颈模型刻画早高峰的通勤行为，得到了基于出行者出发时刻选择的均衡。经典瓶颈模型假设交通拥挤存在于瓶颈路段，当瓶颈处的车辆到达率超过其通行能力时会造成排队，因此经过该瓶颈路段的出行者不能全部准时到达目的地。较早到达瓶颈处的出行者面临较短的排队等待时间，同时面临较高的早到惩罚成本；准时到达目的地的出行者面临最长的排队等待时间；而较晚到达瓶颈处的出行者，面临较短的排队等待时间，同时面临较高的迟到惩罚成本。其主要思想是考虑出行者在高峰时段拥堵排队成本和其他成本(如计划延误成本和收费成本)之间的权衡。当没有任何一个出行者可以通过单方面改变其出发时刻来降低其出行成本时，系统达到均衡状态。随后，很多学者对瓶颈模型进行了拓展。Mahmassani[2]等在一个具有两条路径网络中分析出行者如何选择出发时间与路径的行为。Tabuchi[3]假设含瓶颈的公路旁有一条并行的地铁路线，研究不同收费体制下两种交通方式之间的竞争。Huang[4]研究了弹性需求下，私家车与地铁之间，通勤者如何选择出发时间与出行方式。此外，Huang[5]等研究了在一条具有瓶颈的高速公路上，同时具有私家车和公交车两种交通方式的出行者的出发时间选择问题。

上述文献均假设出行者是完全理性的，而在现实生活中，出行者的决策会受到自身的心理因素及有限认知能力的影响，其出行行为并非完全理性。特别地，出行者在做决策时往往会将已选方案的结果与其他方案的结果进行比较：若选择其他方案会带来更好的结果，则出行者会感到后悔；反之则欣喜。比如，拼车者在享受节约燃油费或者拥堵费的同时，需要承担较大的等待时间成本的风险。当拼车者的等待时间成本超过其他费用的节省时，该出行者往往因选择拼车出行而感到后悔。考虑到出行者通常会评估其对未来事件或情形的预期反应，因此考虑出行者的后悔厌恶心理对做出合意的决策具有重要意义。

后悔理论[6]认为出行者的出行方式选择不仅与所选方式本身的物理效用有关，且与另一个备选出行方式(选择集合中只有两个选择)比较后的后悔或高兴程度有关。目前，后悔理论在交通管理领域的研究主要集中于路径选择方面。比如，Chorus[7]等假设出行者对某一出行路径的选择依赖于该路径与其他备选路径中最好路径比较得到的后悔值，从而提出了随机后悔最小模型。随后，Chorus[8]用连续可微函数逼近度量后悔的连续不可微函数，构建了连续可微的随机后悔最小模型，它假设出行者对某一路径的选择依赖于其与每一个备选路径比较得到的后悔值之和。在此基础上，Chorus[9]又构建了一般化的随机后悔最小模型。李梦和黄海军[10,11]利用后悔理论研究了交通网络中出行者对出行路径选择的均衡。然而，鲜有文献利用后悔理论研究出行者的出行模式选择，特别是早高峰拼车决策问题。

基于此，为给出行者提供更好的出行策略和决策参考，本文引入后悔函数刻画出行者的后悔心理因素对出行模式选择的影响，认为出行者的出行模式选择不仅与所选出行模式本身的广义出行费用有关，而且与所有出行模式中最小的广义出行费用比较得到的后悔值有关。本文基于经典瓶颈模型构建了基于后悔理论的Logit随机用户均衡(SUE)模型，并分别考虑了不收费和最优收费两种机制。最后，通过算例验证了后悔厌恶程度对早高峰出行模式选择行为的影响。

1 基本模型

本节基于Vickrey瓶颈模型，计算在不考虑出行者的后悔厌恶心理时单独出行和拼车出行的出行成本，并对不收费和最优收费两种机制进行探讨。本模型考虑如下情形：N个同质的出行者每天早晨从住宿地出发去工作地，拥挤仅发生在一个具有确定通行能力的瓶颈处，其通行能力为s辆/单位时间。仅考虑单独驾车和拼车这两种出行方式，忽略公共交通、自行车等其他出行方式的影响，并假设每辆拼车中平均有m个出行者。单次出行的广义出行成本或费用由计划延误惩罚成本、出行时间成本、燃油成本、不便利成本及可能的拥堵费构成，分别如下：

1)计划延误成本。乘客在通过瓶颈时由于排队而引发的早到或延误惩罚成本。用t表示实际到达时刻，t*表示理想到达时刻(标准化为0)，β表示早到的单位延误惩罚成本，γ表示晚到的单位延误惩罚成本，则根据Small[12]和Arnott等[13]的理论可得计划延误成本为max{-βt,γt}。

2)出行时间成本。出行者的出行时间成本为单位时间的价值α乘以总的出行时间。

对于i(i∈{a,p})类型出行者而言，在t时刻到达时所需要的总出行时间TTi[t]等于瓶颈处的排队时间(当瓶颈处的到达率超过道路的通行能力时就会发生排队)加上自由流的行驶时间：

TTi[t]=Ti[t]+TTfI

(1)

其中，下标i=a表示单独驾车出行，下标i=p表示拼车出行；Ti[t]表示t时刻达到的i类型出行者在瓶颈处的排队时间，为队列中的总车辆除以道路的通行能力；TTfi表示模式i在自由流下的行驶时间。

(2)

此外，由于自由流的行驶时间对出行者的出发时间决策没有影响，不失一般性，在解析模型令TTfa=0，在数值模型再将其考虑进去。

3)燃油成本。平均燃油成本cfuel由单独出行者或拼车出行者平均承担。

4)不便利成本。拼车者因为和陌生人同行而降低舒适度和隐私感，从而面临固定的平均不便利成本θ。

5)可能的拥堵费用τ[t]。在收费机制下，需要考虑对出行者征收的拥堵费，对拼车出行者而言该费用由车内的m个人均摊。

注意，由于不同的政策会引发出行者不同的出行行为，本文考虑不收费和最优收费两种机制。其中，在最优收费机制下，收费可以消除所有的排队[9]。所以，在计算广义出行费用pi(i∈{a,p})时，不需要考虑排队带来的延误成本，但需要加上征收的拥堵费。

因此，单次出行的广义出行成本(不收费机制)ci[t]或费用(收费机制)pi[t]可分别表示为:

(3)

(4)

本文仅考虑同质的出行者，即所有人有相同的时间价值(α)及延误影子惩罚(β或γ)。每位出行者通过选择达到时刻来实现其出行成本的最小化。在达到均衡时，对于相同出行方式的出行者而言，任意出行者均不能通过单方面改变其出发时刻来降低其出行成本。下面分别讨论不收费均衡和最优收费均衡。

1.1 不收费均衡

均衡时需满足两个条件：1)从排队的开始时刻ts到结束时刻te瓶颈处通过的车辆等于总的车辆数；2)第一个出行者和最后一个出行者不会遇到排队，且他们的出行成本相等。可以表述为:

(5)

其中，qa和pp分别为选择单独出行和拼车出行者的人数，且满足qa+pq=N。

求解公式(5)可得:

(6)

由公式(3)可知，最早出发的出行者的广义出行成本为:

(7)

最后出发的出行者的广义出行成本为:

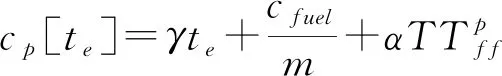
(8)

由于在均衡时所有单独出行者的出行成本均相同且与出发时间无关，同时所有拼车者的出行成本相同且与出发时间无关。由公式(7)和(8)可知，均衡广义出行成本为:

(9)

(10)

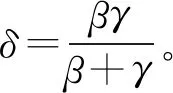
公式(9)和(10)表明，在不收费机制下，达到均衡时，每辆车的排队时长都以β/α的速率增加或γ/α的速率减小。此时，单独驾车者和拼车者混合出行，并共同排队通过瓶颈路段，其出行时刻与排队时长的关系如图1所示。

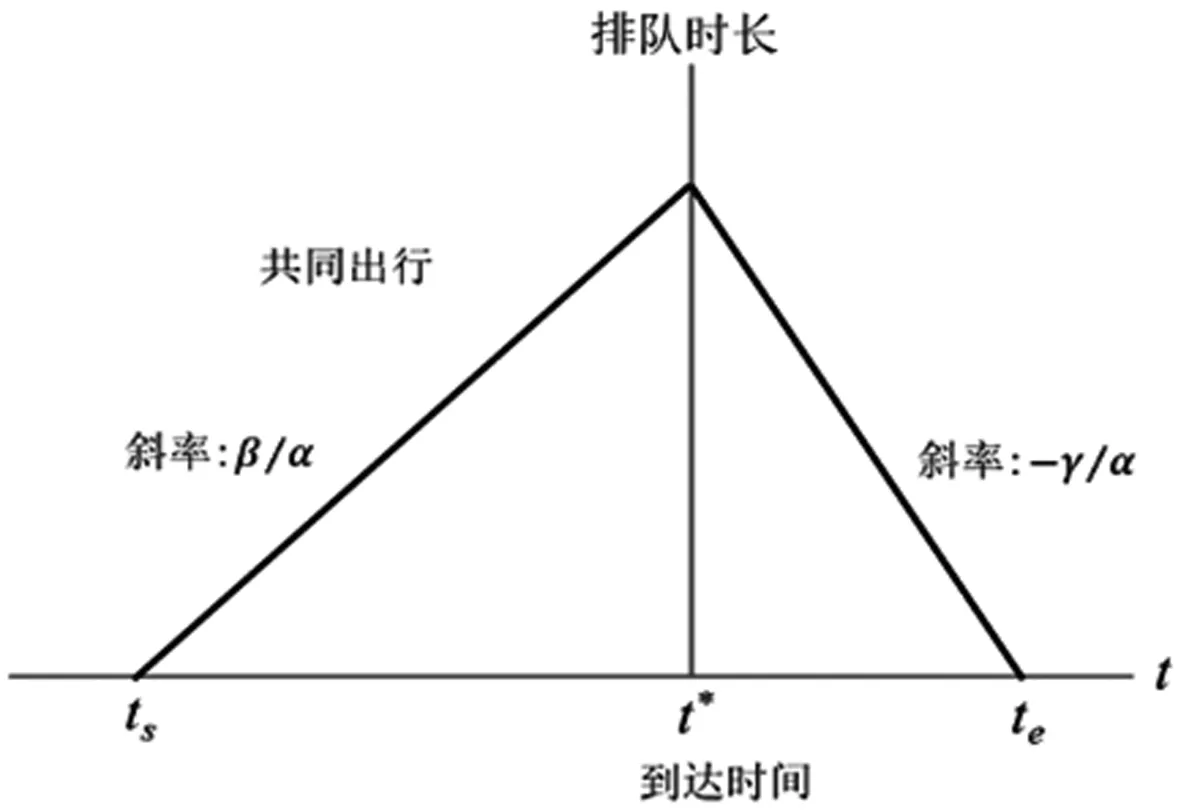
图1 不收费均衡下的排队时长

1.2 最优收费均衡

本小节考虑最优拥挤收费机制。在均衡时，对于早到的出行者，收费以速率β增加，而对晚到的出行者，收费以速率γ减少[19,20]。由于一辆拼车中有m个人，其带来的延误成本为单独出行的延误成本的m倍。因此，对于拼车出行者而言，其收费以mβ的速率增加或mγ的速率减小。在达到均衡时，拼车者和单独出行者分开行驶。具体地，拼车者选择通过瓶颈的中央，用较长的排队来换取较少的延误，而单独出行者选择避开瓶颈的中央，用较多的延误来换取较短的排队。因此，最优收费实现了单独出行和拼车出行的交通流的分离，如图2所示。

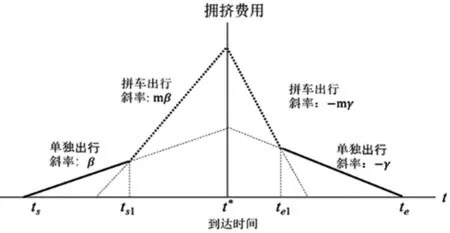
图2 最优拥挤费用

类似地，根据均衡条件(5)可得到收费的开始时刻ts及结束时刻te，如公式(6)所示。需注意，虽然最早出发时刻ts与最晚出发时刻te在收费机制和不收费机制下具有相同的表达式，其具体取值却不一定相同，因为表达式中的单独出行者人数qa和拼车出行者人数qp在两种机制下有不同取值。

由公式(4)和公式(6)可得，单独出行者的广义出行费用为:

(11)

为得到拼车出行者的出行费用，我们需先求其出行开始时刻ts1和结束时刻te1及ts1时刻的拥挤费τ[ts1]。

首先，由于交通流的分离，拼车出行者在瓶颈的中间时段出行。因此，ts1和te1满足如下条件：1)在到时间段内，瓶颈处通过的车辆等于总的拼车车辆数；2)ts1和te1出发的出行者具有相同的延误成本。可以表述为:

(12)

(13)

其次，由于均衡时ts处和ts1处有相同的出行价格，而最优收费可消除所有的排队，ts1时刻的拥挤费T[ts1]可由单独出行者的出行费用表示。均衡时，单独出行者和拼车出行者都不能通过单方面改变出行时间来降低其出行成本。因此，均衡的广义出行费用可表示为:

(14)

(15)

于是，由于改变出行模式所带来的出行成本的变化为:

Δp=pa-pp

(16)

公式(16)表明，在最优收费机制下，拼车和单独出行的价格差与单独出行者的数量有关。

2 基于后悔理论的早高峰出行模型

在基础模型中，我们利用经典瓶颈模型得到了不考虑后悔厌恶心理时出行者的广义出行成本及费用。而在考虑出行者的后悔厌恶心理时，出行者进行出行模式选择时不仅依赖于所选出行模式本身的出行成本，而且取决于与另一个备选出行模式的成本比较后得到的后悔或高兴。因此，本节对基础模型进行改进，构建一个兼顾基础模型中的广义出行费用与后悔厌恶的成本函数，并在此成本函数下研究出行者的出行模式选择。其中，当后悔厌恶水平为0时，改进的模型退化为第1节不考虑后悔厌恶水平时的模型。

假设所有的出行者有相同的后悔厌恶水平，构建新的兼顾广义出行费用和后悔感觉的成本函数hi(i∈{a,p})如下:

(17)

其中cmin=min{ca,cp},pmin=min{pa,pp}

(18)

R(λ,y)=1-exp(-λy),λ∈[0,+∞]

(19)

这里，cmin和pmin分别表示拼车和单独出行中最小的广义出行成本或费用，表示出行者的后悔厌恶水平，R(λ,y)是后悔厌恶函数。

根据(17)～(19)易知，后悔厌恶水平λ的广义出行费用差ci-cmin或pi-pmin越大，出行者感受到的后悔值-R(λ,cmin-ci)或者-R(λ,pmin-pi)越大。另外，ca、cp、pa和pp可分别由基础模型中的公式(9)、(10)、(14)、(15)获得。

我们以不收费机制为例来说明后悔厌恶函数R(λ,y)的性质。由cmin的定义可知，cmin-ci≤0且R(λ,cmin-ci)≤0。当cmin-ci=0时，R(λ,cmin-ci)=R(λ,0)=0，即当已选的出行模式的广义出行费用为最小时，出行者没有后悔感觉；当cmin-ci<0时，R(λ,cmin-ci)≤0。

用Hi表示出行模式i的感知“成本”，则Hi和hi的关系可写为:

Hi=hi+εi,i∈{a,p}

(20)

其中，εi表示感知“成本”的随机误差项，假设其服从独立相同的Gumbel分布。对于基于后悔理论的SUE模型的均衡解，出行者选择出行模式i的概率Fi和流量qi为:

(21)

其中，φ是用来度量出行者对感知成本误差敏感程度的参数。φ→0表示误差敏感度较低时，出行者等概率地选择每一种出行方式；φ→∞表示误差的敏感度较高时，出行者只选择感知成本最小的出行方式，此时SUE变成了UE。各出行模式的人数是由出行费用、出行者的后悔程度共同决定的。若出行者的后悔厌恶水平为0，则此模型退化到一般的SUE模型。

3 求解算法

本文采用迭代平均算法(MSA)求解均衡条件对应的随机用户均衡模型。具体步骤如下：

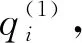
(22)

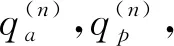
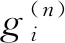
(23)

其中对任意i∈{a,p}，有:

(24)

4 数值算例

4.1 基础算例

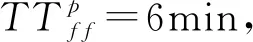
根据第3节提出的MSA算法可得该算例的结果，如表1所示。结果表明，收费可以促进拼车概率的增加(从0.09增加至0.40)。其原因是收费可消除所有的排队，而拼车在享受消除排队带来的好处之余，又可以和同乘者共同分担拥堵费用。在不收费机制下，单独出行的出行成本较低；而考虑后悔因素后，由于拼车可能会引发后悔，因此拼车者的出行成本(包含后悔因素在内)增加，而单独出行者的出行成本不变。相反地，在最优收费机制下，拼车出行的成本较低，而考虑后悔因素后，单独出行会引发后悔，从而单独出行者的出行成本(包含后悔因素在内)增加而拼车出行者的出行成本不变。

表1 础算例的结果

4.2 灵敏度分析

由于很难获取后悔厌恶水平的准确取值，本小节对其进行灵敏度分析，结果如图3所示。其中，图3(a)是参数λ对拼车的选择概率的影响，图3(b)是参数λ对不包含后悔的广义出行费用的影响，图3(c)是不收费机制下参数λ对包含后悔的广义出行费用的影响，图3(d)是收费机制下参数λ对包含后悔的广义出行费用的影响。

3(a) 后悔水平对拼车概率选择的影响

3(b) 后悔水平对不包含后悔的广义出行费用的影响

3(c) 后悔水平对包含后悔的广义出行费用的影响(不收费机制)

3(d) 后悔水平对包含后悔的广义出行费用的影响(收费机制)

图3(a)表明在不收费机制下，选择拼车的概率随后悔水平参数λ的增加而减小，当λ超过1.4时，选择拼车的概率几乎为0。这是因为在不收费时，拼车的出行成本总是高于不拼车，而后悔水平参数的增加又进一步增加了拼车的总的出行成本，当超过1.4时，拼车的出行成本将远大于不拼车，从而几乎没有人愿意选择拼车出行。相反地，在最优收费机制下，选择拼车的概率随着后悔水平参数的增加而增加。其原因是收费消除了排队，拼车的出行成本总是高于不拼车，而后悔水平参数的增加又进一步增加了不拼车的总的出行价格，进而提高了拼车的选择概率。

图3(c)表明，在不收费机制下，随着后悔水平参数λ的增加，不拼车的出行成本(包含后悔)剧烈增加，而拼车的出行成本(包含后悔)则保持不变。根据图3(a)可知，不收费机制下，当λ超过1.4时，拼车的选择概率为0。而在收费机制下，由于拼车的出行成本低于不拼车，即min{pa,pp}=pp总成立，因此不拼车的广义出行成本随着后悔水平参数λ的增加而增加，而拼车的广义出行成本则不变，如图3(d)所示。

5 结束语

本文在瓶颈模型的基础上，采用基于后悔理论的Logit模型刻画出行者在两种出行模式—单独驾车出行和拼车出行之间的决策行为，并分别考虑了不收费和最优收费两种机制下出行者的出行时间及出行选择。研究表明，在不收费机制下，单独驾车出行者和拼车出行者混合出行；而在最优收费机制下，则实现了交通流的分离。其中，拼车出行者在瓶颈的高峰出行，而单独驾车出行者则在瓶颈的颈部出行。此外，该模型引入的后悔厌恶水平刻画了人们不同的后悔程度，将行为科学的后悔理论应用到出行模式选择建模中，提高了理论对现实出行模式选择行为的解释能力。算例结果验证了后悔厌恶程度对出行模式选择行为的影响。