基于Expectile和Realized GARCH模型的波动率预测
高雷阜, 李伟梅
(辽宁工程技术大学 运筹与优化研究院,辽宁 阜新 123000)
0 引言
收集、分析风险相关信息,进行风险评估,然后制定、实施相应的对策,使风险被控制在所能接受的范围内,这是金融风险管理的主要内容。其中,风险评估在风险管理中扮演着重要的角色,而风险预测对风险评估的准确性有重大影响。因此,在当代经济复杂的环境下,如何精确预测风险是风险管理中不可或缺的研究内容。
波动率是评估风险的核心方法之一。在金融时间序列早期的相关研究中,研究者发现风险预测误差与金融市场的波动相关。1982年Engle[1]提出的条件异方差模型(ARCH模型)刻画了这种相关性,但ARCH模型待估计的参数繁多不利于快速计算。为了修正ARCH模型,Bollerslev[2]提出的GARCH模型被称为广义ARCH模型,克服了ARCH模型的不足。自此之后,GARCH模型被广大研究者推广并提出很多改进模型,如TGARCH模型、EGARCH模型等,但这些模型多建立在低频数据上,预测的波动率精确度有限。随着科技的发展,高频数据逐渐走进风险预测研究领域。Andersen[3]等人基于高频数据,提出已实现方差RV,证实了RV更加接近实际风险波动。2012年Hasen[4]将RV与GARCH模型结合提出了Realized GARCH模型(下文简称RGARCH),进一步提高了波动率预测效能。与此同时,其他研究者相继将已实现波动率用于各种GARCH衍生模型。其中,王天一和黄卓[5]研究了高频数据下波动率的建模及应用。GARCH及GARCH衍生模型对波动率的预测都需要假设模型分布,但是满足模型条件的分布很难找到。分位数回归的GARCH模型不需要假定模型分布,将分位数回归引入波动率预测模型[6,7],可缓解分布假设造成的模型误差,但分位数无法准确捕捉分布尾部信息。Expectile(期望分位数)由Newey Powell[8]提出,和分位数具有一一对应的关系,Expectile比分位数对分布的尾部信息更加敏感[9,10,11]。将Expectile和高频数据引进GARCH模型是否会碰撞出更精彩的波动率预测结果目前还未有研究。
本文基于分位数回归GARCH模型的思想及Expectile、高频数据的良好性质,提出Expectile-RealizedGARCH(简称E-RGARCH)模型,旨在提高波动率预测能力,使得风险预测更加准确。
1 模型
1.1 RGARCH(1,1)模型[12]
(1)

1.2 E-RGARCH(1,1)模型
(2)
其中,
(3)
为非对称平方损失函数。τ为[11]
(4)
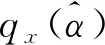
在RGARCH(1,1)模型的基础上引入Expectile得到E-RGARCH(1,1)模型
(5)
其中,ωτ,ατ,βτ,λτ,δτ分别为ω,α,β,λ,δ的第τ个Expectile值。
2 模型估计
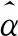
(6)
3 条件波动率预测与评价
3.1 样本外动态波动率滚动预测
采用固定时间窗口宽度的样本外1步滚动预测法[13]对不同模型的条件波动率进行预测。具体方法为:将样本数据分为M个样本内和N个样本外,样本内用于参数估计,样本外用于预测。当一个新的观测值增加到样本中,删除第一个观测值并重新估计模型,得到一个新的波动率预测值,重复进行N次,得到N个样本外波动率预测结果。
根据均方差(MSE)[14]
(7)
评价模型预测能力。其中,ht为第个条件波动率预测值,RVt为第t个已实现波动率。MSE值越小,代表预测能力越好。
4 实证研究

图1中日收益率Rt表现出尖峰厚尾特征,图2中已实现波动率RV具有波动聚集性。
4.1 数据预处理
分析日收益率Rt的数据特征,判断能否应用RGARCH模型对其进行预测。
4.1.1 描述性统计量
分析日收益率的描述性统计特征,结果如表1所示

表1 日收益率描述性统计量
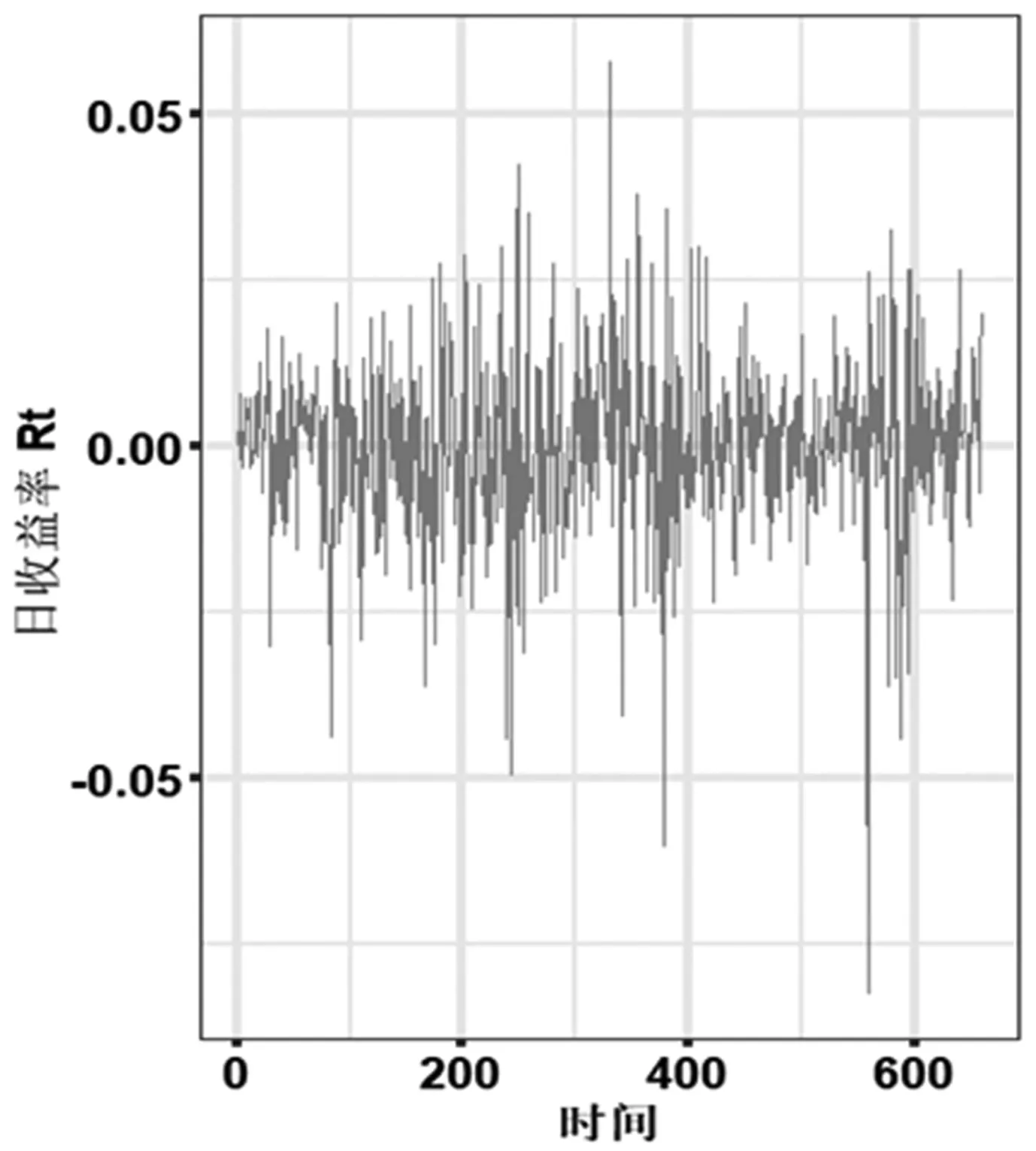
图1 日收益率Rt时间序列图
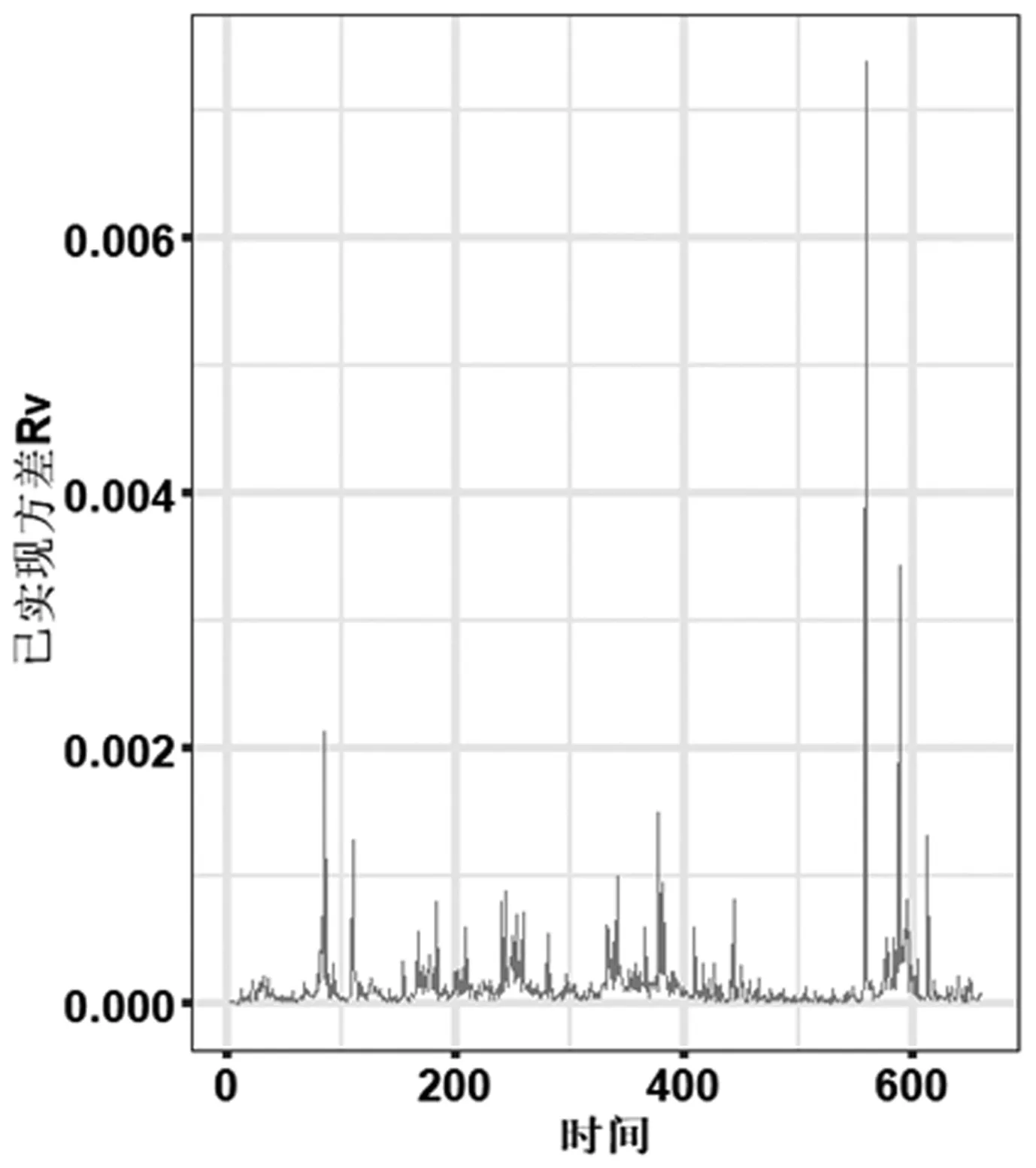
图2 已实现波动率RV时间序列图
表1中日收益率具有向0集中的趋势,收益率分布不分散。偏度系数结果表示分布偏左。样本峰度说明分布具有高峰厚尾。JB检验统计量P值小于0.05,说明不服从正态分布。ADF检验结果说明Rt为平稳序列。
4.1.2 自相关性检验
应用自相关ACF和偏自相关PACF可对日收益率Rt进行相关性分析,结果见图3。
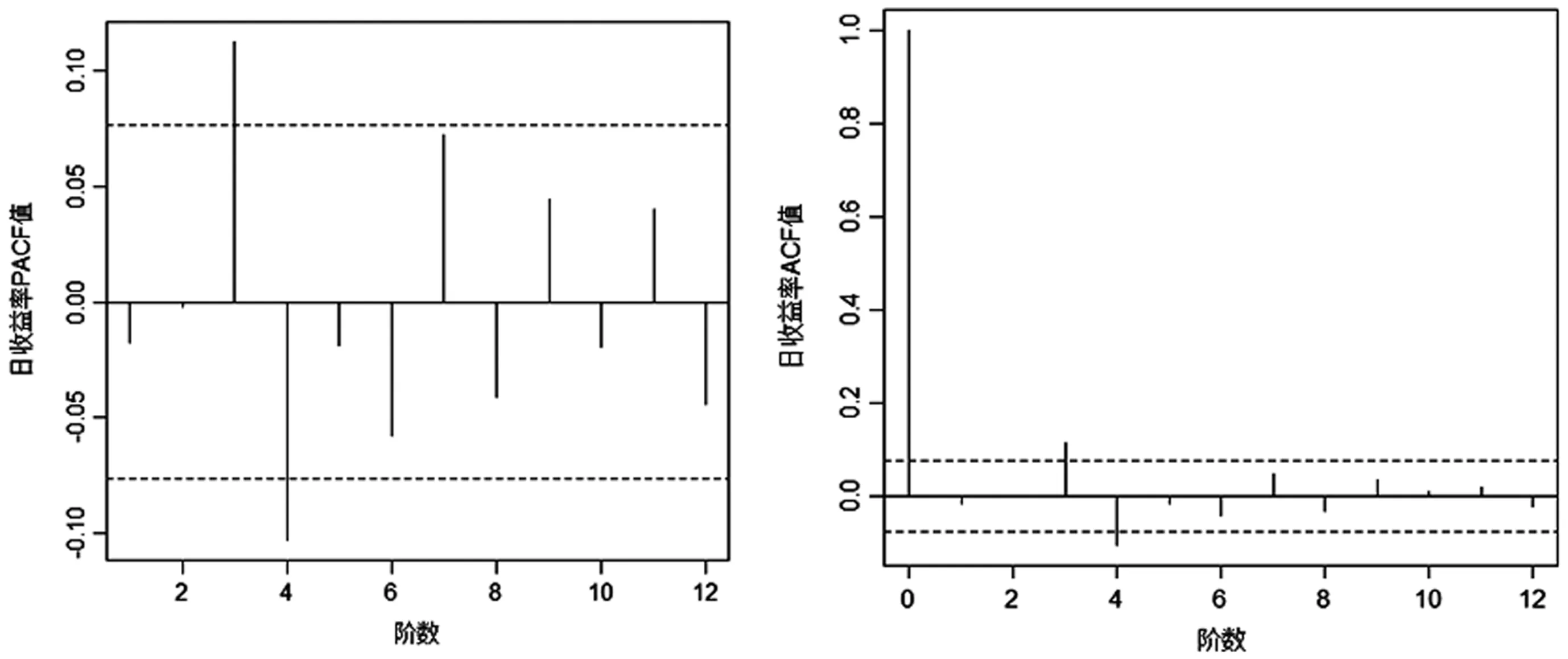
图3 日收益率Rt的ACF和PACF检验
根据图3,ACF和PACF函数值基本在置信区间内(图中虚线区域内),说明日收益率Rt自相关性较弱。
Box-Ljung检验[16,17]是对时间序列是否存在滞后相关的一种统计检验,检验日收益率Rt滞后相关性,若不相关,则为白噪声序列。

表2 日收益率Rt的Box-Ljung检验
根据表2,滞后阶为12时P值大于5%,日收益率Rt为白噪声序列。
结合图3和表2,我们认为沪深300指数的日收益率Rt不存在显著高阶自相关性,可以应用RGARCH(1,1)模型对其分析研究。
4.2 模型建立
4.2.1 均值模型的建立

(8)
在的RGARCH(1,1)模型引入Expectile,得到相应的E-RGARCH(1,1)模型为
(9)
4.2.2 模型参数估计
选取前559个交易日的日收益率Rt作为样本内数据估计模型参数,得到的结果如表3和表4所示。
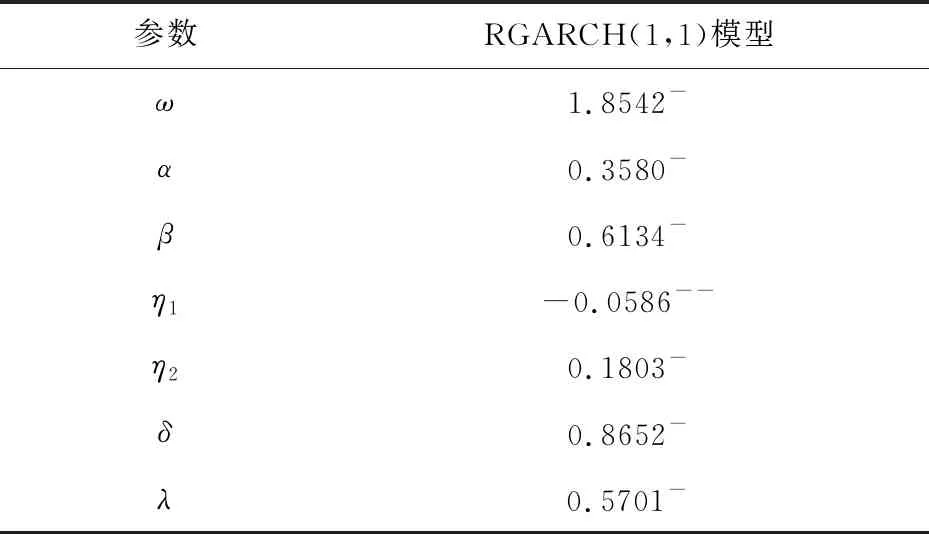
表3 RGARCH(1,1)模型参数估计结果

表4 E-RGARCH(1,1)模型参数估计结果
4.2.3 条件波动率预测和评价
在以上参数估计基础上,将2017年10月13日至2020年2月3日的559个数据视作样本内数据,2020年2月4日至2020年7月1日的100个数据视作样本外数据,对RGARCH(1,1)模型和E-RGARCH(1,1)模型的条件波动率进行预测,其预测结果与样本外已实现方差的对比如图4所示。
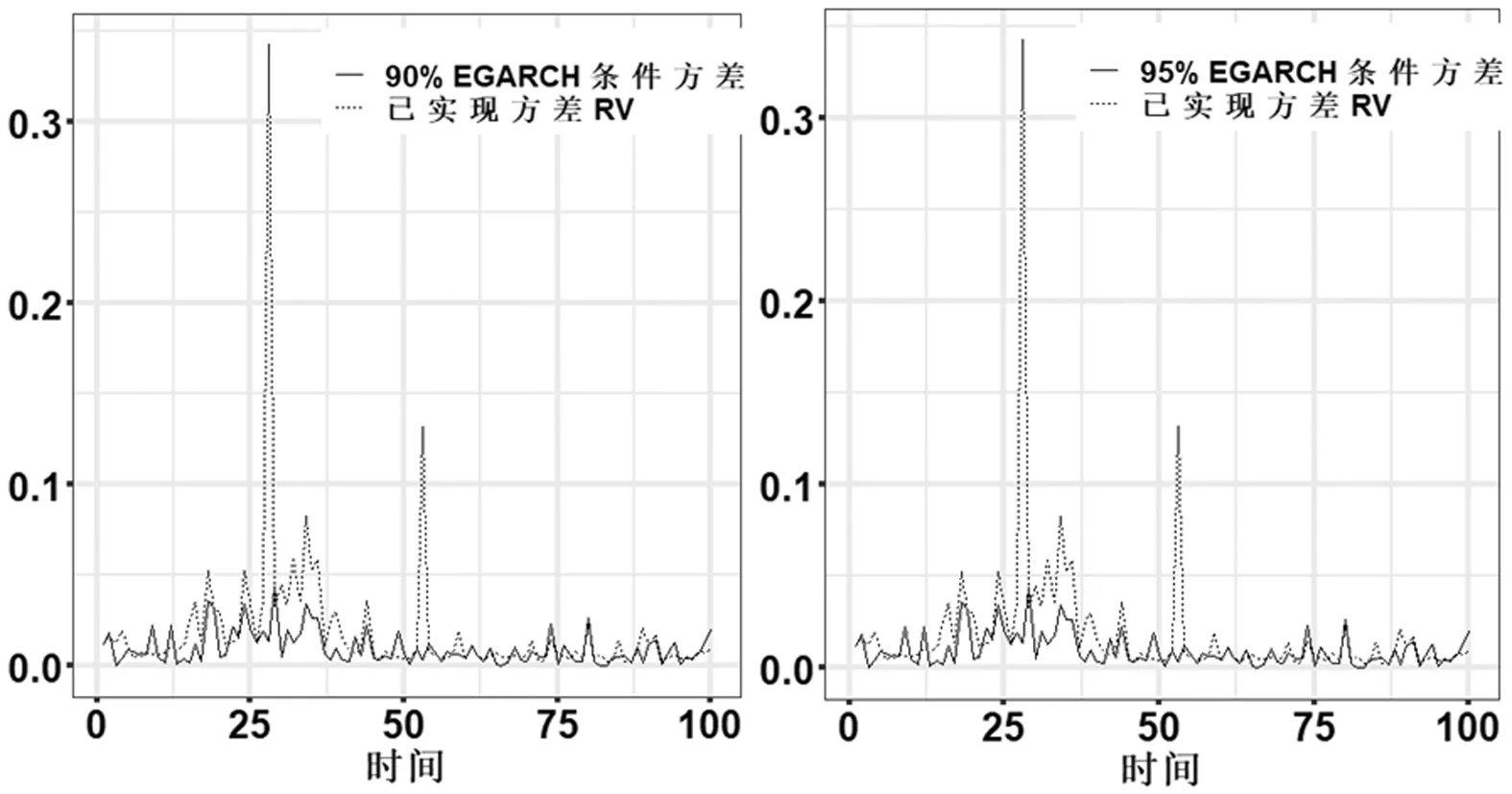
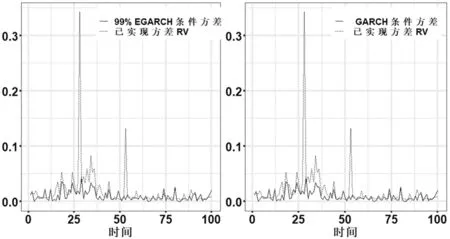
图4 RGARCH(1,1)模型和不同风险水平下的 E-RGARCH(1,1)模型条件波动率预测图
图4中RGARCH(1,1)模型和E-RGARCH(1,1)模型对条件波动率预测都有较好的效果,以下应用均方差(MSE)对预测效能作进一步评价,结果如表5所示。
根据表5结果,E-RGARCH(1,1)模型波动率预测能力均比RGARCH(1,1)模型好,当风险水平为0.95时,E-RGARCH(1,1)的波动率预测能力最好。
5 结论
基于高频数据的E-RGARCH模型较传统的RGARCH模型对波动率预测更加准确的,这对金融市场风险管理有一定的指导意义。本文采用极大似然法估计模型参数,并没有考虑参数的约束信息,而贝叶斯估计法假定了参数的先验分布,使得参数估计效果更佳。因此,基于贝叶斯估计的E-RGARCH模型可作为未来研究方向。

