基于R/S和Morlet小波分析的北洛河上游径流变化特征
谢智博, 穆兴民,2, 高 鹏,, 邱德勋
(1.西北农林科技大学 水土保持研究所 黄土高原土壤侵蚀与旱地农业国家重点实验室,陕西 杨凌 712100; 2.中国科学院 水利部 水土保持研究所, 陕西 杨凌 712100; 3.中国科学院大学, 北京 100049)
径流量是流域气候及下垫面综合作用的结果,同时是流域水资源分配的重要依据,其变化通常可以使水资源供需关系发生改变从而导致旱涝灾害的发生。黄土高原地区气候暖干化以及大范围退耕还林(草)等生态修复工程的实施导致黄河干流及其支流的径流量发生了显著的变化,进而对流域生态环境和社会经济可持续发展造成一定的威胁[1-3]。目前,国内众多学者对于径流变化已经做了大量研究。如李二辉等[4]通过分析黄河干流陕县站和河口镇站径流量演变过程,得到自1985年以来,黄河上、中游年径流量呈不断减小趋势,径流变化具有明显的阶段性,经历了枯—丰—枯3个时期。在渭河流域径流年际变化方面,黄晨璐等[5]依据渭河1956—2016年实测径流资料,得到渭河径流量呈显著减少趋势,且分别在1970年和1994年发生突变。对于径流量减少的原因,张丽梅[6]、Zhao[7]等对渭河流域多年实测径流数据进行了系统分析,指出剧烈的人类活动所引起的下垫面变化是径流量减少的主要因素,而且在不同水土保持措施的实施阶段,其对径流变化的影响程度要远远大于气候变化(如降水变化和潜在蒸散发)。针对渭河流域径流量未来的变化趋势,王小杰等[8]研究表明,渭河流域径流量未来变化趋势与历史演变规律具有正相关性,即渭河干流径流将呈持续下降趋势。北洛河是黄河中下游多砂粗砂区和暴雨洪水等自然灾害的主要源头,其水文水资源的变化同样引起了学者们的广泛关注。如晁智龙[9]和董其广等[10]以实测水文数据为基础,分析了北洛河流域径流的变化,得出志丹、吴旗、刘家河以及交口的年径流量均表现为极显著减少趋势,而且在20世纪60,70年代,其径流量在年内分配比较集中,丰水期和枯水期径流量变化趋势与全年基本保持一致。随着近几年北洛河上游年径流量持续偏枯,研究其径流变化趋势和分配特征及周期性变化规律则具有一定的现实意义。
本文基于北洛河上游吴旗水文站1971—2014年逐月径流量数据,采用M-K(Mann-Kendall)趋势分析法和R/S法(rescaled range analysis)分析汛期和全年径流量的变化趋势及其变化连续性,同时采用Morlet小波变换分析径流量年周期特征,以期为该流域生态环境建设以及可持续发展提供理论参考。
1 研究区概况
北洛河是渭河的一级支流,黄河二级支流。本文中北洛河上游指的是吴旗水文站以上流域(107°32′39″—108°32′45″E,36°44′57″—37°19′30″N)。流域面积为3 408 km2,河长275.6 km,吴旗水文站位于36.9°N,108.2°E,海拔1 331.4 m。地貌类型属于黄土高原丘陵沟壑区,地势总体为西北高,东南低。研究区所属气候为温带大陆性季风气候,春季干旱多风,温差较大,夏季闷热,秋季霜冻期较早,冬季风多雪少。流域内主要土壤类型为黄绵土,年均气温7.7℃,无霜期96~145 d,多年平均降雨量454.9 mm,降水量年内分配不均,主要集中在7—9月,且多以暴雨形式出现[11-13]。
2 数据来源与研究方法
2.1 数据来源
根据《黄河流域水文年鉴》中北洛河流域吴旗水文站1971—2014年逐日径流量资料整理计算得到月径流量和年径流量,数据序列经过严格检查,以确保其准确和可靠。
2.2 研究方法
2.2.1 Mann-Kendall趋势检验法 Mann-Kendall趋势检验法(简称M-K检验)是一种非参数统计检验方法,广泛应用于水文时间序列的分析研究。因为其能够对水文气象要素的整体变化趋势进行定量刻画,在时间序列分析上具有独特的优势,能够很大程度上减少非正常值对结果的影响,也不会受到数据分布特征的影响,可以对水文气象序列的趋势进行有效的分析研究[14-16],其统计量的计算与分析可参考文献[17—19]。
2.2.2 R/S分析法 R/S分析法是一种识别时间序列长程相关(反相关)持续性(反持续性)的简单而又有效的方法,能够很好地运用于水文时间序列的分析,为研究时间序列长程相关性提供了理论支撑,其最大优势在于不必假定时间序列的分布特征,能够大大简化对系统的长程相关特性的分析[20-21]。根据R/S分析可以得出Hurst指数,其值大小可作为时间序列是否存在趋势性成分的依据,并表征其趋势强度[22]。对于一个非随机水文序列,首先应该满足[20,23]:
R(h)/S(h)=(ah)H
(1)
式中:R(h)/S(h)为重标极差;h为增量区间长度;a为常数;H为Hurst指数,其过程为:
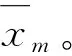
其次,计算Dm(h个期间)的累积离差Xk,m:
(2)
接着用Xk,m来算Dm极差Rm以及其准差值Sm,根据以上公式结果来计算Dm的重标极差。
(R/S)m=Rm/Sm
(3)
对于每一个子序列都需要重复以上步骤,那么可以得到整个序列的重标极差.
(4)
不断增大h,直到满足h=N/3,最终可以得到{x(t)}的重标极差系列,并且满足公式(1),对公式(1)两边取对数可得:
lg(R/S)h=Hlga+Hlgh
(5)
解释变量为lgh,被解释变量为lg(R/S),以此来作散点图,用最小二乘来拟合直线,直线斜率就是Hurst指数。
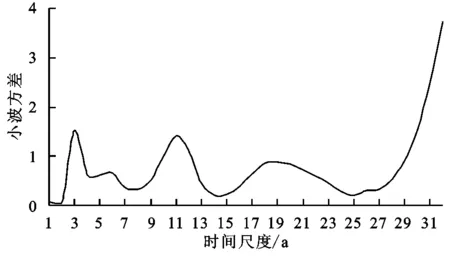
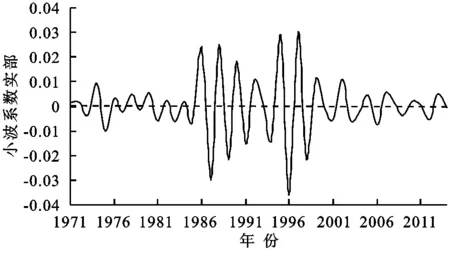
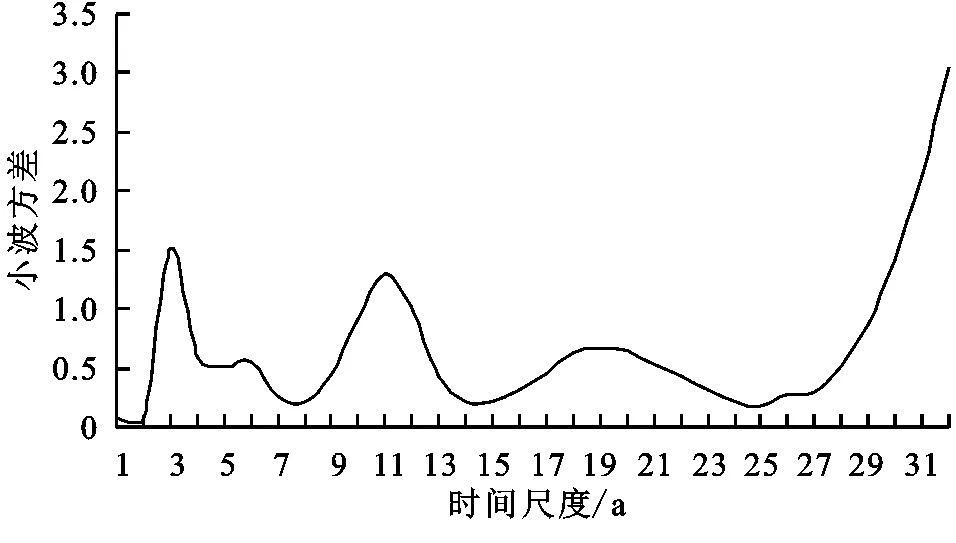
该方法判断规则:若0 2.2.3 小波分析法 小波分析(wavelet analysis)在分析水文时间序列方面具有强大的分辨多尺度的功能,而且在时域和频域上具有良好的局部化功能,能识别出水文序列或高或低不同的频率成分和不同时间尺度的主要变化周期,从而对未来发展趋势做出准确预测[17,24]。本文所用的Morlet小波定义如下[25]: (6) 式中:Wf(m,n)为小波变换系数;m为尺度因子,代表小波的周期尺度;n为时间因子,代表时间上的平移。 Wf(m,n)能同时反映参数m和n的特征,并随着二者变化而变化。用n当横坐标,m当纵坐标来绘制关于Wf(m,n)的小波变换系数图,根据图中二维等值线闭合中心的正负值和小波系数的零点来判断径流的增减性和突变性。以不同时间尺度m为横坐标,以各尺度下的小波方差为纵坐标绘制小波方差图,径流序列的主要变化周期可参照图中各个峰值来确定[26]。 本文使用Matlab软件的Complex Continuous Wavelet工具箱计算得到北洛河上游吴旗站1971—2014年年径流量和汛期径流量的小波系数后,用Surfer 16软件绘制小波变换实部分布图和小波系数模等值线图,用Excel 2019绘制小波方差图和第一主周期时间尺度小波系数实部过程线图。小波变换实部分布图能够反映径流量在不同振荡周期尺度下的周期性变化;小波系数模等值线图能够反映不同振荡周期尺度下周期性的强弱,其模越大,周期性特征就越明显;小波方差图反映不同振荡周期尺度下波动能量的分布情况,峰值用来确定径流量的变化主周期[27]。 从图1可以看出,北洛河上游径流主要集中在6—9月,峰值一般出现在8月。1971—2014年各年代径流量的年内分配过程呈现出基本一致的特点,为“双峰型”,峰值分别出现在3月和8月,形成春汛和夏汛,且峰值在20世纪70—80年代以及20世纪90年代—21世纪20年代均呈现降低趋势。从全年变化趋势来看,1—3月径流略微增加,主要原因是冰雪融水和春季降水较多,同时由于温度较低,蒸发较弱,所以比较容易产生径流;3—5月径流略微下降,说明随着温度升高,蒸发随之变大,导致春旱严重;6—8月径流显著增加,主要原因是夏季降水充沛,雨量大且历时短,地表起伏不平,容易形成地表径流。 图1 吴旗水文站不同年代径流量年内分配曲线 由表1可以看出,径流量最大极值比出现在90年代,而最小的极值比则出现在2011—2014年,在整个44 a内,极值比有减小的趋势,说明北洛河上游年内分配的相对变化幅度有减小的趋势。北洛河上游不同年代年内分配变差系数为0.48~1.09,变化幅度较大。20世纪90年代变差系数和完全调节系数均大于多年平均值且为最大值,表明该时期内月径流序列间的差异极大,径流年内分配状况十分不均,可能与这一时期极端天气导致的多场暴雨有关,尤其是发生于1994年8月的百年一遇特大暴雨,吴旗水文站产生的径流量是其多年平均径流量的1.3倍。2001—2014年,偏态系数越来越小,说明北洛河上游年内径流分配逐渐趋于对称。整体上,北洛河上游径流年内分配变差系数与完全调节系数以及偏态系数之间的变化规律呈现出一致性:1971—2014年,三者数值大体呈不断减小趋势,年内月径流相对月均值的偏斜程度不断减小,年内分配不均匀性逐渐变小,说明随着时间的推移,径流量年内分配不均匀状况有所缓解,即北洛河上游径流量年内分配逐渐趋于均匀化。 表1 吴旗水文站不同年代径流量年内分配特征值参数 北洛河上游全年、汛期的年际径流量序列变化趋势具有较高的一致性(图2),具体表现为两个径流量序列有着相似的“峰值”和“谷值”特性,并呈现出逐渐减小的趋势。其中,全年径流量序列与汛期径流量序列峰值出现的时间基本相同,以1975年和1981年为例,汛期和全年径流量序列均各出现一个峰值。两个径流量序列的最大值分别为汛期1.36亿m3(1994年)、全年1.62亿m3(1994年),最小值分别为汛期0.20亿m3(2001年)、全年0.42亿m3(2008年、2012年)。根据径流量序列线性回归方程可知:全年和汛期的径流量减少速率较为接近,全年径流量平均每10 a减少0.134亿m3,汛期径流量则平均每10 a减少0.115亿m3。由于汛期径流量在年径流量中占有较大比重,因此两个径流量序列减少速率相近。径流量减少一方面是因为气候变化,另一方面是因为人类活动的加剧引起流域下垫面发生变化,且后者对径流量变化的影响程度要远大于前者[6]。为了进一步反映北洛河上游径流变化趋势特性,采用M-K趋势检验法和R/S分析法对两个径流量序列变化趋势的显著性和持续性进行分析,结果见表2。两个径流序列M-K检验值和线性拟合结果较为一致,得到的统计量Z值均小于0且数值远远超出临界值-2.58,表明径流量序列变化趋势均在0.01置信水平上显著减少。根据R/S分析得出汛期径流量和全年径流量Hurst指数为分别为0.69,0.53,均介于0.5~1,表明两个径流量序列均存在一定的长期记忆性,即递减趋势在未来都具有一定的持续性,但全年径流量持续性的可能性要小于汛期径流量序列。 图2 吴旗水文站各径流量序列线性趋势 表2 吴旗水文站各径流量序列趋势特征 根据多年径流量小波分析结果(图3),同一时间尺度下,小波系数正值等值线代表丰水期,负值等值线代表枯水期,零值等值线则代表平水期。在44 a时间序列中,年径流量存在2~5 a,16~27 a两种时间尺度的枯—丰变化振荡周期和8~14 a时间尺度的丰—枯变化振荡周期,其中8~14 a丰—枯变化震荡周期和16~27 a枯—丰变化振荡周期最为显著。8~14 a周期性变化具有全域性,共经历了丰—枯—丰—枯—丰—枯—丰—枯—丰—枯—丰—枯12个交替变化,具体丰水时段为1971—1972年、1977—1980年、1984—1987年、1992—1994年、2000—2002年、2006—2009年、2013—2014年,且2014年后实部正值等值线未闭合,说明丰水期在2014年后还会持续一段时间。16~27 a尺度上,全年径流也存在丰枯振荡,经历了枯—丰—枯—丰—枯—丰—枯—丰8个交替变化,但比较紊乱。在2~5 a尺度上,周期性最强(图4),在时域上分布也比较明显,主要发生在1971—2000年,振荡中心在1994年左右;10~14 a和16~24 a尺度上周期性也比较强,其中10~14 a尺度具有全域性,16~24 a主要发生在1971—1994年,振荡中心在1971—1973年以及1975年左右;其他时间尺度上周期性则相对较弱。 从图5可以看出,3个较为明显的峰值,可以看出年径流存在3,11,19 a的周期变化特征。其中3 a时间尺度对应最大峰值,所以3 a的时间尺度对应的周期变化最强烈,是其年径流变化的第一主周期。11 a和19 a时间尺度分别对应第二主周期和第三主周期。将小波方差分析与小波实部时频变化相结合,可以推测出年径流3个主周期变化规律相互对应,并且3个主周期均和其时间尺度中心相重合。其中,在3 a时间尺度上,径流的平均振荡周期为1.5 a左右,1971—2014年大约经历了19个丰水期和18个枯水期,可以作为水文周期预报的参考性周期,同时根据径流的丰枯周期,可以适当调整工业、农业用水,保证城市生活供水情况(图6)。另外,年径流序列还可能存在更长时间尺度的变化周期,但这需要更长的径流序列来进一步验证。 图5 年径流量小波系数方差 图6 年径流量3 a时间尺度的小波系数实部过程线 汛期径流量序列与年径流存在相似的丰—枯交替变化周期,其所经历的丰枯变化过程也极为相似,且包含的主周期相同(图7),即均包含3,11,19 a共3个变化主周期,推测可能和汛期径流量在全年径流量中占有较大比重有关。已有研究表明:西北地区旱涝存在9 a和2~3 a的短准周期振荡[28],而且本文得出的结论在有关降水量的周期性研究中与主汛期降水与年降水的周期变化较接近的结论相一致[29],由此可以说明北洛河流域年径流量与西北地区气候的变化周期基本一致。 图7 汛期径流量小波系数方差 (1) 北洛河上游年内径流量主要集中分布在6—9月,占全年径流的70%以上,最大径流量一般出现在8月,径流量年内分配曲线呈“双峰型”。2000年以前,径流量年内分配不均匀程度较大,2000年之后,年内分配不均匀程度相对较小且逐渐减弱。 (2) 1971—2014年北洛河上游全年、汛期两个径流量序列的变化均呈显著减少趋势,其减少过程在未来均存在一定的持续性。 (3) 北洛河上游径流量存在丰—枯交替的多尺度变化特征和多主周期变化规律。年径流量和汛期径流量序列呈现出相似的变化周期,其3个主周期依次为3,11,19 a左右。其中,当时间尺度为3 a时,径流量的平均振荡周期为1.5 a左右。3 结果与分析
3.1 径流量年内变化
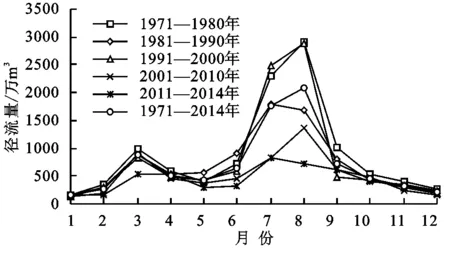
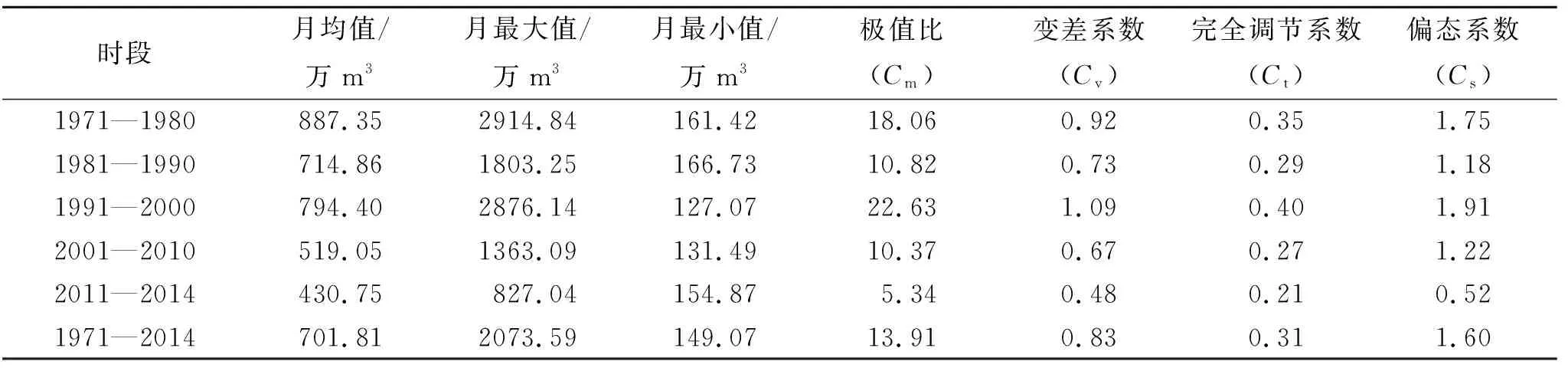
3.2 径流量年际变化
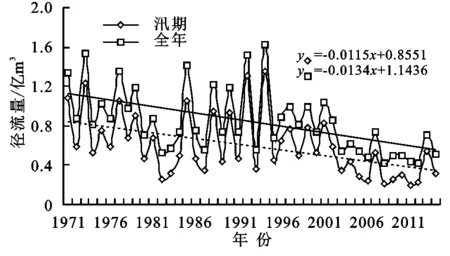

3.3 径流量周期特征分析
4 结 论

